このページでは「速さが変化する運動」「速さが変化しない運動」「等速直線運動」について解説しています。
動画による解説は↓↓↓
チャンネル登録はこちらから↓↓↓
1.速さが変化する運動
今、あなたは自転車でゆっくり進んでいます。
もっと速く走りたいなあと思ったらどうしますか?
ペダルに力を思いっきり加えますよね。
スピード出し過ぎたと思ったらどうしますか?
ブレーキをかけてタイヤの動きを止めるように力を加えますよね。
このように力がはたらくと物体の速さは変化します。
次のような例を見てみましょう。
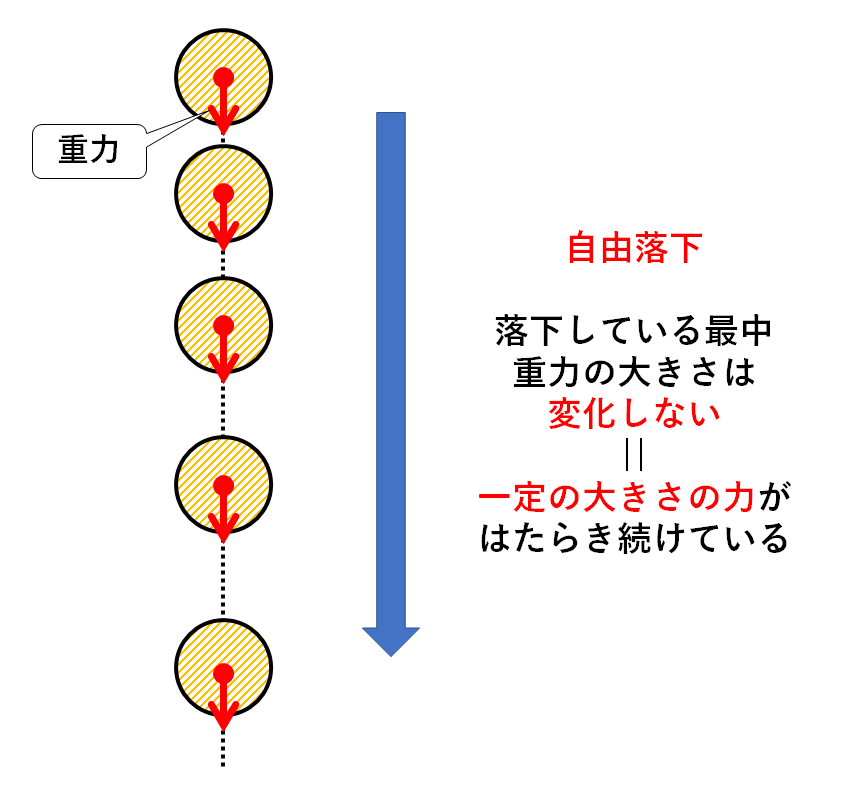
今、手でにぎっているボールがあって、自然に手をはなします。
そうすると物体は落下します。
それは重力という力がはたらくからですよね。
重力の大きさは落下中、変化しません。(↓の図)
このときボールの速さは一定の割合で増していきます。
(このように、自然に落下する運動を自由落下といいます)
ここで重要なのは
一定の大きさの力がはたらき続けている物体
→ 一定の割合で速さが変化する
ということ。
逆に
・一定の割合で速さが増加
→ 運動の向きと同じ方向に一定の大きさの力がはたらいている
・一定の割合で速さが減少
→ 運動の向きと反対方向に一定の大きさの力
ということもできます。
難しいですがここは必ず押さえておきましょう。
「速さが一定の割合で増す運動」は
・自由落下
・斜面上にある物体がすべりおりる
というのが最も多い出題パターン。
このような運動の記録テープは一定の割合で長くなります。
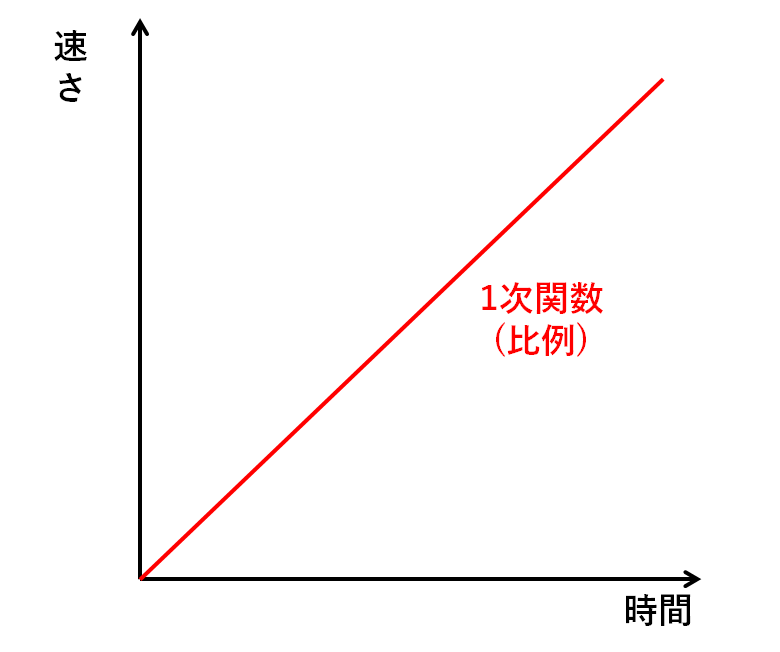
この運動について時間を横軸にとった場合の「時間と速さ」のグラフは↓の図のようになります。
「時間と移動距離」のグラフは↓の図のようになります。
2つともグラフを押さえておきましょう。
※ちなみにここで紹介した運動は「等加速度直線運動」と言います。
詳しくはこちら→【*斜面上の物体の運動】←を参考に。
POINT!!
・力がはたらくと・・・
→ 速さは変化する。
・自由落下や斜面をすべりおりる運動では・・・
→ 力が一定の大きさのまま働き続けている。
2.等速直線運動
物体が一定の速さでまっすぐ進む運動。(速さは変化しない)
「速さが変化しない」とは「物体には力がはたらいていない」ということ。
あるいは力がはたらいていたとしても、その力が別の力で打ち消されている状況。
(=つまり力がつりあっている。)
例えばスケートリンクでスケートしていることを想像してみてください。
いったん動き出せば、誰からも押されたり引っ張られたりされなくても動き続けます。
「力が加わっていない」⇒「速さが変化しない」
等速直線運動を記録したテープは↓のようにずーっと同じ長さになります。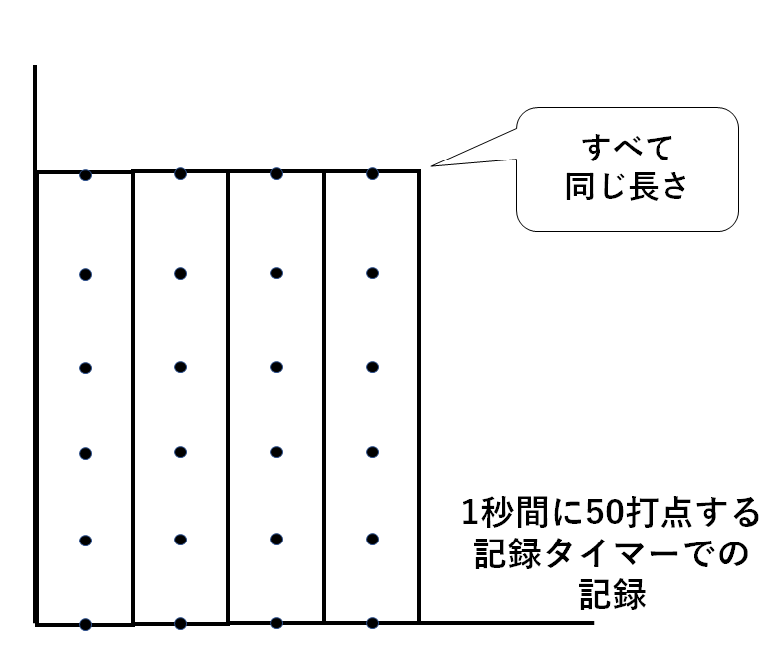
また時間を横軸にとった場合の「時間と速さ」のグラフは↓のようになります。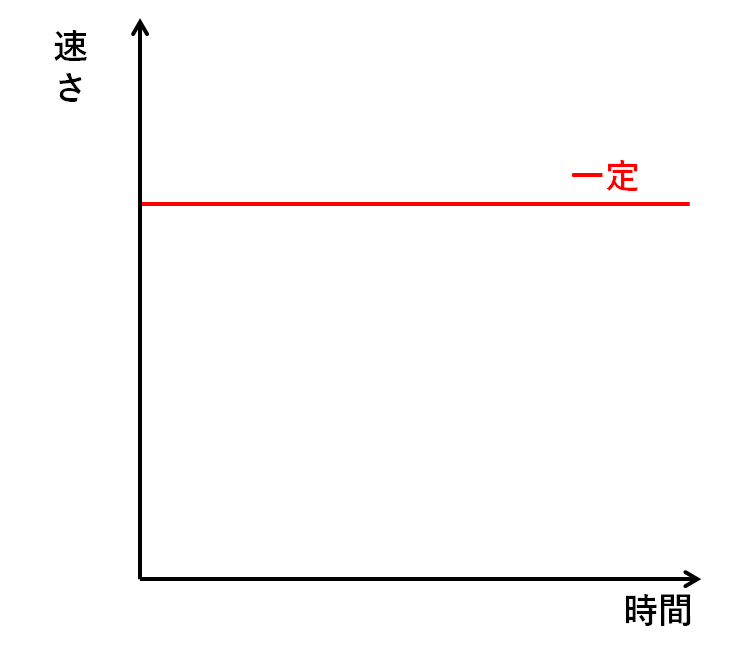
「時間と移動距離」のグラフは以下のようになります。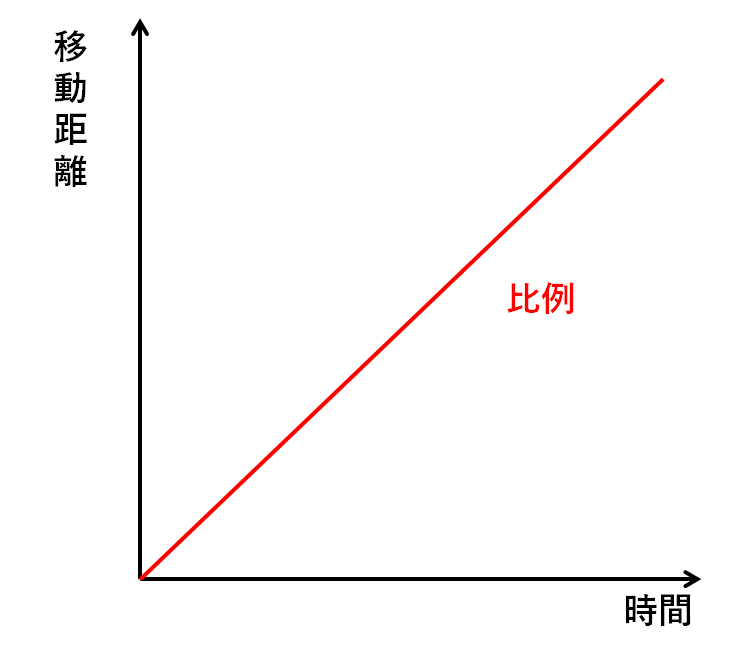
2つともグラフを押さえておきましょう。
POINT!!
・力がはたらいていない、つりあっている
→ 速さは変化しない。一定のまま。
・等速直線運動をしている物体には・・・
→ 力がはたらいていない・つりあっている。
3.慣性の法則
直前の運動の状態を保とうとするという性質のこと。
バスや電車に乗っていて急ブレーキを踏まれると、バランスを崩しちゃいますよね。
これは物体やヒトには「慣性」という性質が存在するからなんです。
慣性とは直前の運動の状態を保とうとするという性質です。
そして「物体の運動はこの慣性という性質の影響を受ける」という法則が慣性の法則です。
例その1
たとえばバスに乗っていて急ブレーキを踏まれちゃったという場合を考えてみましょう。
バスが時速60kmで走っているとします。
ということは乗客も同時に時速60kmで動いています。
そこで急ブレーキを踏むとバスの速さは減少。
しかし乗客にも「慣性=運動の状態を保とうとする性質」があります。
乗客は時速60kmで運動を続けようとしてバスの進行方向と同じ向きに倒れそうになります。
例その2
いま止まっているバスがあったとしましょう。
乗客はバスと同じく「静止」という運動をしています。
そこでバスが急発進するとどうなるでしょう。
乗客は「慣性=運動の状態を保とうとする性質」により、その場で静止し続けようとします。
つまり進行方向と反対の向きに倒れそうになるわけです。
また等速直線運動をしている物体は(外部から力を受けない限り)等速直線運動を続けます。
これも慣性の法則の例です。


コメント(承認された場合のみ表示されます)
このサイトが利用できることに本当に感謝してます
しかも無料で!
ほんと有料で提供されてても違和感ないくらいすごい完成度だと思います
マジで助かってます。本当にありがとうございます
匿名さん様
コメントありがとうございます。
恐縮ではありますが、そこまで言っていただけると私もうれしいです。
ぜひこれからもご活用ください。
中学範囲ではないのかもしれませんが
一定の力を加え続ける運動で
時間と移動距離のグラフで1/2が着くのはどうしてなんですか・・・・・・?
やまぐち様
コメントありがとうございます。
x = Vot + 1/2at^2
の式のことでしょうか?
そうです・・・・・・・・・
やまぐち様
返信が遅くなり申し訳ありません。
最初の速さがV0で、そこから一定の割合で加速している運動を考えます。
この運動のようすをグラフにすると↓のようになります。
これは一次関数なのでy=ax+bの形に表すことができて、
時間と速さの関係は 速さ=加速度×時間+最初の速さ で表すことができます。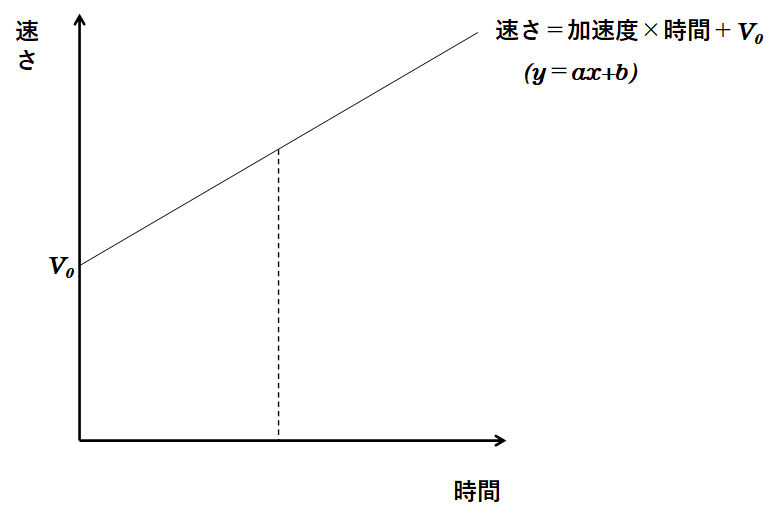
ここである時間 t秒後の速さを求めます。
数学の一次関数と同様に、時間=tを代入すると
速さ=加速度×t+V0 と表すことができます。
加速度をaとすると
速さ=at+V0 です。(↓の図)
次にt秒後までの移動距離を考えます。
横軸:時間-縦軸:速さのグラフにおいては、↓のようにt秒後までにできている図形の面積が移動距離に等しくなります。
この場合は台形です。
※なぜ面積=移動距離となるのかは、また記事を作りたいと思います。
この台形の辺の長さは↓のようになっています。
よって
移動距離=台形の面積=(V0+at+V0)×t×1/2=V0t+1/2at2
となります。
これが1/2が出てくるまでの流れですね。
これ無料でいいんですか?!ってほどわかりやすいです。学校の課題でちょうど困ってて、いいサイト見つけちゃいました。これからずっと使っていきたいです。
本当にありがとうございます。
カナカナカナナ様
コメントありがとうございます。
またいつでもご活用下さい。