中1物理【*凸レンズの写像公式】

*このページは発展的な内容を含みます。

少なくとも中3数学「図形の相似」の知識を用います。

動画による解説は↓↓↓

チャンネル登録はこちらから↓↓↓

1．写像公式

2．写像公式の証明

前項の公式の証明をしてみましょう。

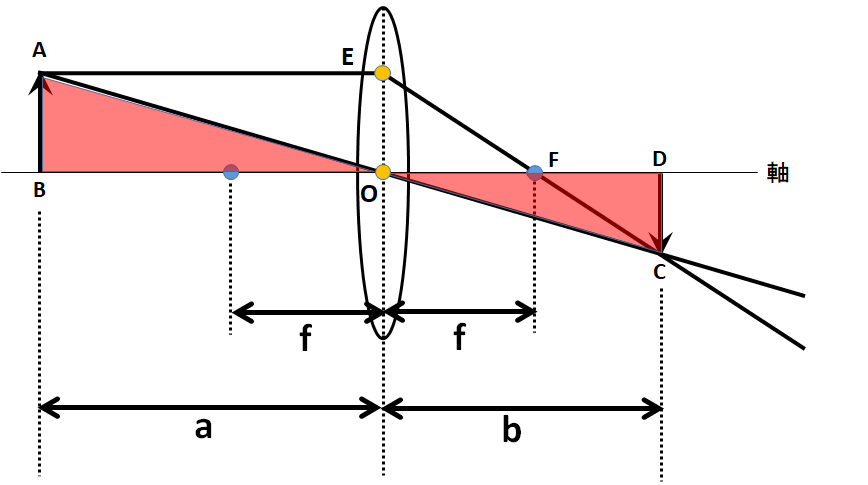
上図の中には三角形がいくつかあります。

うち下の図のような三角形を考えます。

赤い三角形どうしは相似です。(2組の角がそれぞれ等しい)

つまり△OAB∽△OCD

この相似比は

BO：DO＝a：b

よって対応する辺であるABとCDの比も

AB：CD＝a：b

となります。

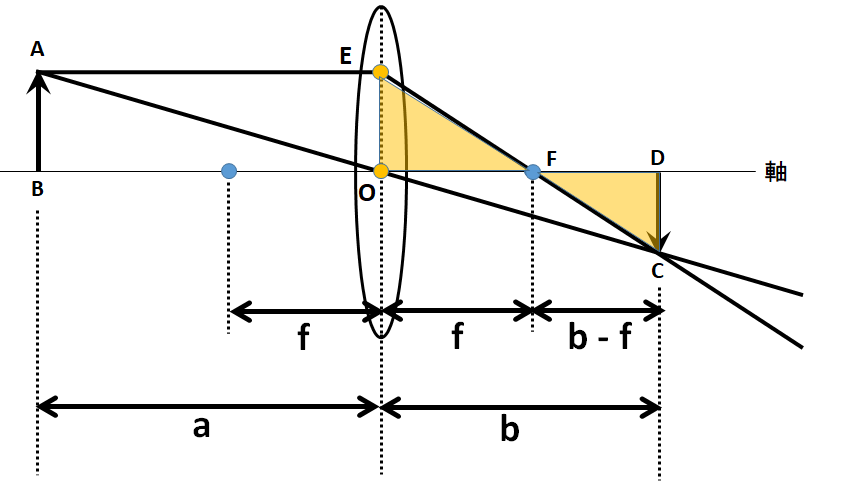
次に下図の三角形を考えます。

黄色の三角形どうしは相似です。

つまり△EOF∽△CDF

この相似比は

OF：DF＝f：b‐f

よって対応する辺であるEOとCDの比も

EO：CD＝f：b‐f

となります。

ここでEO＝ABであることに着目。

AB：CD＝a：b

EO：CD＝AB：CD＝f：b‐f

より

a：b＝f：b‐f

という式が導き出されます。

内項の積と外項の積は等しいので

$$b×f=a×(b-f)$$

$$bf=ab-af$$

両辺をabfで割ると

$$\frac{bf}{abf}=\frac{ab}{abf}-\frac{af}{abf}$$

$$\frac{1}{a}=\frac{1}{f}-\frac{1}{b}$$

よって最初に紹介した式、

$$\frac{1}{a}+\frac{1}{b}=\frac{1}{f}$$

となります。

この公式を覚えておくと便利ですが、何より重要なのは相似な三角形が隠されていることに気づくということです。

凸レンズの応用問題は相似に帰着する問題が多いです。

ヒントとして「相似に注目する」ということを覚えておきましょう。