中2物理【*ブリッジ回路その②】

このページは発展的な内容を含みます。

ブリッジ回路自体が発展的な問題ですが、その中でもさらに発展的な問題が出題されることがあります。

このページではそれを紹介しておきます。

1．ブリッジ回路のもう1つの解法

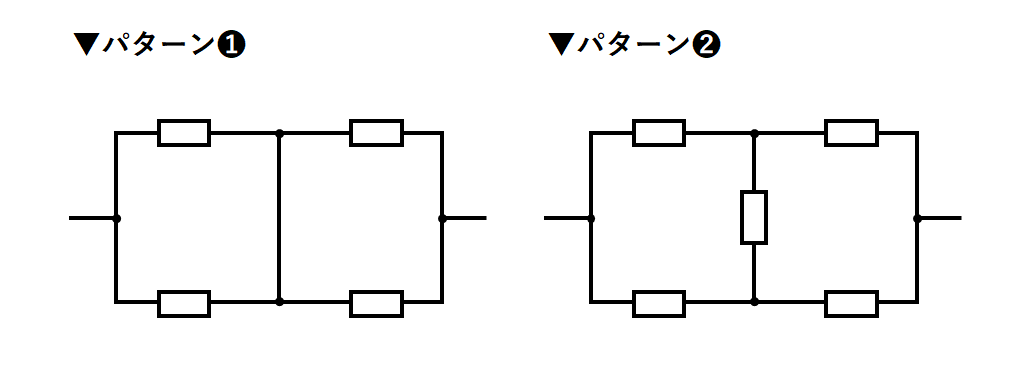
ブリッジ回路には2種類あります。

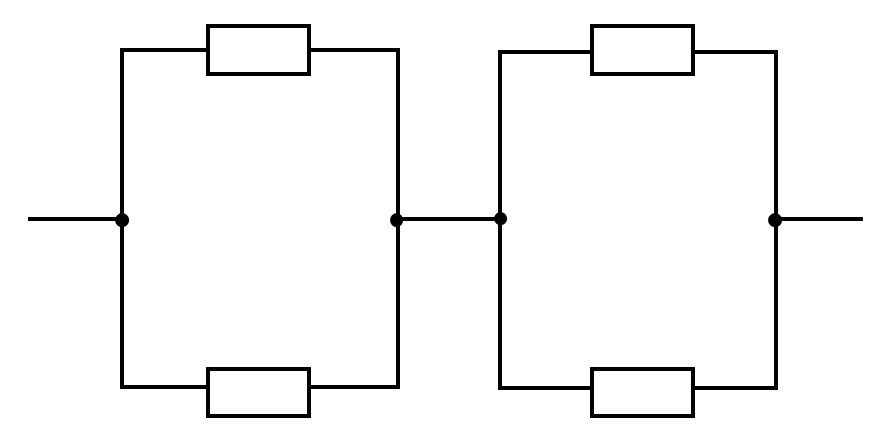
パターン❶は次のように回路を書き換えることで比較的簡単に解くことができます。

※→【ブリッジ回路】←で解説しています。

しかしパターン❷では中央の電気抵抗が邪魔で書き換えることができません。

このパターン❷の解法を見てみましょう。

例題1

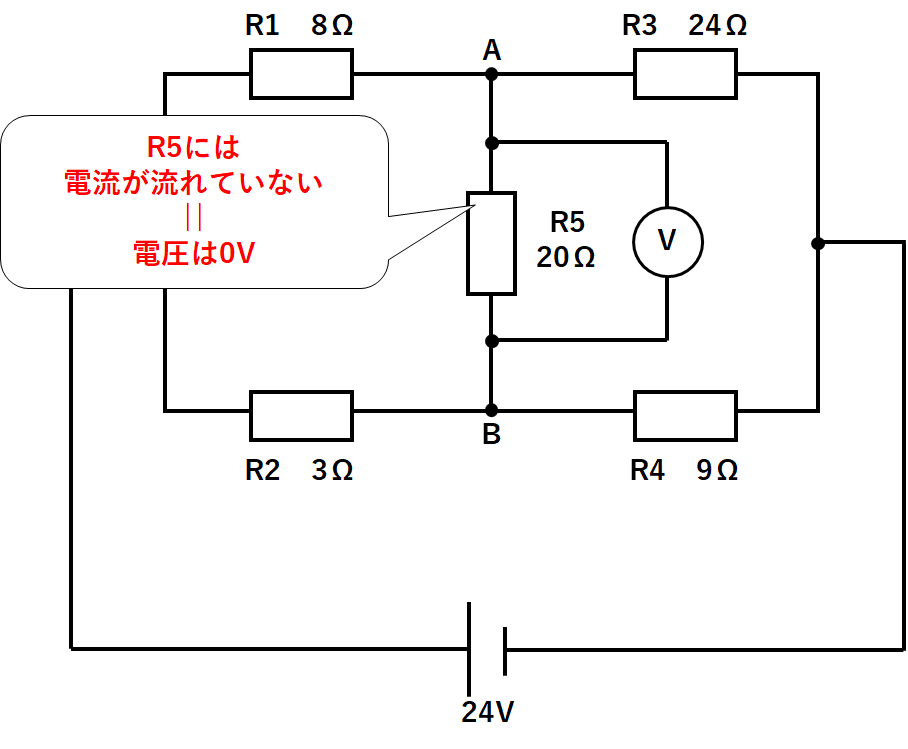
次のような回路で抵抗R5に流れる電流・加わる電圧を求めよ。

[答]
この問題の条件では →【ブリッジ回路】←で紹介した解法が使用できます。

それは

$$R1×R4=R2×R3$$

のときABの部分には電流が流れないということです。

この問題でも

$$R1×R4=8Ω×9Ω=72$$

$$R2×R3=3Ω×24Ω=72$$

となっています。[↓の図]

なのでR5には電流は流れません。[↓の図]

R5には電流が流れていないのでR5に加わる電圧も0Vです。[↓の図]

よって0A・0Vが正解となります。

例題2

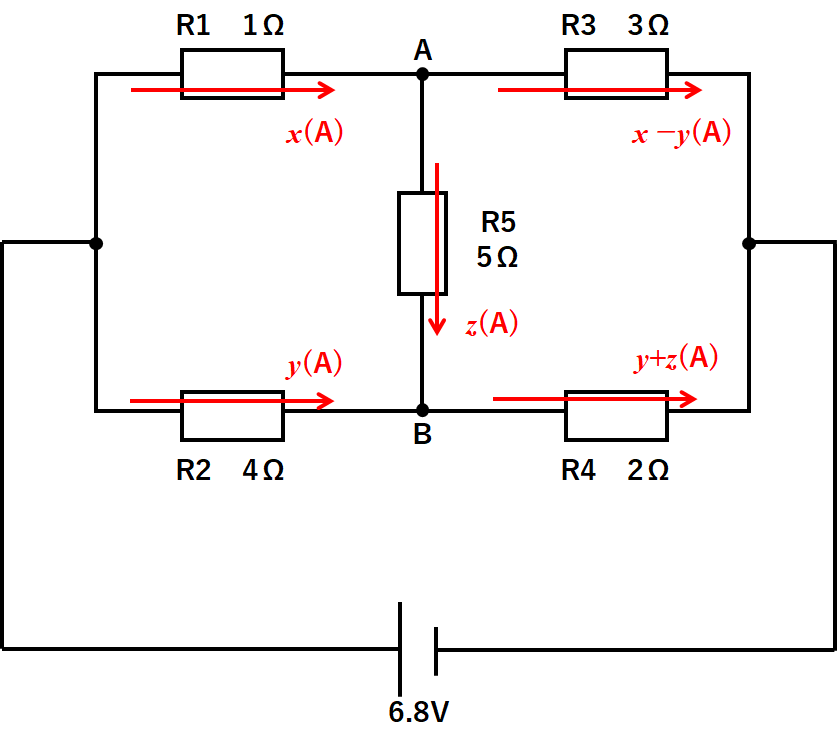
次のような回路で抵抗R5に流れる電流・加わる電圧を求めよ。

[答]
この問題の条件では

$$R1×R4=1Ω×2Ω=2$$

$$R2×R3=4Ω×3Ω=12$$

となりR1×R4・R2×R3は等しくありません。

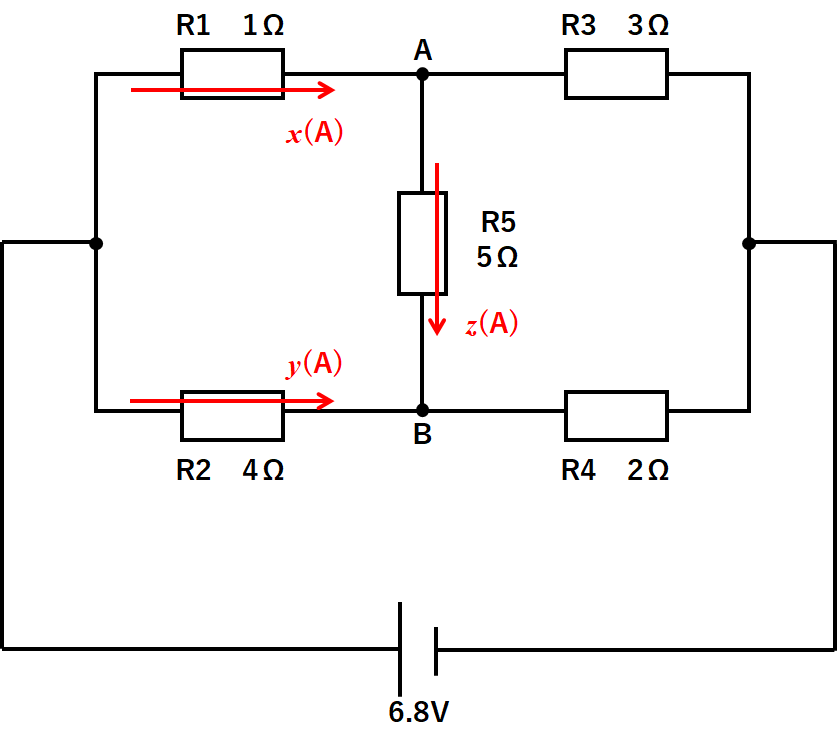
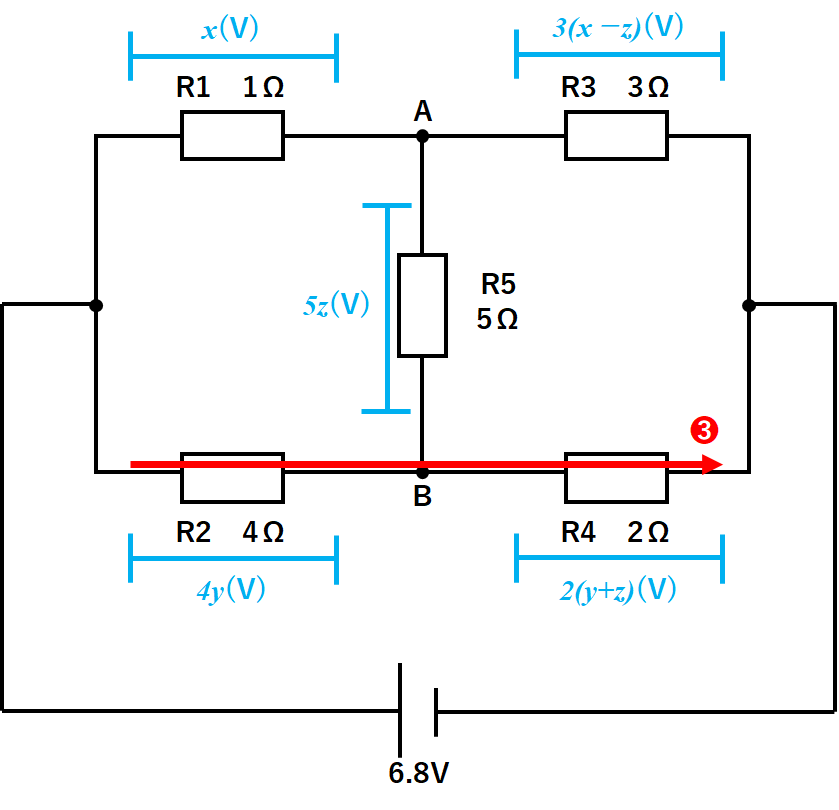
このような場合、R1・R2・R5に流れる電流をx(A)・y(A)・z(A)と文字で置きます。[↓の図]

ただしR5に流れる電流は上から下へなのか、下から上へなのかわかっていません。

よって仮に「上から下へz(A)流れているとする」と考えるのです。

計算によりzの値を求めたとき、

zの値が正である・・・上から下へ電流が流れている

zの値が負である・・・下から上へ電流が流れている

と考えるわけです。

では残りのR3・R4に流れる電流をx・y・zを用いて表しましょう。

R1を流れる電流x[A]がR3とR5に分かれるので

R3を流れる電流は

$$x-z(A)$$

と表せます。

またR2に流れる電流y(A)がR5に流れる電流z(A)と合流してR4に流れるので

R4を流れる電流は

$$y+z(A)$$

と表せます。[↓の図]

次にR1～R5に加わる電圧をx・y・zを用いて表しましょう。用いるのはオームの法則です。

$$電圧(A)＝抵抗(A)×電流(A)$$

の式を用いて

$$R1の電圧=1Ω×x(A)=x(V)$$

$$R2の電圧=4Ω×y(A)=4y(V)$$

$$R3の電圧=3Ω×(x-z)(A)=3(x-z)(V)$$

$$R4の電圧=2Ω×(y+z)(A)=2(y+z)(V)$$

$$R5の電圧=5Ω×z(A)=5z(V)$$

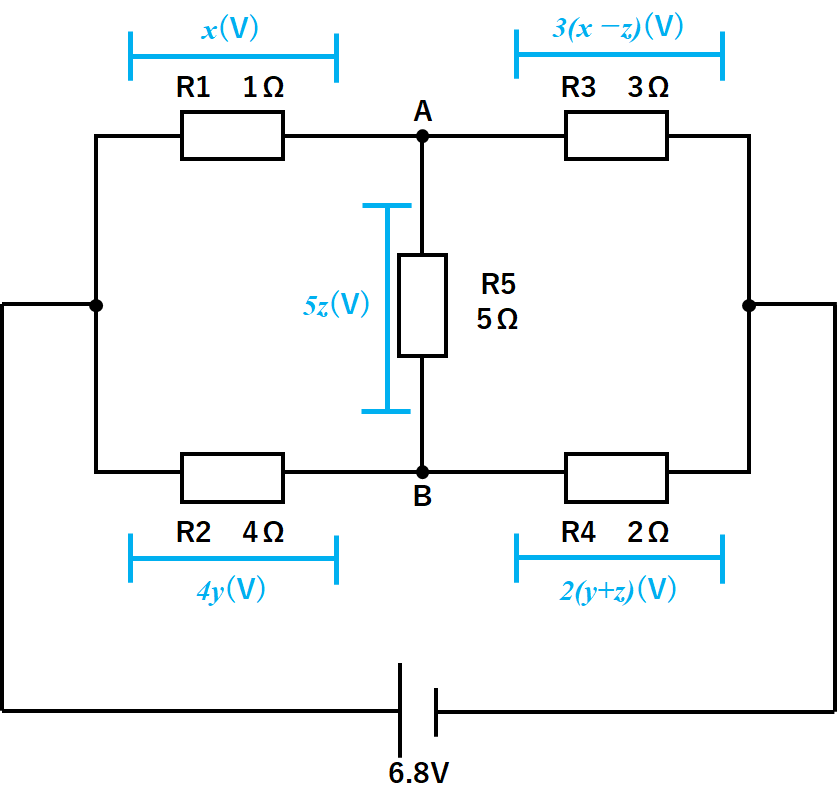
となります。(↓の図)

ここで電圧だけに注目しましょう。(↓の図)

→【電流と電圧】←のページに書いてありますが

電流は1つの道筋で電源からもらった電圧を使い切る

という法則があります。(キルヒホッフの法則と言います)

電流の通り道は3通りあります。(次の❶～❸)

電源からもらった6.8Vの電圧をこの❶～❸の道筋のそれぞれで使い切るのです。

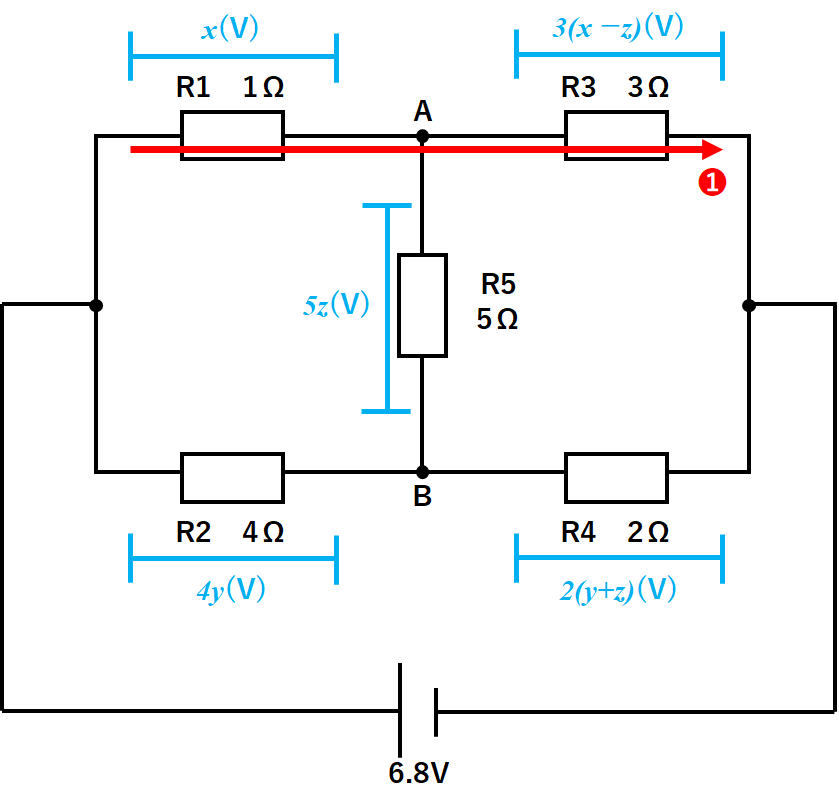
❶の場合では・・・

R1とR3で6.8Vを使い切ります。

よって

$$x(V)+3(x-z)(V)＝6.8(V)$$

という式が成り立ちます。

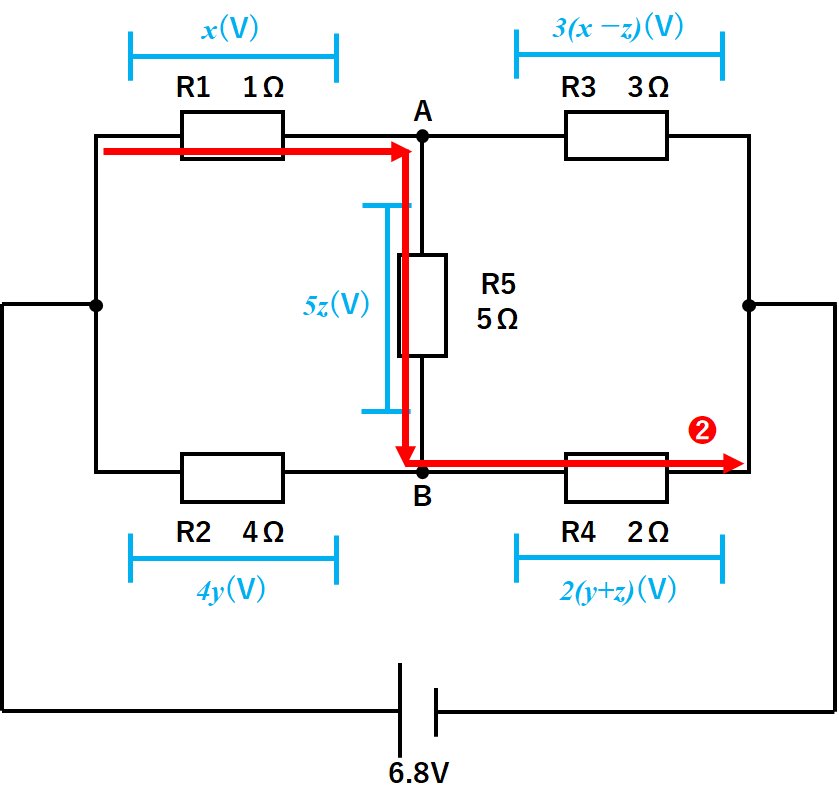
❷の場合では・・・

R1とR5とR4で6.8Vを使い切ります。

よって

$$x(V)+5z(V)+2(y+z)(V)=6.8(V)$$

という式が成り立ちます。

❸の場合では・・・

R2とR4で6.8Vを使い切ります。

よって

$$4y(V)+2(y+z)(V)=6.8(V)$$

という式が成り立ちます。

これで3つの方程式ができました。

$$x+3(x-z)=6.8$$

$$x+5z+2(y+z)=6.8$$

$$4y+2(y+z)=6.8$$

これを連立方程式として解くのです。

（上の式をx＝・・・の形に、下の式をy＝・・・の形に変形して、真ん中の式に代入するのがはやいと思います。）

これらを解いて

$$x=2，y=1，z=0.4$$

となります。

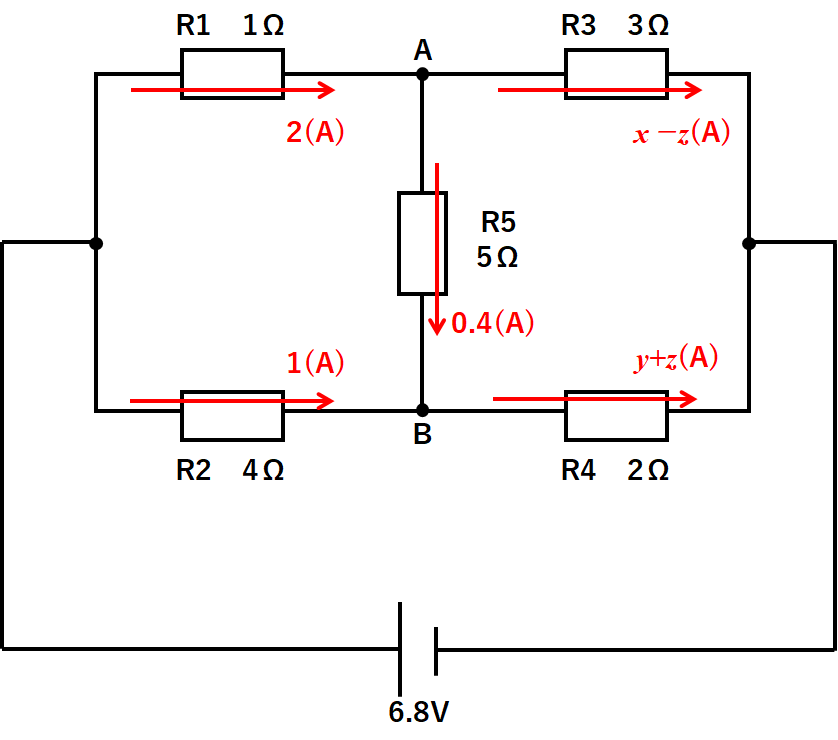
よってR1・R2・R5に流れる電流は↓のようになっています。

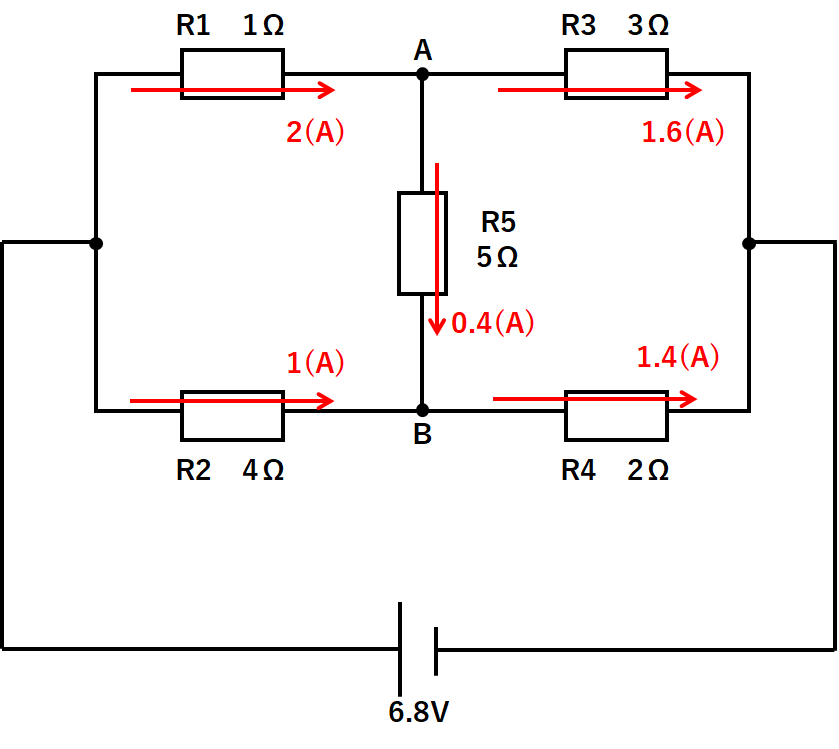
ここからR3・R4の電流を求めると↓のようになります。

よってR5に流れる電流は0.4Aとなります。

この解法はパターン❶にも適用できる万能な解法です。

しかし未知数がx・y・zの3つある連立方程式を解かなければなりません。

それなりの計算能力が要求されるのです。

よってブリッジ回路の問題は以下のように解法を探りましょう。

①　R1×R4＝R2×R3になっていれば中央の電流は0A。

②　①ではないパターン❶ならば次のように書き換え。

③　①ではないパターン❷ならば3か所の電流を文字設定し連立方程式をつくる。