*このページは発展的な内容を含みます。
このページではイタリアの学者トリチェリさんが大気圧をどのようにして計測したかを、中学理科レベルの知識で紹介しています。
※圧力については→【圧力】←を参考に。
※大気圧については→【大気圧】←を参考に。
※密度については→【密度】←を参考に。
以上を習得していないと理解は難しいです。
動画による解説は↓↓↓
チャンネル登録はこちらから↓↓↓
1.大気圧の測定
大気圧の大きさを測定したのはイタリアのトリチェリさんです。
彼は水銀を利用して大気圧に関する実験を行いました。
トリチェリがどのような実験をしたのか見てみましょう。
まず長~い試験管のようなものを準備しました。
だいたい1mくらいのものです。
この試験管のようなものに水銀を目一杯入れます。(↓の図)
水銀は金属ですが、「ふつうの気温では液体である」という変わった金属です。
もう1つ水銀を入れた容器を用意しておきます。
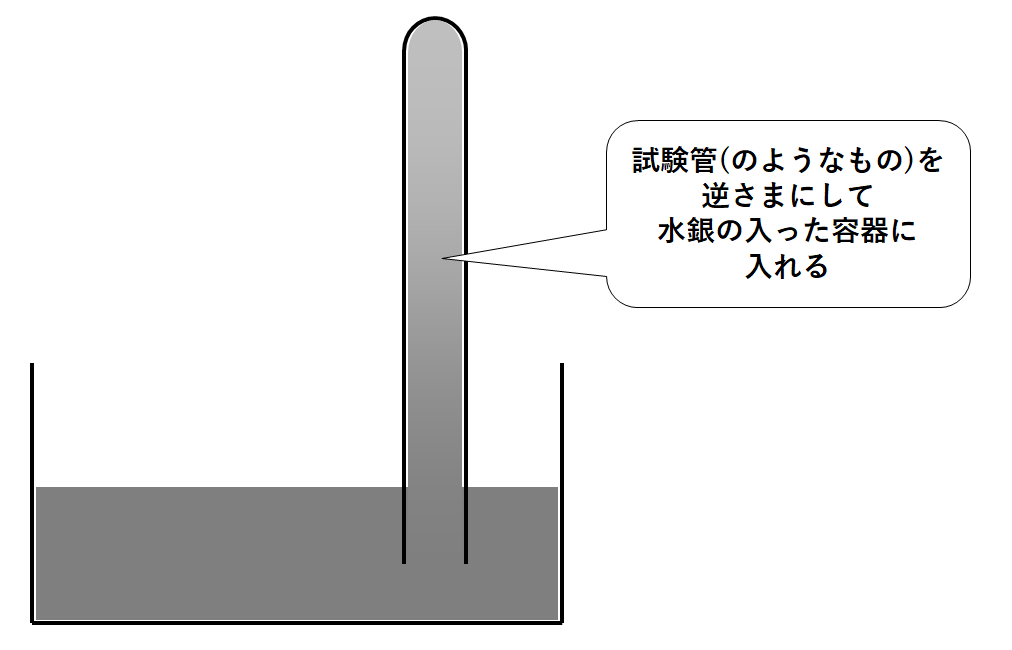
先ほどの水銀が入った試験管を逆さまにして、空気が入らないように注意しながら容器に入れます。(↓の図)
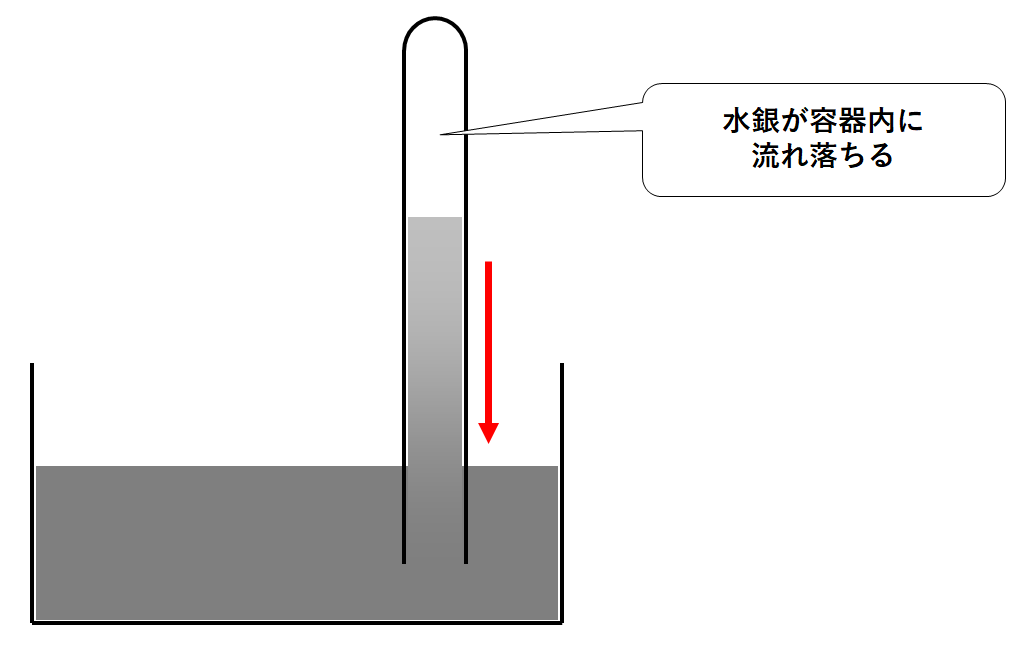
そうすると水銀はどんどん容器の中に流れ落ちていきます。(↓の図)
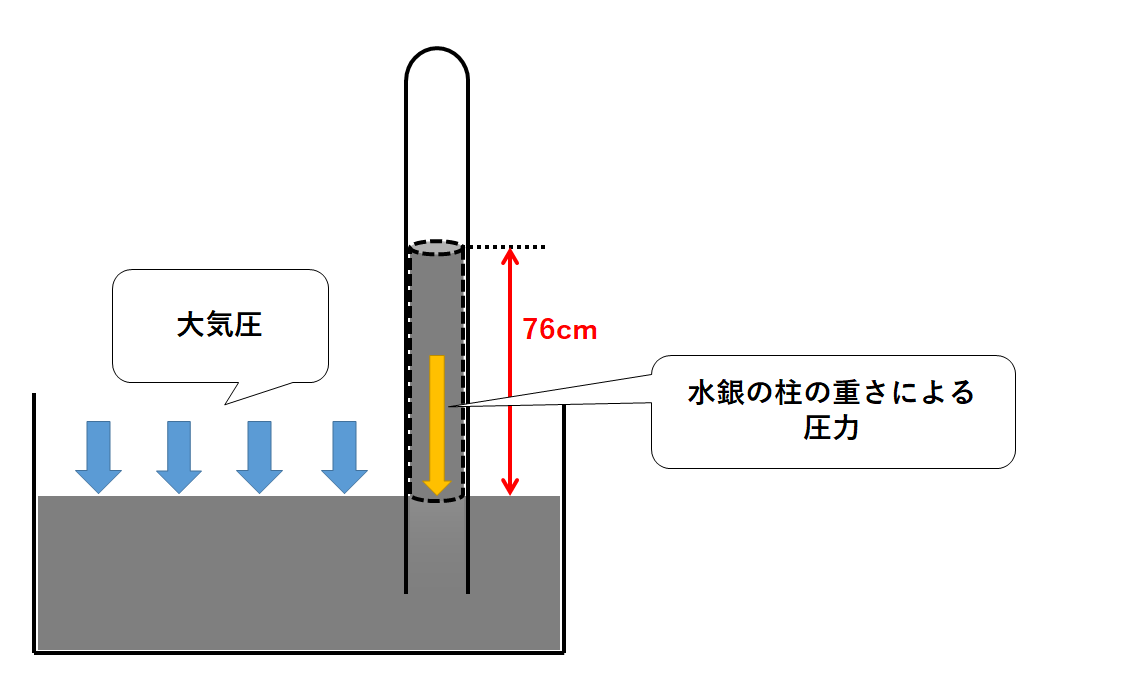
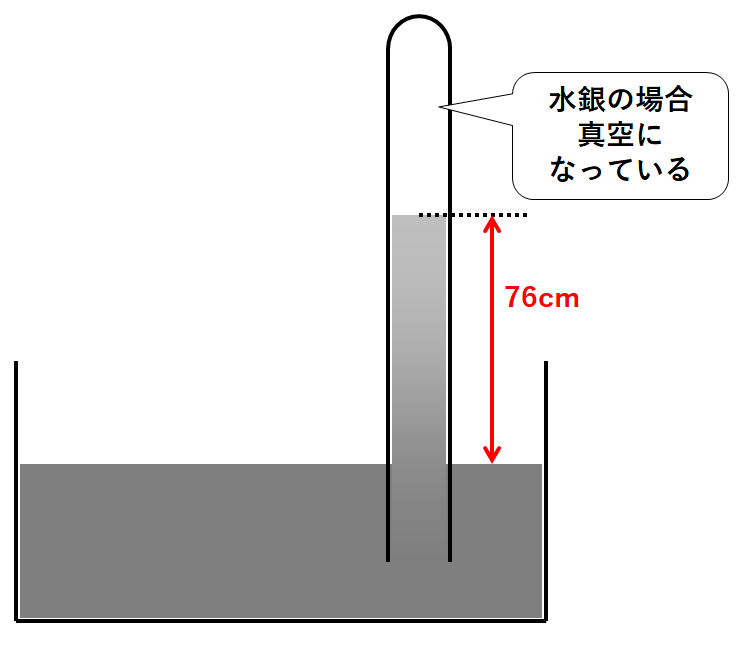
しかし水銀は76cmの高さで止まり、流れ落ちなくなります。(↓の図)
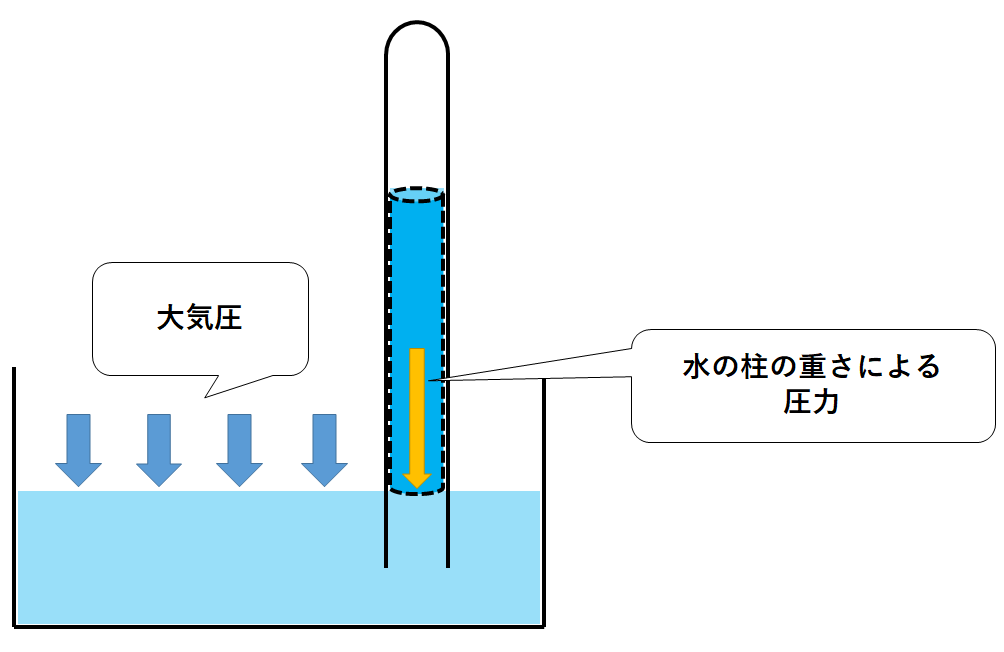
これは試験管内の水銀の柱による圧力と大気圧がつりあっているため起こる現象です。
つまり水銀の柱による圧力を求めてみれば、大気圧が求まるというわけです。
では、水銀の柱による圧力を求めてみましょう。
ここでこの試験管のようなものの断面積は1cm2とします。
また水銀の密度はおよそ13.6g/cm3です。
まず水銀の柱の体積を求めましょう。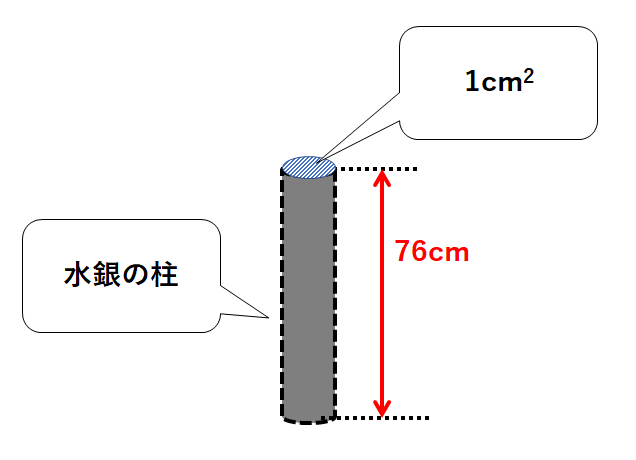
$$体積=底面積×高さ1cm^2×76cm=76cm^3$$
水銀の密度は13.6g/cm3であるので、この水銀の質量は
$$水銀の質量=体積×密度$$
$$=76cm^3×13.6g/cm^3=1033.6g$$
これを重さ(N)に直すと
$$1033.6g⇒10.336N$$
となりますが・・・
ふだん中学理科では100gの物体にはたらく重力を1Nとします。
しかしこれは正確な値ではありません。
正しくは100gの物体にはたらく重力は0.98Nなのです。
よって1033.6gの水銀の柱にはたらく重力をx(N)とすると
$$100g:0.98N=1033.6g:x(N)$$
$$x=10.12928(N)$$
となります。
よってこの水銀の柱による圧力は
$$圧力=力÷面積$$
$$=10.12928(N)÷\frac{1}{10000}m^2=101292.8N/m^2$$
単位を変えましょう。
$$1hPa=100Pa=100N/m^2$$
であるので
$$101292.8N/m^2=101292.8Pa=1012.928hPa$$
およそ1013hPaという数字が出てきました。
このようにしてトリチェリは大気圧が1013hPaであることを調べました。
以上のようにトリチェリは水銀を使いました。
しかし水銀は有毒であり、扱いが難しい物質です。
ほかの物質ではできなかったのでしょうか?
例えば水、とか。
2.水を用いて大気圧を測定してみる
というわけで水の場合はどのようになるか計算してみます。
ここでこの試験管のようなものの断面積を1cm2とします。
100gの物体にはたらく重力は1Nで計算します。
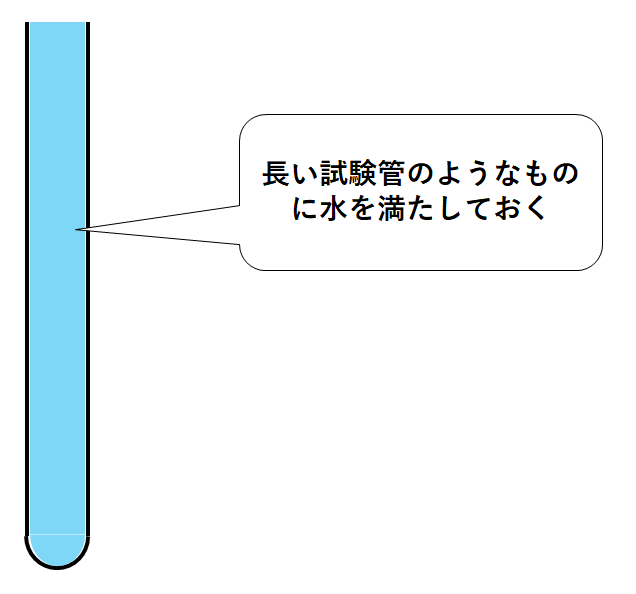
まず長ーい試験管のようなものを準備します。
そこに水を満たしておきます。(↓の図)
そしてもう1つ水を入れた容器を用意。
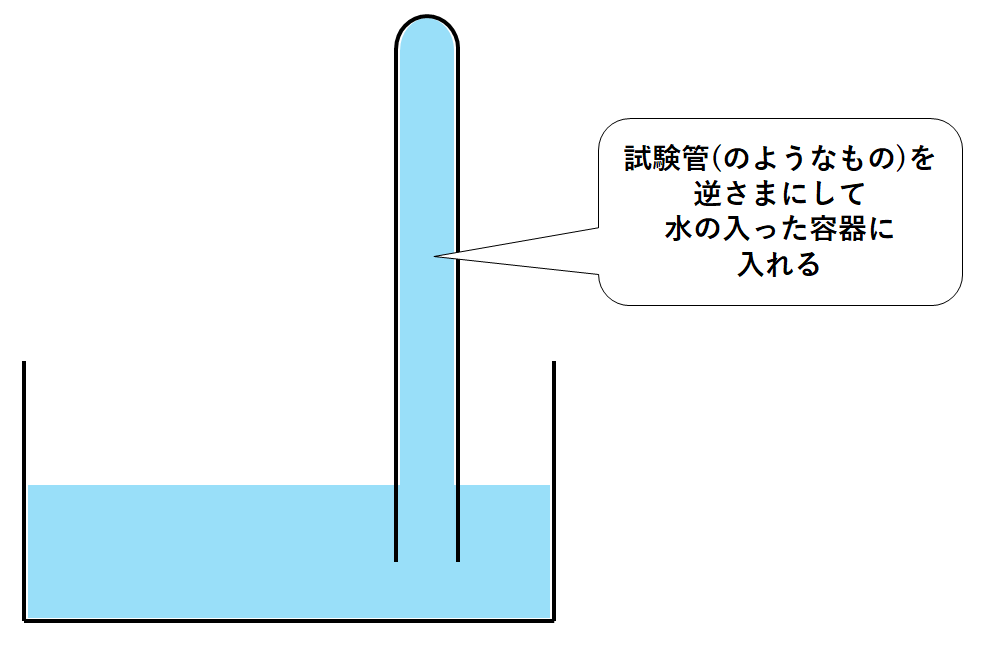
先ほどの試験管(のようなもの)を逆さまにして、空気が入らないように注意しながら容器に入れます。(↓の図)
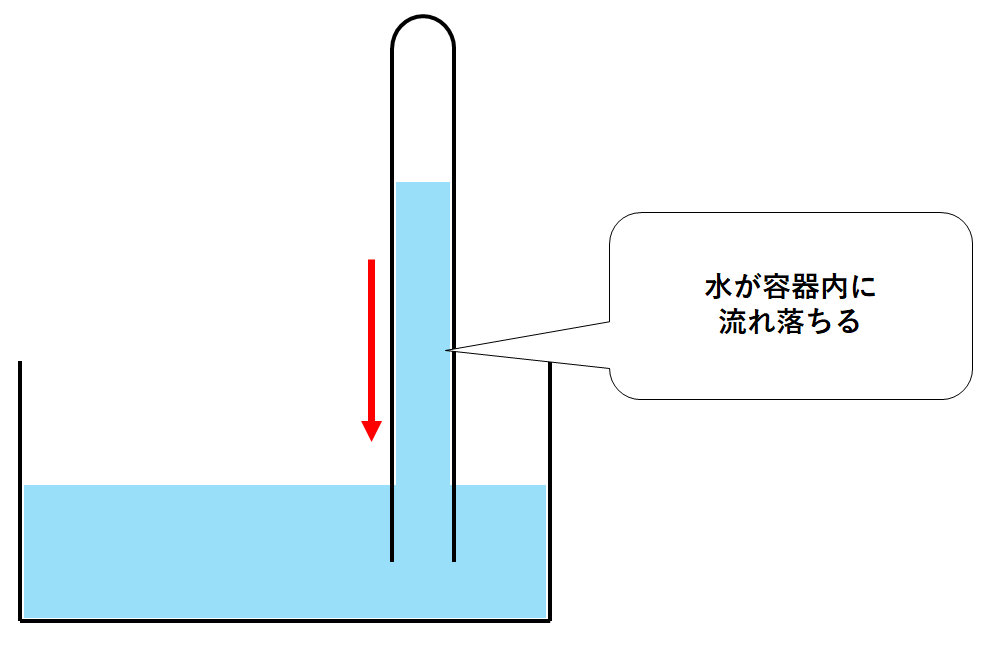
先ほどと同様、試験管内の水はどんどん容器の中に流れ落ちていきます。(↓の図)
がある高さで止まり、流れ落ちなくなるはずです。(↓の図)
このときの水の柱が何cmになるか調べてみます。
水の柱がx(cm)であるとすると
水の柱の体積は
$$底面積×高さ=1(cm^2)×x(cm)=x(cm^3)$$
水の密度は1g/cm3なので、この水の質量は
$$質量=体積×密度=x(cm^3)×1g/cm^3=x(g)$$
100gの物体にはたらく重力は1Nであるとして、これを重さ(N)に直すと
$$x(g)⇒\frac{x}{100}(N)$$
よって水の重さによる圧力は
$$圧力=力÷面積$$
$$=\frac{x}{100}(N)÷\frac{1}{10000}(m^2)=100x(N/m^2)$$
となります。
単位をhPaに直しましょう。
$$100x(N/m^2)=100x(Pa)=x(hPa)$$
これが大気圧1013hPaと等しいので
$$x(hPa)=1013hPa$$
つまりx=1013となります。
xは水の柱の高さ(cm)ですから、1013cmの高さの水の柱ができるのです。
おおよそ10mです。
そのような試験管のような管を準備するのは難しいですよね。
それだけではありません。
水銀の沸点は約356度。ふつうの気温では、カンタンに気体になることはありません。
なので、↓のように真空の部分ができます。
しかし水の場合。
水はすぐ蒸発してしまいます(気体になってしまう)。
つまり↓のように、水銀では真空だった部分に水蒸気が入り込みます。
これでは水蒸気による気圧も考慮せざるを得ません。
そのため、正確な測定が難しくなります。
よって水銀で行うのがもっとも現実的な方法なのです。
POINT!!
・圧力=力÷面積で求められます。
・トリチェリーの実験では
「水銀の重さによる圧力=大気圧」となっています。
・これにより大気圧は1013hPaと測定されました。




コメント(承認された場合のみ表示されます)
トリチェリ の実験で試験管を斜めに入れた場合でも高さが76cmになる理由が分からないです。
本文中;「水銀の柱の体積は斜めを向いていようといまいと「底面積×高さ」で求められます。よって底面積と高さが同じであれば、体積は等しいのです。」
「体積」とは?、何の体積であろうか? 図を見る限り(あるいは、もっと試験管をネカセタ状態を想像すれば、より明確に)より垂直に近い場合と、斜めに配置された場合の体積は違うように思われますが?
最後の説明(図中)の、「体積は同じ」は明らかな間違いと思いますから、(間違いなら間違いと)きちんと訂正すべきです。
taniguchi hiroshi様、コメントありがとうございます。
自分が重大な勘違いをしておりました。
誠に申し訳ありません。
確かに左右で体積は同じでありません。
基本的な勘違いを犯しており、情けない限りです。
訂正した解説を以下に記載しておきます。
のちのち本文にも追記しようと思います。
=============
左は管を水銀の液面に垂直に立てたようす。
このとき水銀柱の高さが76cmになるのは上記の説明の通り。
この水銀柱の底面積(オレンジ)を1(cm2)とする。
次に斜めに向けた場合が右図。
このときの水銀柱の底面積は、左よりも少し大きい。
右の底面積が左のk倍であるとする。
つまり右の底面積はk(cm2)=0.0001k(m2)
左の水銀柱の体積は76cm3。
右の水銀柱の体積は76k(cm3)。
体積もk倍になっている。
ということは質量や重さもk倍になっている。
本文中の数字を使うと左の水銀柱の重さ=10.12928N
右の水銀柱の重さはそのk倍なので10.12928k(N)。
オレンジの面に及ぼす圧力を求めると
左の場合=10.12928N÷0.0001m2=101292.8N/m2
右の場合=10.12928k(N)÷0.0001km2=101292.8N/m2
このようにどちらの水銀柱でもオレンジの面に及ぼす圧力は同じ。
つまり斜めを向けたとしても
・底面積がk倍
・水銀柱76cm分の重さもk倍
・そのため水銀柱の重さによる圧力は変わらない
よって水銀柱の液面からの高さは76cmになる。
この説明に頼ると、上に行くほど先が細くなるような管だと、
水銀柱の高さが76cmより高くなってしまいますね。
つまり、この説明では本質の理解という点で無理があります。
中学理科の段階で、あまり説明に踏み込まない方がいいのではないですか?
もしくはそんな気づきができる中高生と
対話的な学びを進めていただければと思います。
ぶつりんご様
コメントありがとうございます。
トリチェリがおっしゃるような「上に行くほど細くなる管」を本当に使っていたのであれば、説明を変えねばならないかもしれませんね。
貴重なご意見ありがとうございます。