中3地学【*星の明るさ・等級】

*このページは発展的な内容を含みます。

1．星の明るさ

■等級

星の明るさを示す単位のこと。

もともと空に見える星を、明るさのちがいで

1等星・2等星・3等星・4等星・5等星・6等星

（左のものほど明るく、右のものほど暗い）

と6つに分類していました。

もっとも明るい星を「1等星」と呼び、目に見えるぎりぎりの明るさの星を「6等星」としていました。

現在ではより細かく分類するために、それぞれの星が等級で分類されています。

この等級が小さいほど明るく、大きいほど暗いです。

具体的には等級が1.0小さくなると明るさは2.5倍増します。

例えば・・・

「3.0等級の恒星A」と「2.0等級の恒星B」があります。

恒星Aの方が恒星Bよりも等級が大きいですね。

つまり恒星Bの方が明るいということです。

その差は

3.0等級－2.0等級＝1.0等級

ですから

恒星Bの方が2.5倍明るいと言えます。

さらに・・・

「3.0等級の恒星A」と「2.0等級の恒星B」以外に「1.0等級の恒星C」があったとしましょう。

恒星Cの等級がもっとも小さいのでCが最も明るい恒星と言えます。

では恒星Bと恒星Cを比べてみましょう。

その等級の差は

2.0等級－1.0等級＝1.0等級

です。

よって
恒星Cの方がBよりも2.5倍明るいと言えます。

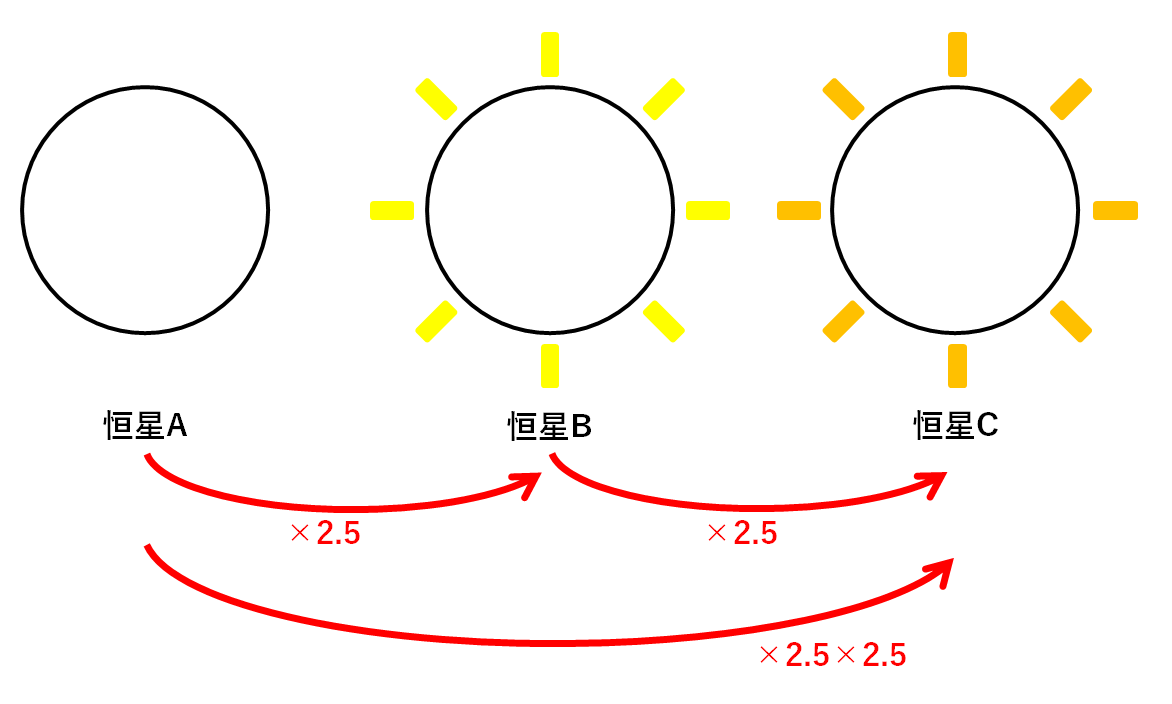
ここで恒星Aと恒星Cを比べてみます。

・恒星Bは恒星Aよりも2.5倍明るい

・恒星Cは恒星Bよりも2.5倍明るい

ということは

恒星Cは恒星Aよりも

2.5×2.5＝2.5²＝6.25倍

明るい星となります。(↓の図)

今の話をまとめましょう。

等級が1.0小さくなると、明るさは2.5倍増します。

では

等級が2.0小さくなると・・・

明るさは2.5²倍＝6.25倍増すということです。

(2.5×2＝5.0倍明るくなる、は間違いですので注意！)

さらにさらに・・・

「3.0等級の恒星A」・「2.0等級の恒星B」・「1.0等級の恒星C」以外に「－1.0等級の恒星D」があったとしましょう。

Dは等級が負の数なので、4つの恒星でもっとも明るいことになります。
（このように負の数になることもあります。太陽は何と－26.7等級です！）

恒星Aと恒星Dの明るさを比べると

その等級の差は

3.0等級－(－1.0等級)＝4.0等級

となります。

つまり明るさはDの方が

2.5⁴＝39.0625倍

明るいことになります。

2．見かけの等級と絶対等級

ある明るさの恒星Xがあるとします。

恒星Xの間近で観測した場合の明るさと遠いところで観測した場合の明るさは異なります。

間近であればあるほど恒星Xは明るく見えます。

遠く離れていればいるほど恒星Xは暗く見えます。

具体的には、星の明るさは距離の2乗に反比例します。

距離の2乗に反比例とは・・・
$$距離が2倍・3倍・4倍・・・になると、明るさは\frac{1}{2^2}倍・\frac{1}{3^2}倍・\frac{1}{4^2}倍・・・$$
となり
$$距離が\frac{1}{2}倍・\frac{1}{3}倍・\frac{1}{4}倍・・・になると、明るさは2^2倍・3^2倍・4^2倍・・・$$
となることです。

例えば

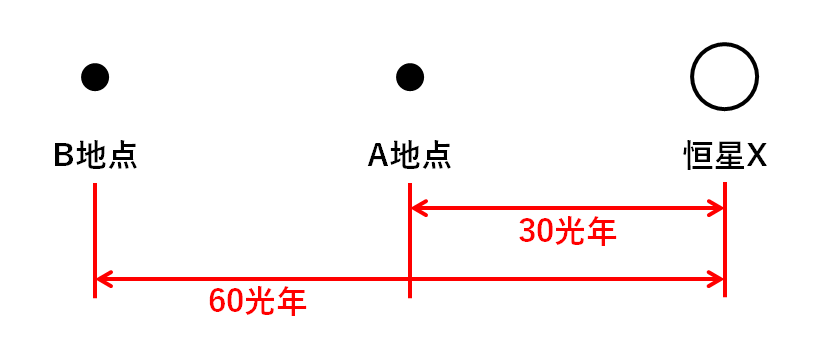
①恒星Xを30光年離れたA地点で観測した場合

②恒星Xを60光年離れたB地点で観測した場合

の明るさを比べてみましょう。

A地点の方が恒星Xに近いので、①の場合の方が明るく見えることがわかります。

その明るさは「距離の2乗に反比例」するので

$$①→②で・・・距離が2倍$$

$$①→②で・・・明るさは\frac{1}{2^2}倍$$

となります。

例題

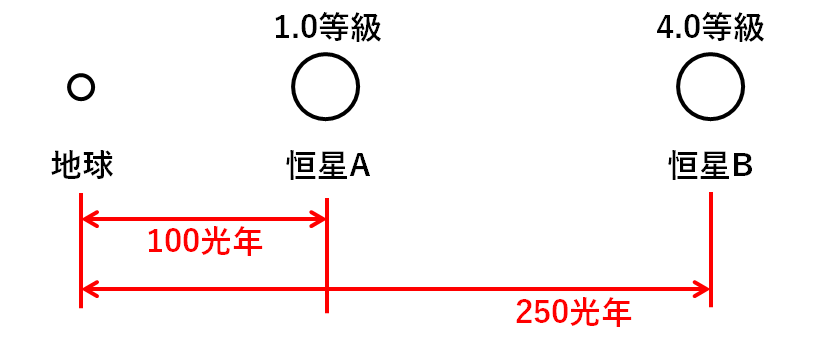
地球から見た明るさが1.0等級の恒星Aと4.0等級の恒星Bがある。

地球から恒星Aまでの距離は100光年、地球から恒星Bまでの距離は250光年である。

（1）地球から見たとき、恒星Aの明るさは恒星Bの明るさの何倍か。四捨五入して整数で答えよ。

（2）恒星Bが地球から100光年のところにあるとすると、地球から見たときの等級はいくらになるか。

(答)

(1)
恒星Aと恒星Bの地球から見たときの等級の差は

4.0等級－1.0等級＝3.0等級

ですので

恒星Aの方がBよりも

$$2.5^3=15.625≒16倍$$

明るいことになります。

(2)

恒星Bは地球から250光年のところにあります。

これを地球から100光年のところに近づけます。

つまり距離が

$$100光年÷250光年=\frac{2}{5}倍$$

になりました。

明るさは距離の2乗に反比例するので

$$\frac{5^2}{2^2}=\frac{25}{4}倍$$

になります。

そして

$$\frac{25}{4}倍=6.25倍=2.5^2倍$$

となります。

等級が1小さくなれば明るさは2.5倍になりました。

いま明るさが2.5²倍になった→等級は2小さくなることになるので、

地球から100光年のところにおいた恒星Bは・・・

4.0等級から2小さくなって2.0等級となります。

このように等級とは、同じ星であってもどこから見るかで変化します。

地球から観測したときのそのままの等級を見かけの等級といいます。

この例題では

地球から100光年のところに置いた恒星Aは1.0等級

地球から250光年のところに置いた恒星Bは4.0等級

地球から100光年のところに置いた恒星Bは2.0等級((2)より)

でした。

つまり地球から等距離に恒星A・Bを置いたとき、Aの方が明るいことがわかります。

このように地球から一定の距離に置いたときの等級を絶対等級といいます。