2018年　大阪府立入試問題　解説

このページでは2018年度の大阪府立入試一般選抜の問題を解説しています。(理科のみ)

問題・模範解答はこちら↓↓
http://www.pref.osaka.lg.jp/kotogakko/gakuji-g3/h30_gakken.html

大問1の解説

(1)(2)

・水に溶けにくい気体→水上置換法
(例)酸素・水素・*二酸化炭素・窒素

・水に溶けやすく空気より軽い気体→上方置換法
(例)アンモニア

・水に溶けやすく空気より重い気体→下方置換法
(例)*二酸化炭素・塩素

*二酸化炭素は水に少し溶けて、空気より重い気体です。
水上置換法と下方置換法の両方で集めることができます。

(6)

亜鉛原子の陽子の数は、問題文より30個。

原子では(陽子の数)＝(電子の数)となっているので
亜鉛原子の電子の数は30個。

亜鉛原子は、電子を2個失って亜鉛イオン(Zn^2＋)となるので
亜鉛イオンの電子の数は28個となります。

★次のことを押さえておきましょう。
陽イオン・・・原子が電子を失ってできる。
陰イオン・・・原子が電子を得てできる。

(7)(8)

電池に必要なのは
①電解質の水溶液
②イオン化傾向の異なる2枚の金属板
です。

①については砂糖水・エタノール・蒸留水(純水のこと)が適さないということを覚えておきましょう。

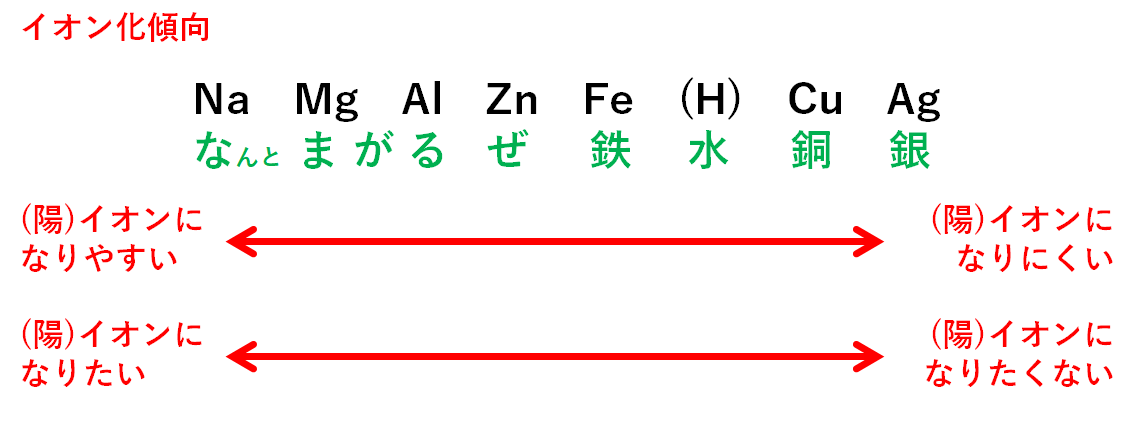
②については次の順番を覚えましょう。

これはそれぞれの元素をイオンになりやすいものから順に並べたものです。
(この「イオンにどれくらいなりやすいか」をイオン化傾向といいます)

・イオン化傾向の大きな金属では・・・
金属板そのものが電子を失い、陽イオンへと変化します。
よって電池の－極となり、電解質水溶液中に溶けだしてしまいます。

・イオン化傾向の小さな金属では・・・
一方の金属板が失った電子がやってきます。
金属板に近づいてきた水素イオンがこの電子を得て、水素原子が生じます。
よって電池の＋極となり、水素が発生します。

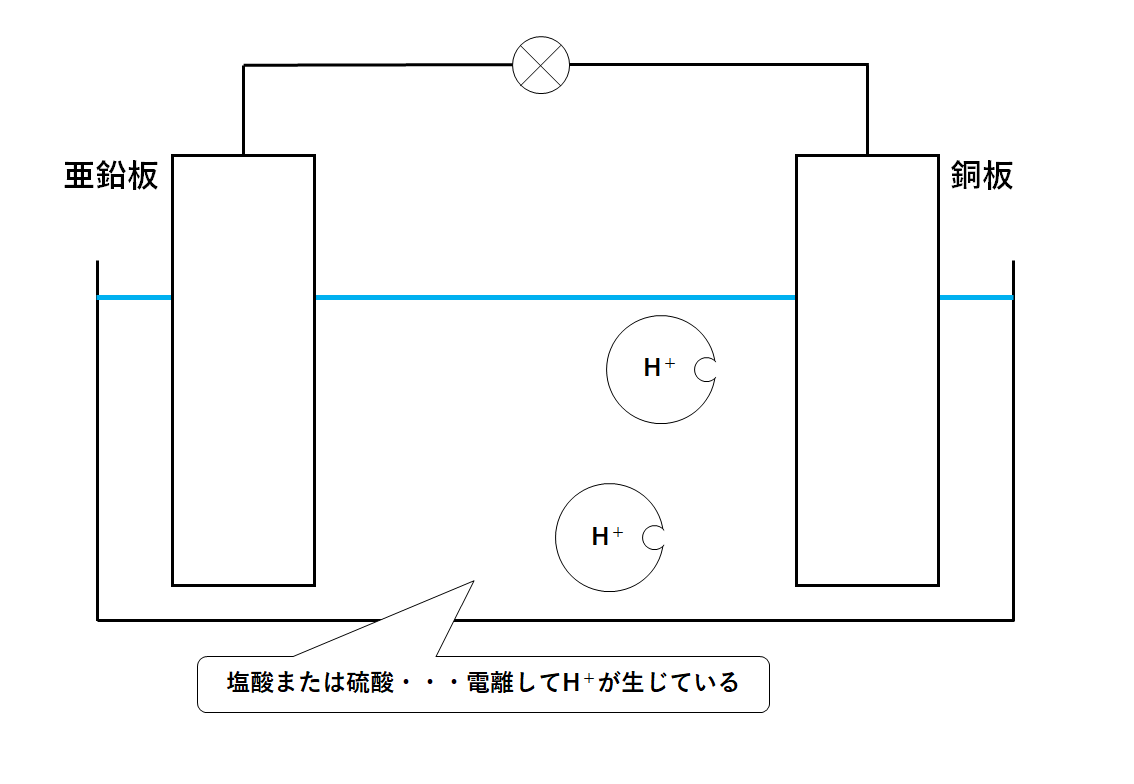
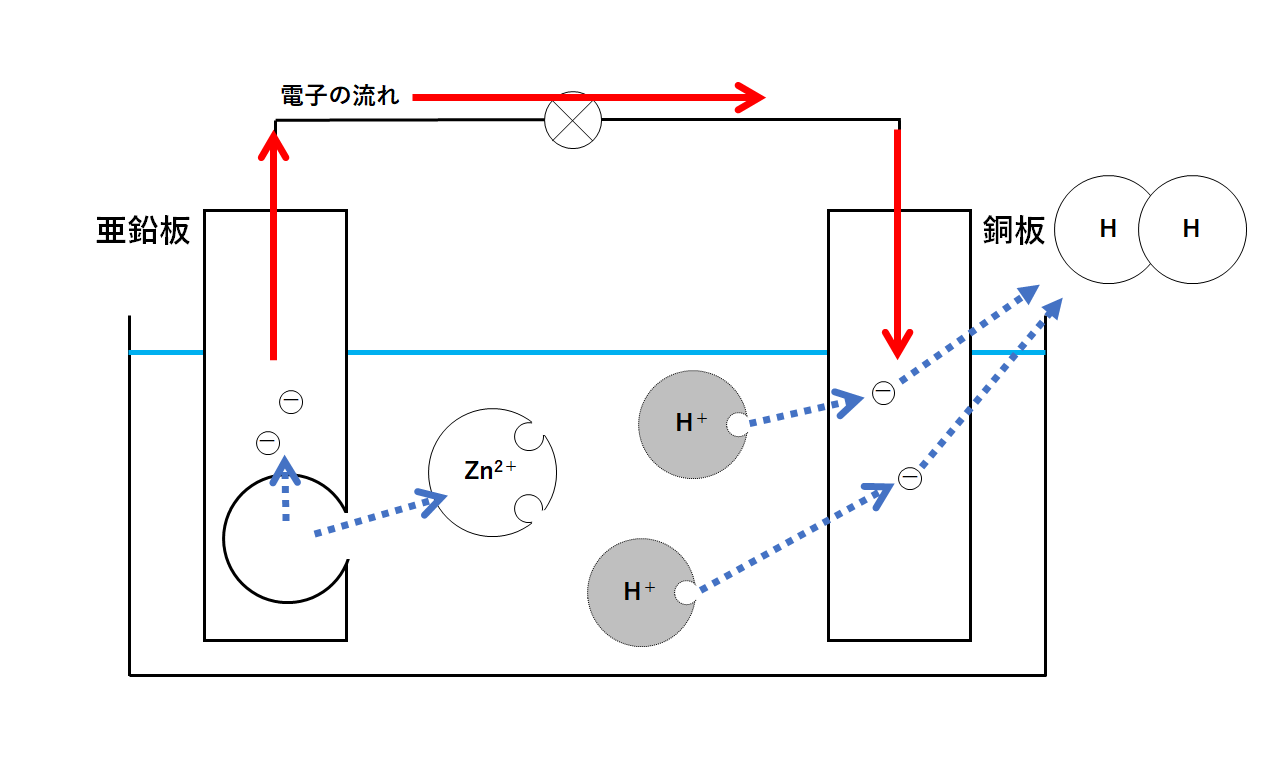
↓の図は亜鉛板と銅板・塩酸(または硫酸)によってつくられた電池です。

この電池では次のようなことが起こっています。

・イオン化傾向の大きい亜鉛板
亜鉛板の一部が電子を失い、亜鉛イオンとして溶けだす。

・イオン化傾向の小さい銅板
水溶液中の水素イオンが電子(亜鉛板からやってきたもの)を得て、水素原子ができる。
水素原子が2個集まり、水素分子(水素の気体)が発生する。

詳しくは→【電池のしくみ】←を参考に。

(9)

電子から取り出せる電圧は、イオン化傾向の差によって決まります。
イオン化傾向の差が大きい金属であるほど、電圧の大きな電池となります。

また前問で書いた通り、
イオン化傾向の大きい方→－極
イオン化傾向の小さい方→＋極
となります。

表Ⅰより

銅とニッケルでは
(イオン化傾向　大)←　ニッケル・銅　→(イオン化傾向　小)

亜鉛とマグネシウムでは
(イオン化傾向　大)←　マグネシウム・亜鉛　→(イオン化傾向　小)

ニッケルとマグネシウムでは
(イオン化傾向　大)←　マグネシウム・ニッケル　→(イオン化傾向　小)

以上のような順になります。

これをまとめるとこの4つの金属の中で
もっともイオン化傾向の大きな金属はマグネシウム
もっともイオン化傾向の小さな金属は銅
とわかります。

大問2の解説

(1)

風(空気の流れ)は気圧の差によって生じます。
風は気圧の高い方から低い方へ吹きます。

あたたかい空気は密度が小さいため、上昇します。
すると地表の気圧は低くなります。

つめたい空気は密度が大きく、下降します。
すると地表の気圧は高くなります。

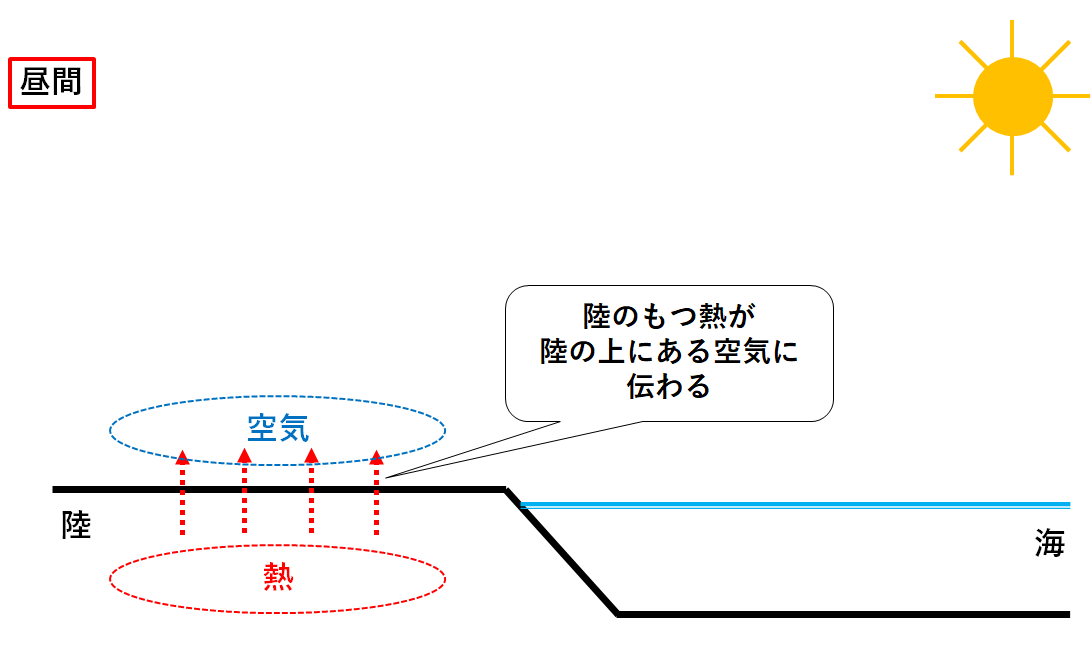
陸と海を比べたとき
陸はあたたまりやすく、冷めやすい性質があります。
海はあたたまりにくいですが、冷めにくい性質があります。
そのため、昼の間は陸の方があたたかくなります。

つまり陸の気圧が下がります。

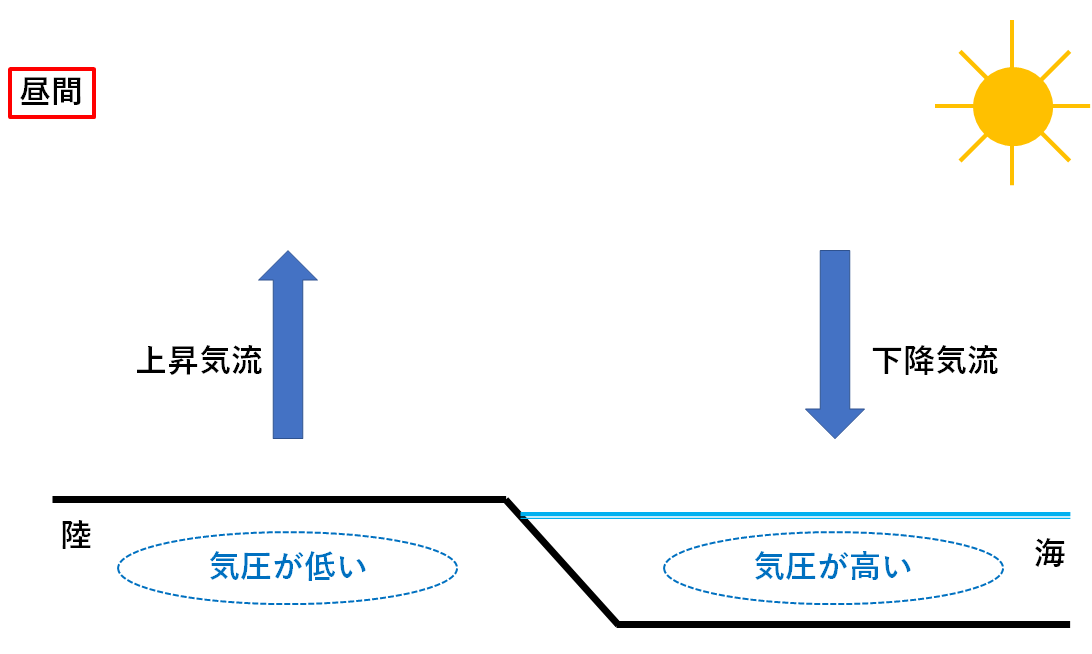
そのため海から陸へ風が吹きます。(気圧の高い方から低い方へ)

この風を海風といいます。

一方で、夜の間は海の方があたたかくなります。
つまり海の気圧が下がります。
そのため陸から海へ風が吹きます。(気圧の高い方から低い方へ)
この風を陸風といいます。

(2)

風の強さは等圧線の間隔から判断できます。
等圧線の間隔がせまい→風が強い
等圧線の間隔が広い　→風が弱い

(3)

表Ⅰより
大阪の最高気温は33.5℃・最低気温は25.8℃
デリーの最高気温は43.2℃・最低気温は25.8℃
です。
気温差が大きいのはデリーですね。

また表Ⅰより
大阪の湿度はおおむね60%～70%、
デリーでは、特に12時以降20%前後
ですので大阪の方が湿度が高いことがわかります。

(6)

金属製のコップの表面がくもり始める温度とは
空気中の水蒸気が冷えて、水滴がつく温度のこと。
つまりは露点です。
※「くもる」という表現は細かな水滴がつくことを意味します。

露点を求めるためには実際の水蒸気量を求めておくことが必要です。
※露点とははじめて飽和水蒸気量＜実際の水蒸気量となる温度でもあります。

湿度の公式は
$$湿度=\frac{実際の水蒸気量}{飽和水蒸気量}×100$$

この式から実際の水蒸気量を求めるには
$$実際の水蒸気量=飽和水蒸気量×\frac{湿度}{100}$$
を計算すればいいことになります。
※非常によく使う式ですので覚えておくと便利です。

この部屋の気温は34℃(乾球温度計の目盛りより)。
よって飽和水蒸気量は37.6g/m³。
また(4)より湿度は68％。

よって
$$実際の水蒸気量=37.6×\frac{68}{100}=25.568g/m^3$$

表Ⅳからおよそ27℃を下回れば、
飽和水蒸気量＜実際の水蒸気量となり、水滴が生じることがわかります。

つまり露点は27℃です。

(7)(8)

素焼きの壺が冷える原理を見てみましょう。

根本にあるのは
液体が蒸発する(気体になる)ときまわりの熱を吸収するという原理です。

例えば汗。

わたしたちは暑いときに汗をかきます。
この汗は放っておくと蒸発し気体になります。

液体が気体になるためには熱が必要でなんですね。
よって汗が気体になるときに皮膚の熱を吸収します。
それにより皮膚の温度が下がるのです。

湿球温度計も同様です。

湿球温度計は乾球温度計よりも低い値を示します。
それは湿球温度計の球部のまわりの水分が蒸発した際、球部の熱を吸収するためです。

この素焼きの壺の場合。
問題文より、素焼きの壺には水が入っていて、素焼きの壺の表面には小さな穴が開いています。
この小さな穴から少し水がしみ出します。

しみ出た水分は蒸発するときに、壺や壺の中の水の熱を吸収します。
それにより壺や壺の中の水が冷やされる、というわけです。

よって壺からしみ出た水がたくさんであればあるほど、よく冷えるはず。

そのためには、まわりの空気があまり水蒸気をもっていないほうが良いですね。
すなわち周囲の空気中の実際の水蒸気量が小さい、ということです。

そのためには先ほどの式
$$実際の水蒸気量=飽和水蒸気量×\frac{湿度}{100}$$
より

・気温が高い(＝飽和水蒸気量が大)
・湿度が低い
という状況ならば
周囲の空気中の実際の水蒸気量が小さいことになります。

よって(7)はイの選択肢が正解となります。

大問3の解説

(1)

赤く染まった部分＝根から吸収した水が通った＝道管を表します。

(2)

道管・・・・根から吸収した水を運ぶ管
師管・・・・葉でできた栄養分を運ぶ管
道管と師管をまとめて維管束と呼びます。

(4)

記録1より・・・
ホウセンカの花にはSを持つもの・Tを持つものの2種類があるとわかります。

記録2より・・・
開花直後のホウセンカにはTが見られる。
そしてTには花粉が見られるので、Tにはおしべが含まれていることがわかります。

記録3より・・・
Tの内部には緑色の粒が含まれるとわかります。

記録4より・・・
Tは、そのまわりがとれてSのようになることがわかります。

記録5より・・・
種子が見られたことから
Sにはめしべが含まれることがあるとわかります。
また記録3の緑色の粒が胚珠であるとわかります。

これらをまとめると
Sはめしべ
Tはめしべのまわりをおしべがおおったもの
とわかります。

開花直後ではTのようになっていますが
数日後にSのようにおしべがなくなります。

よって③はウが正解となります。

大問4の解説

(2)

問われているのは
Mの電気抵抗の大きさを変化させたとき、Mに加わる電圧がどう変化するか
です。

ならばMの抵抗を0Ω・50Ω・100Ωと仮定して計算してみましょう。

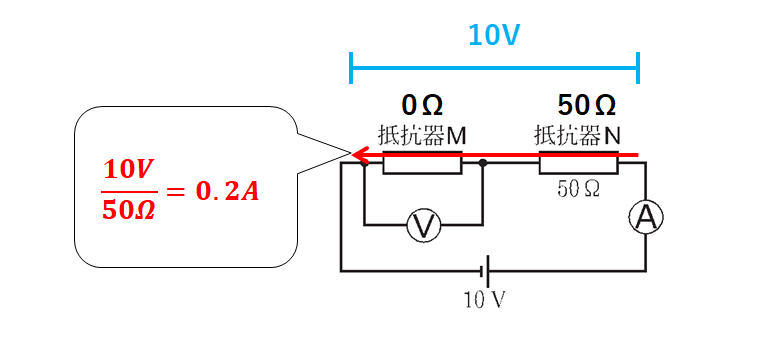
・Mの抵抗が0Ωのとき

回路全体には
$$\frac{10V}{50V}=0.2A$$
の電流が流れます。

Mの抵抗は0Ωなので
$$Mの電圧=0Ω×0.2A=0V$$
となります。

この時点でイ・エの選択肢は適さないとわかります。

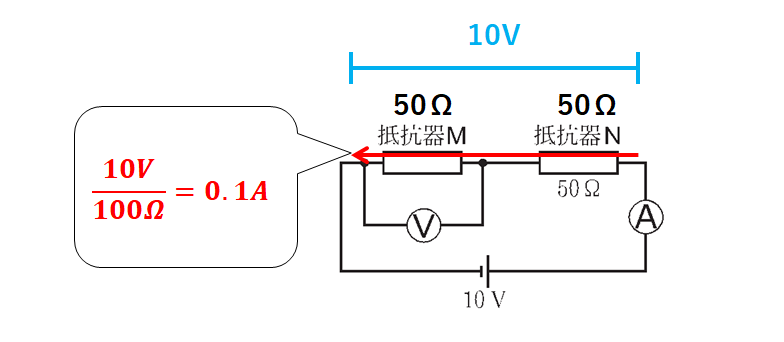
・Mの抵抗が50Ωのとき

回路全体には
$$\frac{10V}{100Ω} =0.1A$$
の電流が流れます。

Mの抵抗は50Ωなので
$$Mの電圧=50Ω×0.1A=5V$$
となります。

この時点でアは適さず、ウが正解とわかります。

(3)

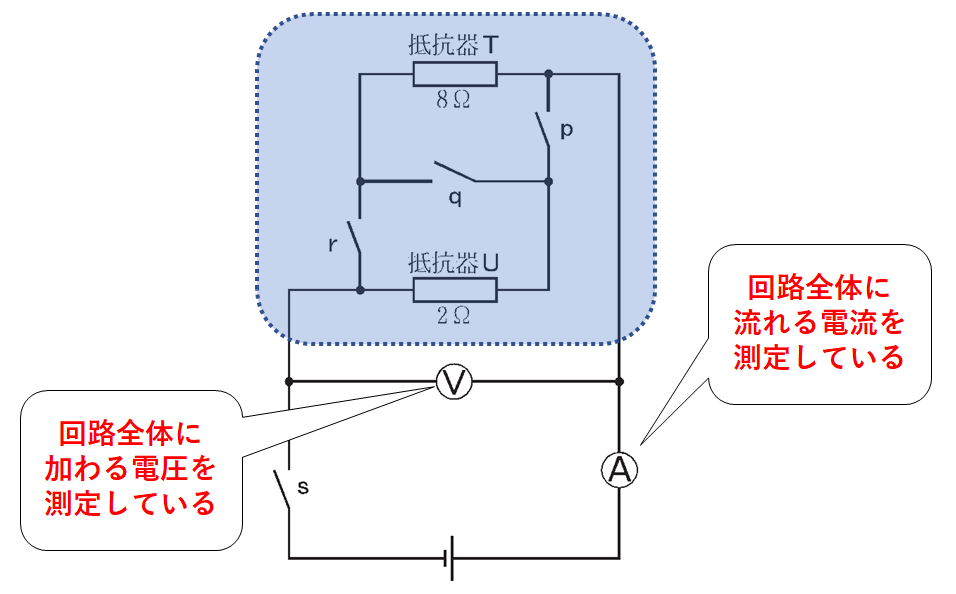
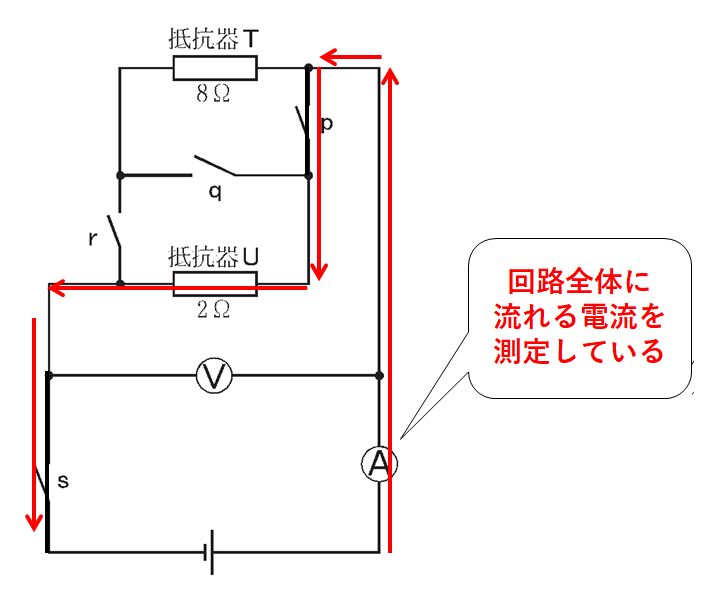
この回路では
電流計は回路全体の電流を測定し
電圧計は回路全体の電圧を測定する
ように接続されています。

電圧計の値と電流計の値で回路全体の抵抗が求められるわけです。

この問いでは
電流計・・・1.5A
電圧計・・・3V
なので

回路全体の抵抗は
$$\frac{3V}{1.5A}=2Ω$$
となります。

つまり電流が流れた抵抗器は抵抗器Uのみ。
抵抗器Uのみに電流が流れるようにするためにはp・sのスイッチを入にしなければいけません。

よってアが正解となります。

(4)

「電流計の示す値が0ではない最も小さい値になる」
とあるので
もっとも電流が流れにくい回路である必要があります。

電流が流れにくい＝回路全体の抵抗が大きい
ということなので
抵抗器UとTを直列につながなければいけません。

※次を押さえておこう。
抵抗を直列につなぐ→合成抵抗が大→電流は流れにくい
抵抗を並列につなぐ→合成抵抗が小→電流は流れやすい

よってqとsのスイッチを入にすればよいことになります。

(5)①

熱量の求め方は
$$熱量(J)=電力(W)×時間(秒)$$
です。

また電力は
$$電力(W)=電流(A)×電圧(V)$$
で求まります。

よってこの場合の回路全体の電力は
$$電力(W)=1.5A×6V=9W$$

発生する熱量は
$$熱量(J)=9W×180秒=1620J$$
となります。

(5)②

この問いでは電熱線XとZ1本ずつを並列回路になるようにつないでいます。(↓の図)

Xの抵抗は12Ω、回路全体の電流が1.5A、回路全体の電圧が6Vです。

ここからXに流れる電流は
$$\frac{6V}{12Ω}=0.5A$$

よってZに流れている電流は
$$1.5A-0.5A=1A$$

したがってZの抵抗は
$$\frac{6V}{1A}=6Ω$$
となります。

(6)

もっとも短い時間で水温を3℃上昇させるには
電力が大きい必要があります。

※水の上昇温度は熱量で決まります。
熱量(J)＝電力(W)×時間(秒)
なので
短時間にたくさんの熱量を出すためには電力が大きい必要がありますね。

電圧はどの場合でも6Vで一定のとき、電流が大きいと電力も大きくなります。

電流を大きくするためには、回路全体の抵抗が小さくなければいけません。
よって電熱線を並列につなげばよいのです。
((4)でも同じ説明をしました)

イ・エ・カのどれかが正解の選択肢です。

並列回路の合成抵抗は
$$合成抵抗=\frac{抵抗の積}{抵抗の和}$$
で求まるので

イの場合の合成抵抗は
$$合成抵抗=\frac{12×5}{12+5}=\frac{60}{17}Ω$$

エの場合の合成抵抗は
$$合成抵抗=\frac{12×12}{12+12}=6Ω$$

カの場合の合成抵抗は
$$合成抵抗=\frac{5×5}{5+5}=2.5Ω$$

回路全体の抵抗が小さいのはカの選択肢となります。

(7)

求める時間をx(秒)としましょう。

電熱線から発生する熱量は
$$1000W×x(秒)=1000x(J)$$

このうち90%が水温の上昇に使われるので、その熱量は
$$1000x(J)×\frac{90}{100}=900x(J)$$
です。

これが450000Jと等しいはずなので
$$900x=450000$$

よってx＝500秒となります。

大阪府公立高等学校 一般入学者選抜 CD付 2019年度受験用 赤本 30271 (公立高校入試対策シリーズ)

posted with ヨメレバ

英俊社 2018-06-16

Amazon

楽天ブックス