2019年　大阪府公立入試問題　解説

このページでは2019年度(令和元年・平成31年)の3月に実施された大阪府立入試の理科の問題の解説を掲載しています。

問題などは↓↓↓に掲載されています。
http://www.pref.osaka.lg.jp/kotogakko/gakuji-g3/h31gakken_ippan.html

大問1の解説

(1)

メダカは魚類です。

哺乳類は恒温動物ですが、魚類は変温動物のため、アは誤り。

哺乳類、魚類ともに有性生殖でなかまをふやすので、イも誤り。

哺乳類、魚類ともにせきつい動物であるので、ウは正しい選択肢。

外とう膜で内臓がおおわれているのは軟体動物の特徴。エも誤り。

(2)

動脈と静脈をつなぐ非常に細い血管を毛細血管といいます。

また血液には固形成分と液体成分があります。

固形成分は以下の3つ。

・赤血球・・・酸素を運ぶ。

・白血球・・・菌を殺す。

・血小板・・・血液を固める。

液体成分は以下の1つだけ。

・血しょう・・・酸素以外の物質を運ぶ。

この血しょうが血管からしみ出たものを組織液といいます。

(3)①

Qは1辺の長さが0.5cmの立方体が8個あります。

1辺が0.5cmの立方体での1つの面の面積は

$$0.5cm×0.5cm=0.25cm^2$$

立方体1つにつき面が6枚あるので表面積は

$$0.25cm^2×6=1.5cm^2$$

立方体8つ分の表面積は

$$1.5cm^2×8=12cm^2$$

よって12cm²となります。

(3)②

柔毛があるのは小腸です。

柔毛があることで、小腸の内側の表面積が大きくなり、効率よく栄養分の吸収を行えるという利点があります。

(4)

刺激を受け取る器官を感覚器官といいます。

以下の5つがあります。

・目・・・・光

・耳・・・・音

・鼻・・・・におい

・舌・・・・味

・皮膚・・・圧力や温度

(6)①

仮説1は「容器の内側が黒ければ、メダカの背中も黒くなる」というもの。

よってア・イのように、容器の内側を黒色にしておけばよいことになります。

(6)②

仮説2は「水面に入る光が強ければ、メダカの背中は淡い茶色になる」というもの。

よってア・ウのように、差し込む光の強さを強くしておけばよいことになります。

(7)

川底は暗い場合が多いです。

そのためメダカの背中は黒色に変化するはず。

すると上空の鳥から見つかりにくくなります。

そのため危険から身を守ることができる可能性が上がります。

大問2の解説

(1)②

仕事の量は次のように求めます。

$$仕事(J)=力(N)×力の向きに動いた距離(m)$$

そのため

$$仕事(J)=300N×1.5m=450J$$

よって450Jが正解となります。

(2)①

この問いにおいて

木片にはたらく浮力の大きさ＝木片の重力の大きさ

となっています。

水を減らしたからといって、木片が浮いた状態ならば、浮力は変わりません。

浮力の大きさは、水中に沈んでいる部分の体積で決まります。

浮力が変わらないということは、沈んでいる部分の体積は変わりません。

したがって木片の水面より上に出ている部分の体積も変わりません。

一方で水圧の大きさは、水面から深さで決まります。

水を減らして水面を下げるということは、放水口の水面からの深さが浅くなるので水圧は小さくなります。

よって放水口から出る水の勢いは弱くなります。

(4)

木片の重さが90Nなので、水そうの底面には

水の重さ＋木片の重さ

がはたらきます。

木片の重さによって水そうの底面にはたらく圧力は

$$圧力=\frac{力}{面積}=\frac{90N}{0.18m^2}=500N/m^2$$

よって木片を取り除くと水そうの底面にはたらく圧力は500Pa減少することになります。

(5)a

落下を始める高さが4倍になったときを考えていますので

表中の「P(高さ10cm)・小球の質量10g」と「R(高さ40cm)・小球の質量10g」

を比較するのがよいでしょう。

このとき小球の速さは

$$2.8m/s÷1.4m/s$=2倍$$

となっています。

高さを2倍、3倍、4倍・・・になると、

速さは√2倍、√3倍、√4倍・・・になります。

(5)b

高さが同じで、小球の質量が3倍になったときを考えていますので

表中の「Q(高さ20cm)・小球の質量10g」と「Q(高さ20cm)・小球の質量30g」

を比較するのが良いでしょう。

このとき木片の移動距離は

$$9.6cm÷3.2cm=3倍$$

となっています。

小球の質量が2倍、3倍、4倍・・・になると

木片の移動距離は2倍、3倍、4倍・・・になります。

(6)

表Ⅰ中のどのデータでもかまいませんので、1つを基準として選びます。

ここでは表のはじめの

P(高さ10cm)・小球の質量10g・木片の移動距離1.6cm・・・①

というデータを使います。

この問いでは

高さ30cm・小球の質量15g

で実験を行います。

高さは①の3倍（＝30cm÷10cm）

小球の質量は1.5倍（＝15g÷10g）

であるので

木片の移動距離は

$$1.6cm×3×1.5=7.2cm$$

となります。

(8)

位置エネルギーと運動エネルギーの和が力学的エネルギーです。

摩擦や空気抵抗がないとき、力学的エネルギーは保存されます。

（これを力学的エネルギーの保存、または力学的エネルギー保存の法則といいます）

位置エネルギーが増加すると、その分運動エネルギーは減少します。

位置エネルギーが減少すると、その分運動エネルギーは増加します。

すなわち位置エネルギーと運動エネルギーは反対の変化をします。

大問3の解説

(3)①

この実験は酸化銅を炭素によって還元しています。

反応のようすは

酸化銅 ＋ 炭素 → 銅 ＋ 二酸化炭素

です。

問題文から

・酸化銅は完全に反応した

・炭素は一部だけ反応し、一部は余った

という条件であることがわかります。

【GさんとI先生の会話1】から

4.00gの酸化銅を完全に反応させると3.20gの銅が生じる

ことがわかります。

「実験2の結果」の文中に「試験管の中に残った物質の質量の合計は3.64gとなった」とあります。

このうち3.20gが銅の質量です。

残りは「反応せず余った炭素」でその質量は

$$余った炭素=3.64g-3.20g=0.44g$$

よって本来より0.44g多く炭素をいれてしまったことになります。

したがってはじめにあった炭素は

$$0.30g+0.44g=0.74g$$

となります。

(3)②

【GさんとI先生の会話1】から

4.00gの酸化銅と炭素0.30gが過不足なく反応して、銅が3.20g生じる

ことがわかっています。

このとき

$$反応前の質量の和=酸化銅+炭素=4.00+0.30=4.30g$$

質量保存の法則を考えると

$$反応後の質量の和=銅+二酸化炭素=4.30g$$

となっているはず。

よって

$$二酸化炭素=4.30-3.20=1.10g$$

発生するはずです。(↓の図)

したがって反応の質量比は↓のようになっています。

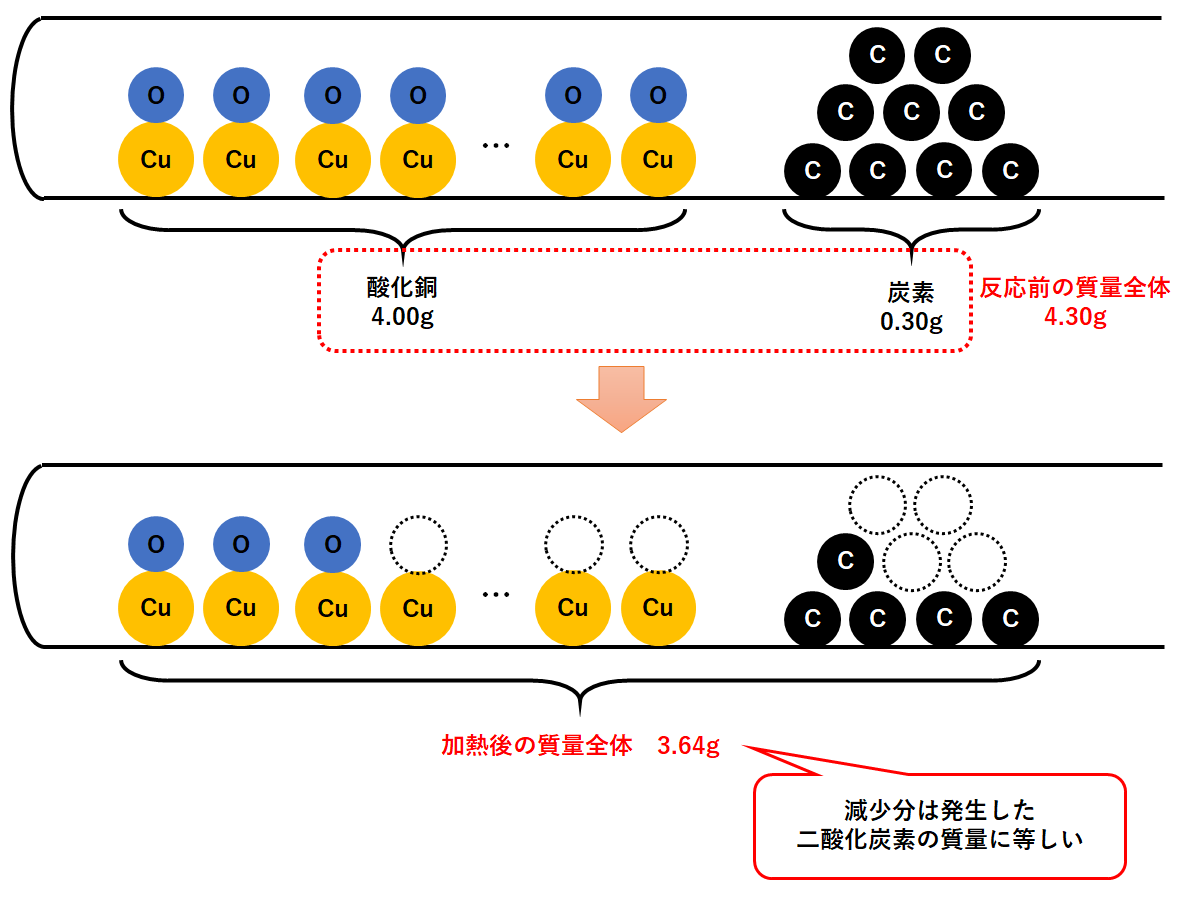
この問いでは

$$反応前の質量の和=酸化銅+炭素=4.00+0.30=4.30g$$

反応後に試験管の中に残った物質の質量の合計が3.64gです。

反応前と反応後で質量が減少しているのは、二酸化炭素が試験管外に出ていったためです。

そのため

$$発生した二酸化炭素=4.30-0.64=0.66g$$

となります。(↓の図)

ここで反応した酸化銅の質量をx(g)とすると

$$4.00:1.10=x(g):0.66g$$

$$x=2.4g$$

したがって、試験管に入れた酸化銅4.00gのうち2.40gが反応したので

$$反応した酸化銅の割合=\frac{2.40}{4.00}×100=60％$$

となります。

(4)

酸化銅と炭素の反応では・・・

酸化銅は銅へと変化した・・・・・・酸化銅が酸素を失った（＝還元）

炭素は二酸化炭素へと変化した・・・炭素が酸素と結びついた（＝酸化）

と還元が起こると同時に酸化も起こっています。

(5)

Gさんの2つ目のセリフより

B、Cが中性・・・・・B、Cは塩化ナトリウム、砂糖

D、Eがアルカリ性・・D、Eが炭酸水素ナトリウム、炭酸ナトリウム

とわかります。

Gさんの3つ目のセリフより

Bは電解質・・・Bが塩化ナトリウム、Cが砂糖

とわかります。

Gさんの4つ目のセリフとI先生の5つ目のセリフより

Eを加熱するとDが生じる・・・Eが炭酸水素ナトリウム、Dが炭酸ナトリウム

残ったAは塩化アンモニウムとなります。

（塩化アンモニウムは酸性ですが、中学では覚える必要はありません。）

大問4の解説

(1)

【Wさんが金星および他の太陽系の惑星について調べたこと】の1つ目に

「金星の大きさや平均密度は地球とほぼ同じ」

とあります。

よって赤道半径や平均密度がほぼ同じfが正解です。

(2)

木星型惑星は赤道半径が大きいですが、密度が小さいのが特徴です。

また基本的に環を持ちます。

ウの選択肢の太陽系外縁天体は、海王星よりも遠くにある天体のこと。

冥王星やエリスという星があてはまります。

(3)

金星の大気の主成分は二酸化炭素です。

二酸化炭素は熱を逃がしにくい性質があり、そのため金星の地表は高温です。

地球上でもこの性質により、二酸化炭素は地球温暖化の原因とされています。

(4)

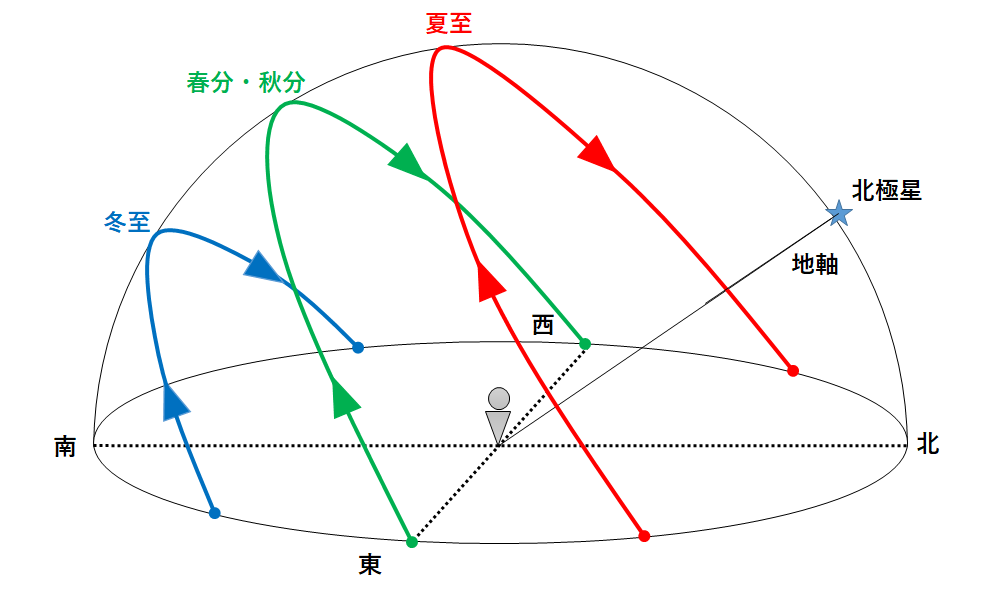
季節による太陽の動きを透明半球に記録すると以下のようになっています。

この問いでは「2月から4月にかけて」の変化を問われているので

日の入りの時刻・・・昼が長くなるので、日の入りは遅くなる。

日の入りの位置・・・真西よりも北寄りに変化する。

となっているウが正解です。

(5)

金星の見え方を理解しておきましょう。

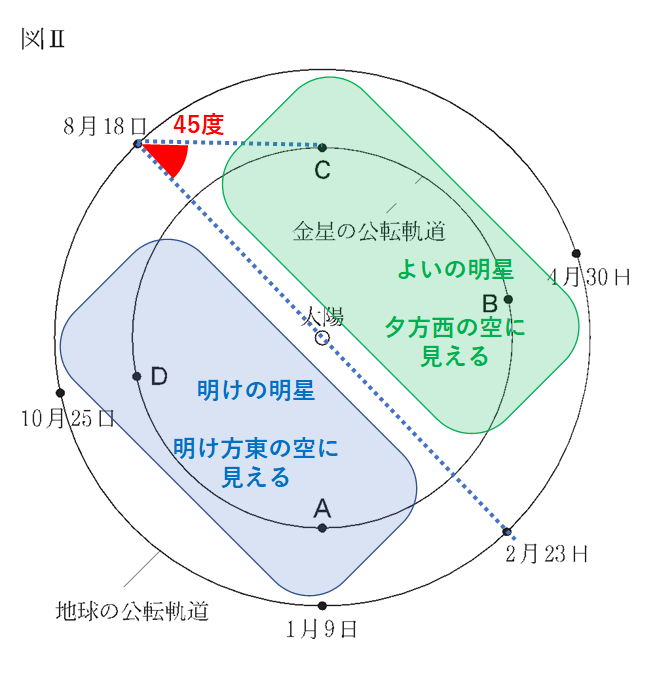
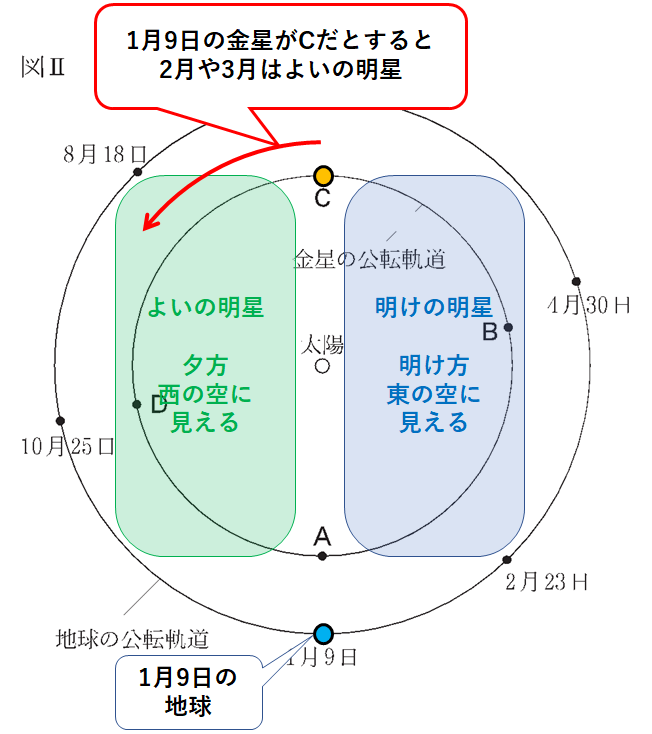
特に金星の位置によって「明けの明星」「よいの明星」として見える時刻、方位が変わります。(↓の図)

さてこの問いについて考えましょう。

【Wさんが金星および他の太陽系の惑星について調べたこと】の最後に

1月9日と10月25日の金星は、地球から見て太陽と同じ方向にある

と書かれています。

このことから図Ⅱ上で

1月9日の金星は、AまたはC

10月25日の金星は、BまたはD

であるとわかります。

【Wさんの天体観測のまとめ】の1つ目に

2月、3月ごろは、日の入り後に金星が観測できた

とあります。（つまりよいの明星）

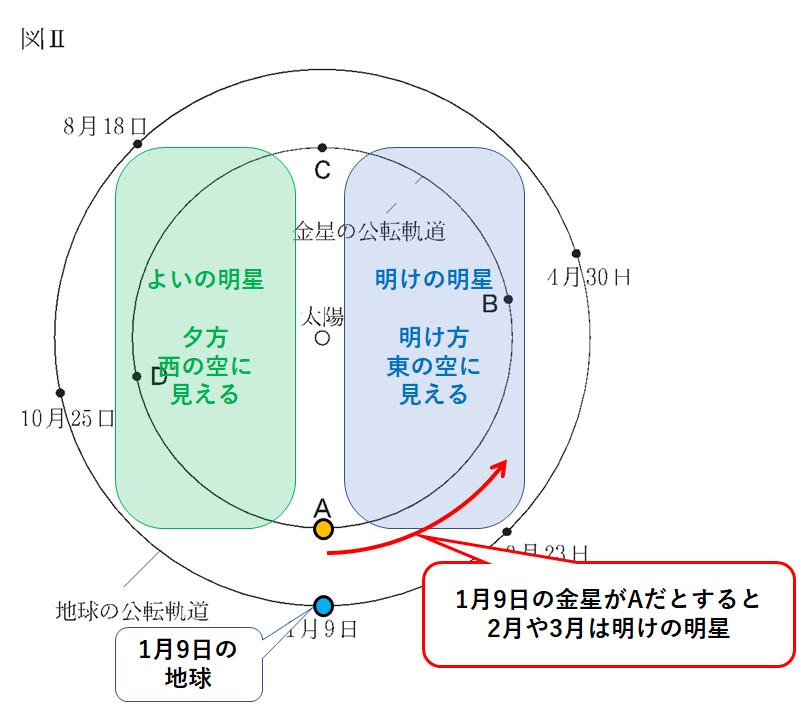
もし1月9日の金星がAの位置ならば

↓のような位置関係になり、明けの明星ということができます。

もし1月9日の金星がCの位置ならば

↓のような位置関係になり、よいの明星ということができます。

したがって1月9日の金星はCの位置にあります。

【Wさんの天体観測のまとめ】の5つ目に

10月までは夕方西の空に、11月からは明け方東の空に金星が見えたとあります。

よって10月25日の金星はDの位置です。(↓の図)

(6)

【Wさんの天体観測のまとめ】の3つ目に

日の入りの時刻に観測すると、地球から見た金星と太陽の角度は8月18日に最も大きかった

とあります。

よって8月18日はよいの明星であること。

そして図ⅡのCの位置に金星があったことがわかります。

この金星はイのような形とわかります。

(7)

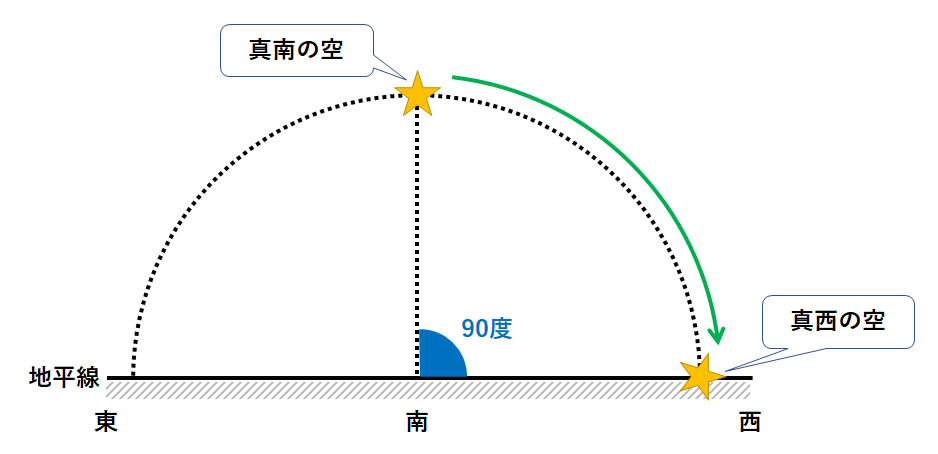
オリオン座のデルタ星が真南に来てから、真西の地平線に沈むまでのようすは↓のようになっています。

90度だけ日周運動をするので、6時間かかります。

（星の日周運動は、1時間で15度ずつ動きます。）

(8)

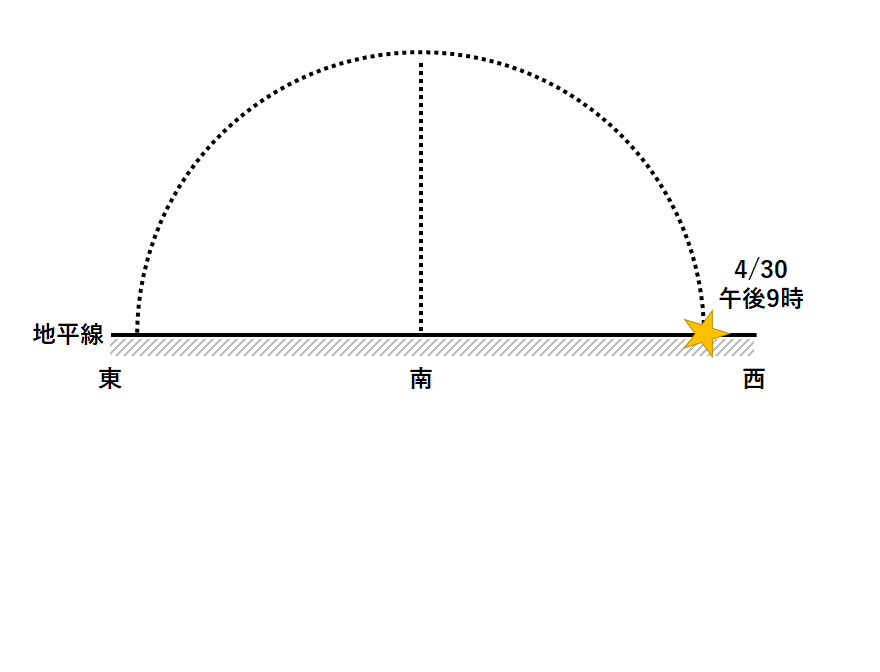
まず4月30日の午後9時に、デルタ星が真西に沈みます。(↓の図)

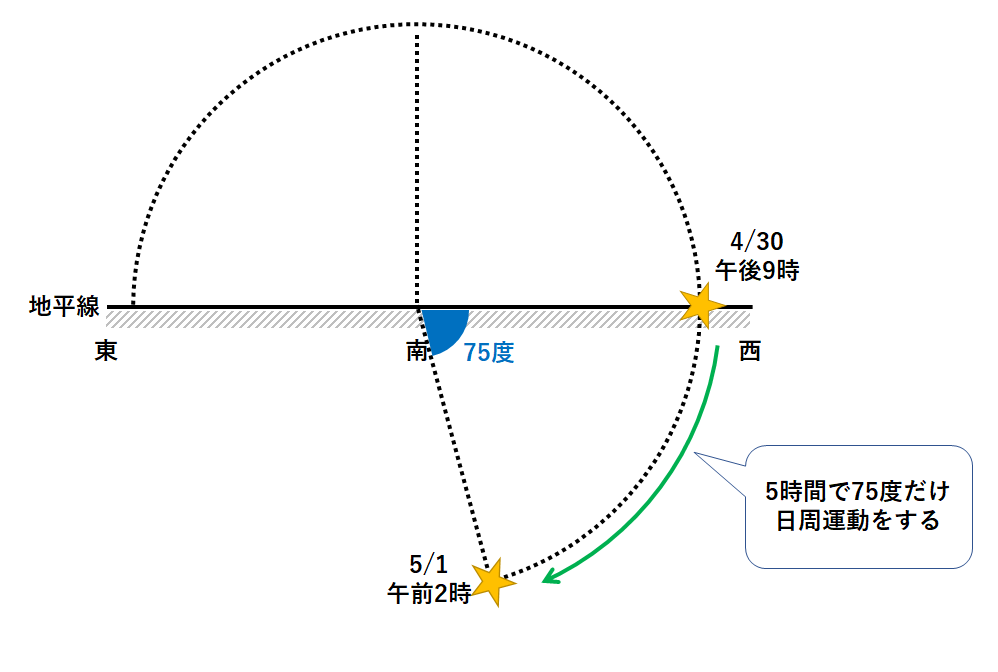
その5時間後（5月1日の午前2時）は、75度だけ日周運動をします。(↓の図)

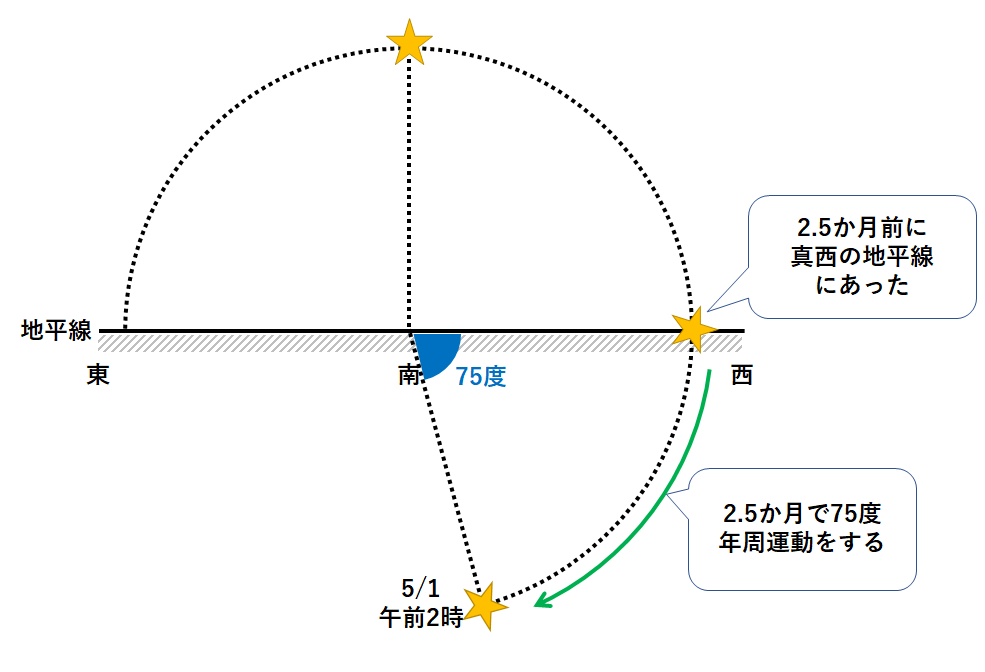
次に年周運動を考えましょう。

5月1日の午前2時に、↓のようにデルタ星があるとすると

Aの位置に見えるのは数か月前ということになります。

年周運動では1ヶ月あたり30度動きます。

よって75度動くには2.5か月（2か月半）かかります。

したがってAの位置に見えるのは2月なかごろの午前2時となります。

大阪府公立高校入試問題（2020年度受験）

posted with ヨメレバ

富士教育出版社 2019年07月

楽天ブックス

Amazon