このページでは「太陽の日周運動」や「透明半球上での太陽の動き」について解説しています。
→【天球】←の内容を理解しておくとよりわかりやすいかと思います。よければ参考に。
このページの動画による解説は↓↓↓
https://youtu.be/undmHxTUc8w
チャンネル登録はこちらから↓↓↓
1.太陽の日周運動
透明半球とは
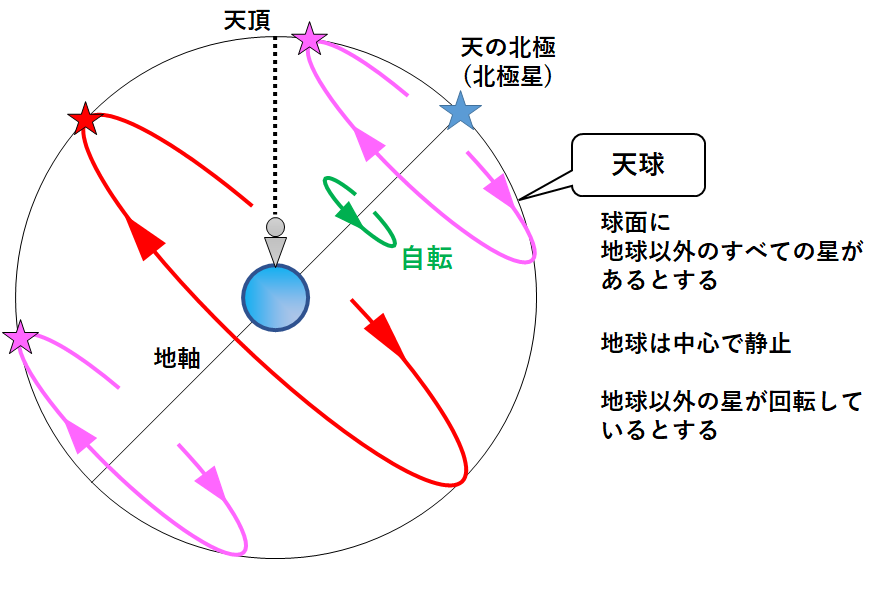
天球では、地球が中心にあり、その他の天体は球面上にあります。(↓の図)
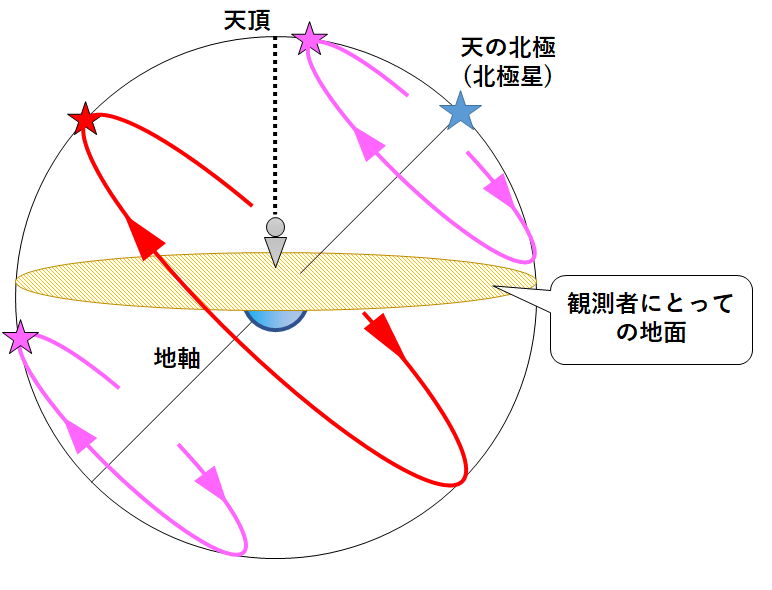
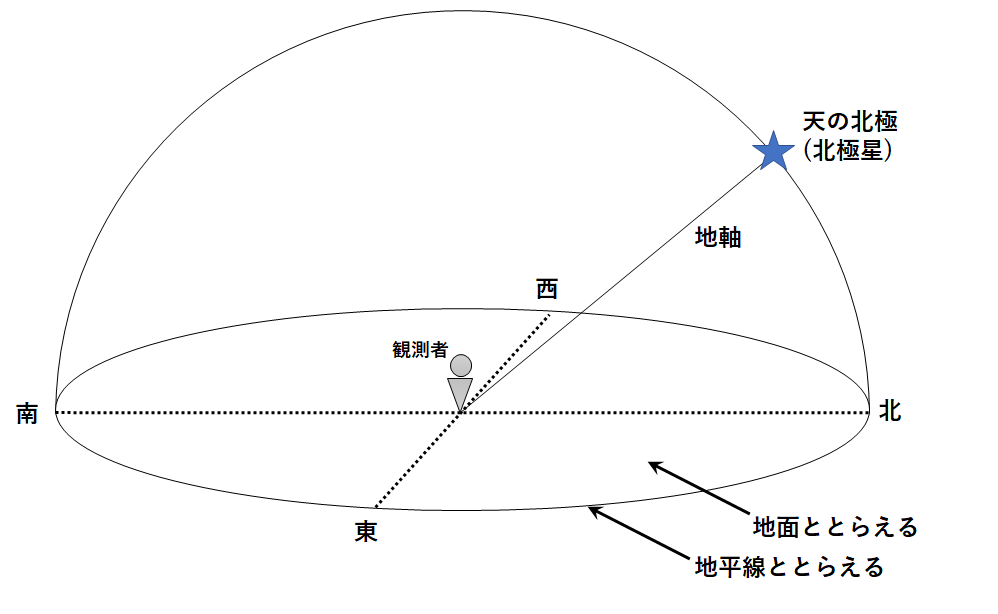
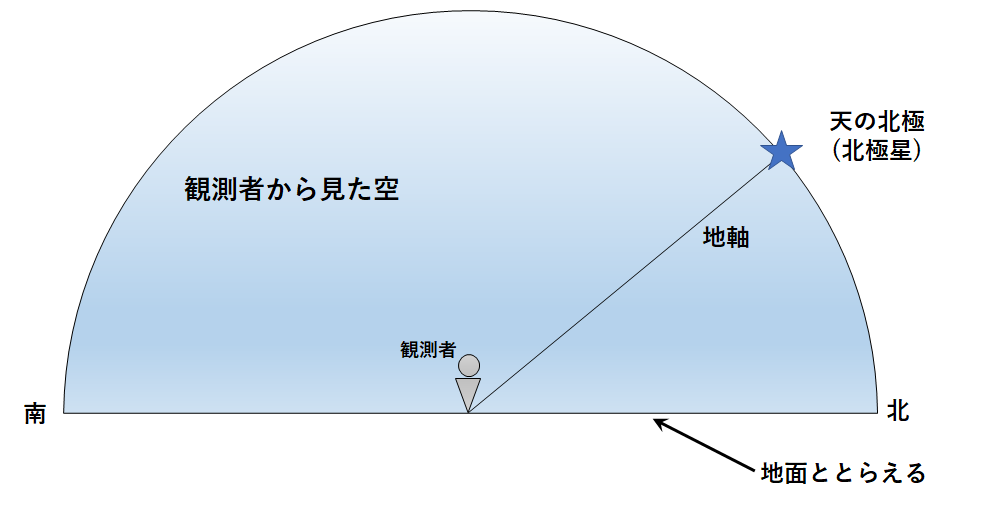
このうち、↓のように観測者の足元を地面ととらえます。
このように天球の上半分(観測者より上側)を考えたものが、透明半球です。
中心に観測者がいると考えています。(↓の図)
横から見たバージョン。
天球上では、地球を除くすべての天体が地軸を中心に回転しています。太陽も同様です。
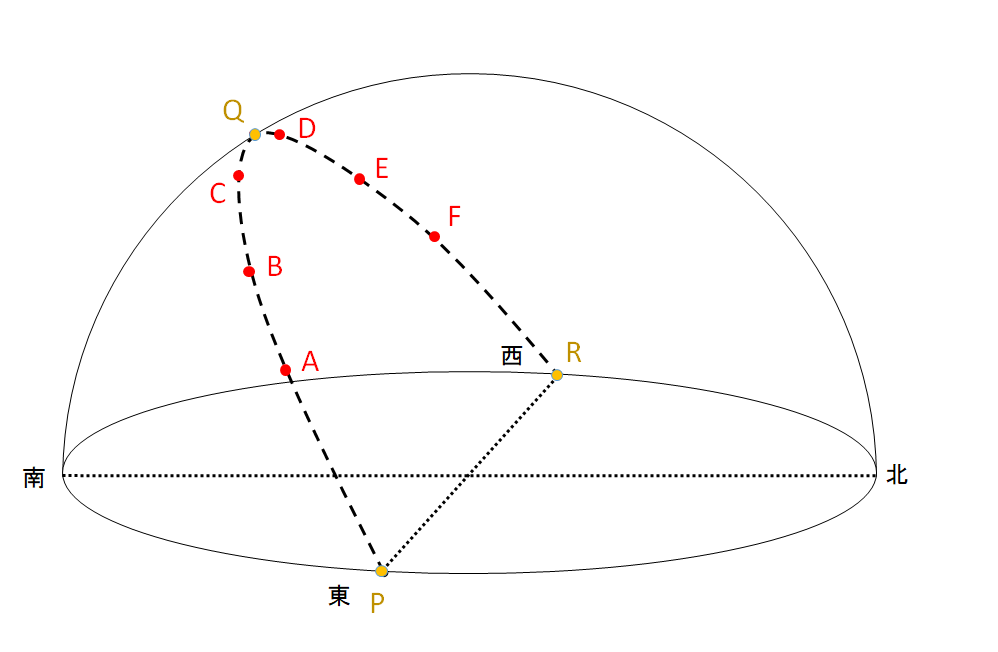
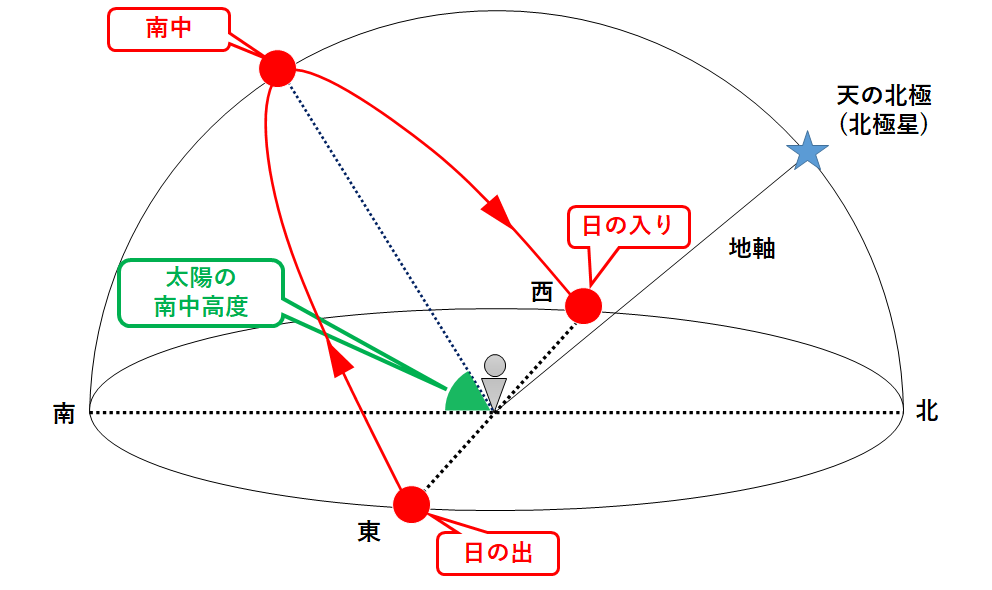
透明半球上で太陽の動きを記すと↓のようになります。
透明半球上での太陽の動きは・・・
①東の空から出る(=日の出)
②南の空で最も高くなる(=南中)
③西の空に沈む(=日の入り)
・・・と動くように見えています。これが太陽の日周運動です。
ここからは日本の兵庫県明石市(東経135度)を中心に考えます。
太陽が天球上を1日に360度(=1時間で15度)回転しているように見える運動。
地球の自転が原因で起こる見かけの動き。
日の出・・・太陽が東の地平線から出ること。
日の入り・・太陽が西の地平線に沈むこと。
昼・・・・・日の出から日の入りまで。
夜・・・・・日の入りから日の出まで。
南中・・・・太陽が南の空にくること。
南中高度・・太陽が南中したときの角度。
2.透明半球をつかった観測
プラスチック製の透明半球を用いて太陽の一定時間ごとの位置を記録していきます。
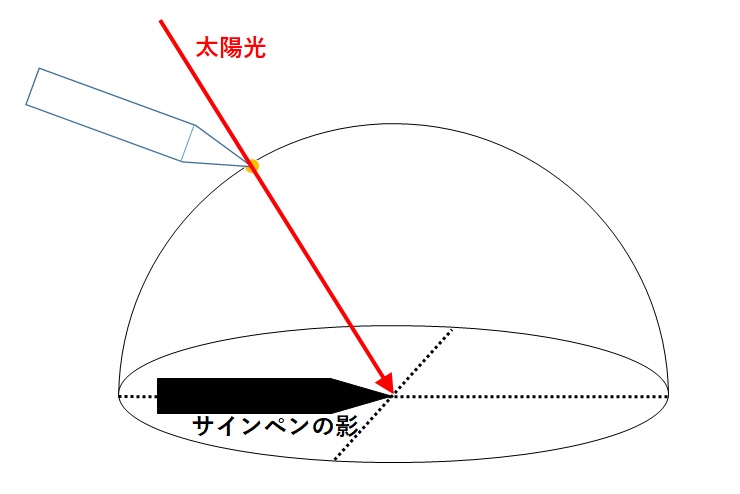
このときサインペンで透明半球に太陽の位置を書き込みます。
サインペンの先端の影が透明半球の中心に重なるように記録します。
ではここで、透明半球の記録を利用した問題を1つ紹介します。
【例題】
A~Fの各点は午前9時から1時間ごとの太陽の位置の記録を表す。
AからBまでの長さは6cmであった。
P・Q・Rは、A~Fの記録から求めた日の出・南中・日の入りの太陽の位置である。
CからQまでの長さは4cm、PからAまでの長さは15cmであった。
(1)BからCまでの長さは何cmか。
(2)この日の太陽の南中時刻を求めよ。
(3)この日の日の出の時刻を求めよ。
(4)この日の日の入りの時刻を求めよ。
(答)
(1)
天球を思い出しましょう。
天球上での太陽は、地軸を中心に1時間に15度ずつ回転しています(ように見える)。
(この動きが太陽の日周運動です。)
1日経つと360度回転します。
地軸を中心とする次のような円を描いているのです。(↓の図)
この円周上を1時間に15度ずつ回転しているので
1時間ごとに太陽が描く弧の長さはすべて同じです。
つまりBからCまでの長さは、AからBまでの長さと等しく6cmとなります。
(2)
南中を表すのはQです。
このQはC(午前11時を表す)から4cmのところにあります。
一方で太陽は1時間で6cmの弧を描くのでした。
ではこの4cmの弧を描くのに x分 かかるとすると
60分:6cm=x分:4cm
これを解いて x=40分
つまりC(午前11時)から40分後が点Qの位置なので
午前11時40分が正解です。
(3)
日の出を表すのはPです。
このPはA(午前9時)から15cmもどったところです。
太陽は1時間で6cmの弧を描くので
15cmの弧を描くのにかかる時間をx分とすると
60分:6cm=x分:15cm
これを解いて x=150分=2時間30分
となります。
つまりPは、A(午前9時)から2時間30分巻き戻した午前6時30分が正解です。
(4)
(1)~(3)より
日の出 から 南中 ・・・ 午前6時30分 から 午前11時40分
とわかっています。
つまり日の出から南中に5時間10分かかっていることがわかります。
南中から日の入りまでも同じく5時間10分かかります。
(南中する時刻は、日の出と日の入りのちょうど真ん中!)
よって日の入りの時刻は、午前11時40分の5時間10分後。
午後4時50分であることがわかります。
※時刻の表記
・午前・午後を付けて表す表し方
・24時制で表す表し方
の2通りあります。
どちらで答えるかは問題文の表記に合わせましょう。
今の例題では「午前」とあるので「午前・午後を付けて表す表し方」で答えを書きます。
POINT!!
・日周運動は1日で360度。1時間あたりで15度。
・透明半球の問題では「時間(分):距離」で比例式をつくる。
3.日本標準時
東経135度(兵庫県明石市)で太陽が南中する時刻を正午とする時刻のこと。
日本の時刻は、東経135度(兵庫県明石市)の地点で太陽が南中した時刻を12:00(正午)としています。
日周運動のペースは、1日(24時間)で360度でした。
よって 1時間あたり15度
または 4分で1度 です。
よって
経度が1度異なる → 南中時刻に4分の差が生じる
ことになります。
例① 東経130°での太陽の南中時刻
東経130度では太陽の南中時刻はどうでしょうか。
東経130度は明石より西です。
太陽の日周運動は東から西への向きなので、明石より南中が遅れて起こることになります。
日周運動のペースは「4分で1度」の動きです。
明石と東経130度の地点では、経度差は5度なので
経度差が5度 ⇒ 南中時刻のずれは20分
よって東経130度では12時20分に太陽が南中します。
例② 東経137°での太陽の南中時刻
東経137度では太陽の南中時刻はどうでしょうか。
東経137度は明石より東です。
太陽の日周運動は東から西への向きなので、明石より南中がはやく起こることになります。
日周運動のペースは「4分で1度」。
明石と東経137度の地点では経度差が2度。(137ー135=2度)
経度差が2度 ⇒ 南中時刻のずれが8分
よって東経137度では11時52分に太陽が南中します。
POINT!!
・東経が1度大きくなる→南中が4分はやくなる。
・東経が1度小さくなる→南中が4分おそくなる。
※経度の基準(経度が0度の地点)はイギリスのロンドンです。
※ロンドンから東に行くと「東経」、西に行くと「西経」となります。
※ロンドンでの太陽の南中を基準とする時刻を「世界標準時」といいます。
※実は日の出や日の入りの時刻のずれは経度だけではなく、季節の影響を受けます。




コメント(承認された場合のみ表示されます)
問題で透明半球を1時間に移動する距離は春分と秋分が最大で夏至と冬至が最小になるとあったのですがこれは1時間15度移動するということを保っていても移動距離が長い春分や冬至は移動距離が長くなるということですか?
みーたん様
コメントありがとうございます。
ご質問の件ですが、おっしゃる通り
「透明半球上での1時間の移動距離は、春分秋分が最も長く、夏至冬至が最も短い」です。
透明半球上での各季節の太陽の記録は↓の図のようになります。
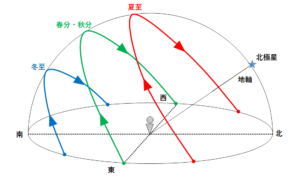
これを天球全体にしてみると↓のようになっています。
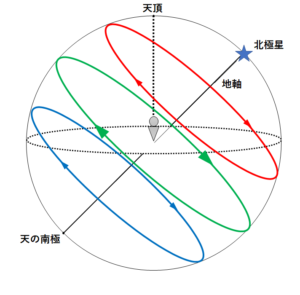
真横から見ると↓の図のように。
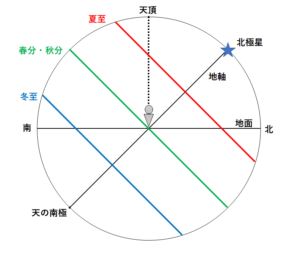
地軸と春分秋分・夏至・冬至の日周運動の道筋を取り出すと↓のようになっています。
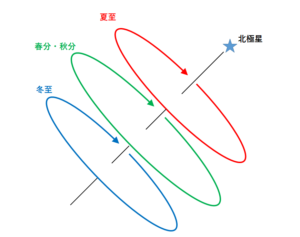
緑・赤・青の3枚の円盤があるようなイメージです。
今までの図から考えて、この円盤のサイズは緑が最も大きく、赤と青が最も小さいのはわかりますか?
この円盤のふちを太陽が1時間で15度ずつ動いていくのですが、
春分・秋分がもっとも大きな円盤のふちを動くため、1時間当たりの移動距離が大きく
(1時間あたりに描く弧が最も大きいということ)
夏至・冬至がもっとも小さな円盤のふちを動くため、1時間当たりの移動距離が小さい
(1時間あたりに描く弧が最も小さいということ)
ということになるのです。
そのため「透明半球上での1時間の移動距離」を比べると、春分秋分が最も長く、夏至冬至が最も短いのです。
わかりにくければ補足するので言ってくださいね。
はじめ、天球上の太陽の軌道が半円だと思って問題を解いてしまったため間違えてしまいました。昼の長さが短いので線分PRは円の中心よりも少し南側を通っているということでしょうか?
しがかて様
コメントありがとうございます。
>昼の長さが短いので線分PRは円の中心よりも少し南側を通っているということ
そうですね。ちょっと図が悪かったです。
図を修正したので、よければ見てみてください。
例題の透明半球ですが、図では太陽が真東から昇り真西に沈んでいるように見えます。これだと春分または秋分で、昼と夜は同じ長さになるので、日の出から日の入りまでが5時間10分×2で10時間20分になるという感覚がおかしいと混乱するように感じるのですが、、
can様
コメントありがとうございます。
ご指摘の通りです。
混乱を招くので、図を差し替えました。ご指摘ありがとうございます。
とてもわかりやすい説明ありがとうございます。
1点質問があります。
地軸の延長線上に北極星があり、北極星の高さは観測地点の緯度と一緒、ということを説明されているのですが、「地軸は公転面に対して23.4°傾いている」という知識とこんがらがってしまっています。天球モデルで見ると、「23.4°傾いて回っている」という地軸の傾きから考えてしまうと、「北極星の角度は(90°-23.4=66.6°では?)」と思ってしまいます。でも、この考え方が間違いなのもわかっています(北極星の高さが緯度であるという動画も拝見し、理解しました)。こちらのホームページ含め、いくつかのサイトを見たのですが、「地軸の傾きが23.4°」の話と、天体モデルの北極星を中心に傾いて太陽は日周運動している(そして、その中心となる北極星の高さは23.4でもなければ66.6°でもなく、緯度(日本の場合、35°))の部分をどう理解すればよろしいでしょうか。
みけねこ様
コメントありがとうございます。
またご質問いただいていたのに返信が遅くなり大変申し訳ありません。
地軸の傾きは北極星を見上げる高度とは無関係です。
みけねこ様のおっしゃっているのは「季節によって北極星の高度は変わるのではないか」ということでしょうか。