このページでは合成抵抗の公式がどのように導かれるかを解説しています。
動画による解説は↓↓↓
チャンネル登録はこちら↓↓↓
合成抵抗の使い方などは→【合成抵抗の使い方】←を参考に。
やや発展的な内容です。
1.合成抵抗の求め方
このページではなぜ合成抵抗が↑のようにして求められるのか解説します。
2.合成抵抗の公式を導く
直列回路の場合
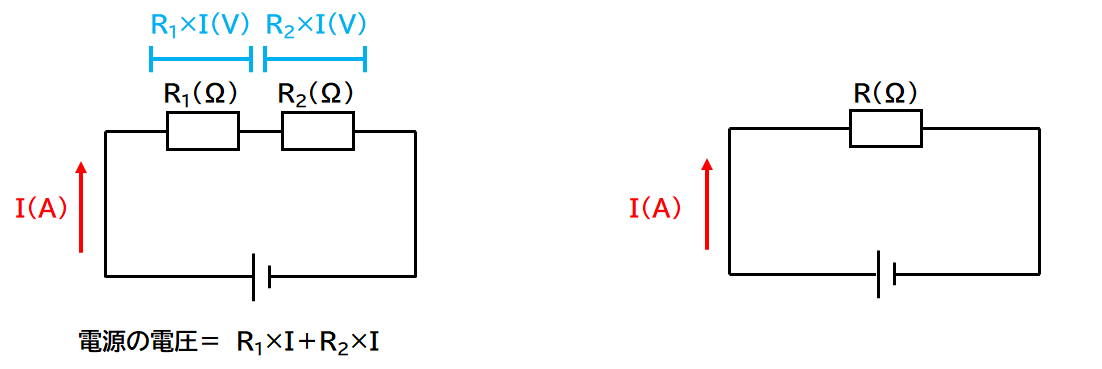
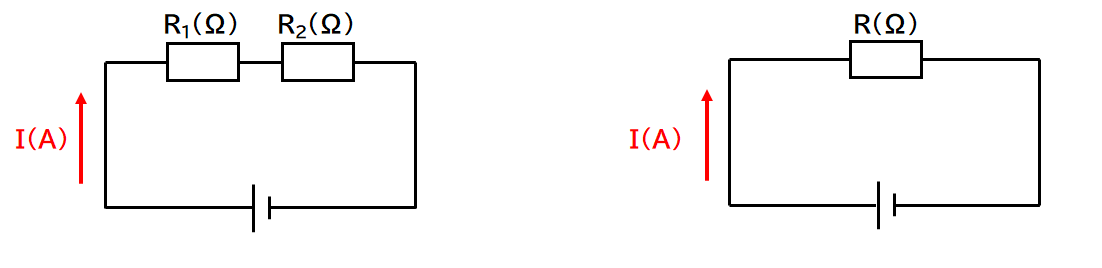
↓の左図の2つの抵抗器をまとめて(合成して)、右図のような回路にします。
したがって左右の電源の電圧は同じです。また回路全体に流れる電流も同じです。
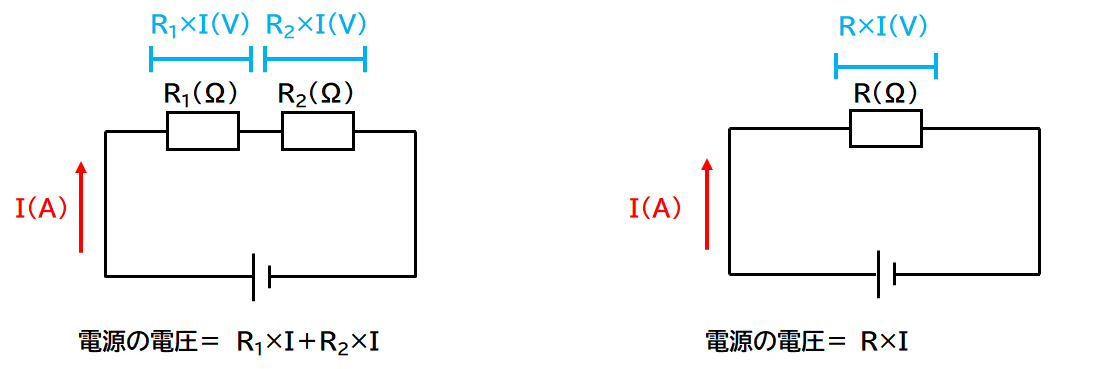
そこで回路全体に流れる電流をI(A)とします。(↓の図)
オームの法則よりR1(Ω)の抵抗器に加わる電圧は
$$電圧=抵抗×電流=R_1(Ω)×I(A)=R_1I(V)$$
R2(Ω)の抵抗器に加わる電圧は
$$電圧=抵抗×電流=R_2(Ω)×I(A)=R_2I(V)$$
よって左の回路の電源電圧は
$$R_1I+R_2I(V)・・・①$$
と表されます。(↓の図)
一方で右の回路のR(Ω)の抵抗器に加わる電圧は
$$電圧=抵抗×電流=R(Ω)×I(A)=RI(V)$$
よって右の回路の電源電圧も
$$RI(V)・・・②$$
となります。(↓の図)
①と②は等しいので
$$R_1I+R_2I=RI$$
この式の両辺をIで割って(Iを消去)
$$R_1+R_2=R$$
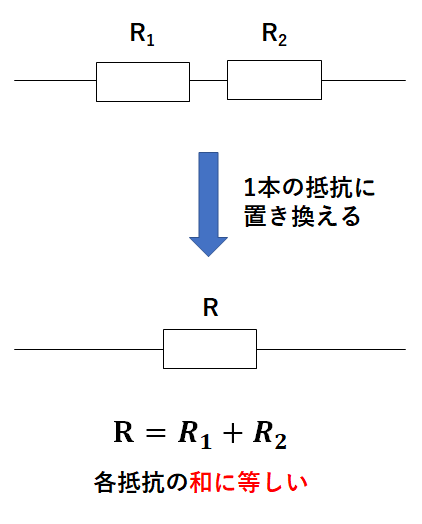
したがって左の回路の抵抗の和=右の回路の抵抗となります。
すなわち直列の合成抵抗=各抵抗器の和となるといえます。
並列の場合
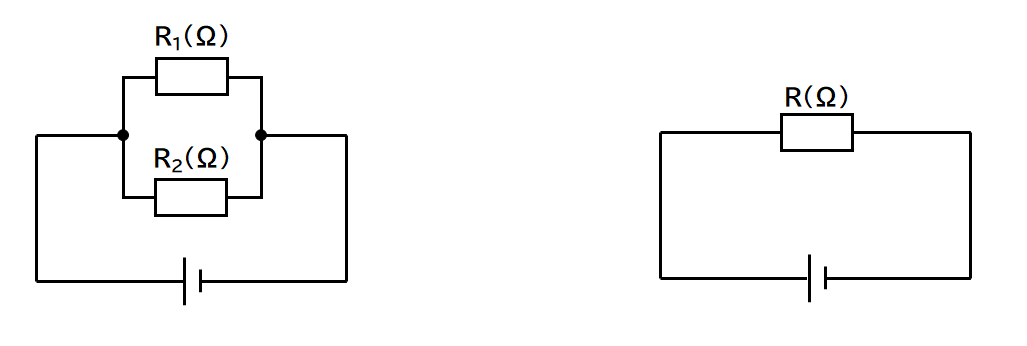
↓の左図の2つの抵抗器をまとめて(合成して)、右図のような回路にします。
したがって左右の電源の電圧は同じです。また回路全体に流れる電流も同じです。
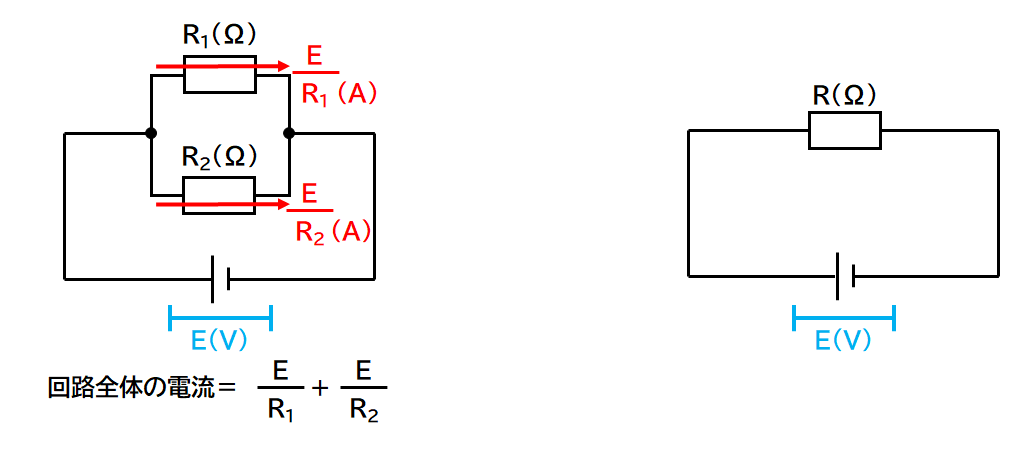
そこで電源の電圧をE(V)とします。(↓の図)
オームの法則より、左の回路のR1(Ω)の抵抗器に流れる電流は
$$電流=\frac{電圧}{抵抗}=\frac{E}{R_1}(A)$$
左の回路のR2(Ω)の抵抗器に流れる電流は
$$電流=\frac{電圧}{抵抗}=\frac{E}{R_2}(A)$$
したがって回路全体に流れる電流は
$$\frac{E}{R_1}+\frac{E}{R_2}(A)・・・①$$
となります。(↓の図)
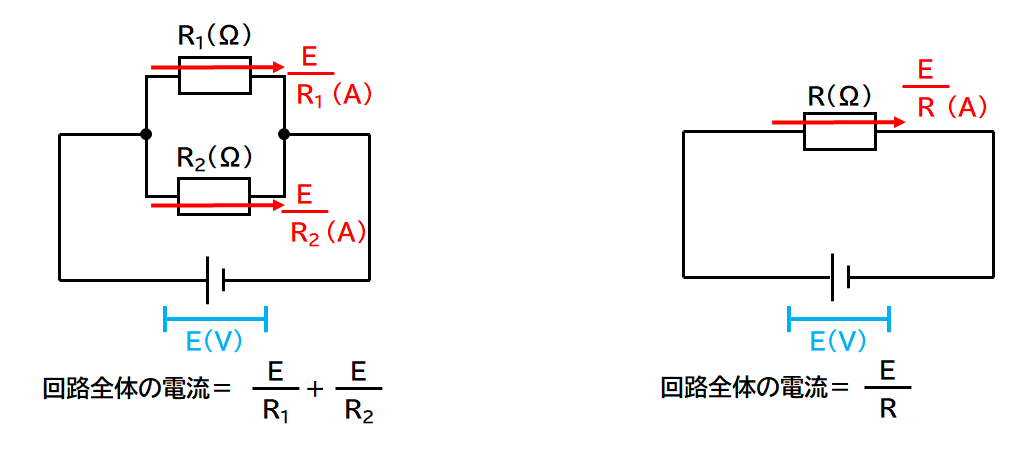
一方で右の回路のR(Ω)の抵抗器に流れる電流は
$$電流=\frac{電圧}{抵抗}=\frac{E}{R}(A)・・・②$$
となります。(↓の図)
①と②は等しいので
$$\frac{E}{R_1}+\frac{E}{R_2}=\frac{E}{R}$$
両辺をEで割って
$$\frac{1}{R_1}+\frac{1}{R_2}=\frac{1}{R}$$
左辺をR1R2に通分して
$$\frac{R_1+R_2}{R_1R_2}=\frac{1}{R}$$
両辺の分母と分子を入れかえて
$$\frac{R_1R_2}{R_1+R_2}=R$$
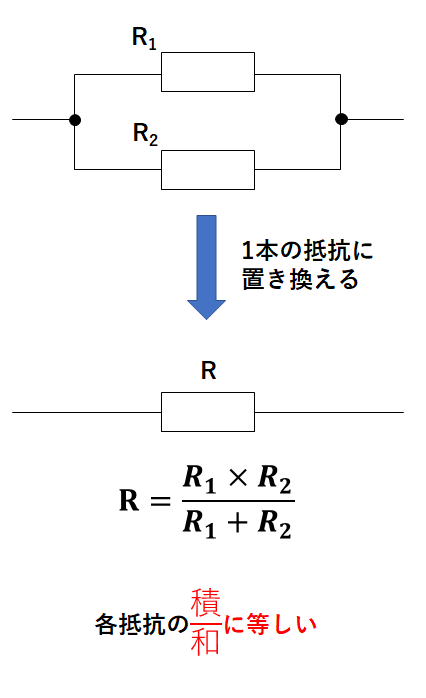
この式は
$$R=\frac{R_1とR_2の積}{R_1とR_2の和}$$
となっています。
以上にようにして合成抵抗の公式は求めることができます。



コメント(承認された場合のみ表示されます)