光の速さをはじめて実験によって測定したのは、フランスのアルマン・フィゾーでした。
ここではフィゾーがどのように光の速さを測定したのか紹介していきます。
高校入試問題としてはラサール高校や東大寺学園高校で近い設定の問題が出題されました。
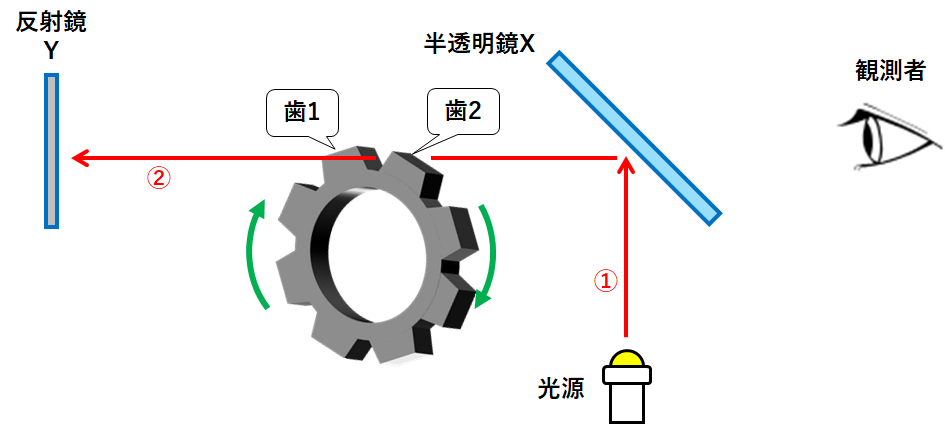
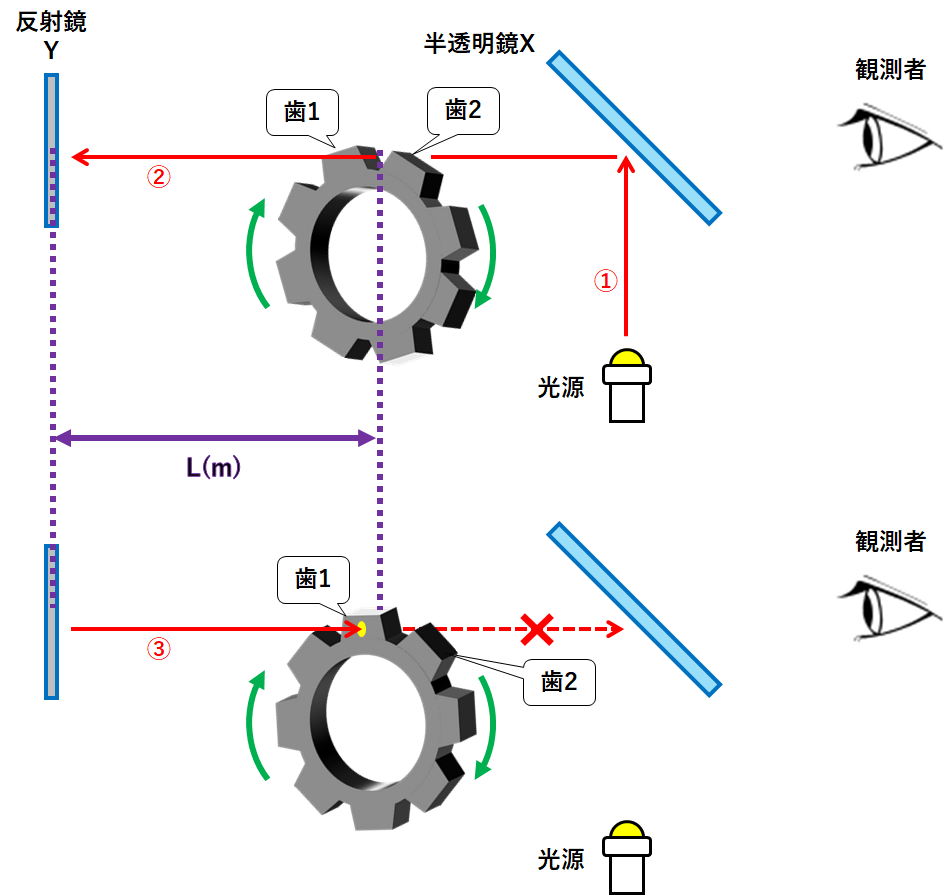
フィゾーは↓のような装置を利用しました。
半透明鏡とは「光の半分は反射する・残り半分は鏡を通り抜ける」という鏡です。
光の進み方は以下のようになっています。
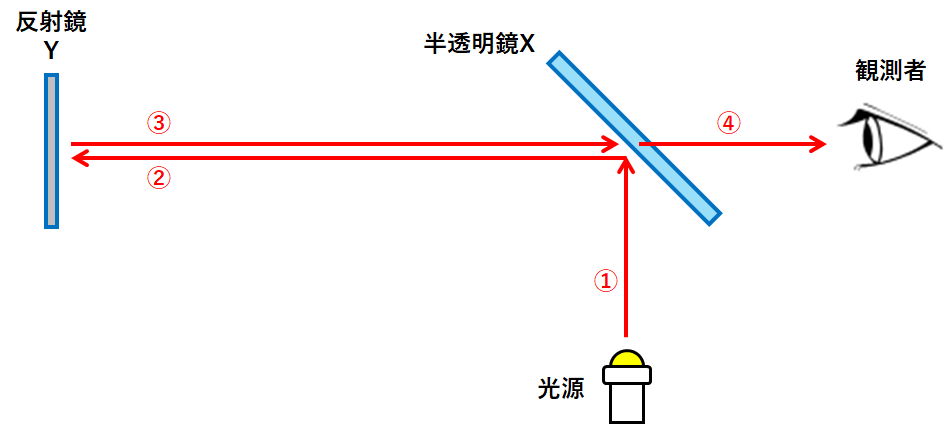
①光源から半透明鏡Xへ
②半透明鏡Xで反射した光が反射鏡Yへ
③反射鏡Yで反射した光が半透明鏡Xへ
④③のうち一部の光が半透明鏡Xを通り抜けて観測者へ
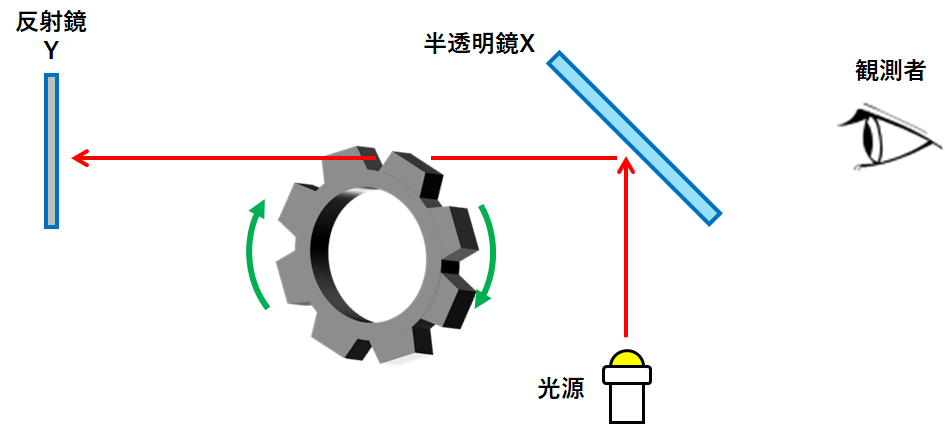
ここで回転する歯車を置きます。(↓の図)
そして光源から光を出発させます。
このとき②の光がちょうど歯車の歯1と歯2の間を通り抜けたとします。(↓の図)
その後、②の光は反射鏡Yで反射します。つまり③の光です。
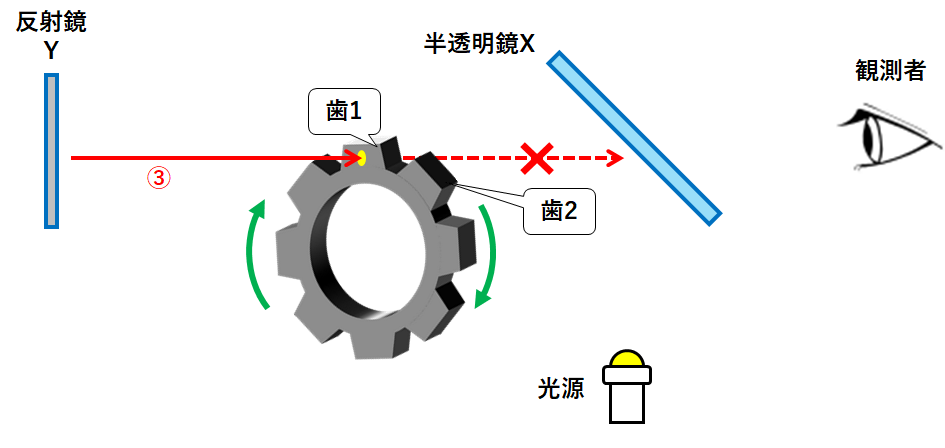
③の光が歯車までやってきたとき、歯車は先ほどより少し回転しています。
歯車の回転速度によっては↓のように歯1に当たります。
観測者からすると、④の光を観測できません。
歯車の回転速度がわかっていれば、
(ⅰ) ②の光が歯1と歯2の間を通り抜けてから③の光が歯1にあたるまでの時間
が求められます。
また歯車と反射鏡Yまでの距離がわかれば、
(ⅱ) ②の光が歯1と歯2の間を通り抜けてから③の光が歯1にあたるまで移動した距離
が求められます。
これを利用すると光の速さが計算できる、というわけです。
では実際に光の速さの計算を考えてみましょう。
歯車から反射鏡Yまでの距離をL(m)とします。
また歯車の歯の数をN個(図は歯の数が8個ですが)、歯車の1秒当たりの回転回数をn回とします。
まず (ⅰ)②の光が歯1と歯2の間を通り抜けてから③の光が歯1にあたるまでの時間 を考えます。
図のように歯の数が8個の場合、歯と歯のすき間の数も8個です。
↓のように歯1と歯2の間を通り抜けた光が歯1にあたるまでの時間は16分の1回転に等しいです。
歯車の1秒当たりの回転数がn回ということは
$$歯車が1回転する時間=\frac{1}{n}秒$$
であるので
$$歯車が16分の1回転する時間=\frac{1}{n}×\frac{1}{16}=\frac{1}{16n}秒$$
となります。
いま歯の数がN個と考えているので、歯と歯のすき間の数は2N個。
歯1と歯2の間を通り抜けた光が歯1にあたるまでの時間は2N分の1回転に等しいので
$$歯車が2N分の1回転する時間=\frac{1}{n}×\frac{1}{2N}=\frac{1}{2nN}秒$$
となります。
次に (ⅱ)②の光が歯1と歯2の間を通り抜けてから③の光が歯1にあたるまで移動した距離 を考えます。
歯車から反射鏡Yまでの距離がL(m)なので
$$光が歯1と歯2の間を通り抜けてから歯1にあたるまで移動した距離=2L(m)$$
となります。(往復したので2倍するだけ)
したがって光の速さは
$$光の速さ=(ⅱ)の距離÷(ⅰ)の時間$$
$$=2L(m)÷\frac{1}{2nN}秒$$
$$=4nNL(m/s)$$
となります。
当時のフィゾーの実験では、
歯車の1秒当たりの回転回数を12.6回、歯の数を720個、歯車と反射鏡Yまでの距離を8633mとして実験しました。
その結果、光の速さ=3 1300 0000m/sという値を得ました。
実際の光の速さ(真空中)2 9979 2458 m/sであるので、やや差はありますが、当時としては精度の高い値が計算できました。




コメント(承認された場合のみ表示されます)