このページでは2018年度の愛知県立入試の問題Bグループを解説しています。(理科のみ)
問題・模範解答はこちら↓↓
http://www.zenkenmoshi.jp/nyushi/nyushi.html
↓↓佐鳴予備校さんのページにも掲載されています。
https://www.sanaru-net.com/entrance-aichi/sokuhou_b/
大問1の解説
(1)
実験①と実験②で異なる点は
・木片の位置を右側にした
・強くはじいた
という2点です。
木片の位置を右側にした=はじく弦が長くなった
ということ。
①より音は高くなる・振動数は多くなるという変化があります。
強くはじいた=大きな音が鳴る
ということ。
①より振幅が大きくなるという変化があります。
そのため実験②のオシロスコープの波形はaとなります。
また実験③では
・木片の位置は①と同じ
・弦の張りは①よりも強い
・はじく強さは②と同じ
つまり①と比べると
弦の張りは①よりも強い=①よりも高い音が鳴る
ということ。
①より振動数は多くなります。
はじく強さは②と同じ=①よりも大きな音が鳴る
ということ。
①よりも振幅が大きいという変化があります。
そのため実験③でのオシロスコープの波形はcとなります。
(2)
図中のAは肝臓、Bはじん臓です。
肝臓では有害なアンモニアを尿素につくりかえています。
じん臓では運ばれてきた尿素を血液からこしとるはたらきがあります。
よってエの選択肢が正解です。
大問2の解説
(1)
ソラマメのXの部分(食用の部分)は種子にあたります。
種子のまわりにあるものを果実といいます。
ソラマメでは“さや”の部分が果実にあたります。
さやの部分を食べることはあまりありませんね。
一方、カキ(図7)やリンゴなどは
種子(図7のM)を食べることはありませんが、果実の部分(図7のN)を食用としています。
このように植物によって、どの部分が果実なのかが紛らわしいので気を付けましょう。
(2)
オの選択肢が誤った内容が書かれています。
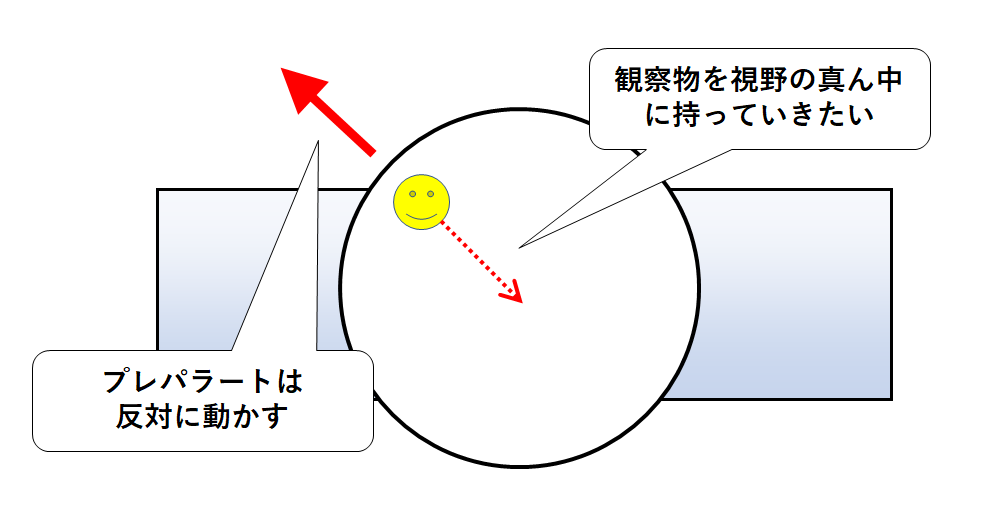
視野の左上に見えたものを中央に移動させるには、プレパラートを左上に動かさなければなりません。
(↓の図)
これは顕微鏡で見える像は上下左右反対に見えていることが原因です。
そのため、プレパラートを実際に動かす向きは
動かしたい方向と逆向き
と覚えておくとよいでしょう。
(4)
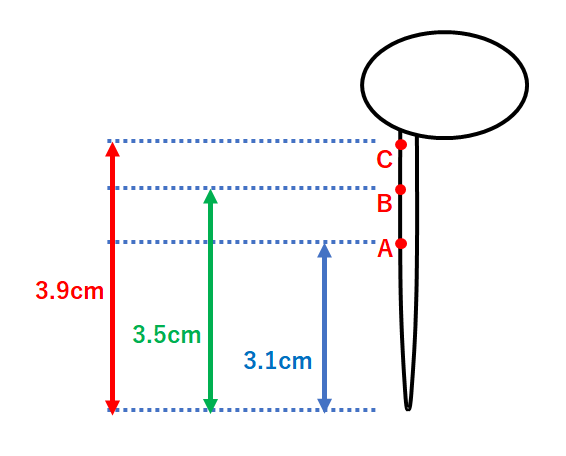
実験1では、根の先端から4mm間隔となるようにa・b・cの印をつけています。
ここで表1に注目しましょう。
先端からaまでは3.1cm
先端からbまでは3.5cm
先端からcまでは3.9cm
という記録です。(↓の図)
よって
先端~aまでは3.1cm
a~bまでは3.5-3.1=0.4cm=4mm
b~cまでは3.9-3.5=0.4cm=4mm
したがって
a~bの部分とb~cの部分はまったく伸びていません。
一方で先端~aまではよくのびていることがわかります。(4mm→3.1cm)
よって根は先端部分でよくのびていることがわかります。
また実験2では細胞の数を数えています。
表2に注目すると
Ⅰの部分は細胞が150個と、ほかの部分よりもかなり細胞が多いことがわかります。
ということは、1つ1つの細胞の大きさが非常に小さいために、一度にたくさんの細胞が観察できたのだと考えられます。
これらのことを総合すると
根の成長では、細胞分裂によって細胞の数が増えて、1つ1つの細胞が大きくなっていることがわかります。
(非常によく出題されることなので、覚えておきましょう)
大問3の解説
(1)
塩化銅水溶液の電気分解では
陽極(+極側):塩素の気体 陰極(-極側):銅の固体
が生じます。
※ちなみに塩酸の電気分解では
陽極(+極側):塩素の気体 陰極(-極側):水素の気体
が生じます。
※水(水酸化ナトリウム水溶液)の電気分解では
陽極(+極側):酸素の気体 陰極(-極側):水素の気体
が生じます。
(2)
表1に注目。
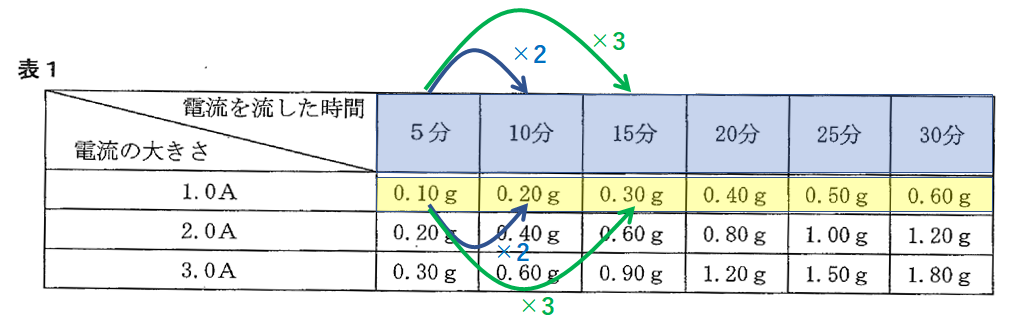
電流の大きさが1.0Aのとき、
電流を流した時間に比例して、発生する銅の質量が増えています。(↓の図)
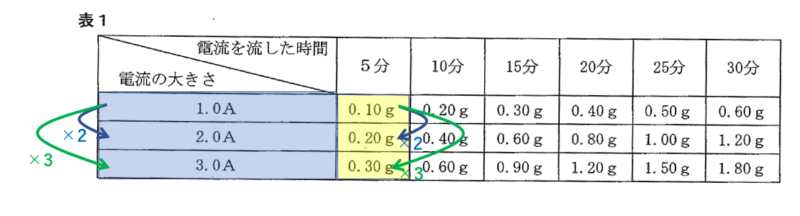
また電流を流した時間が5分間のとき、
流した電流の強さに比例して、発生する銅の質量が増えています。(↓の図)
したがって
発生する銅の質量は、時間に比例し、電流の強さにも比例する
ことがわかります。
表1より
5分間・1.0Aのとき 発生する銅が0.10gなので
17分間・1.0Aならば
$$生じる銅=0.10g×\frac{17}{5}=0.34g$$
となります。(時間が17/5倍)
そして17分間・2.5Aならば
$$生じる銅=0.34g×2.5=0.85g$$
となります。(電流が2.5倍)
0.85gが正解です。
(3)
実験2の④では
Ba(OH)2 + H2SO4 → BaSO4 + 2H2O
という中和反応が起こっています。
白い沈殿の正体はBaSO4 硫酸バリウムです。
(4)
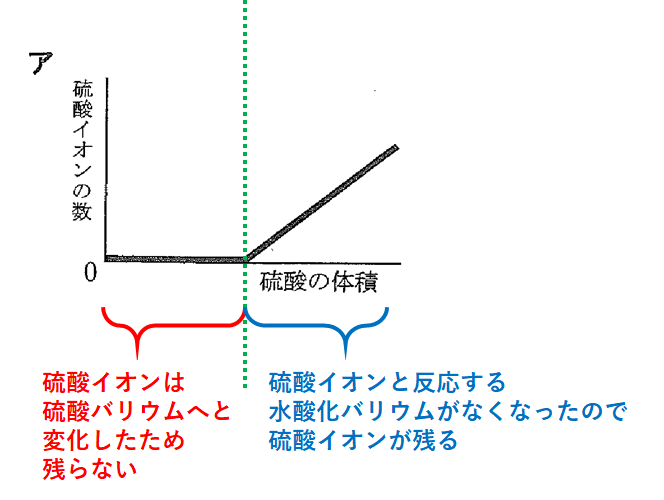
この問いでは
水酸化バリウム水溶液の入ったビーカーaに、硫酸を少しずつ加えていくという操作をしています。
▼少しの硫酸を加えたとき・・・
硫酸イオンはバリウムイオンと反応し、硫酸バリウムとなります。
硫酸イオンは、すぐに硫酸バリウムへと変化するので、ビーカーには残りません。
▼たくさんの硫酸を加えたとき・・・
硫酸イオンと反応するバリウムイオンにも限りがあります。
あまりに多くの硫酸イオンが入れば、硫酸イオンが余ってしまいます。
この場合はビーカーに硫酸イオンが残った状態になります。
以上のことを表すグラフはアのみです。(↓の図)
大問4の解説
(1)
オームの法則より
$$\frac{5V}{2Ω}=2.5A$$
となります。
(2)
実験1では
電熱線に電流を流すことで熱を発生させ、カップ内の水の温度を上げようとしています。
電熱線から発生する熱の量(熱量)は
$$熱量(J)=電力(W)×時間(秒)$$
で求められます。
電力は
$$電力(W)=電流(A)×電圧(V))$$
で求められます。
そのため、水の上昇温度を考えるためには、必ず電力を求めておかなければなりません。
この実験では、2.0Ω・5.0Ω・10.0Ωの3つの電熱線を用いています。
それぞれの場合の電力を求めてみましょう。
▼2.0Ωの電熱線を用いたとき・・・
電圧計が5.0Vであるので
オームの法則より
$$電流(A)=\frac{5.0V}{2.0Ω}=2.5A$$
電力の公式より
$$電力(W)=2.5A×5.0V=12.5W$$
▼5.0Ωの電熱線を用いたとき・・・
電圧計が5.0Vであるので
オームの法則より
$$電流(A)=\frac{5.0V}{5.0Ω}=1A$$
電力の公式より
$$電力(W)=1A×5.0V=5W$$
▼10.0Ωの電熱線を用いたとき・・・
電圧計が5.0Vであるので
オームの法則より
$$電流(A)=\frac{5.0V}{10.0Ω}=0.5A$$
電力の公式より
$$電力(W)=0.5A×5.0V=2.5W$$
以上のように電力は
2.0Ωの電熱線のとき 12.5W
5.0Ωの電熱線のとき 5W
10.0Ωの電熱線のとき 2.5W
です。
これを比にすると
$$(2.0Ωを用いたとき):(5.0Ωを用いたとき): (10.0Ωを用いたとき)=12.5:5:2.5=5:2:1$$
です。
そのため
同じ時間だけ電流を流したときの発熱量の比も
$$(2.0Ωを用いたとき):(5.0Ωを用いたとき): (10.0Ωを用いたとき)=5:2:1$$
となり、
同じ時間だけ電流を流したときの上昇温度の比も
$$(2.0Ωを用いたとき):(5.0Ωを用いたとき): (10.0Ωを用いたとき)=5:2:1$$
となります。
5.0Ωのを用いたときの水の上昇温度は、10.0Ωを用いたときの2倍です。
よって書くべきグラフは↓のようになります。
(4)
▼空欄Ⅰ
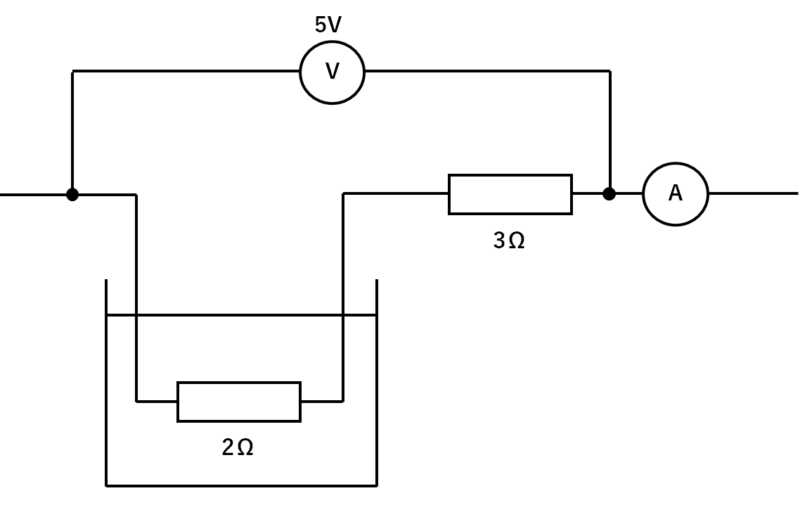
実験2の回路の様子を回路図で表すと↓のようになっています。
ここから
$$回路に流れる電流=\frac{5.0V}{2Ω+3Ω}=1A$$
$$2Ωの電熱線に加わる電圧=2Ω×1A=2V$$
$$2Ωの電熱線での電力=2V×1A=2W$$
となります。
よってこの電力は実験1で2.0Ωの電熱線を用いたときに比べて
$$2W÷12.5W=0.16倍$$
です。
空欄Ⅰの答えは0.16倍です。
▼空欄Ⅱ
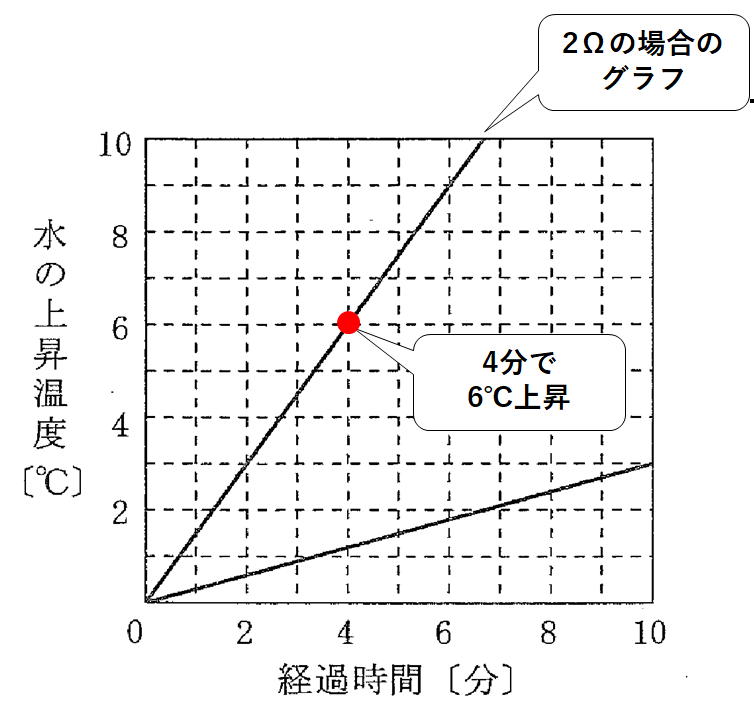
実験1で2.0Ωの電熱線を用いたときの水の上昇温度を調べます。(↓の図)
4分で水温が6℃上昇しています。
5分ならば7.5℃上昇しているはずです。
実験2での電力は
実験1で2.0Ωの電熱線を用いたときの0.16倍
だったので
水の上昇温度も0.16倍と考えられます。
その値は
$$7.5℃×0.16=1.2℃$$
です。
実験2では5分で水の温度が1.2℃上昇している、ということです。
実験開始から5分後の水の温度が19.4℃なので
実験開始から10分後では、さらに1.2℃上昇するので
$$19.4℃+1.2℃=20.6℃$$
まで水の温度が上昇していることになります。
空欄Ⅱの答えは20.6℃です。
大問5の解説
(2)
まず地点Aと地点Bの記録からP波の速さを求めます。
地点Aと地点Bと震源が同一直線上にあると仮定します。
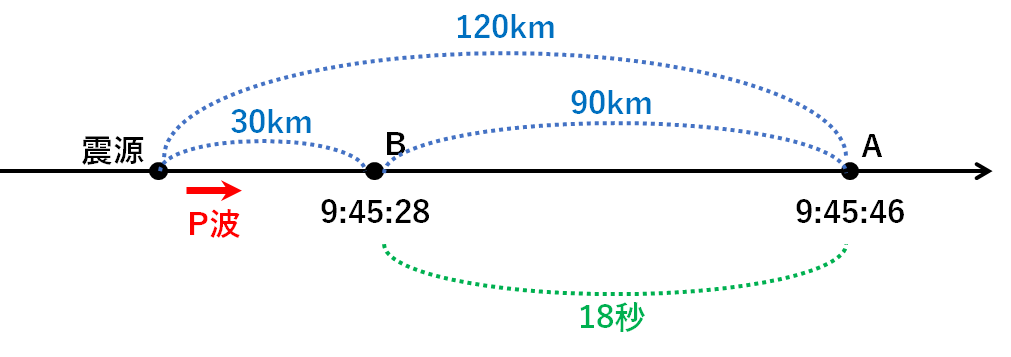
その距離やP波の到着時刻をまとめると↓のようになります。
地点Aと地点Bの間の距離は90km。
P波の到着時刻の差は18秒。
これを用いてP波の速さは
$$\frac{90km}{18秒}=5km/s$$
5km/sとなります。
次にいま求めたP波の速さを使って、地震の発生時刻を求めます。
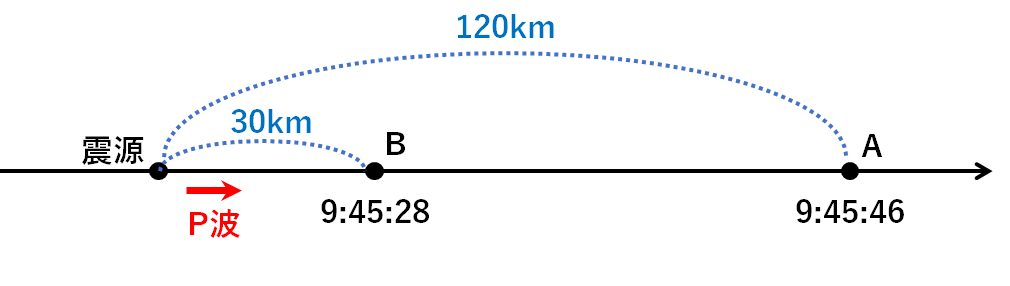
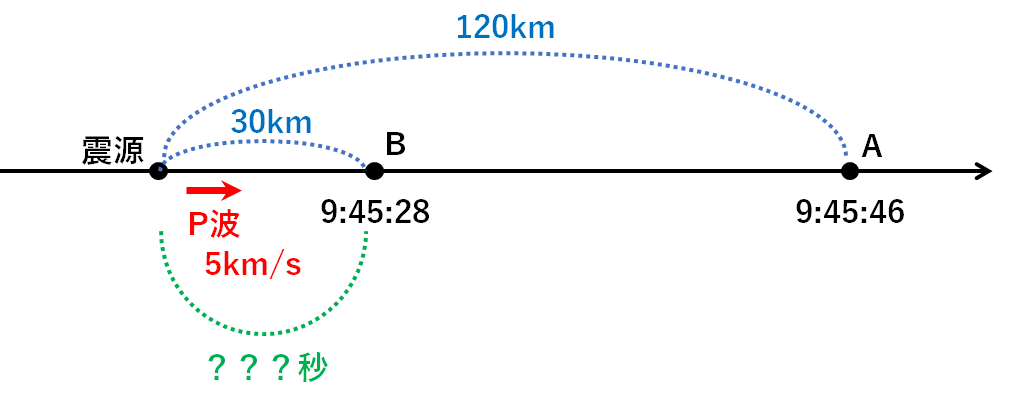
↓の図から
震源と地点Bの距離は30km。
P波の速さは5km/s。
これを用いてP波が地点Bに到着するのにかかった時間は
$$\frac{30km}{5km/s}=6秒$$
したがって地震発生時刻は
9時45分28秒の6秒前→9時45分22秒
となります。
そして地震発生時刻を使って、S波の速さを求めます。
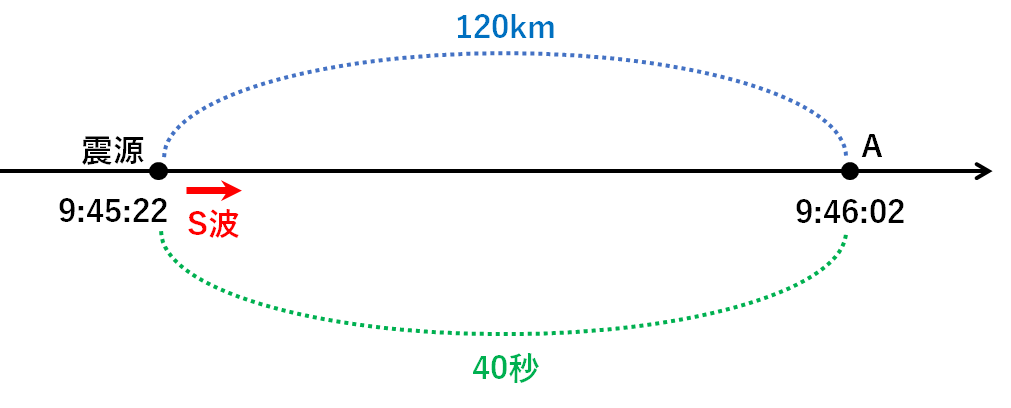
今度は地点AのS波の到着時刻に注目。(↓の図)
震源からA地点までの距離は120km。
S波がA地点に到着するまでにかかった時間は40秒。
これを用いてS波の速さは
$$\frac{120km}{40秒}=3km/s$$
3km/sとわかります。
以上からS波の速さは、P波の速さの何倍かを計算すると
$$3km/s÷5km/s=0.6倍$$
となります。
(3)
問題文より、緊急地震速報が発令されたのは
地点B(震源から30km)にP波が到着した4秒後
です。
すなわち9時45分32秒に緊急地震速報が発令されたのです。
ここで地点BでのS波の到着時刻を求めておきましょう。
(2)より
S波の速さは3km/s
地震発生時刻は9時45分22秒
でした。
地点Bは震源からの距離が30kmなので、S波の到着にかかる時間は
$$\frac{30km}{3km/s}=10秒$$
となります。
したがって地点BでのS波が到着した時刻は
9時45分22秒の10秒後→9時45分32秒
です。
緊急地震速報の発令は9時45分32秒なので
B地点では緊急地震速報の発令と同時に、S波が到着することになります。
B地点より震源に近い地点では、
緊急地震速報よりS波の到着の方がはやい
という事態になります。
一方,A地点(震源から120km)でのS波の到着時刻は9時46分02秒です。
これは緊急地震速報発令から30秒後です。
以上をグラフに表しましょう。(↓の図)
大問6の解説
(1)
図1のオリオン座の動きについて考えます。
問題文より
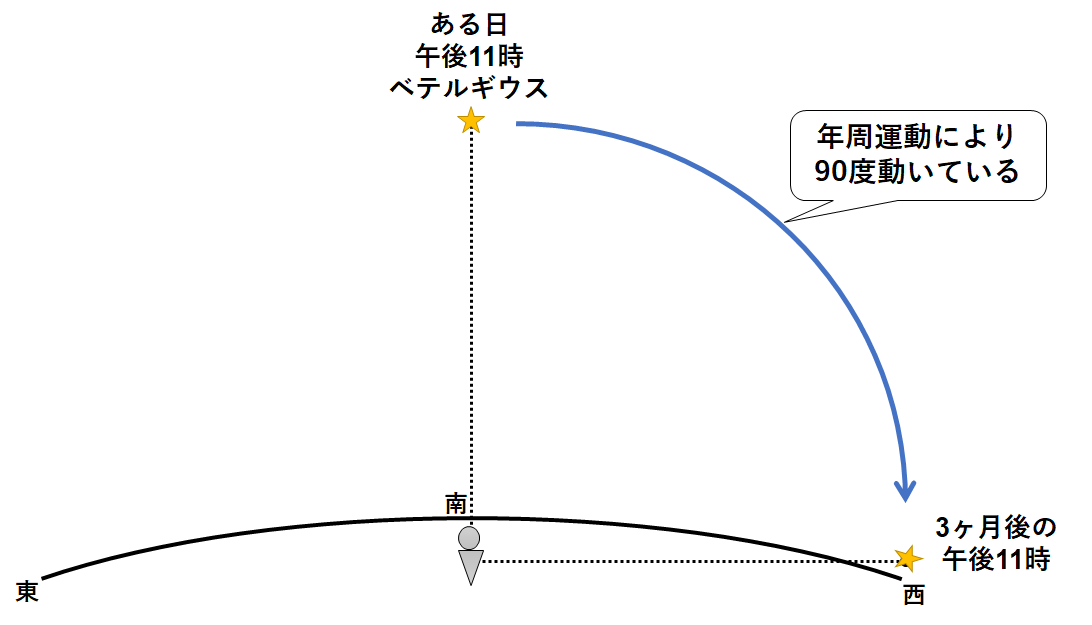
ある日の午後11時に、オリオン座のベテルギウスが南中しました。
この3ヶ月後の同時刻でのベテルギウスの位置は
年周運動を考えて、↓のように90度動いています。
この問いでは
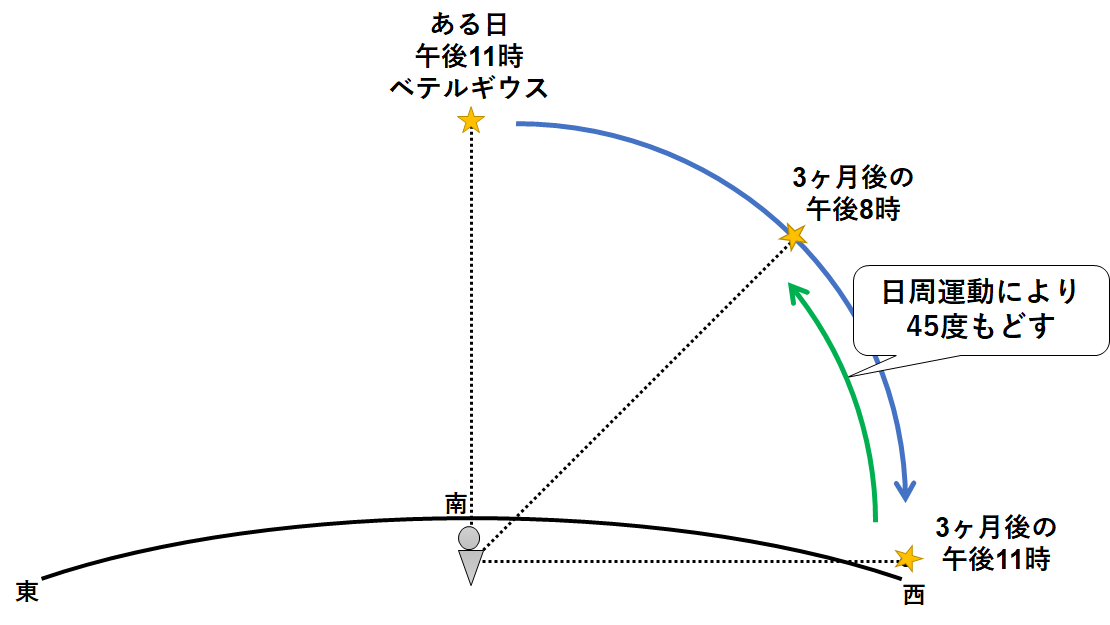
3ヶ月後の午後8時でのベテルギウスの位置を考えていますから
これは↑の図の3時間前。
日周運動を考えて、↓のように45度もどった位置にあります。
したがって初期の位置より45度、西にずれて見えます。
北の空の場合も同様で、北斗七星は45度だけずれたBの位置に見えます。



コメント(承認された場合のみ表示されます)