中2物理【オームの法則】

このページでは「オームの法則とは何か？」や「オームの法則」を使った回路計算の解き方を解説しています。

電流・電圧について理解が不十分だと思う人は→【電流と電圧】←のページを参考にしてみてください。

 

動画による解説は↓↓↓

 

1．オームの法則

 

1つの電熱線に流れる電流と電圧には比例の関係があります。

これをオームの法則と呼びます。

 

オームの法則を式にすると…

$$電圧(V)＝(比例定数)×電流(A)$$

この比例定数には名前があって、抵抗と言います。

 

抵抗という値は電流の流れにくさを意味します。

単位は【Ω】（オーム）。

※ドイツのオームさんの名前が由来です。

 

上の式を書き直します。

$$電圧(V)＝抵抗(Ω)×電流(A)$$

となります。

 

他にもこの式を変形すると

$$抵抗(Ω)＝\frac{電圧(V)}{電流(A)}$$

$$電流(A)＝\frac{電圧(V)}{抵抗(Ω)}$$

とできます。

 

これらの公式はとても大事！必ず使いこなせるようにしよう！

2．オームの法則の計算問題

実際にオームの法則を使って問題を解いてみましょう。

 

頭に入れておくべきポイントは3つ。

 

以下に例題をのせます。考えてみてくださいね。

 

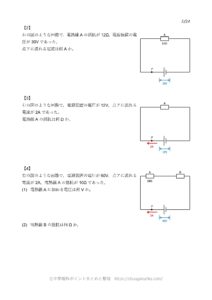
【例題1】

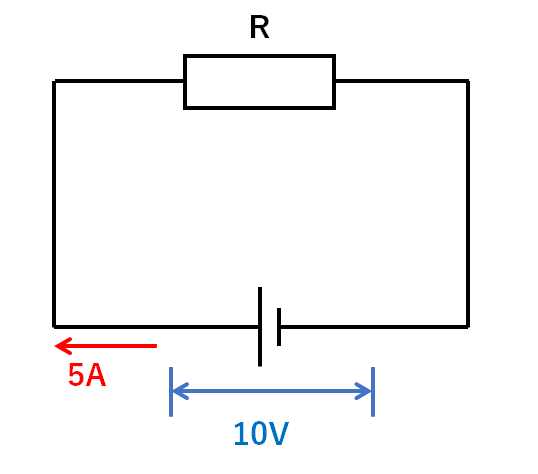
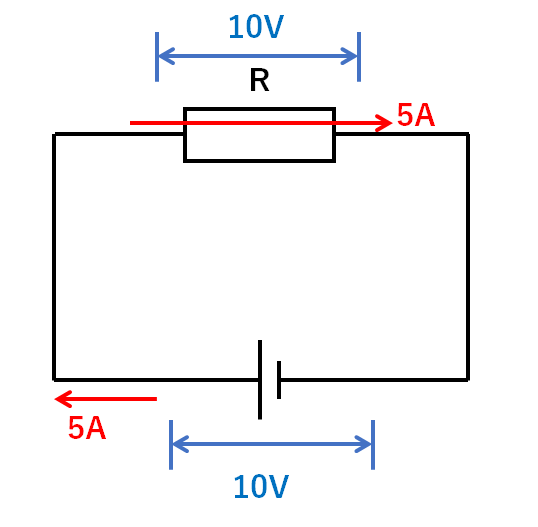
電熱線Rの抵抗を求めなさい。

---

(答)

電熱線Rに流れる電流は5A、電圧は10Vです。(↓の図)

 

よってオームの法則より…

 

$$抵抗(Ω)＝\frac{電圧(V)}{電流(A)}＝\frac{10V}{5A}＝2Ω$$

となります。

 

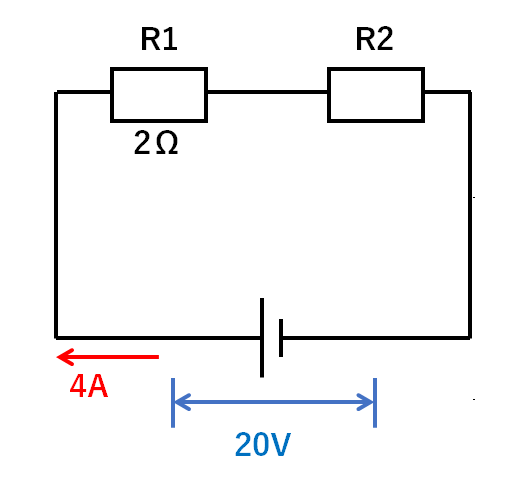
【例題2】

電熱線R₂の抵抗を求めなさい。

---

(答)

電流の様子を書き足すと↓にようになります。

「電圧・電流・抵抗」のうち2つがわかっている電熱線を探します。

 

それはR₁です。

 

R₁に流れる電流は4A、抵抗は2Ωなので

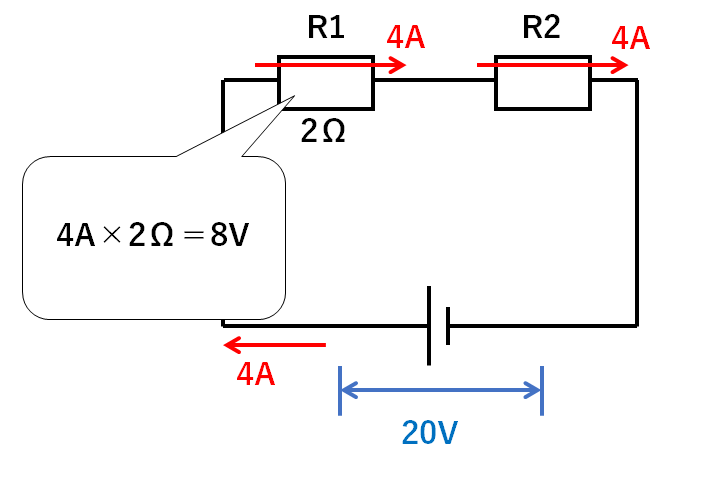
$$電圧(V)＝抵抗(Ω)×電流(A)＝2Ω×4A＝8V$$

の電圧がR₁には加わっています。

 

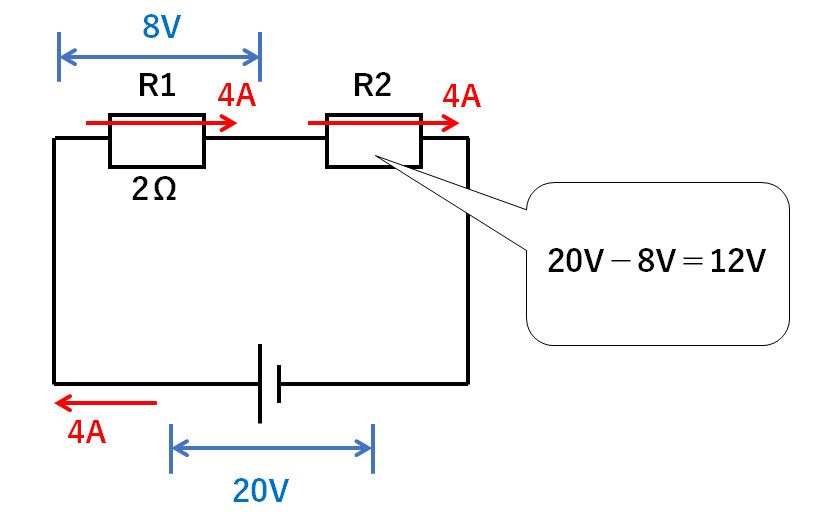
電源の電圧は20Vなので、R₂には

$$20V－8V＝12V$$

の電圧が加わっています。(↓の図)

 

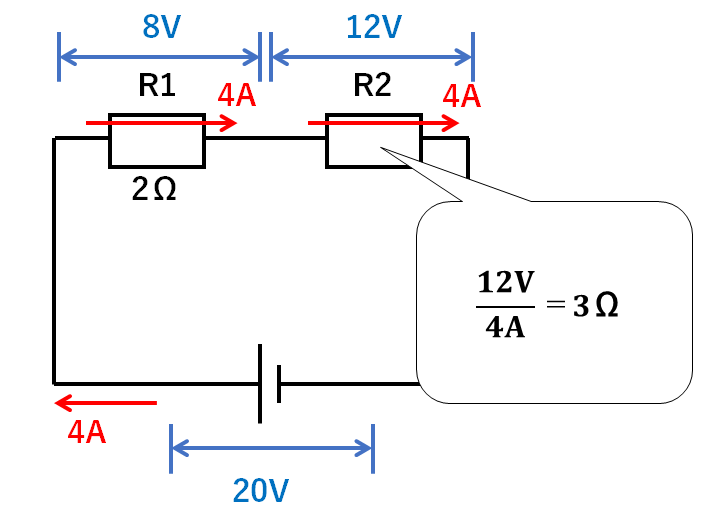
またR₂の電流は4Aだから

$$抵抗(Ω)＝\frac{電圧(V)}{電流(A)}＝\frac{12V}{4A}＝3Ω$$

となります。

 

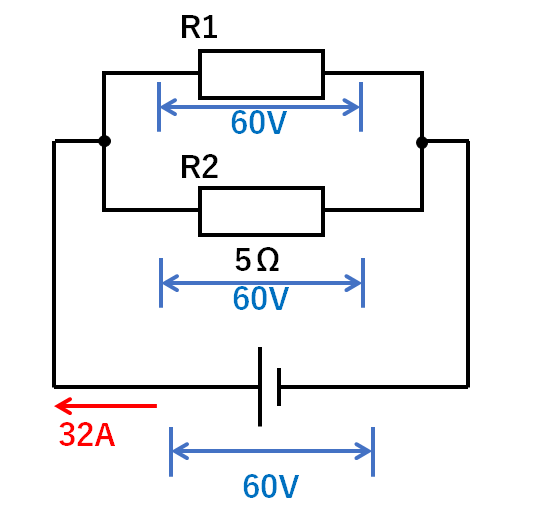
【例題3】

電熱線R₁の抵抗を求めなさい。

---

(答)

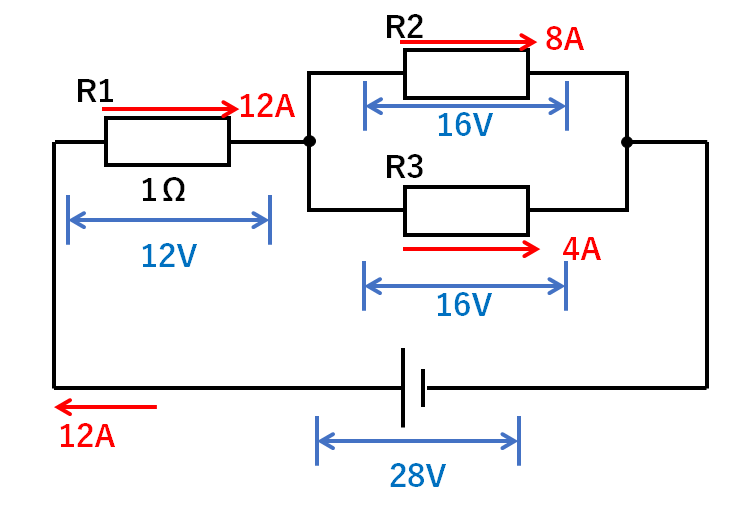
電圧の加わり方は↓のようになります。

電源の電圧を1つの道筋で使い切って帰りますよね。

※よくわからない人は→【電流と電圧】←を参考に。

 

次に「電圧・電流・抵抗」のうち2つがわかっている電熱線を探します。

 

それはR₂です。

R₂の抵抗は5Ω、加わる電圧は60Vなので

$$電流(A)＝\frac{電圧(V)}{抵抗(Ω)}＝\frac{60V}{5Ω}＝12A$$

の電流がR₂には流れています。

 

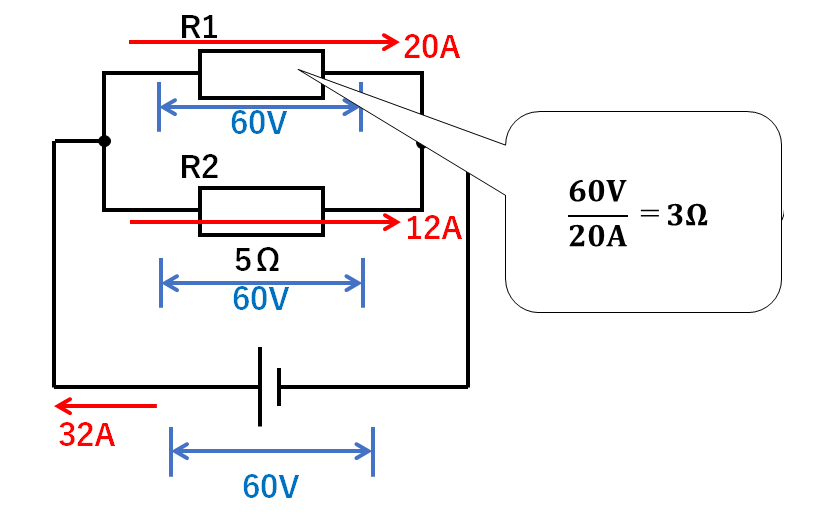
全体の電流が32Aなので

 

 

$$32A－12A＝20A$$

の電流がR₁には流れていますね。

 

さらに電圧は60Vなので

$$抵抗(Ω)＝\frac{電圧(V)}{電流(A)}＝\frac{60V}{20A}＝3Ω$$

となります。

 

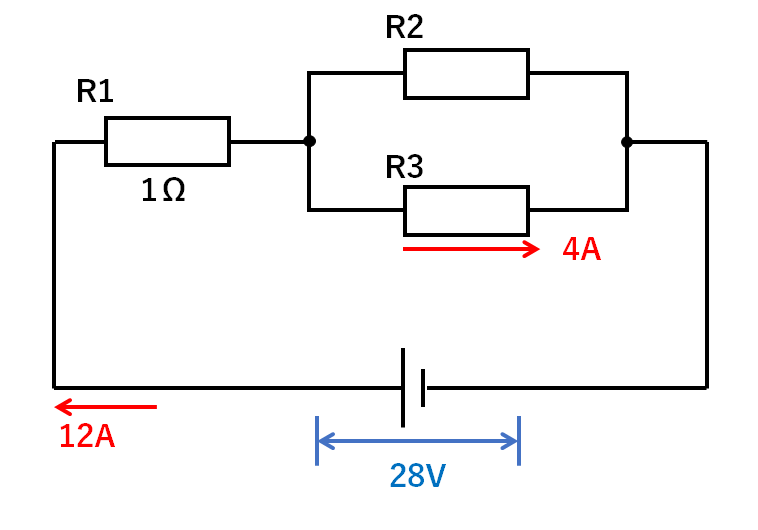
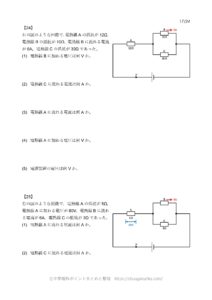
【例題4】

電熱線R₂とR₃の抵抗を求めなさい。

---

(答)

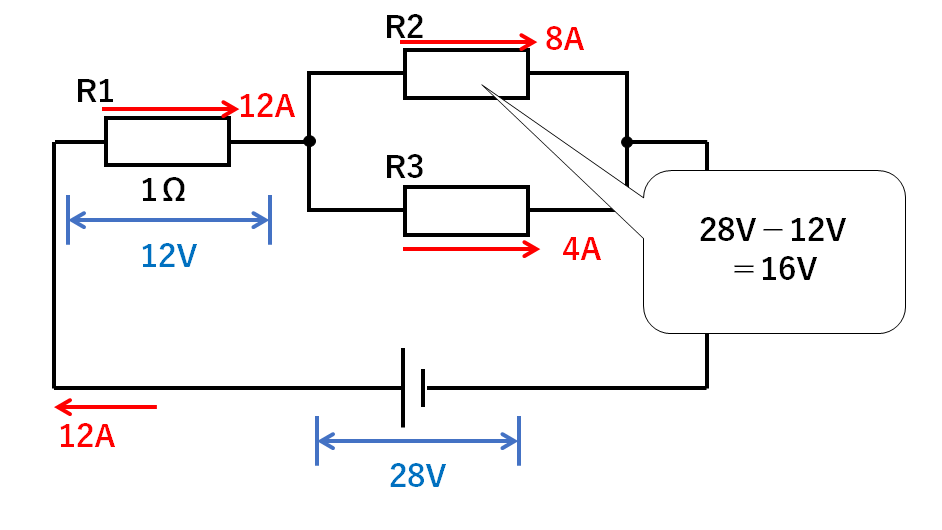
流れている電流は次のようになります。

 

次に「電圧・電流・抵抗」のうち2つがわかっている電熱線を探します。

 

それはR₁です。

R₁の抵抗は1Ω、電流は12Aなので

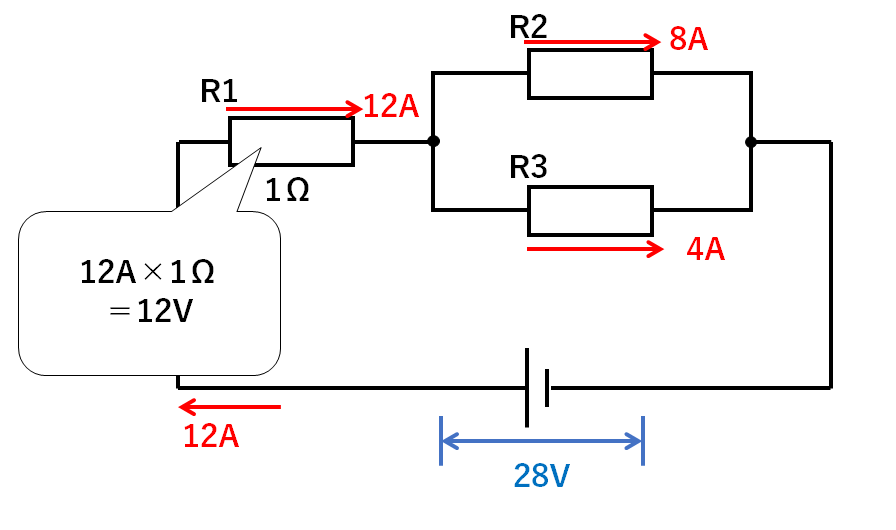
$$電圧(V)＝抵抗(Ω)×電流(A)＝1Ω×12A＝12V$$

の電圧がR₁には加わっています。

 

電源の電圧は28Vなので、28Vのうち12VをR₁で使って

$$28V－12V＝16V$$

の電圧が残っています。

 

これがR₂に加わります。(↓の図)

R₃にも加わります。(電圧は1つの道筋で使い切るので)

 

 

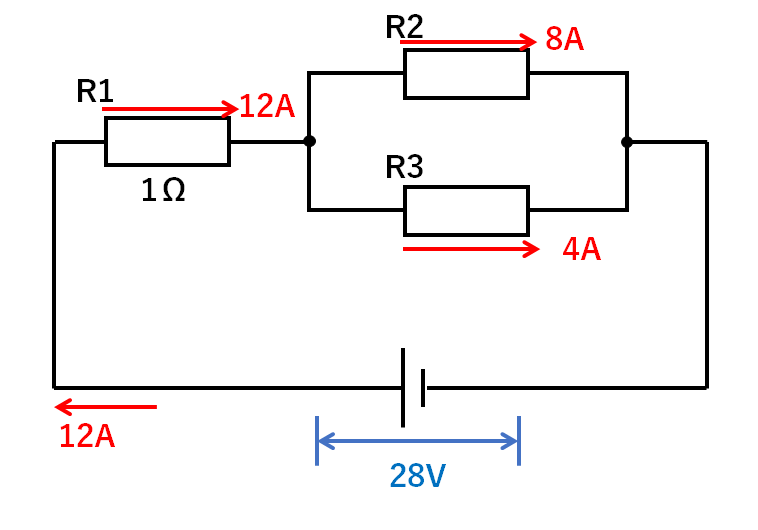
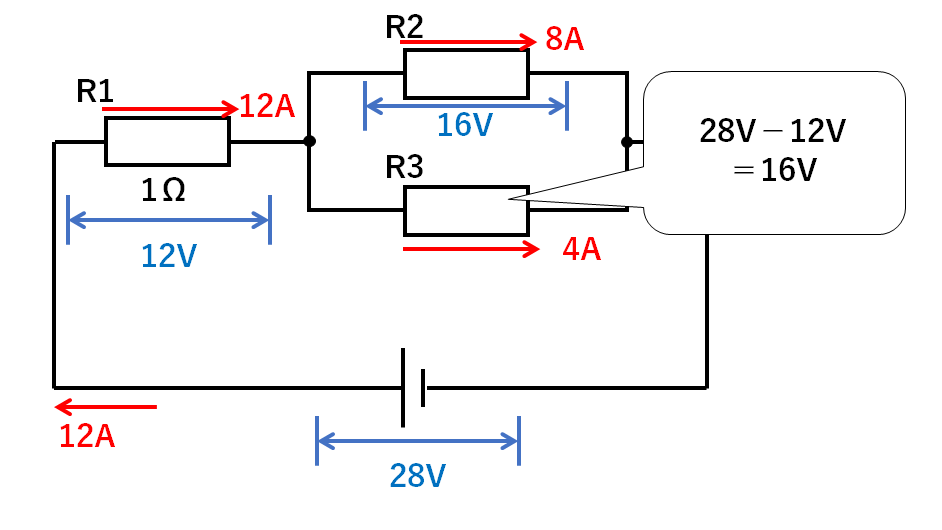
R₂の電圧が16V、電流が8Aなので

$$R2の抵抗(Ω)＝\frac{電圧(V)}{電流(A)}＝\frac{16V}{8A}＝2Ω$$

 

R₃の電圧が16V、電流が4Aなので

$$R3の抵抗(Ω)＝\frac{電圧(V)}{電流(A)}＝\frac{16V}{4A}＝4Ω$$

となります。(↓の図)

 

 

 

 

こちらもどうぞ

オームの法則に関する計算ドリルを販売中です。

このページの例題にあるような問題をたくさん掲載しています。

1つ220円(税込)です。

PDF形式のダウンロード販売です。

　　　　

よければどうぞ。