*このページは教科書を超える発展的な内容を含みます。
電流回路の中でも、主に高校で学習する「ブリッジ回路」や「ホイートストンブリッジ」について、できるだけ中学生にも簡単に解ける方法を解説しています。
動画による解説は↓↓↓
チャンネル登録はこちらから↓↓↓
1.ブリッジ回路
↓のような回路をブリッジ回路といいます。
通常のオームの法則の電流回路の問題だと思うと解けないのが厄介なところです。
高校入試で出題されるのは主に2パターンです。
パターン❶
パターン❷
重要なのは中央の部分に流れる電流の向きと大きさです。
抵抗によっては上向きの電流、または下向きの電流もあり得ます。
また電流が流れないということもあり得ます。
この問題を解くには
をマスターしておくべきです。
このページではパターン❶の問題を解説します。
2.ブリッジ回路の解法
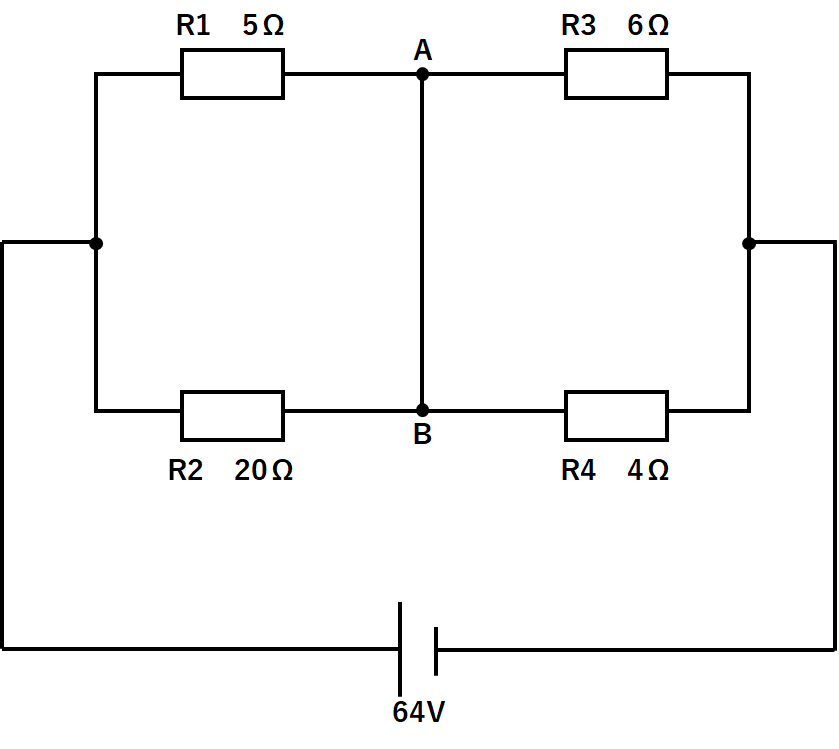
例題1
例題1の答えと解説
ブリッジ回路の問題は、原則以下のように書き換えて問題を考えてみます。
このときR1~R4に流れる電流の大きさを考えます。
①回路全体の抵抗を求める
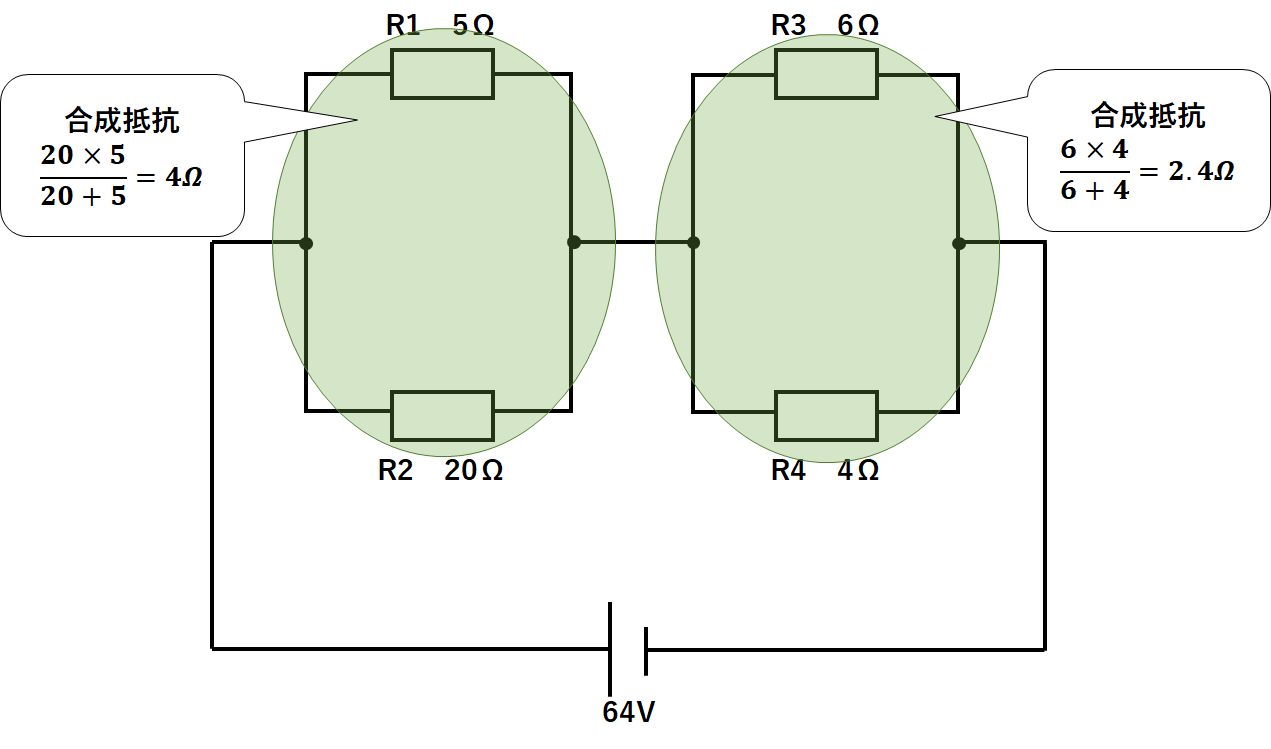
まず左側(R1とR2)の部分と右側(R3とR4)の部分の合成抵抗をそれぞれ求めましょう。
並列につながっている部分の合成抵抗の求め方は
$$\frac{積}{和}$$
です。
よって左側(R1とR2)の部分は
$$左側の合成抵抗=\frac{5Ω×20Ω}{5Ω+20Ω}=4Ω$$
右側(R3とR4)の部分は
$$右側の合成抵抗=\frac{6Ω×4Ω}{6Ω+4Ω}=2.4Ω$$
となります。(↓の図)
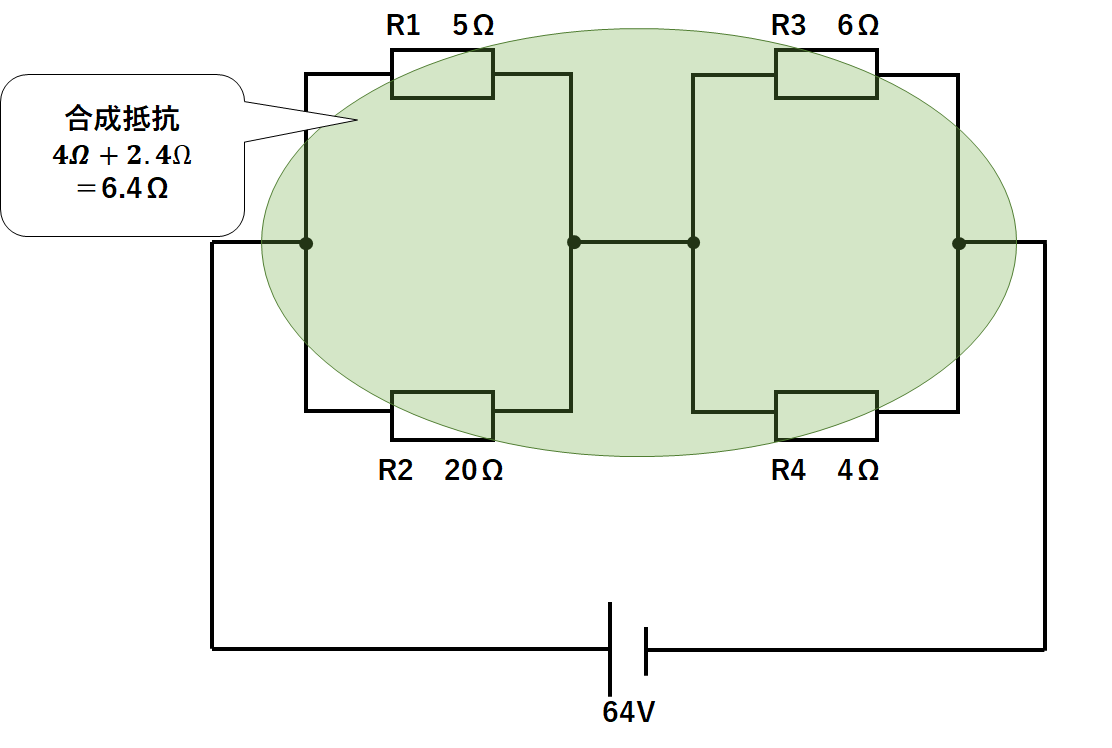
よって回路全体の抵抗は
$$4Ω+2.4Ω=6.4Ω$$
となります。(↓の図)
②回路全体に流れる電流を求める
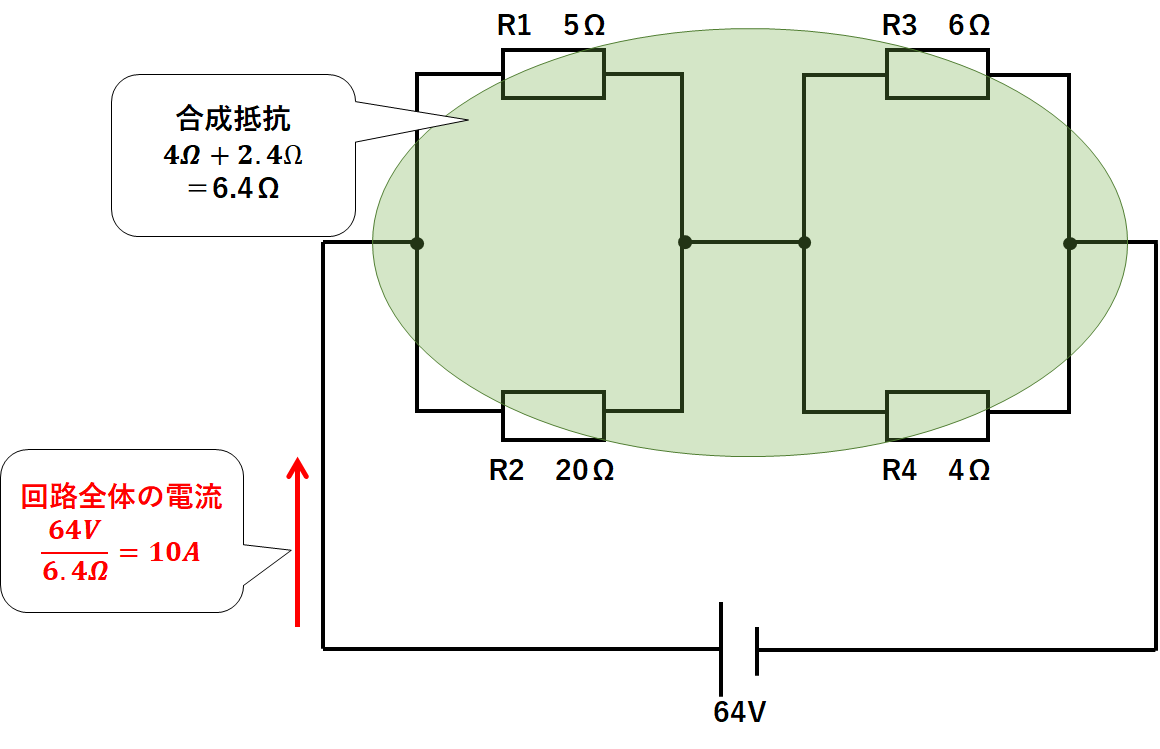
次に回路全体に流れる電流を求めましょう。
電源の電圧が64V、回路全体の抵抗が6.4Ωなので
オームの法則より
$$回路全体の電流=\frac{64V}{6.4Ω}=10A$$
となります。(↓の図)
③抵抗1つ1つに流れる電流を求める
ではR1~R4に流れる電流はそれぞれ何Aか求めましょう。
このとき
並列回路では抵抗の逆比=電流の比となる
ことを利用するとすばやく求めることができます。
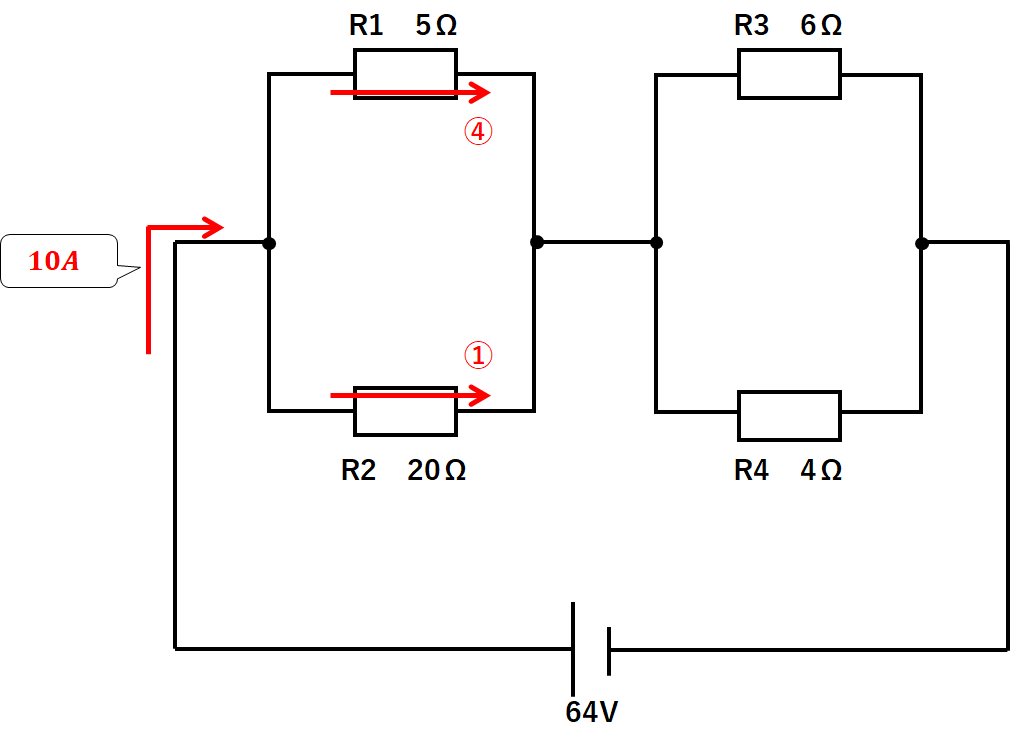
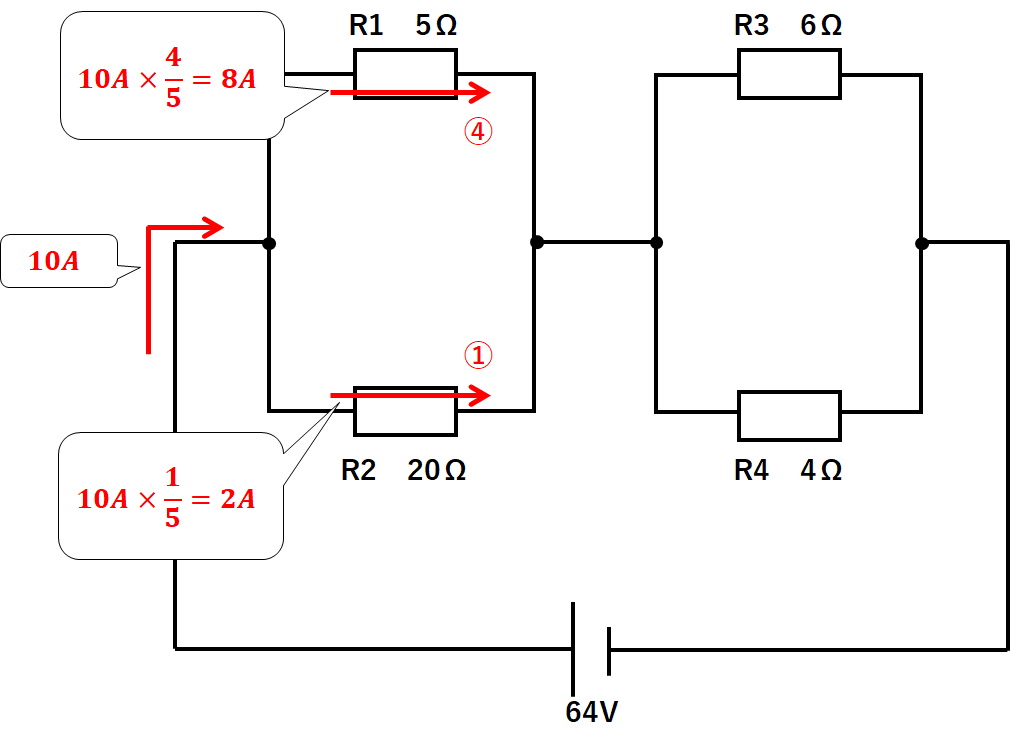
左側(R1とR2)を見てみます。
$$R1の抵抗:R2の抵抗=5Ω:20Ω=1:4$$
なので
$$R1の電流:R2の電流=4:1$$
となります。
10Aが4:1に分かれて流れていくことになるので
$$R1の電流=10A×\frac{4}{5}=8A$$
$$R2の電流=10A×\frac{1}{5}=2A$$
となります。(↓の図)
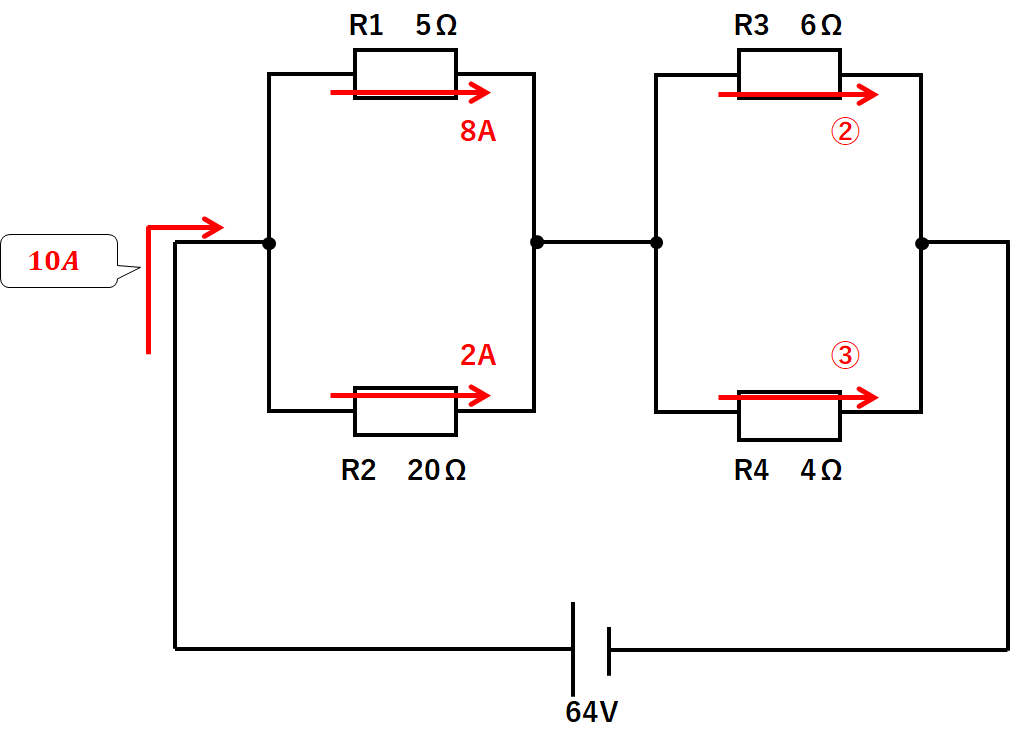
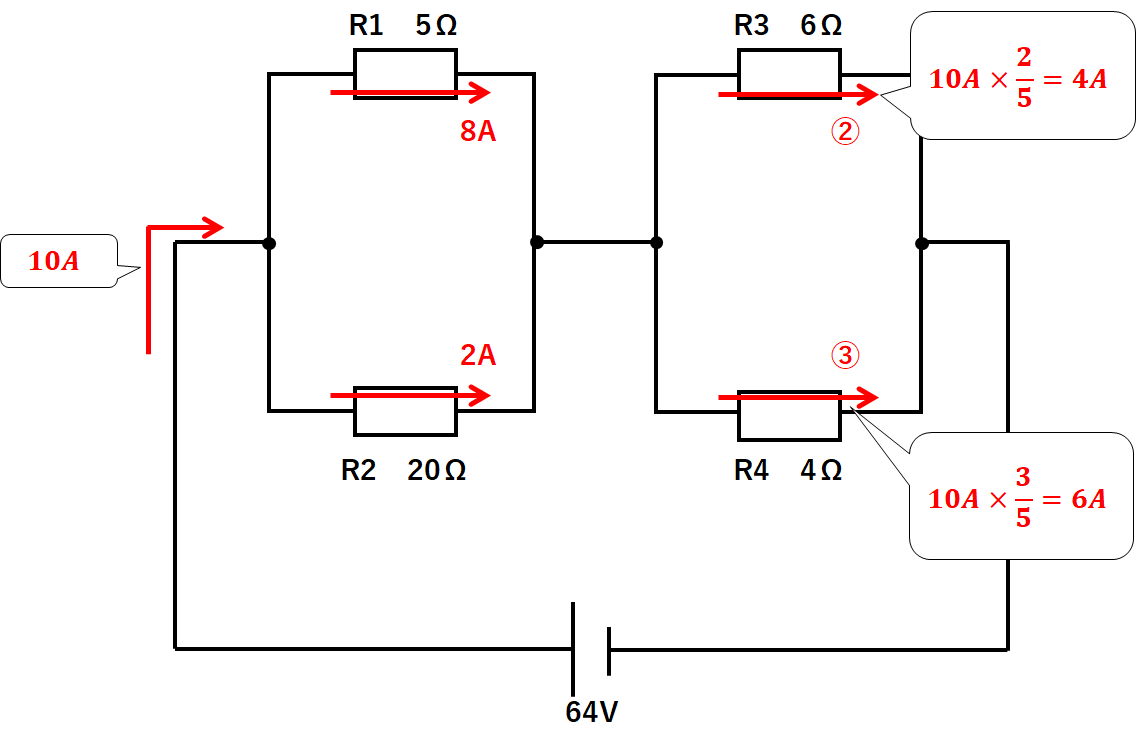
右側(R3とR4)も同じように電流を求めましょう。
$$R3の抵抗:R4の抵抗=6Ω:4Ω=3:2$$
なので
$$R3の電流:R4の電流=2:3$$
となります。
10Aが2:3に分かれて流れていくことになるので
$$R3の電流=10A×\frac{2}{5}=4A$$
$$R4の電流=10A×\frac{3}{5}=6A$$
となります。(↓の図)
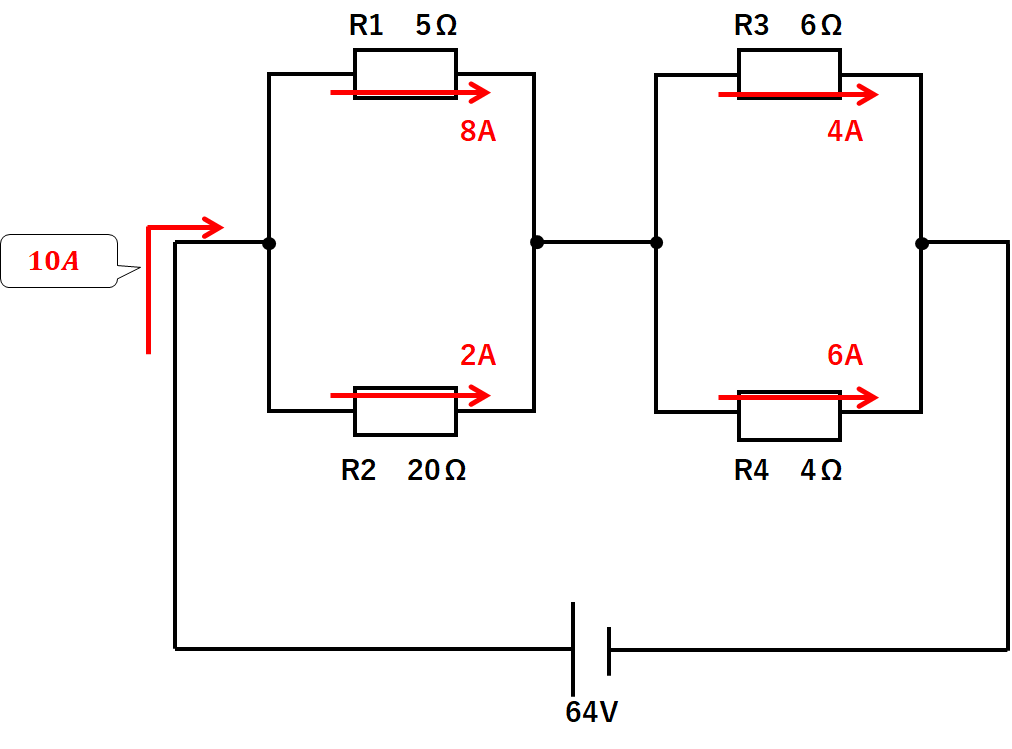
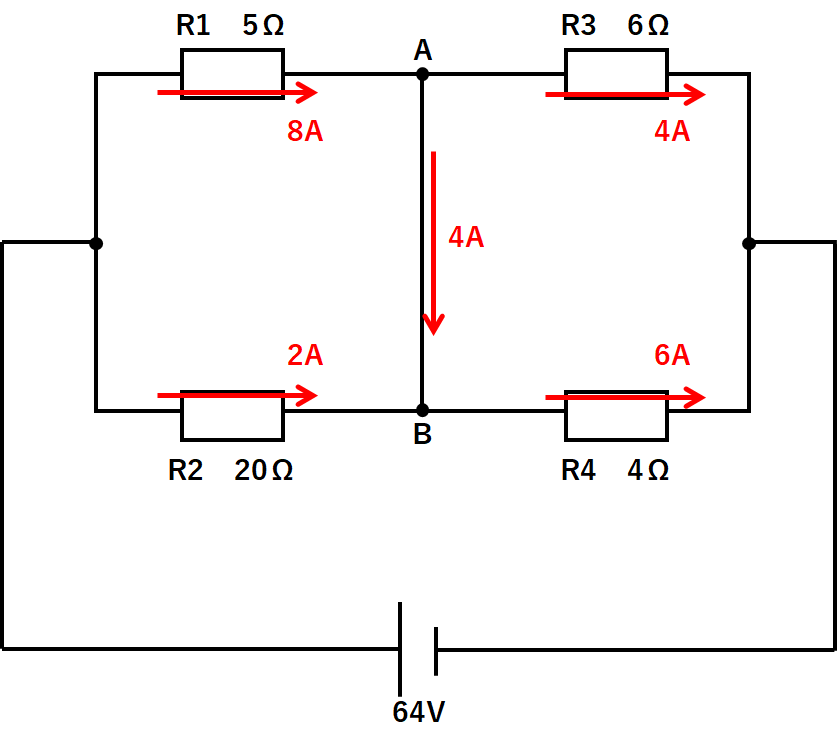
よって各抵抗に流れる電流は↓のようになっているとわかりました。
④元の回路に電流を書き戻す
先ほど求めた電流をもとの回路に書き加えます。(↓の図)
ここでABの部分を考えてみます。
R1に流れた電流8Aのうち、R3には4A流れたのです。
残り4AがAからBへと進んでいったと考えられます。
R2に流れた電流は2A、先ほどの電流4Aが合流して、R4に6A流れているわけです。
AからBへ4Aの電流が流れていることになります。
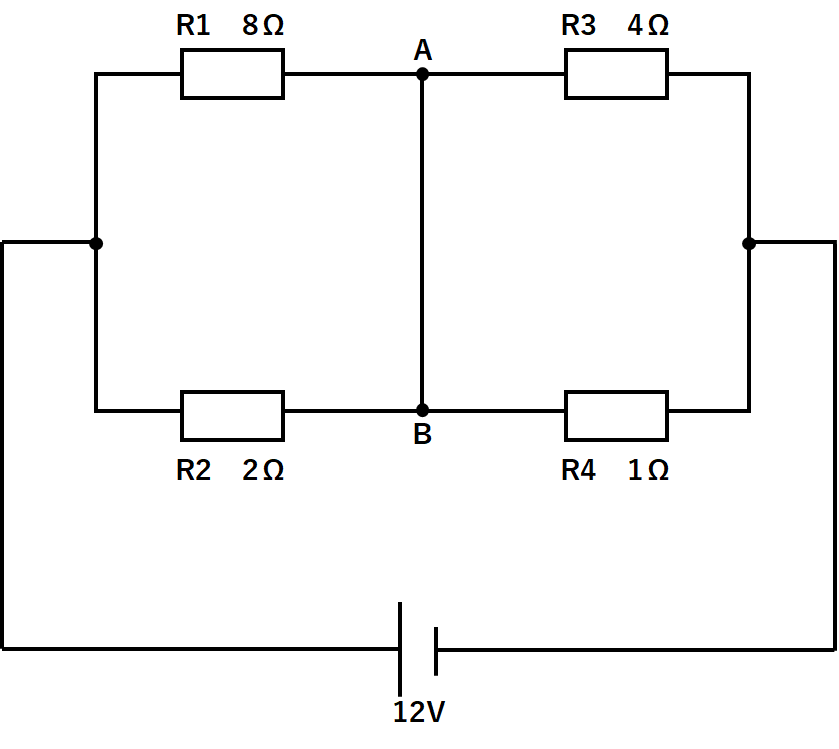
例題2
例題2の答えと解説
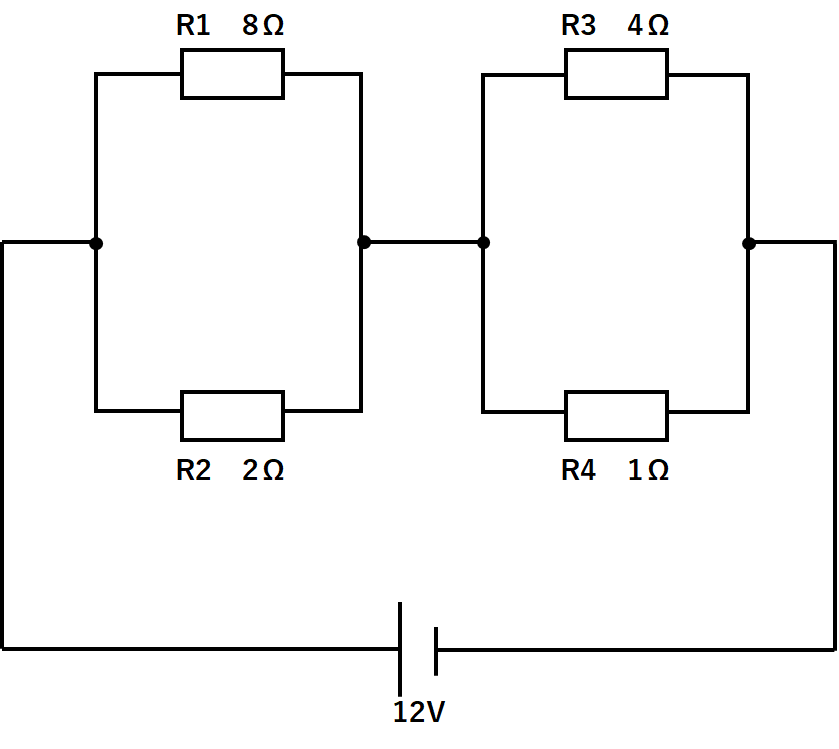
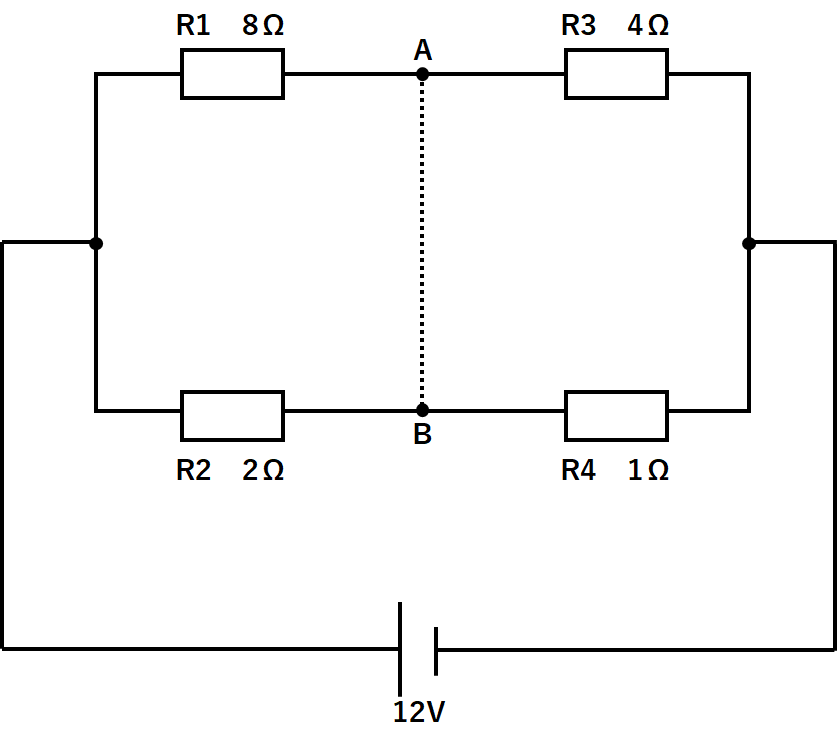
さきほどと同様に以下のように書き換えて問題を考えてみます。
このときR1~R4に流れる電流の大きさを考えます。
①回路全体の抵抗を求める
まず左側(R1とR2)の部分と右側(R3とR4)の部分の合成抵抗をそれぞれ求めましょう。
並列につながっている部分の合成抵抗の求め方は
$$\frac{積}{和}$$
でした。
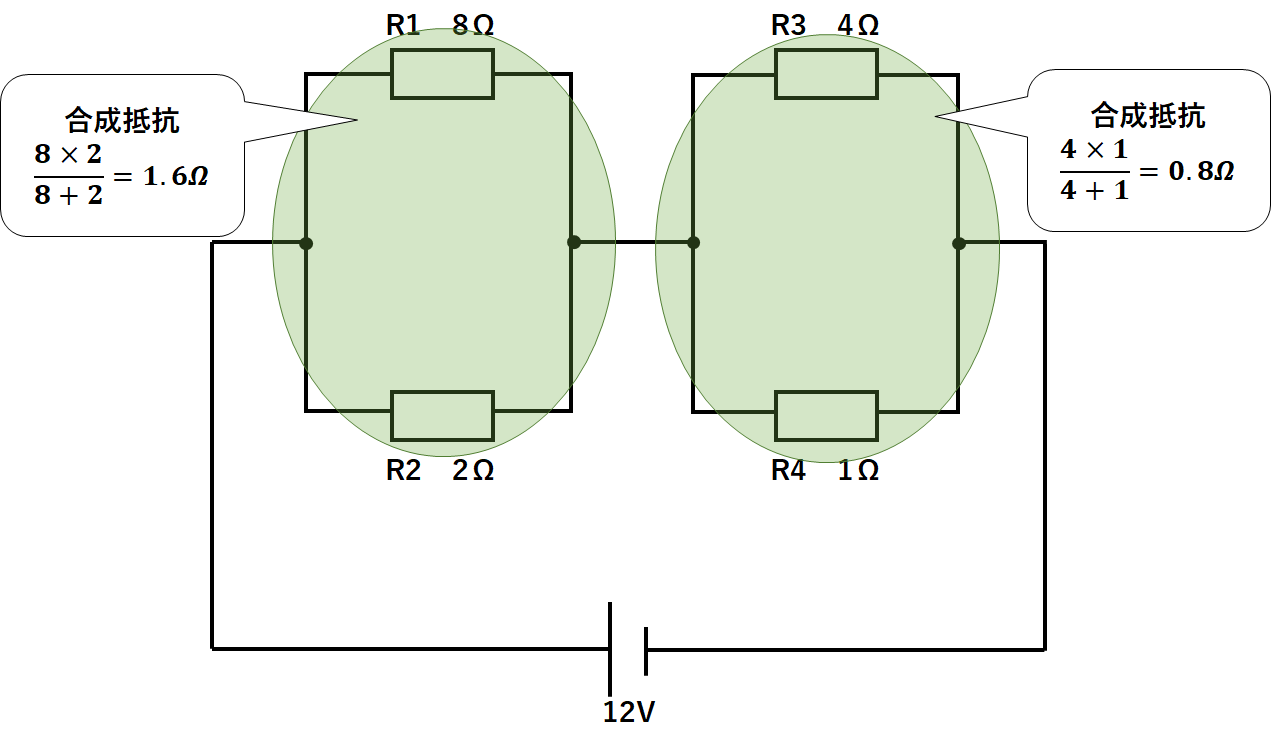
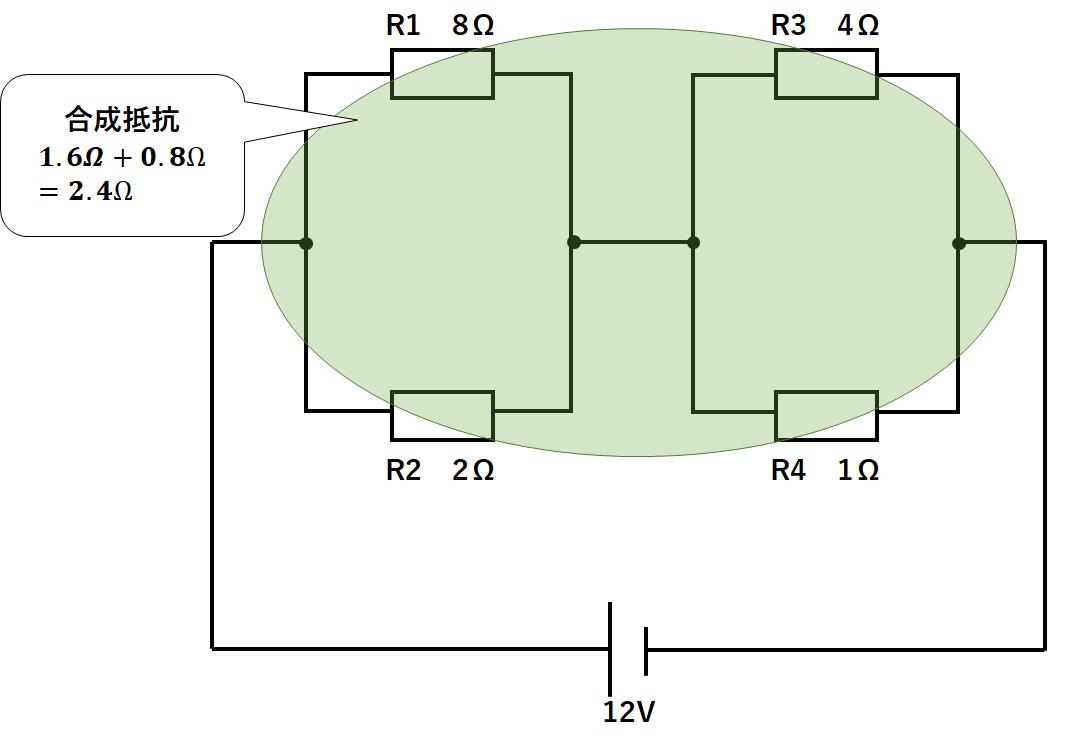
よって左側(R1とR2)の部分は
$$左側の合成抵抗=\frac{8Ω×2Ω}{8Ω+2Ω}=1.6Ω$$
右側(R3とR4)の部分は
$$右側の合成抵抗=\frac{4Ω×1Ω}{4Ω+1Ω}=0.8Ω$$
となります。(↓の図)
よって回路全体の抵抗は
$$1.6Ω+0.8Ω=2.4Ω$$
となります。
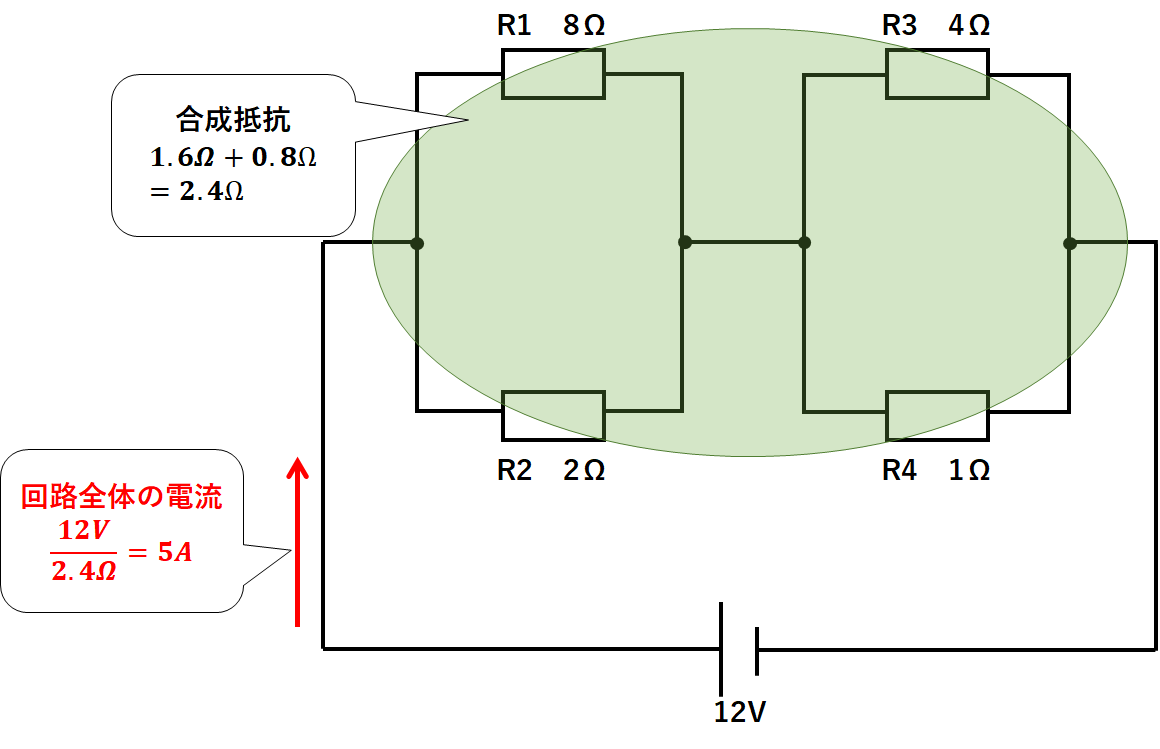
②回路全体に流れる電流を求める
次に回路全体に流れる電流を求めましょう。
電源の電圧が12V、回路全体の抵抗が2.4Ωなので
オームの法則より
$$回路全体の電流=\frac{12V}{2.4Ω}=5A$$
となります。
③抵抗1つ1つに流れる電流を求める
ではR1~R4に流れる電流はそれぞれ何Aか求めましょう。
このとき
並列回路では抵抗の逆比=電流の比
となっていることを利用するとすばやく求めることができます。
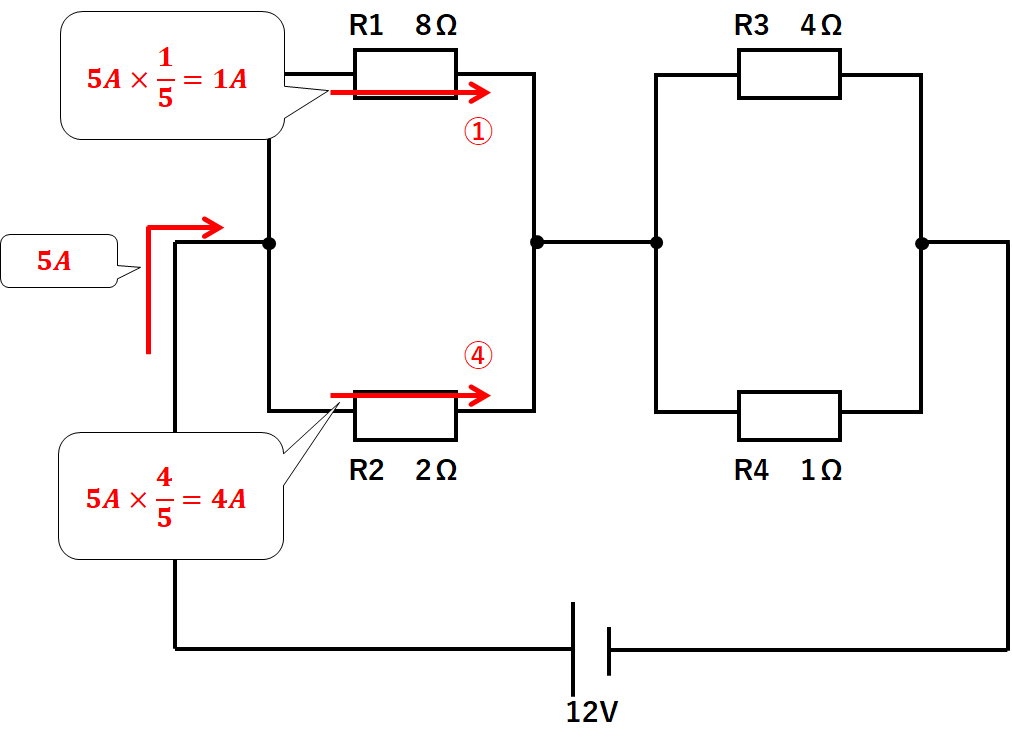
左側(R1とR2)を見てみます。
$$R1の抵抗:R2の抵抗=8Ω:2Ω=4:1$$
なので
$$R1の電流:R2の電流=1:4$$
となります。
5Aが1:4に分かれて流れていくことになるので
$$R1の電流=5A×\frac{1}{5}=1A$$
$$R2の電流=5A×\frac{4}{5}=4A$$
となります。(↓の図)
右側(R3とR4)も同じように電流を求めましょう。
$$R3の抵抗:R4の抵抗=4Ω:1Ω=4:1$$
なので
$$R3の電流:R4の電流=1:4$$
となります。
5Aが4:1に分かれて流れていくことになるので
$$R3の電流=5A×\frac{1}{5}=1A$$
$$R4の電流=5A×\frac{4}{5}=4A$$
となります。(↓の図)
よって各抵抗に流れる電流は↓のようになっているとわかりました。
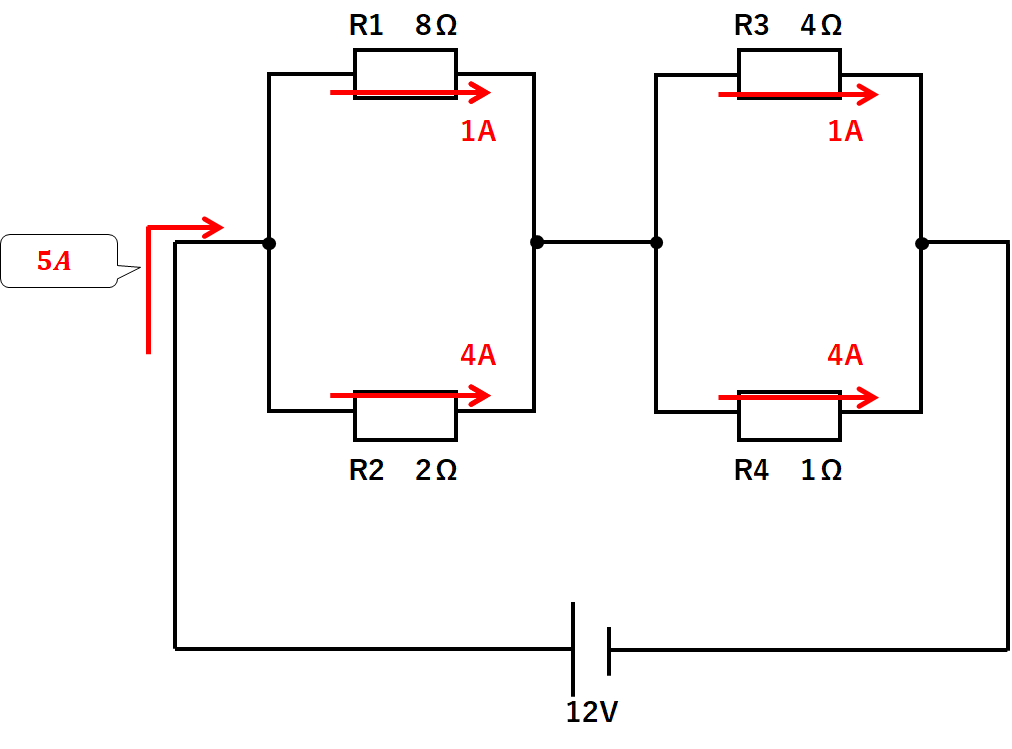
④元の回路に電流を書き戻す
先ほど求めた電流をもとの回路に書き加えます。(↓の図)
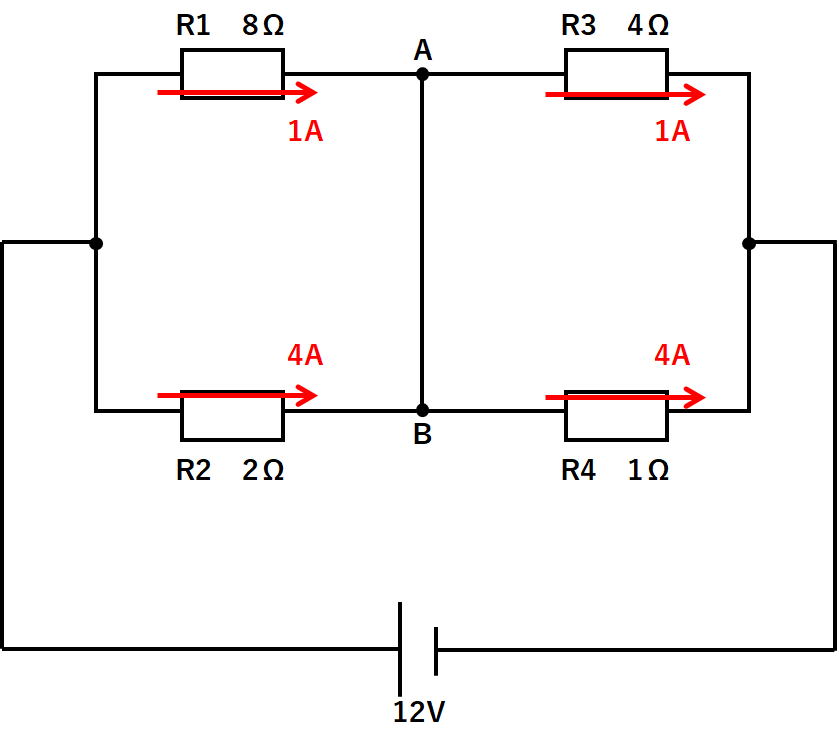
ここでABの部分を考えてみます。
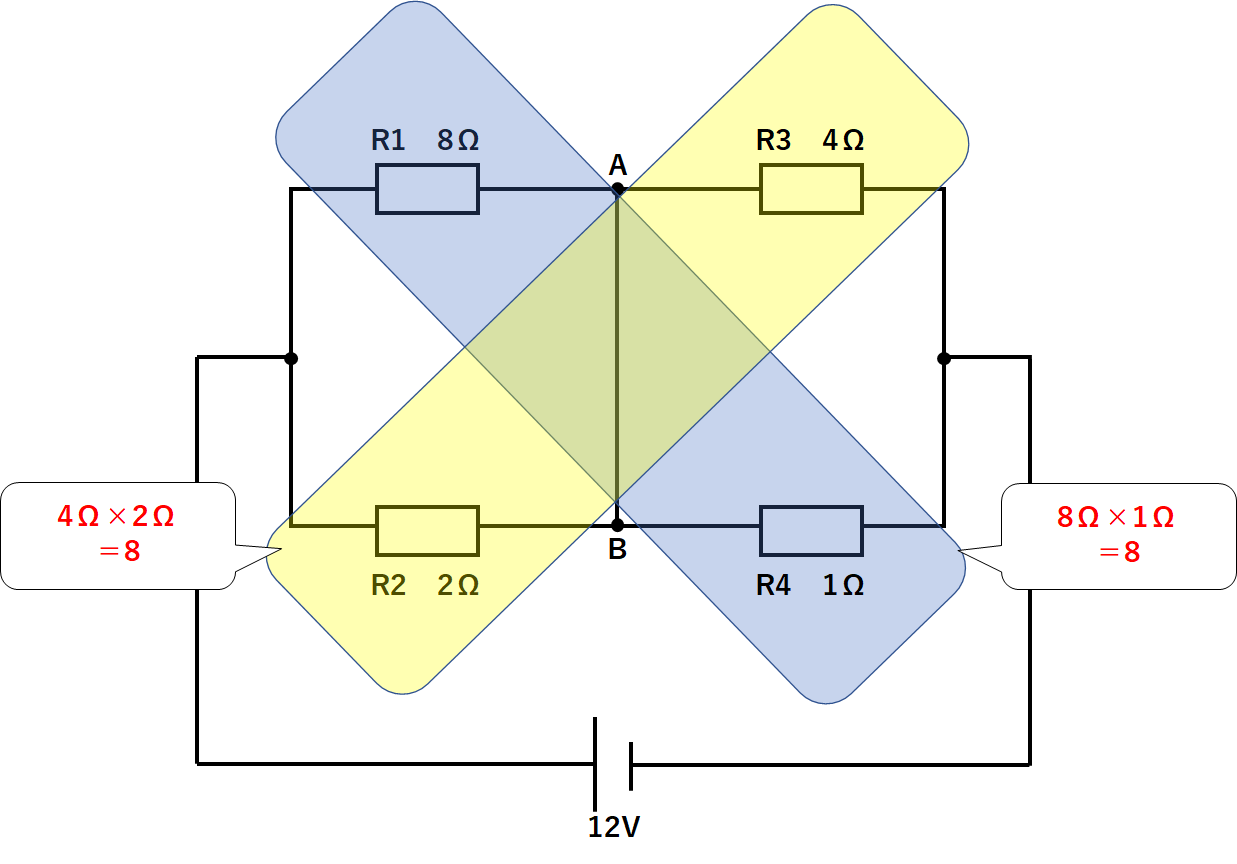
R1が4A、R3も4Aです。
R1に流れた電流4AがそのままR3に流れたのです。
同じようにR2が1A、R4も1Aです。
R2に流れた電流1AがそのままR4に流れたのです。
つまりABの部分にはまったく電流は流れていないのです。
よってABの部分の電流は0Aです。
POINT!
ブリッジ回路の問題は
①回路を書き換える
②回路全体の抵抗を求める
③回路全体に流れる電流を求める
④抵抗1つ1つに流れる電流を求める
⑤元の回路に電流を書き戻す
の手順で解きましょう。
ここで回路の抵抗に注目すると次にようになっていることがわかります。
となっていることがわかります。
(このような回路をホイートストンブリッジといいます)
このときAB部分には電流が流れないのです。
もし問題を解く前に
$$R1×R4=R2×R3$$
となっていることに気づけば、AB部分の電流は0Aとすぐ判断できます。
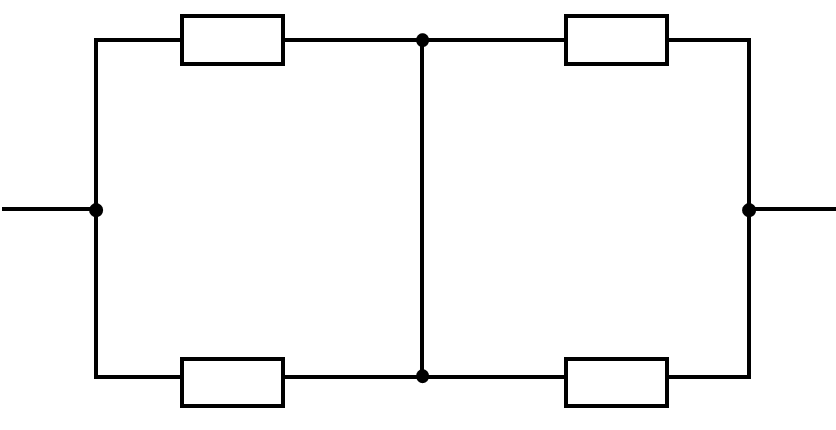
また次のようにAB部分の導線を省略して考えて見ることが可能です。
POINT!
R1×R4=R2×R3となっているとき
AB部分には電流が流れない。
※より発展的な内容を→【ブリッジ回路その2】←に書いています。余力のある人はどうぞ。




コメント(承認された場合のみ表示されます)
[…] 中2物理【*ブリッジ回路】 – 中学理科 ポイントまとめと整理 […]