このページでは「抵抗の比」や「抵抗の逆比」を使って電流や電圧の比を計算する方法を紹介しています。
このページを理解するには
を理解しておく必要があります。
1.直列回路の抵抗の比
■直列回路では
抵抗(電熱線)に流れる電流は同じであるため
抵抗の比=電圧の比
となる。
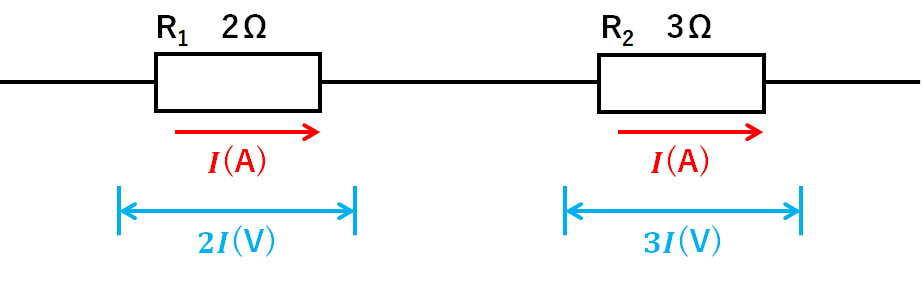
次のような直列回路を見てみましょう。(ただし、電源装置は省略)
この回路にI(A)の電流が流れ込んだとします。(↓の図)
↓の図のように
$$R1の電流=I(A)$$
$$R2の電流=I(A)$$
となります。
ここでオームの法則を思い出しましょう。
$$電圧(V)=抵抗(Ω)×電流(A)$$
オームの法則を用いることで
$$R1の電圧=2Ω×I(A)=2I(V)$$
$$R2の電流=3Ω×I(A)=3I(V)$$
であることがわかります。(↓の図)
ここで条件を振り返ってみましょう。
▼抵抗の比
$$R1の抵抗:R2の抵抗=2:3$$
▼電圧の比
$$R1の電圧:R2の電圧=2I:3I=2:3$$
となります。
つまり直列回路では
抵抗の比=電圧の比
となるのです。
2.並列回路の抵抗の比
■並列回路では
抵抗(電熱線)に加わる電圧は同じであるため
抵抗の逆比=電流の比
となる。
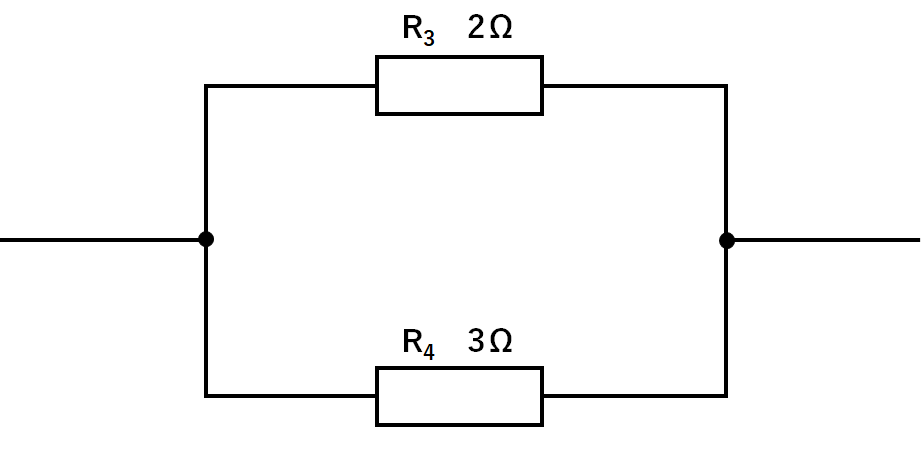
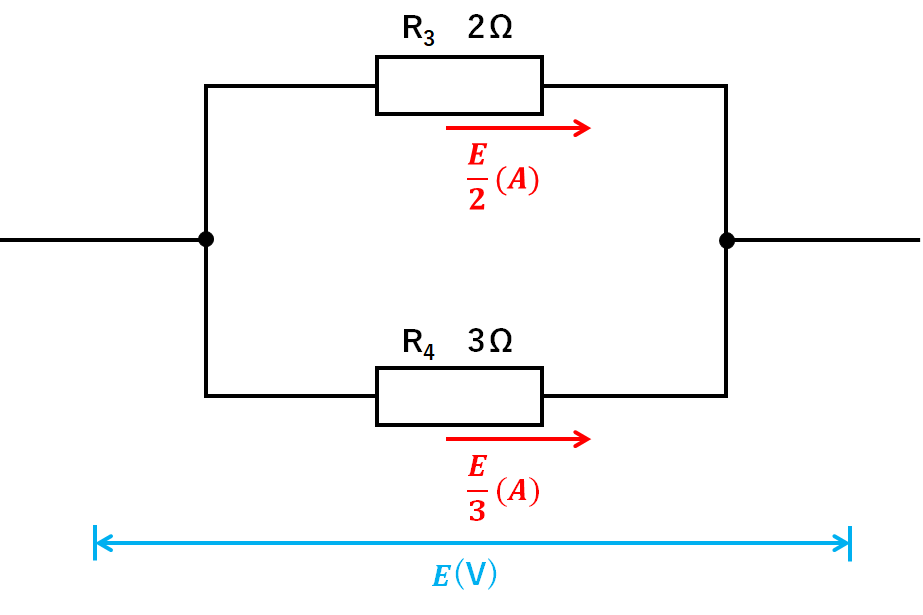
次のような並列回路を見てみましょう。(ただし、電源装置は省略)
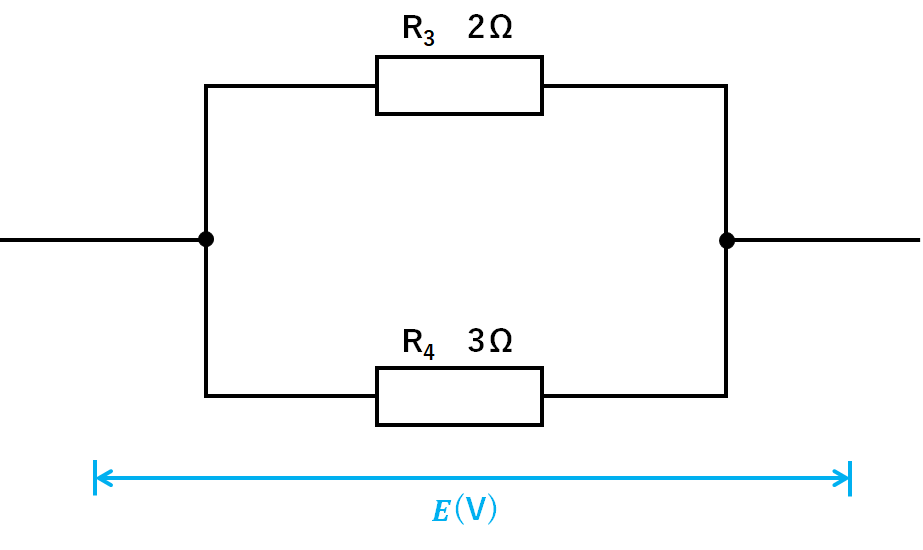
この回路にE(V)の電圧が加えたとします。(↓の図)
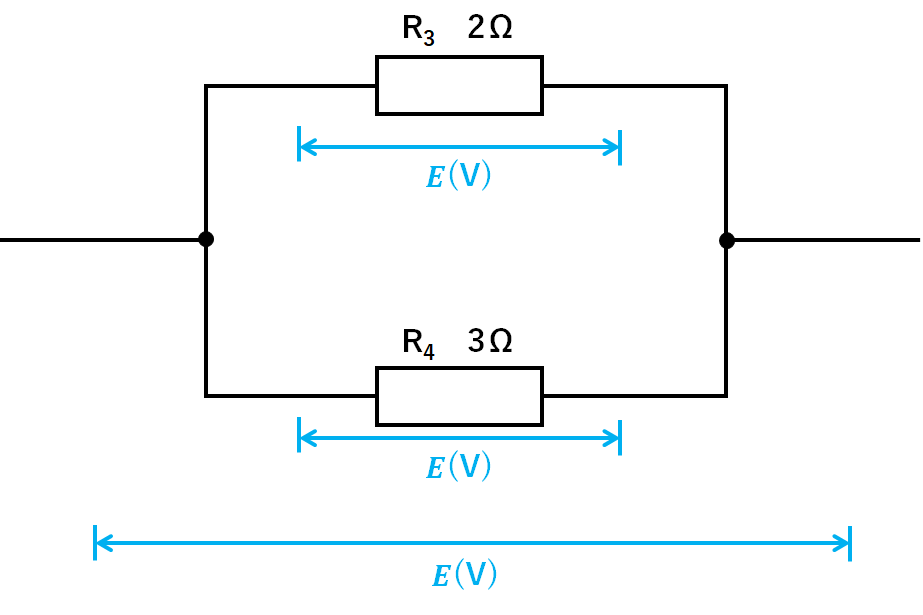
↓の図のように
$$R3の電圧=E(V)$$
$$R4の電圧=E(V)$$
ここでオームの法則を思い出しましょう。
$$電流(A)=\frac{電圧(V)}{抵抗(Ω)}$$
オームの法則を用いることで
$$R3の電流=\frac{E(V)}{2Ω}=\frac{E}{2}(A)$$
$$R4の電流=\frac{E(V)}{3Ω}=\frac{E}{3}(A)$$
であることがわかります。(↓の図)
ここで条件を振り返ってみましょう。
▼抵抗の比
$$R3の抵抗:R4の抵抗=2:3$$
▼電流の比
$$R1の電流:R2の電流=\frac{E}{2}:\frac{E}{3}=\frac{1}{2}:\frac{1}{3}=3:2$$
となります。
つまり並列回路では
抵抗の逆比=電流の比
となるのです。
※ここで注意点。逆比について。
2:3の逆比は3:2になります。
しかし逆比とは本来「ひっくり返す」ということではありません。
逆比の正確な意味は逆数の比ということです。
(逆数・・・分母と分子(上と下)を入れかえた数のこと)
2:3の逆比とは
$$\frac{1}{2}:\frac{1}{3}$$
のことです。
簡単な整数比になおすため、すべての項に6をかけて
$$\frac{1}{2}×6:\frac{1}{3}×6=3:2$$
となります。
たとえば1:2:3という3つの項から成る比があったとしましょう。
この逆比は3:2:1ではありません。
正しくは
$$\frac{1}{1}:\frac{1}{2}:\frac{1}{3}$$
とそれぞれの項の数を逆数にした比を書きます。
これを簡単な整数比に直すにはすべての項に6をかけて
$$\frac{1}{1}×6:\frac{1}{2}×6:\frac{1}{3}×6=6:3:2$$
となります。
POINT!
直列の場合・・・抵抗の比=電圧の比
並列の場合・・・抵抗の逆比=電流の比
3.抵抗の比を用いた例題
例題
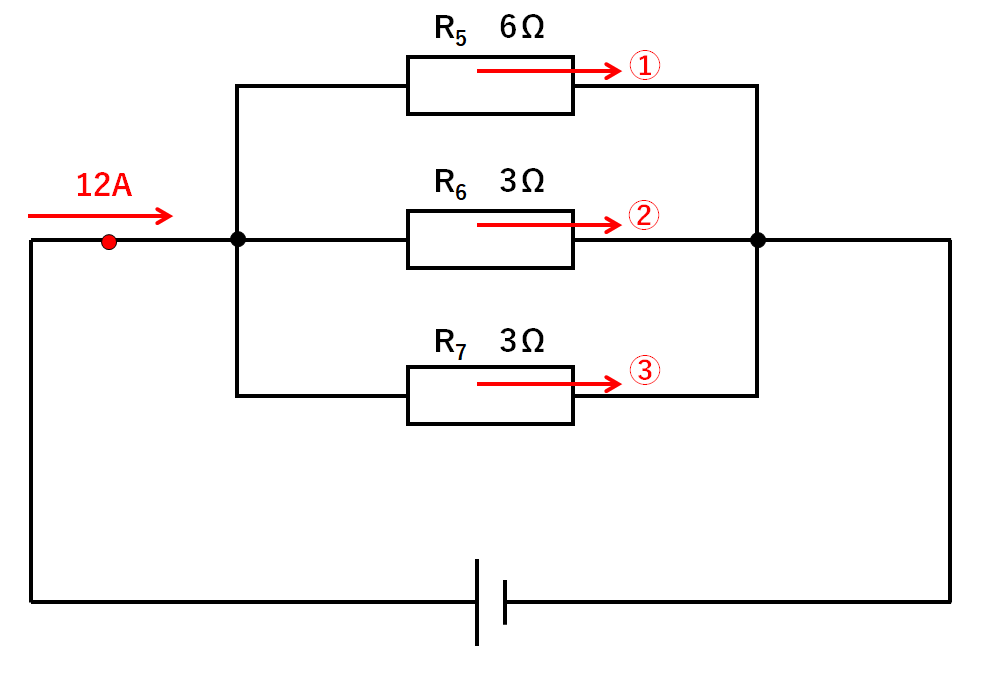
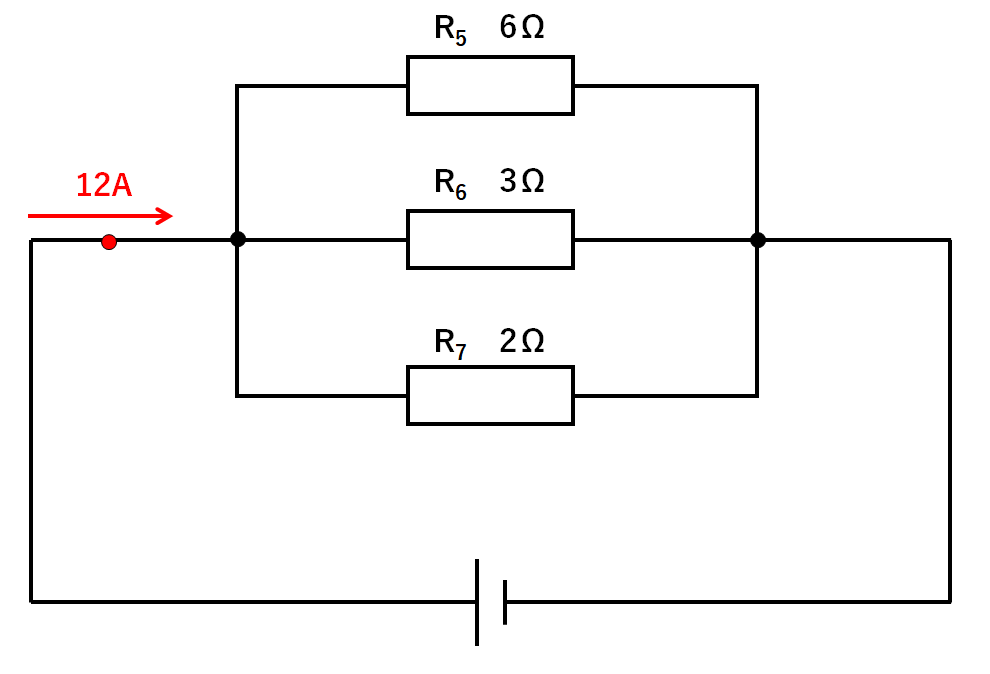
次のような回路でR5・R6・R7に流れる電流をそれぞれ求めよ。
(答)
解き方としては
①回路全体の抵抗(合成抵抗)を求める
②並列回路なので、抵抗の逆比=電流の比を使う
のどちらかとなります。
この場合は②の比を使う考え方をやってみましょう。
まず抵抗の比が
$$R5の抵抗:R6の抵抗:R7の抵抗=6:3:2$$
です。
電流はその逆比なので
$$R5の電流:R6の電流:R7の電流=\frac{1}{6}:\frac{1}{3}:\frac{1}{2}$$
簡単な整数比にすると
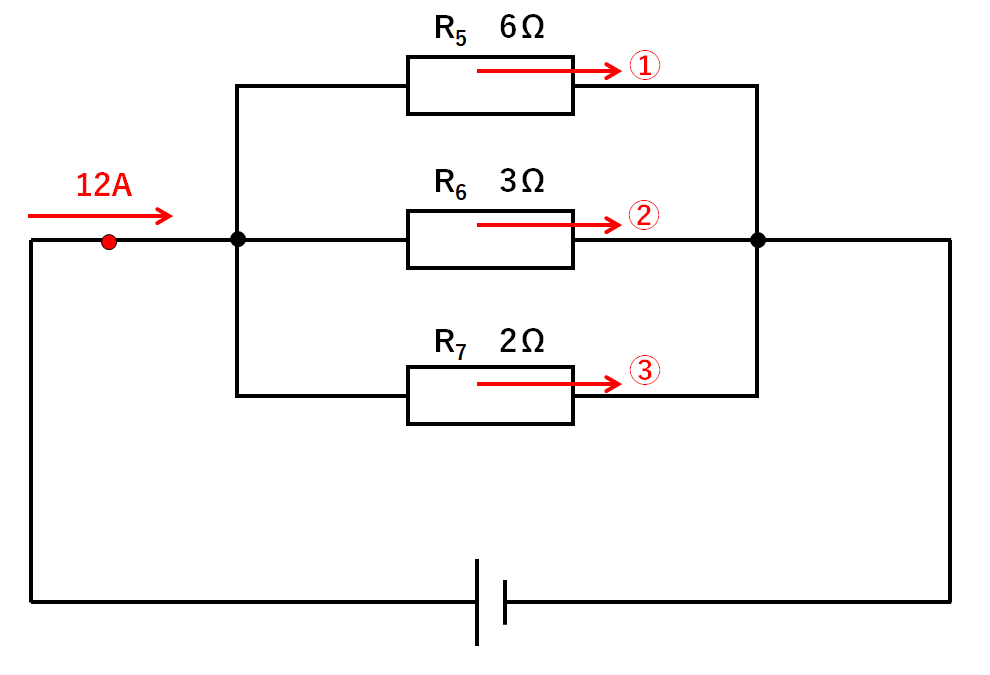
$$R5の電流:R6の電流:R7の電流=1:2:3$$
となります。(↓の図)
つまり枝分かれ前は12Aの電流だったものが1:2:3の割合で分かれていくのです。
よって
$$R5の電流=12A×\frac{1}{1+2+3}=2A$$
$$R6の電流=12A×\frac{2}{1+2+3}=4A$$
$$R7の電流=12A×\frac{3}{1+2+3}=6A$$
※R7の電流は12A-(2A+4A)=6Aと求めてもかまいません。
R5…2A R6…4A R7…6Aが正解となります。
4.抵抗比を応用してみよう
抵抗比を利用できるのはさきほどの回路の計算だけではありません。
熱量の問題においても利用ができます。
直列回路の場合
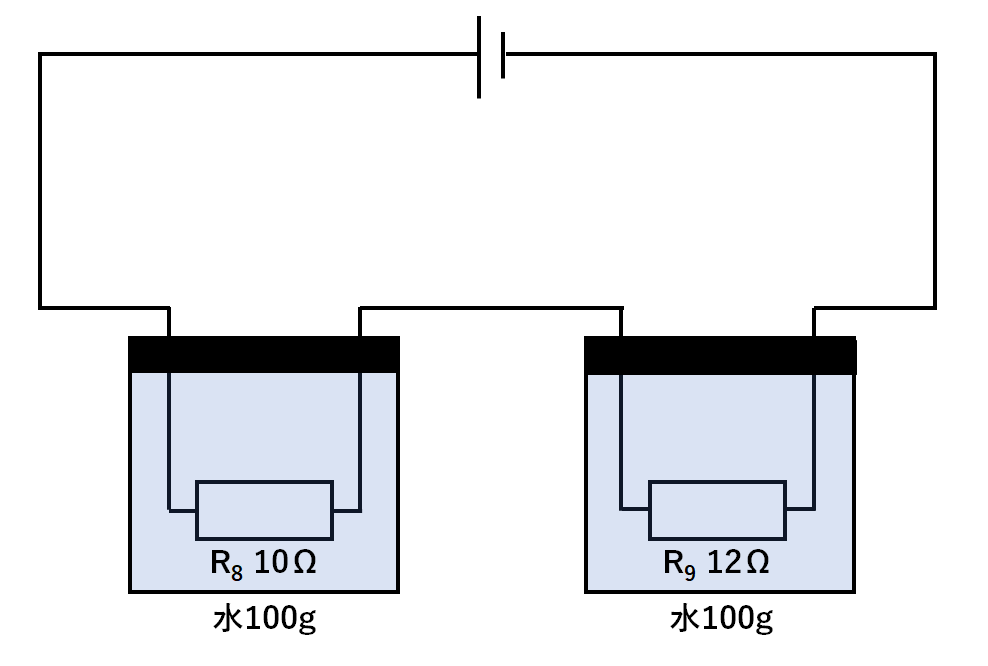
次のように、熱を伝えにくい容器に水と電熱線を入れ、その電熱線を直列につないだ回路があったとしましょう。
電熱線から発生する熱はすべて水の温度上昇のみに使われるとします。
この回路はR8とR9の直列回路です。
つまり抵抗の比=電圧の比です。
$$R8の抵抗:R9の抵抗=10:12=5:6$$
$$R8の電圧:R9の電圧=5:6$$
ここで
電圧×電流=電力
によって電力を求められますが
R8とR9に流れる電流の大きさは同じです。
つまりR8とR9での電力の比は、電圧の比と等しくなるはずです。
(例えばR8が5V・R9が6Vだとすると、その電圧にどんな電流をかけ算してもその比は5:6のままです)
よって
$$R8の電力:R9の電力=5:6$$
また熱量=電力×時間ですので
$$R8の熱量:R9の熱量=5:6$$
です。(R8とR9に電流が流れる時間は必ず同じ)
ということで水の上昇温度についても
$$左のビーカー:右のビーカー=5:6$$
となります。(水の量は同じなので)
よって直列回路の場合
抵抗の比=電圧の比=電力の比=熱量の比
となります。
並列回路の場合
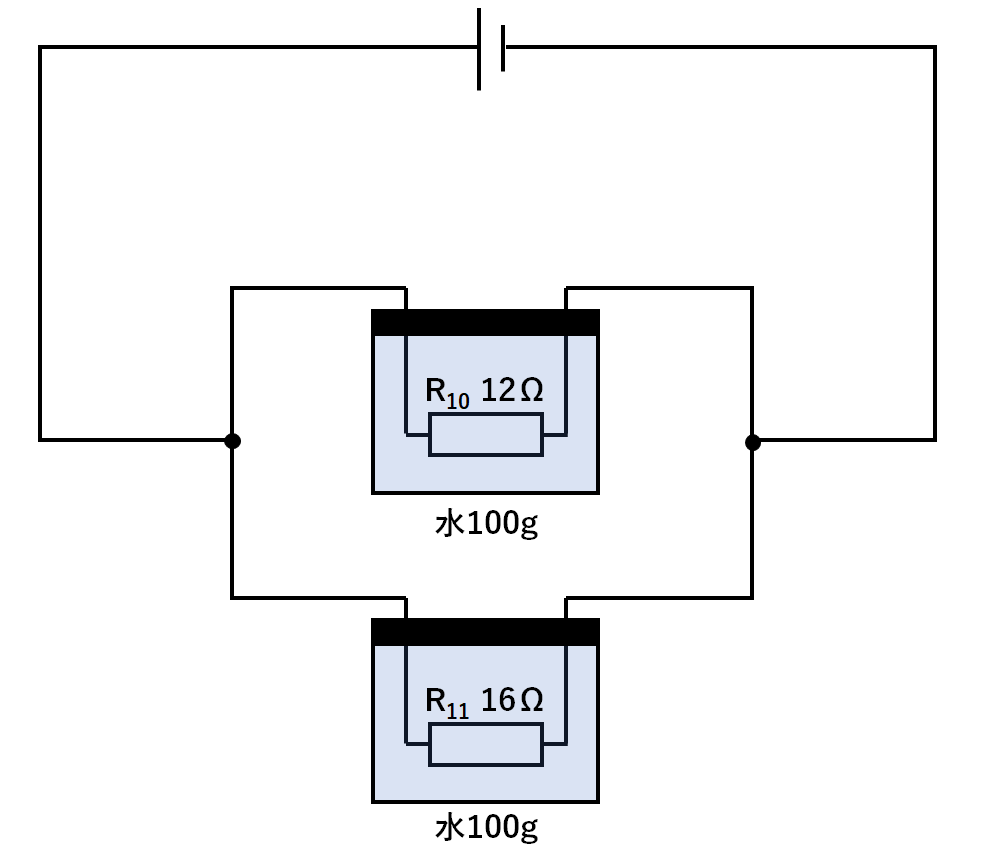
次のように、熱を伝えにくい容器に水と電熱線を入れ、その電熱線を並列につないだ回路があったとしましょう。
電熱線から発生する熱はすべて水の温度上昇のみに使われるとします。
この回路はR10とR11の直列回路です。
つまり抵抗の逆比=電流の比です。
$$R10の抵抗:R11の抵抗=12:16=3:4$$
$$R10の電流:R11の電流=4:3$$
ここで
電圧×電流=電力
によって電力を求められますが
R10とR11に加わる電圧の大きさは同じです。
つまりR10とR11での電力の比は、電流の比と等しくなるはずです。
よって
$$R10の電力:R11の電力=4:3$$
また熱量=電力×時間ですので
$$R10の熱量:R11の熱量=4:3$$
です。(R10とR11に電流が流れる時間は必ず同じ)
ということで水の上昇温度についても
$$上のビーカー:下のビーカー=4:3$$
となります。(水の量は同じなので)
よって並列回路の場合
抵抗の逆比=電流の比=電力の比=熱量の比
となります。
・直列回路・・・抵抗の比=電圧の比=電力の比=熱量の比
・並列回路・・・抵抗の逆比=電流の比=電力の比=熱量の比
公立入試であってもこれが使えることは重要。
公立入試の最も難度が高い問題は、このテクニックを駆使できれば余裕でとけるはず。
難関高校を目指す場合は、普段の回路の計算からこれを使いこなすことが重要。
合成抵抗でも代用できるケースが多いですが、本当にできる子というのは両方を使いこなします。

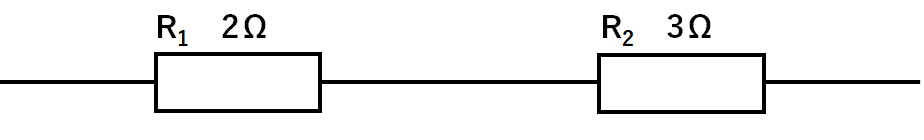
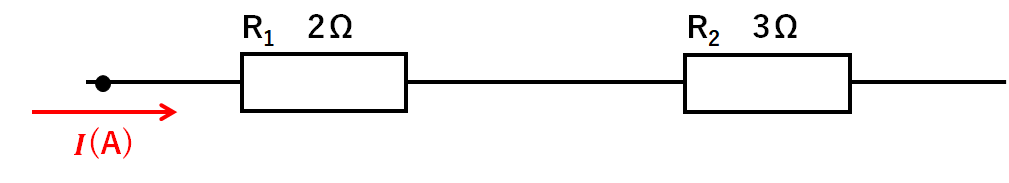
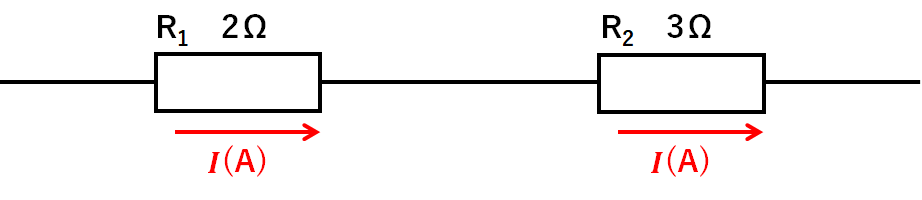
コメント(承認された場合のみ表示されます)