中2物理【熱の出入りについての問題】

このページでは「cal」をつかった計算や「電熱線から発生した熱によって水の温度が上がる」という問題の解説をしています。

少し発展的な内容を含んでいます。

熱量の基本的な考え方は→【熱量・電力量】←を読んでみてください。

動画による解説はこちら↓↓↓（calについては触れていません）

https://youtu.be/bGfrWhu2ffQ

チャンネル登録はこちらから↓↓↓

1．水の温度の上がり方

cal（カロリー）とは熱量の単位です。熱量の単位にはJ（ジュール）の単位もあります。

「cal」と「J」の関係は1cal=約4.2Jです。

（1J=0.24calとなっている場合もあります。）

つまり水1gの温度を1℃上げるのに必要な熱量は約4.2Jとも言えます。

例えば、水300gの温度を4℃上昇するのに必要な熱量は

$$300g×4℃=1200cal$$

となります。

ここで問題に「1cal=4.2J」を利用すれば

$$1200cal=1200×4.2=5040J$$

と単位を「cal」から「J」へと変換することもできます。

例えば水70gの温度を10℃上昇させるのに必要な熱量は

$$70g×10℃=700cal$$

であり、「1cal=4.2J」を用いると

$$700cal=700×4.2=2940J$$

とも求めることができます。

2．熱の出入りに関する問題

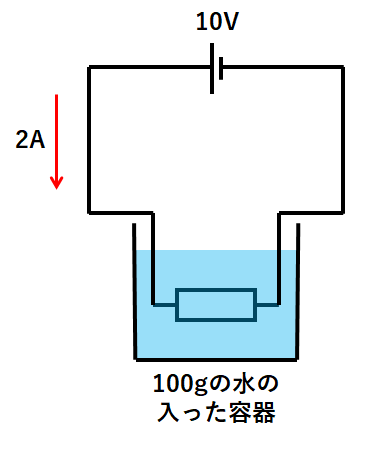
次のような回路で容器内の水を温めることを考えます。

このとき水の温度は何℃上がるか考えてみましょう。

例題

(答)

まず電熱線から出る熱量を求めます。

電熱線から出る熱量は

$$熱量(J)=電力(W)×時間(s)$$

で求められます。

電力の公式から

$$電力(W)=電流(A)×電圧(V)=10V×2A=20W$$

そして熱量の公式から

$$電熱線から出た熱量(J)=電力(W)×時間(秒)=20W×840秒=16800J…①$$

となります。

次に

水の温度がx℃上昇する

として水に入った熱量を求めましょう。

$$水に入った熱量(cal)=水の量(g)×上昇温度(℃)=100g×x(℃)=100x(cal)$$

と表すことができます。

1cal=4.2Jとしているので

$$100x(cal)×4.2=420x(J)…②$$

となります。

ここで「電熱線から発生した熱量は水の温度上昇のみに使われる」という注意書きがあるため、①と②は等しいことになります。

①=②という方程式をつくります。

$$16800(J)=420x(J)$$

これを解いて

$$x=40$$

つまり

水温が40℃上昇することになります。

これが答えです。

注意しておきたいこと

ここで非常に大切な注意点です。

先ほどの例題では「電熱線から発生した熱量は水の温度上昇のみに使われる」としました。

しかし現実世界ではこんなにうまくいきません。

「電熱線から発生した熱量は水の温度上昇のみに使われる」ことはないからです。

電熱線から発生した熱量の一部は空気中へ逃げたり、容器の温度上昇に使われたりしますから。

そのため問題によっては

「電熱線から発生した熱量のうち30％が水の温度上昇に使われる」

なんて注意書きがあることもあります。

「電熱線から発生した熱のすべてが水の温度上昇に使われる」のか

「電熱線から発生した熱の一部が水の温度上昇に使われる」のか

これは大きな違いです。

実際に問題を解くときはこの注意書きに気を付けましょう。

例題2

(答)

電熱線から出た熱量を求めます。

$$電熱線から出た熱量=電力(W)×時間(秒)$$

$$=15V×4A×100秒=6000J$$

次に水500gの温度が2℃上がったことから、水に入った熱量を求めます。

$$水に入った熱量(cal)=水の量(g)×上昇温度(℃)$$

$$500g×2℃=1000cal$$

1cal＝4.2Jであるので1000calをJの単位に変換します。

$$1000cal×4.2=4200J$$

電熱線から出た熱量6000Jのうち、水に入ったのは4200Jです。

ということは

$$6000J-4200J=1800J$$

の1800Jの熱量は水に入らなかったことになります。

つまり逃げた熱量は1800Jといえます。

この問いは発生した熱のうち、一部が水に入ったという問題の例でした。