このページでは、熱量の計算や「J(ジュール)・Wh(ワット時)」について解説しています。
また水を温めたときの温度変化を考える問題についても解説。
このページの単元を理解するには →【オームの法則】← と →【電力】← の単元をできるようにしておきましょう。
動画による解説は↓↓↓
チャンネル登録はこちらから↓↓↓
1.熱量
熱エネルギーの量のこと。単位は【J】(ジュール)を用います。
※エネルギーの単位はすべて【J】です!
※電気器具から発生した熱エネルギーの量を特に”発熱量”といいます。
電熱線とは、電流を流すと熱が発生する電気器具です。
ここでは電熱線から発生した熱量を考えます。
$$電熱線から出る熱量(J)=電力(W)×時間(秒)$$
電力は「1秒あたりにどれだけのエネルギーを出すことができるか」という意味です。
「3W」というのは「1秒あたりに3Jのエネルギーを出すよ」ということです。
そのため電熱線の使用時間を掛け算すれば熱量(熱エネルギーの量)を求めることができます。
※「秒数」をかける、ということに注意!「分」ではありません。
2.水を温める
この単元では、容器に水と電熱線を入れて水を温めるというお話がたくさん出てきます。
水の温度は電熱線から発生した熱によって上がります。
電熱線から発生した熱がすべて水の温度上昇に使われるとき、水の上昇温度は熱量に比例します。
(ちなみに水の量には反比例します。)
どういうことか次の例題で確認してみます。
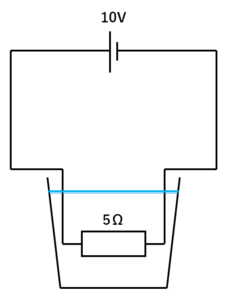
例題
このとき水の温度が2℃上がった。
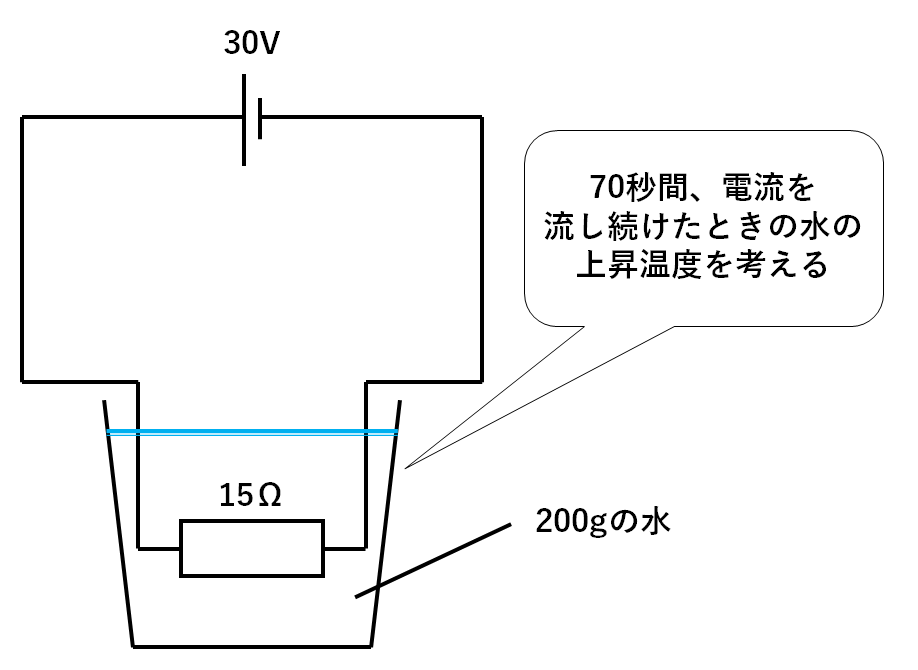
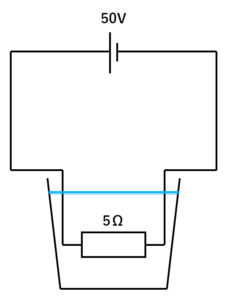
このとき次の図2の回路では、水の温度は何℃上がるか?
ただし電流を流す時間や水の量は図1と同じとする。
(答)
まず、図1の場合に電熱線から発生する熱量を計算します。
オームの法則より
$$電流(A)=\frac{電圧(V)}{抵抗(Ω)}=\frac{10V}{5Ω}=2A$$
電力の公式から
$$電力(W)=電流(A)×電圧(V)=2A×10V=20W$$
先ほど紹介した熱量の公式より
$$電熱線から出る熱量(J)=電力(W)×時間(秒)=20W×600秒=12000J$$
よって12000Jです。
次に図2の場合にで電熱線から発生する熱量を計算します。
オームの法則より
$$電流(A)=\frac{電圧(V)}{抵抗(Ω)}=\frac{50V}{5Ω}=10A$$
電力の公式より
$$電力(W)=電流(A)×電圧(V)=10A×50V=500W$$
先ほど紹介した熱量の公式より
$$電熱線から出る熱量(J)=電力(W)×時間(秒)=500W×600秒=300000J$$
よって300000Jです。
図2の電熱線から出る熱量は30000J。
図1の電熱線から出る熱量は12000J。
$$300000J÷12000J=25倍$$
図2では図1の25倍の熱量が発生しているということになります。
よって、図2での水の上昇温度も図1の25倍。
図1の水の上昇温度は2℃であるため
$$図2の水の上昇温度=2℃×25=50℃$$
ということになります。
図2の水の上昇温度は50℃です。
3.電力量
■電力量
電力に時間をかけたものです。
時間を【秒】(s)の単位でかけ算するか、【時間】(h)の単位でかけ算するかでその単位が違います。
$$電力量【Wh(ワット時)】=電力【W】×時間【時間】$$
$$電力量【J】=電力【W】×時間【秒】$$
ここは公式を覚えるだけでOK。
(【Wh】で「ワット時」と読みます。)
電力量と熱量にほとんど違いはありません。
・「何Jですか」という問いか
・「何Whですか」という問いか
どの単位を問われているかでやや求め方が異なるので、問題文をよく読みましょう。
POINT!!
・「J=W×秒」を覚えておこう。
・「水温上昇」は「電力」で考えると楽なことが多い。
こちらもどうぞ
このページで解説している「熱量」「電力量」に関する計算ドリルを販売中です。
PDF形式のダウンロード販売です。
1つ220円(税込)です。
よければどうぞ。



コメント(承認された場合のみ表示されます)
熱量と電力量って何が違うんですか。求める式は同じなのに何が変わるんですか。
理科わかりません様
コメントありがとうございます。
電気器具(電球やポットなど)を作動させるのに、電気が必要です。
この電気器具を作動させるのに使った電気エネルギーが「電力量」です。
一方で、作動させた結果、電球であれば光エネルギーが発生します。
ポットであれば熱エネルギーが発生します。
「熱を発生させる電気器具」に注目したときに、いくらの熱エネルギーが発生したかが「(発)熱量」です。
↓のようなイメージです。
わかりやすかったです🤍
愛@_itoshi.様
コメントありがとうございます。
お役に立てたならば幸いです。
また是非ご利用ください。