中2物理【*非オーム抵抗】

このページには教科書内容を超えた発展的な内容が含まれます。

1．非オーム抵抗

 

中学理科でよく出てくる電熱線の多くはニッケルクロム線（ニクロム線）と呼ばれます。

このニクロムという物質は、加える電圧を大きくすると流れる電流も大きくなります。

つまりオームの法則が成り立つ物質なんですね。

そのため、電圧と電流の関係をグラフにすると直線（比例の関係）になります。

 

グラフのどの場所で計算しても抵抗値は一定になります。

これが中学校の理科の「オームの法則」のお話しです。

 

しかし、世の中の金属がすべて「オームの法則が成り立つ」わけではありません。

例えばタングステンという物質。

電球に使われる金属です。

 

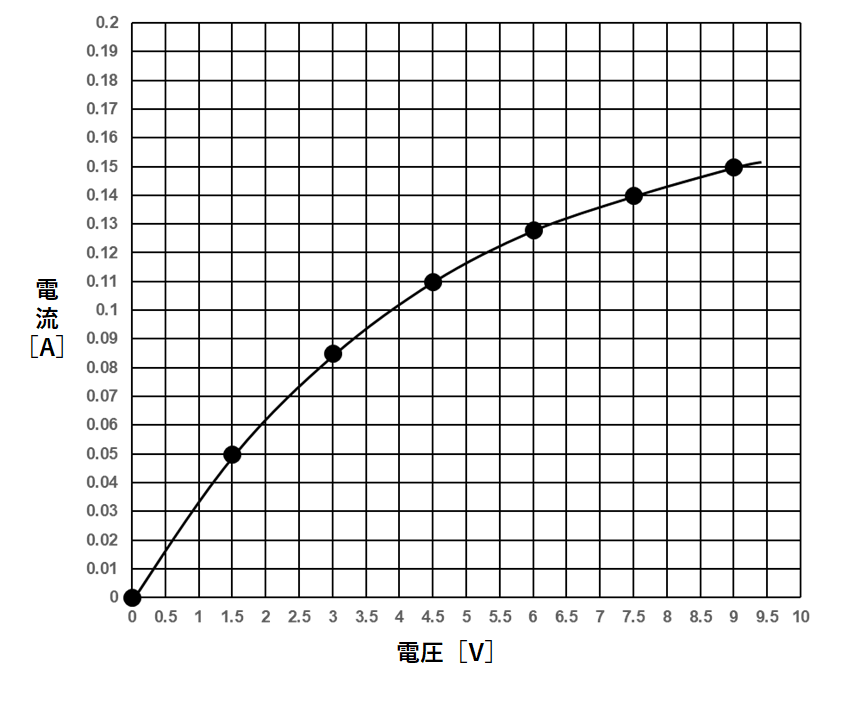
タングステンに加わる電圧と電流の関係をグラフにすると↓のようになります。

まっすぐな「比例」のグラフではありません。

これはオームの法則が成り立たず、抵抗値が一定ではないことを表します。

 

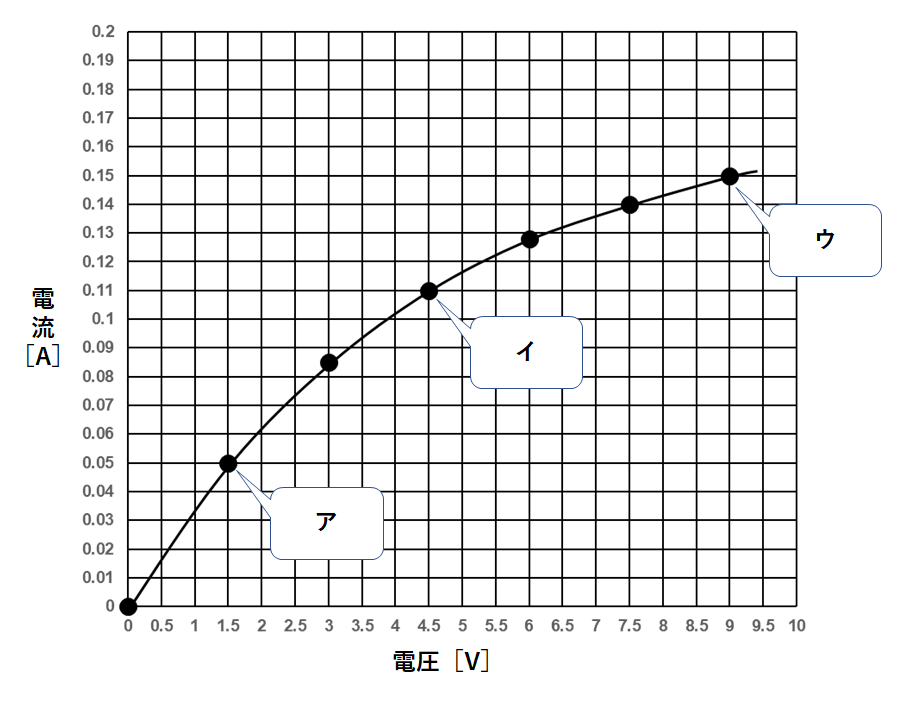
例えばア～ウの各点における抵抗値を計算してみましょう。

$$抵抗(Ω)=\frac{電圧(V)}{電流(A)}$$

を使います。

 

アの場合は

$$\frac{1.5V}{0.05A}=30Ω$$

 

イの場合は

$$\frac{4.5V}{0.11A}=40.90・・・≒約41Ω$$

 

ウの場合は

$$\frac{9V}{0.15A}=60Ω$$

 

このようにタングステンでは、抵抗値が一定ではありません。

このような関係を示す抵抗のことを非オーム抵抗（非線形抵抗）といいます。

(言葉までは覚える必要はありません)

 

大切なのは、抵抗が一定ではないということです。

 

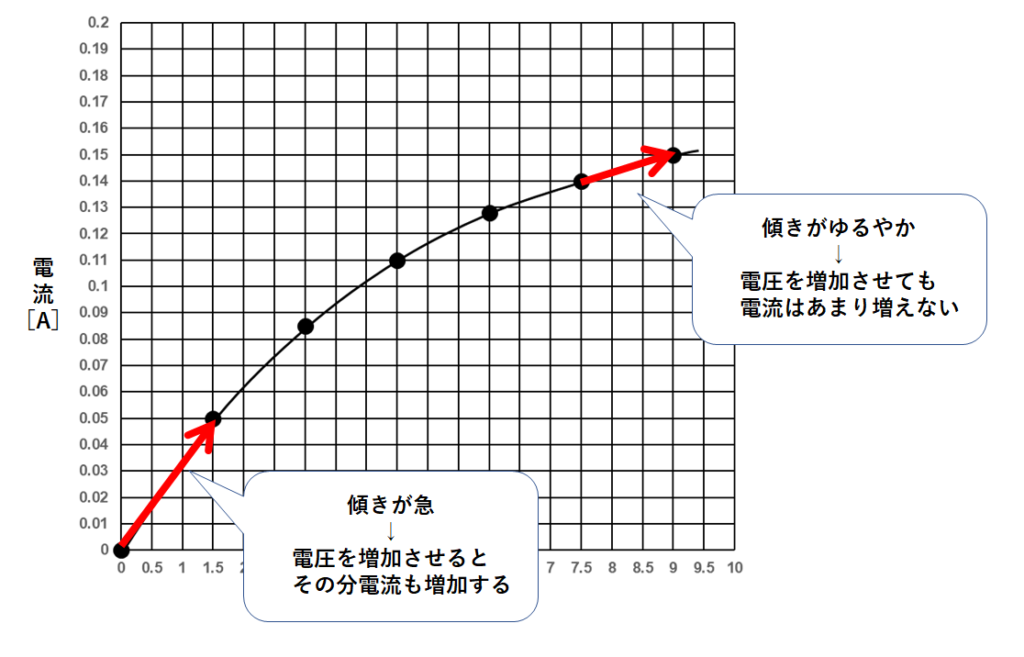
非オーム抵抗の特徴は

ア(30Ω)→イ(41Ω)→ウ(60Ω)

と電圧を大きくするほど抵抗値が大きくなるというところです。(↓の図)

 

 

2．非オーム抵抗の問題

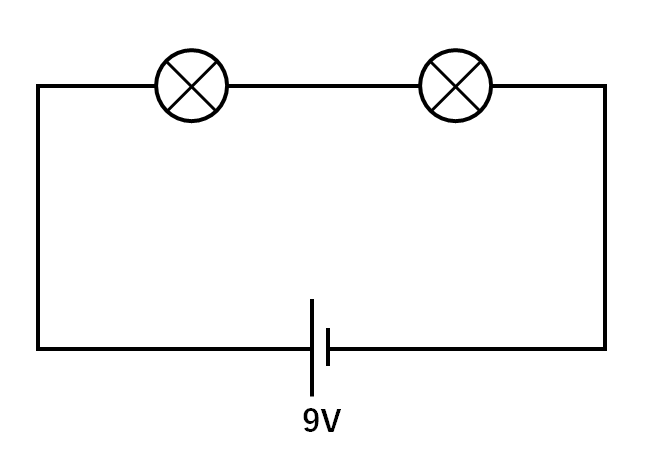
例題1

例題1　答えと解説

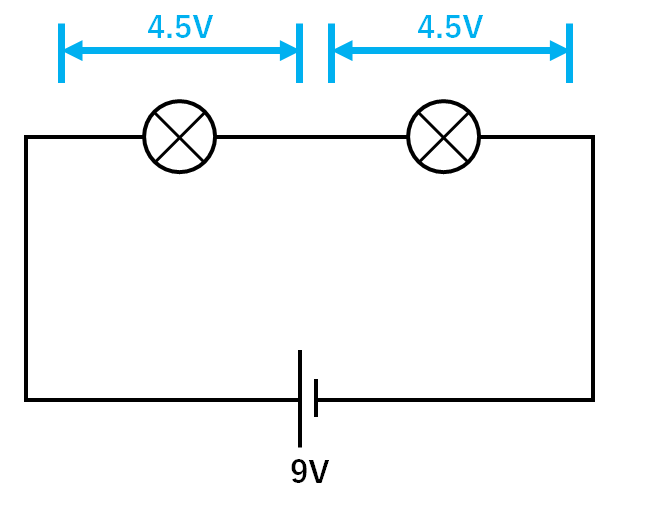
同じ豆電球が2つ直列につながれているので、加わる電圧は4.5Vずつになります。(↓の図)

ここで、豆電球にかかる電圧が4.5Vのときの電流を、グラフから読み取ります。

よって0.11Aが正解となります。

 

 

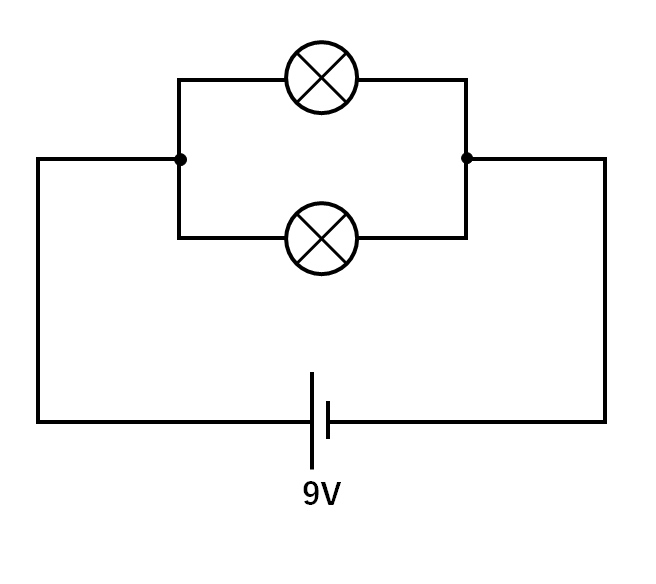
例題2

 

例題2　答えと解説

この豆電球は並列につながれています。

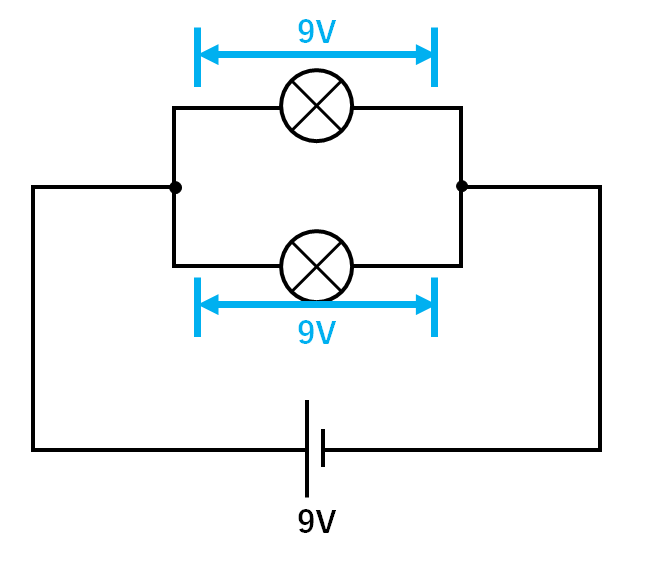
そのため1つの豆電球に加わる電圧は9Vです。(↓の図)

ここで豆電球に9Vの電圧が加わっているときに流れる電流を、グラフから読み取ります。

よって豆電球1個あたりには0.15Aが流れます。

（回路全体では0.15A×2＝0.3Aの電流です。）

 

 

非オーム抵抗に関するもっとも難しい問題は次の例題です。

これは高校物理のレベルなので、中学生の間は解けなくてもよいと思います。

 

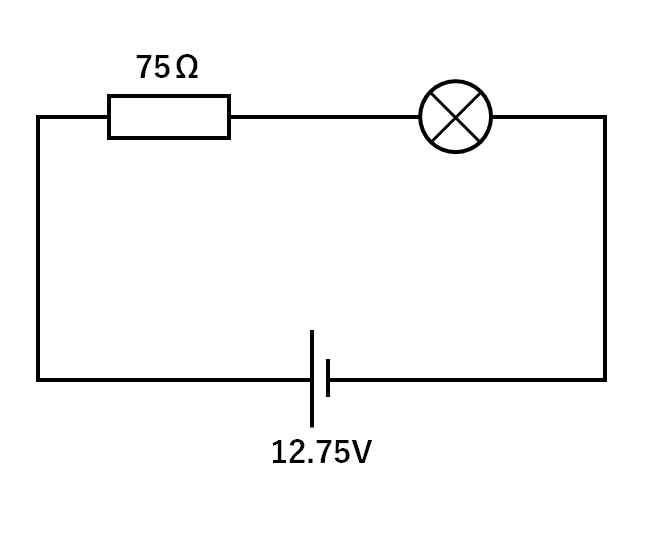
例題3　*難しい

 

例題3　答えと解説

これは非常に難しい問題です。

 

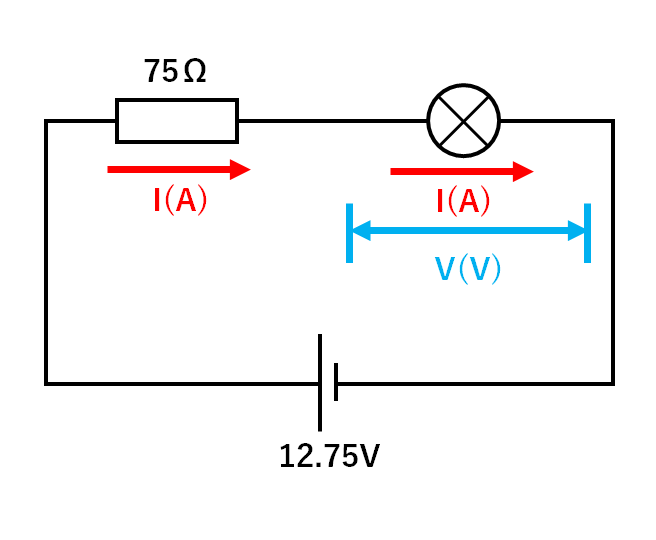
まず豆電球に流れる電流をI(A)、豆電球に加わる電圧をV(V)としましょう。(↓の図)

75Ωの電熱線に流れる電流もI(A)です。(↓の図)

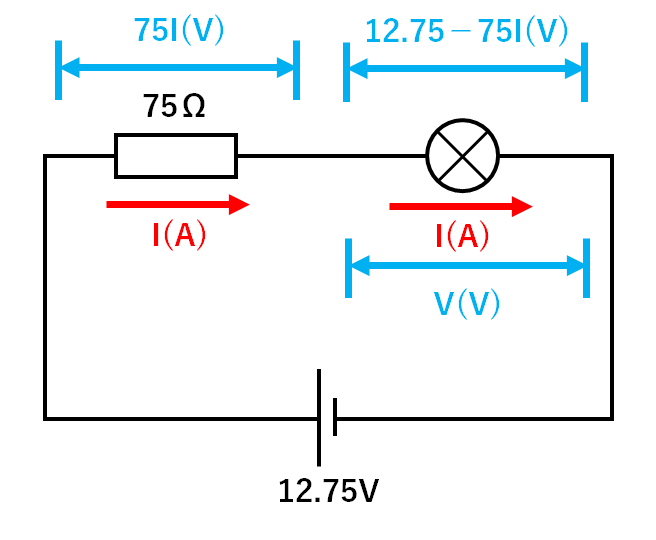
すると75Ωの電熱線に加わる電圧は

$$75I(V)$$

と表すことができます。

 

電源電圧が12.75Vなので、豆電球に加わる電圧は

$$12.75-75I(V)$$

と表せます。(↓の図)

 

よって

$$V=12.75-75I(V)$$

の関係があります。

 

この式を　I=・・・　の形に変形します。

$$75I=-V+12.75$$

$$I=-\frac{V}{75}+\frac{12.75}{75}$$

$$I=-\frac{V}{75}+0.17$$

 

このIとVは一次関数の関係になっています。

IとVなのでわかりにくいですが、xとyに置き換えると

$$y=-\frac{x}{75}+0.17$$

となりますので、xの一次関数と言えます。

 

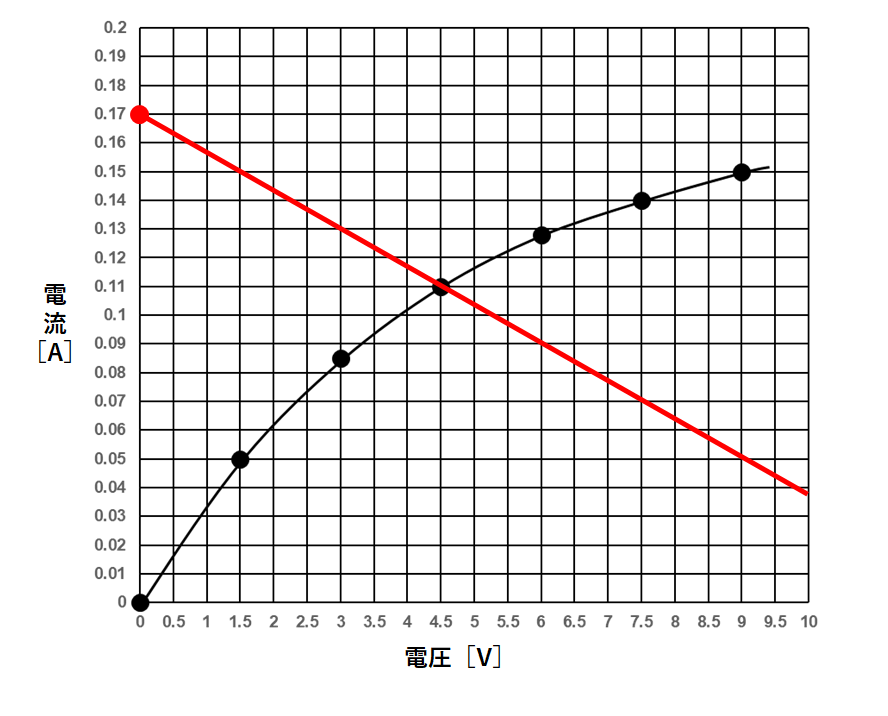
そのグラフを書いてみます。(↓の図)

 

ここでグラフの交点を見ます。

交点の値が、豆電球の電圧と電流を表すのです。

 

よって豆電球に流れる電流は0.11Aとなります。