中3物理【力学的エネルギーの保存】

このページでは「位置エネルギーとは」「運動エネルギーとは」「位置エネルギー・運動エネルギーの求め方」「力学的エネルギーの保存（保存の法則）」について解説しています。

動画による解説は↓↓↓

チャンネル登録はこちらから↓↓↓

1．エネルギーとは

エネルギーとは何か。これはとてもとても難しい話です。

以下の点だけを押さえておこう。

 

エネルギーを持っている物体は

・ほかの物体を動かすことができる。

・ほかの物体を変形させることができる。

・ほかの物体を壊すことができる。

 

このような状態にある物体を「エネルギーを持っている」と言います。

エネルギーの単位は【J】(ジュール)。

 

2．位置エネルギー

 

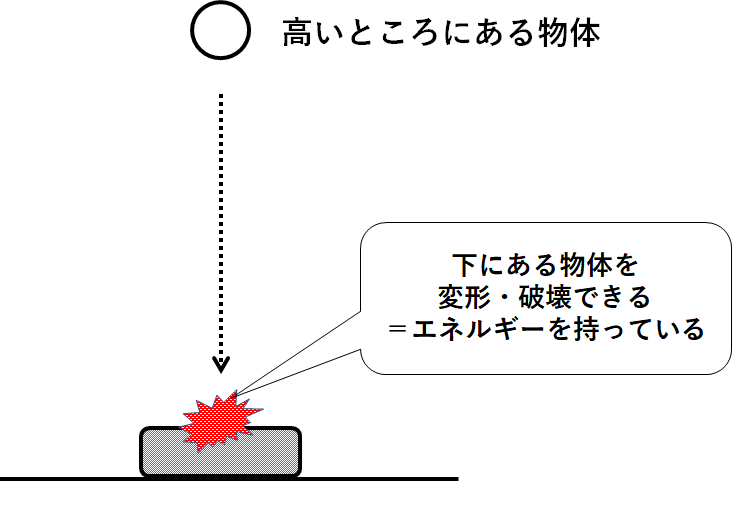
たとえば高いところに鉄球があって、その下には車があったとしましょう。

この鉄球を落下させると、当然の下の車は破壊されます。

つまり車を破壊できるので鉄球はエネルギーを持っています。

 

正しく言うと高いところにある鉄球はエネルギーを持っているわけです。

 

 

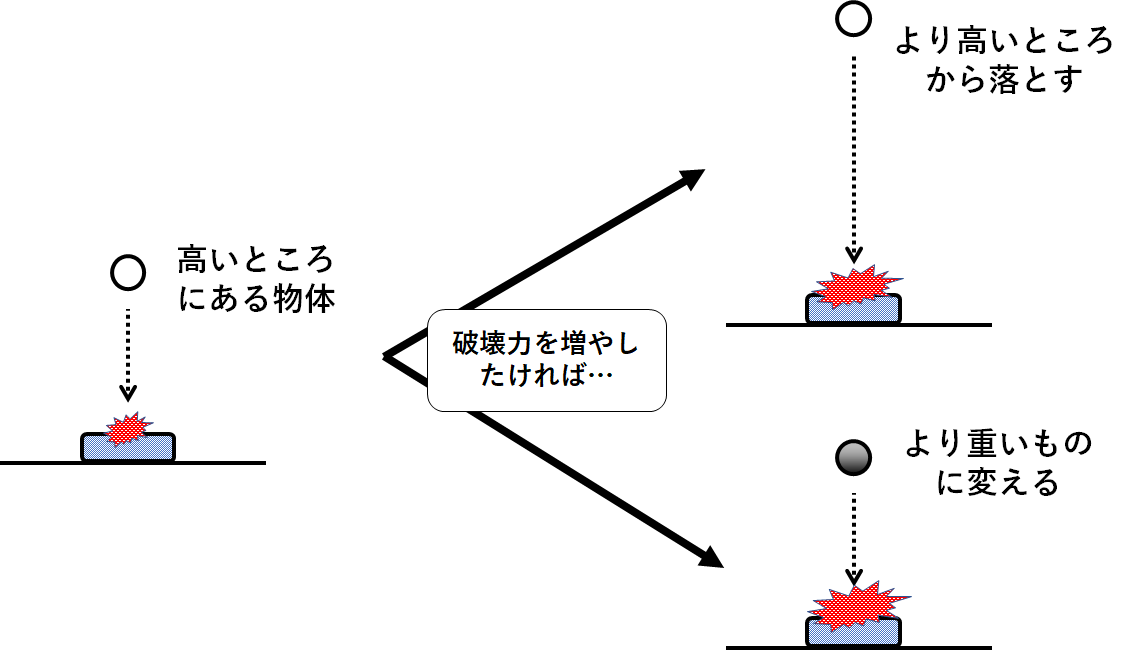
ではこの鉄球の破壊力を大きくするには？

・より重い鉄球に変えること。

・重さを変えずともより高い位置から落としてやればいい。

 

 

つまり、この鉄球の持つエネルギーは「重さ」と「高さ」によって変化するわけです。

「高さ＝位置」によって決まるエネルギーなので、これを位置エネルギーと言います。

 

位置エネルギーは重さに比例し、高さにも比例します。

 

よって次の式で求められます。

$$位置エネルギー(J)＝重さ(N)×高さ(m)$$

こちらの式は必ず覚えておきましょう。

3．運動エネルギー

 

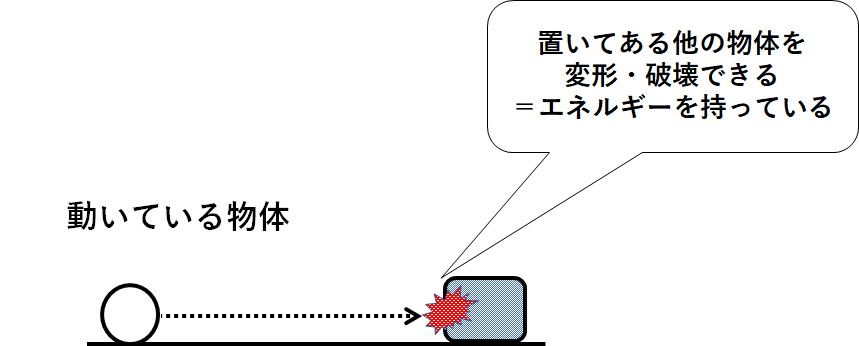
鉄球をボーリングのように転がして車にぶつけることを考えてみましょう。

鉄球がぶつかると車は破壊・変形されます。

つまり動いている鉄球というのはそれだけでエネルギーを持っているということ。

 

 

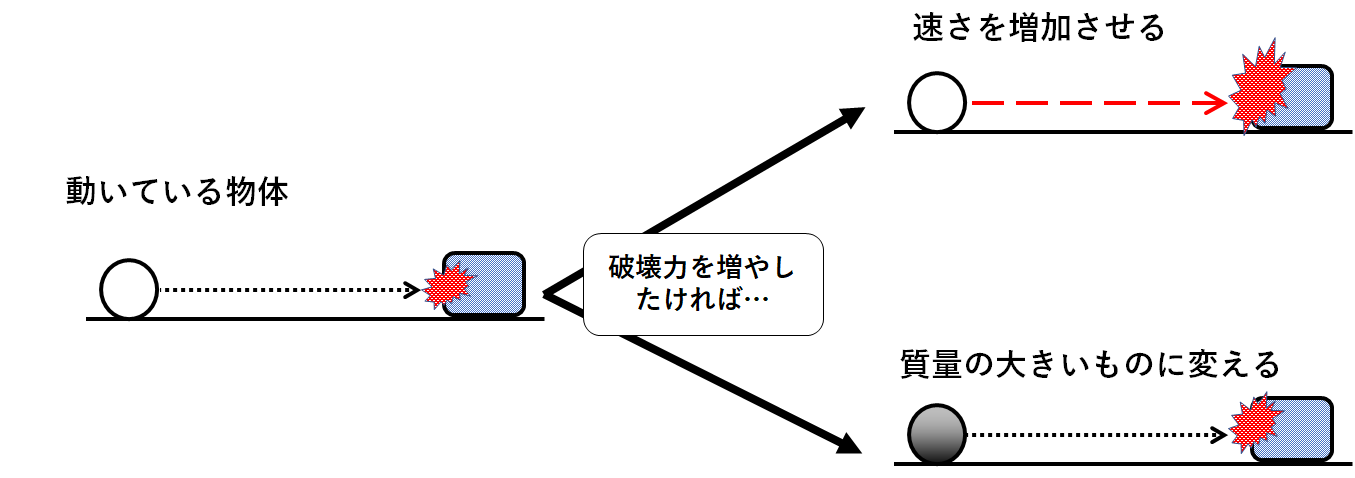
ではこの場合の鉄球の破壊力を大きくするには…

・より質量の大きな鉄球でぶつけること。

・質量は変えず、思いっきり勢いをつけてぶつける。

⇒　つまり、速さを大きくしてぶつけるということ。

 

このように動いている鉄球の持つエネルギーは「質量」と「速さ」によって変化します。

「速さ＝その物体の動き」によって決まるエネルギーなので、これを運動エネルギーと言います。

運動エネルギーは質量に比例・速さの2乗に比例します。

 

 

※運動エネルギーにも公式があります。

ただし高校入試ではあまり使うことはありません。余裕があれば覚えておきましょう。

$$運動エネルギー(J)＝\frac{1}{2}×質量(kg)×速さ(m/s)×速さ(m/s)$$

4．力学的エネルギー保存の法則

 

 

力学的エネルギーは位置エネルギーと運動エネルギーの和です。

この力学的エネルギーは運動の最中、常に一定になります。

 

※ただし運動のようすを変えるような力・・・「摩擦力」「空気抵抗」がはたらいていなければという条件付き。

 

このきまりを力学的エネルギーの保存、または力学的エネルギー保存の法則と言います。

 

力学的エネルギーの保存の使い方

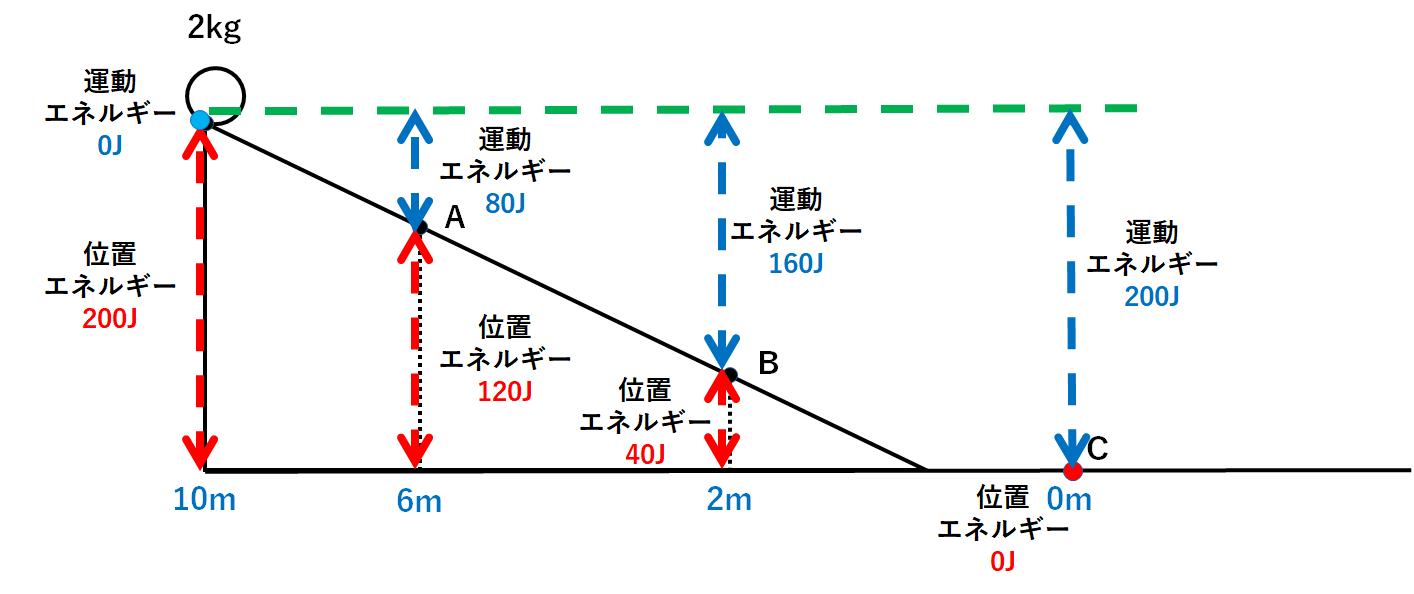
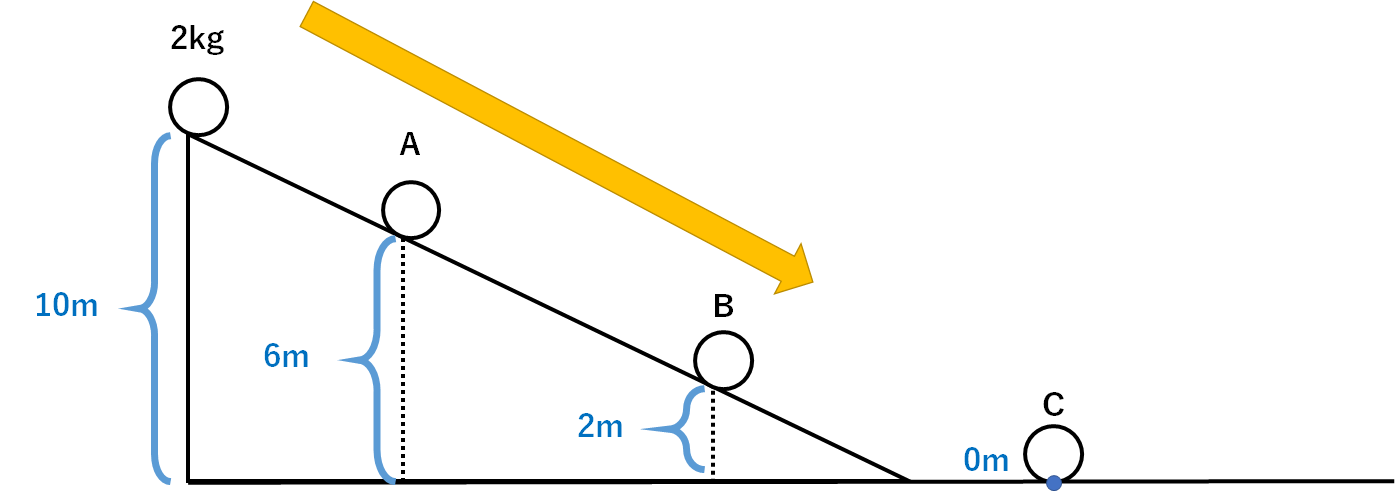
↓の図のようなコースを質量2kgの物体が進んでいくとしましょう。

ここでは摩擦や空気抵抗は考えないものとします。

10mの高さから、2kgの小球を静かに手を離しすべらせます。

 

 

ここからA点・B点・C点を通過したときのエネルギーを考えます。

①スタート地点

高さは10mです。

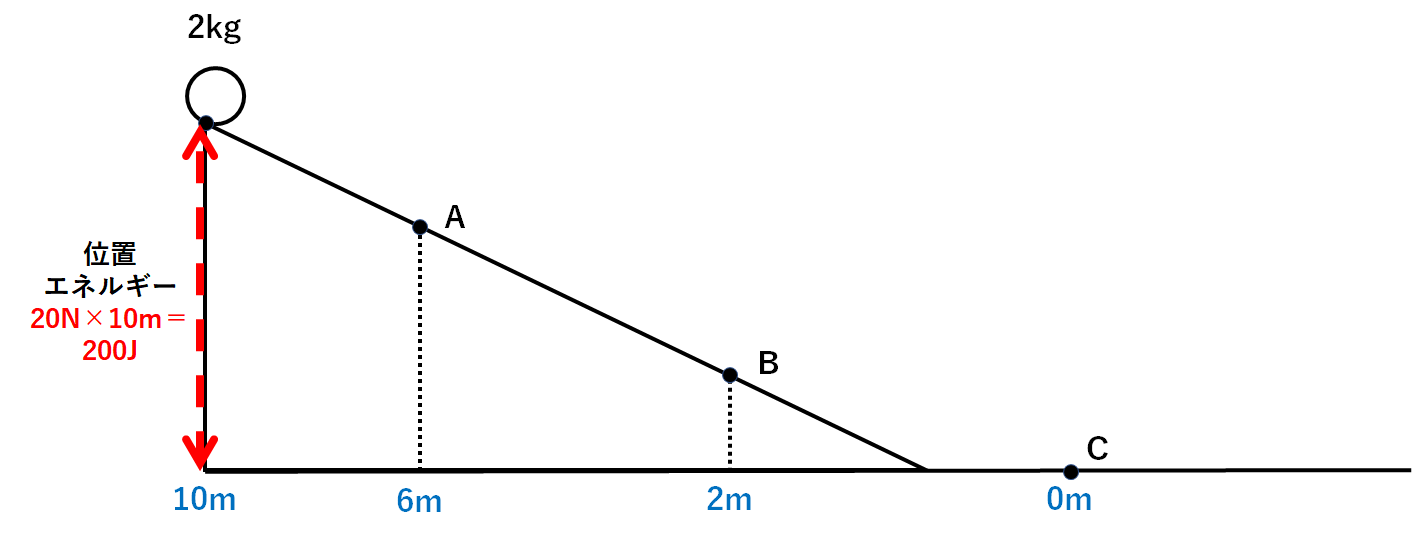
ここで位置エネルギーの公式を使うと

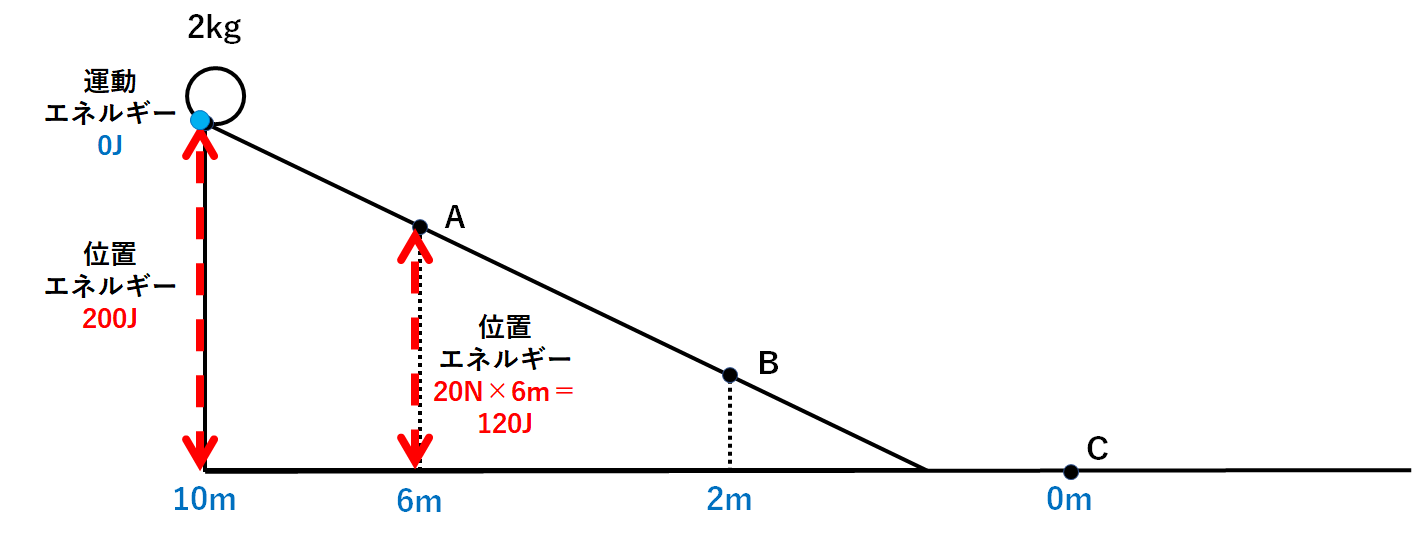
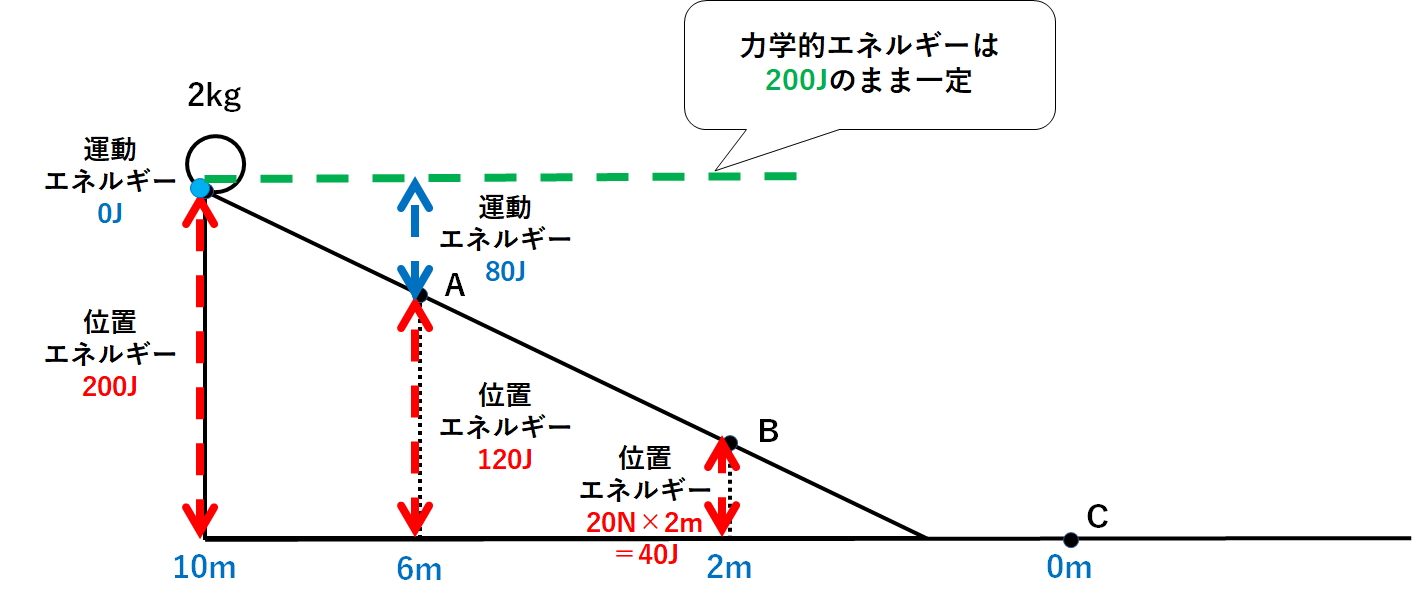
スタート地点の位置エネルギー＝20N×10m＝200J

とわかります。(↓の図)

 

ここでは手を放した瞬間なので、速さはゼロです。

 

つまり

運動エネルギー＝0J

です。

 

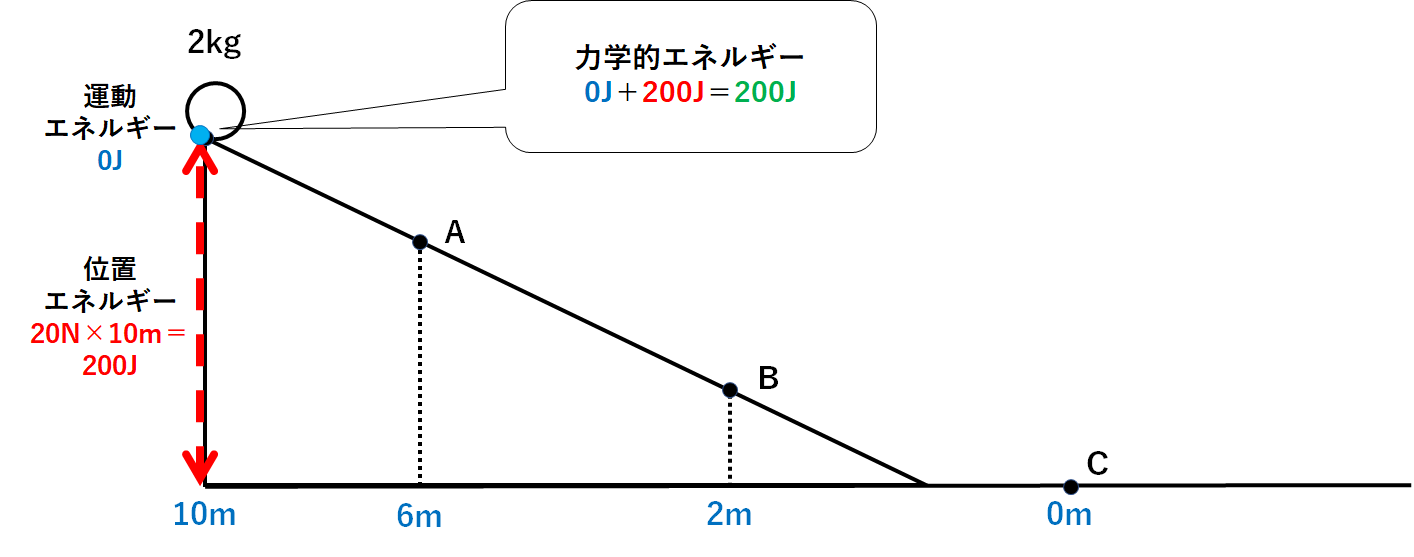
よって

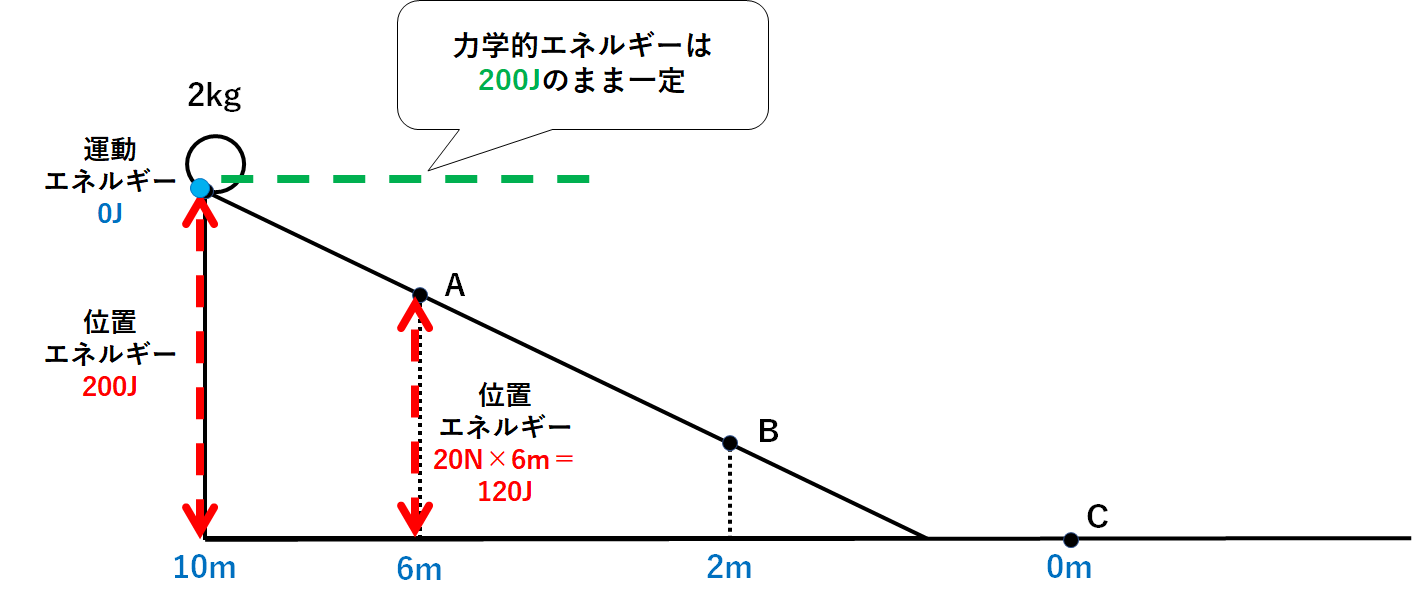
力学的エネルギー＝位置エネルギー＋運動エネルギー＝200J

とわかります。（↓の図）

 

 

この後、力学的エネルギーの保存という決まりによって力学的エネルギーは200Jのまま保存されます。（変化しない）

 

②A点を通過した瞬間

A点は6mの高さなので

位置エネルギーの公式を使うと

A点での位置エネルギー＝20N×6m＝120J

となります。(↓の図)

 

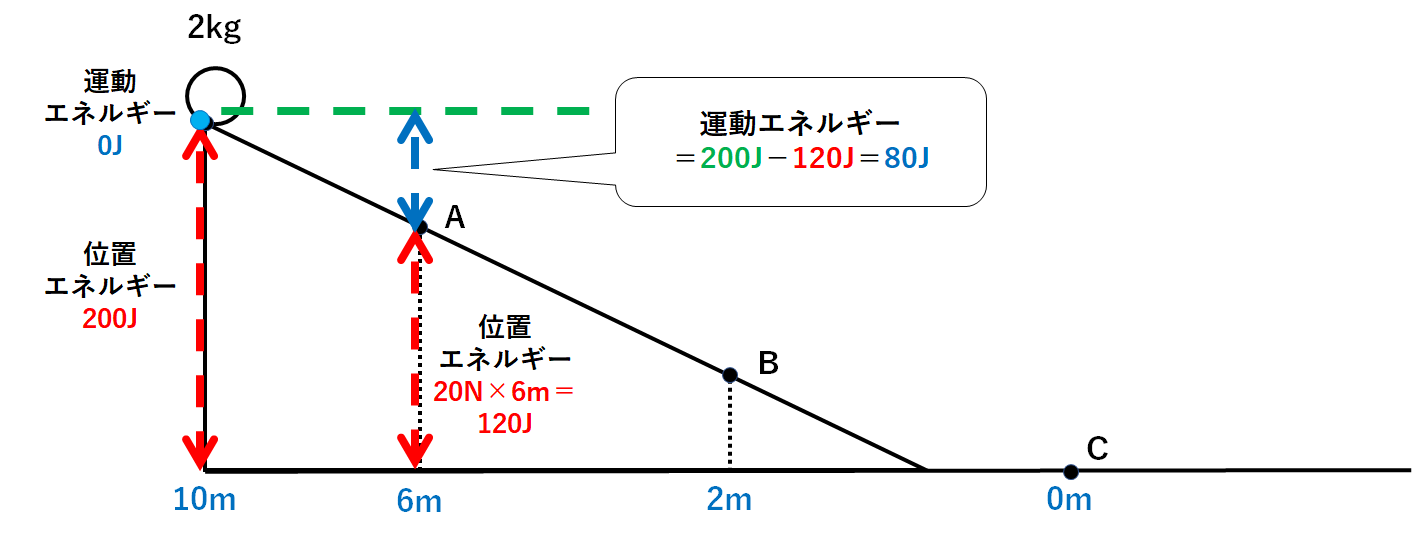
ここで、力学的エネルギーは200Jのまま保存されていました。

 

 

 

よって

運動エネルギー＝200J－120J＝80J

となります。(↓の図)

 

 

 

 

③B点を通過した瞬間

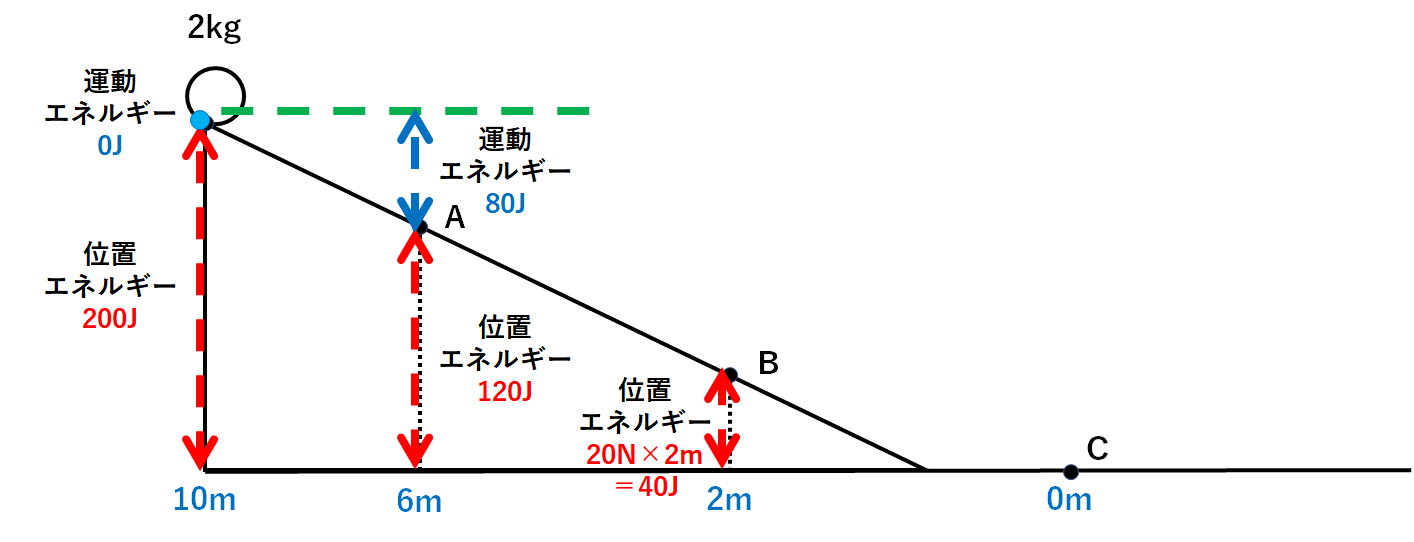
B点は高さ2mなので

B点での位置エネルギー＝20N×2m＝40J

です。(↓の図)

 

 

ここでも力学的エネルギーは200Jです。（力学的エネルギーの保存）

 

 

 

よって

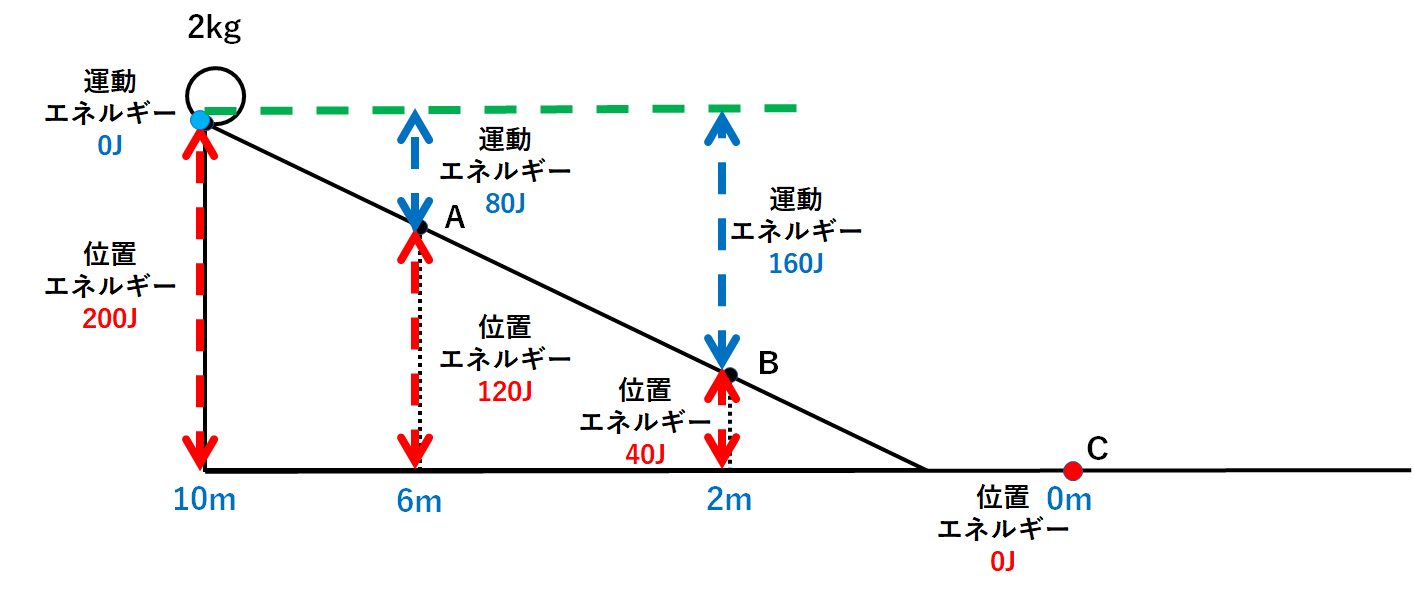
運動エネルギー＝200J－40J＝160J

となります。(↓の図)

 

 

A点通過時に比べると2倍の運動エネルギーを持っています。

つまりA点通過時より速さが大きいことがわかりますね。

 

④C点を通過した瞬間

C点は高さ0m。

よって

C点での位置エネルギー＝0J

です。

 

ここで力学的エネルギーは200Jです。(力学的エネルギーの保存)

 

ということは

運動エネルギー＝200J

となります。(↓の図)

つまりC点でもっとも運動エネルギーが大きい＝速さが大きいことになりますね。

 

このように力学的エネルギーが保存される場合は

運動エネルギーは、力学的エネルギーと位置エネルギーの差

として求めることができます。

 

また高さが低いところほど運動エネルギーが大きく、速さも大きいことになります。

 

グラフで見てみましょう。

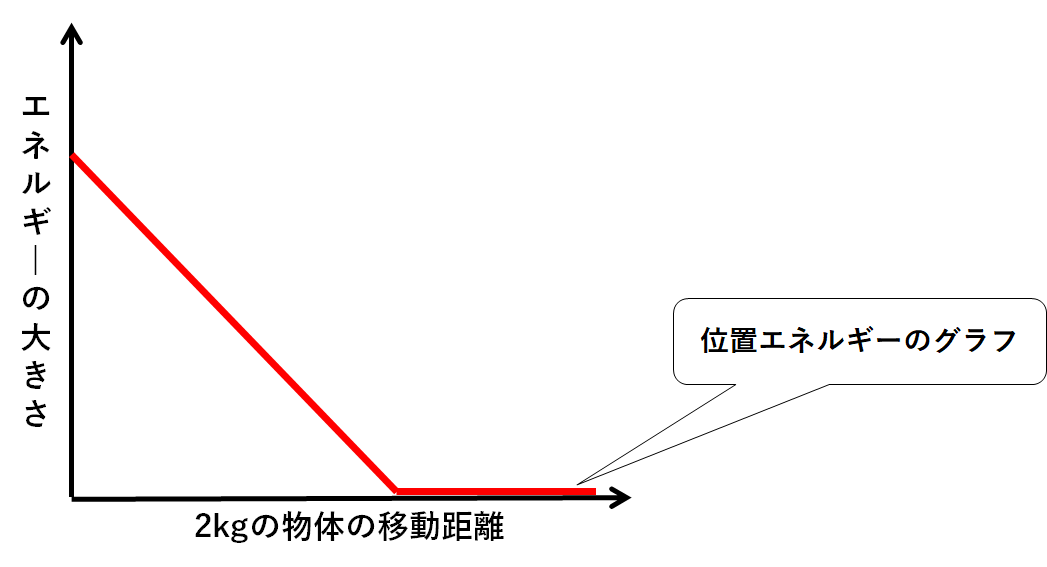
位置エネルギーは次のように変化していました。

 

一方で運動エネルギーは↓のようなグラフになります。

 

 

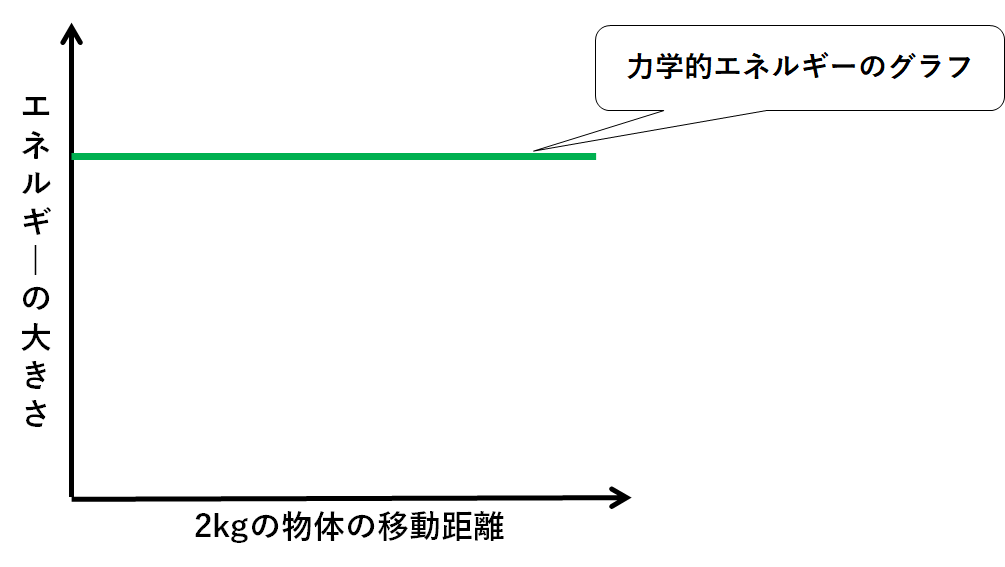
また力学的エネルギーは保存されているので↓のような一定のグラフになります。

 

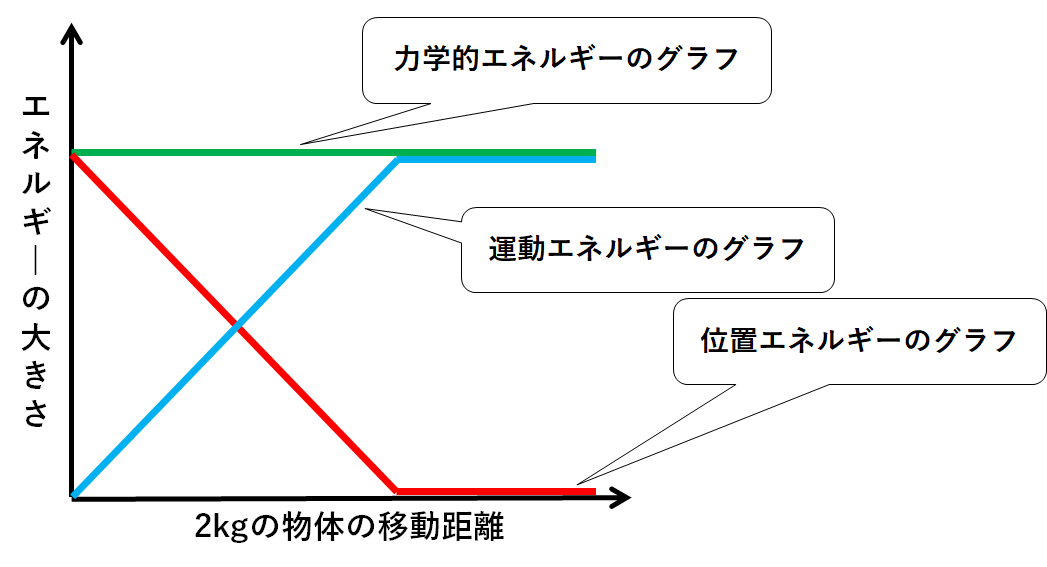
この3つを1つのグラフにまとめましょう。(↓の図)

 

このように力学的エネルギーが保存されるならば、

・低いところほど運動エネルギーは大きい(＝速い)

・位置エネルギーが増えると運動エネルギーは減る

・位置エネルギーが減ると運動エネルギーは増える

・つまり位置エネルギーと運動エネルギーは逆の変化をする

ということになります。