このページは浮力の求め方を解説しています。
アルキメデスの原理という考え方を使います。
中学校ではあまりやらないため、やや発展的ですが、それほど難しくありません。
高校物理でも知っておくとよい考え方です。
動画による解説は↓↓↓
※チャンネル登録は↓↓↓をクリック
より浮力の基本的な内容については→【浮力とは】←で解説しています。
1.アルキメデスの原理
浮力の大きさはその物体が押しのけた液体の重さに等しい。
※タイトルは暗記しなくていいので中身を覚えましょう。
浮力の大きさとして近年よく出題される求め方です。
とは言え、求め方はカンタン!
実際に次の例題を通して考えてみましょう。
例題1
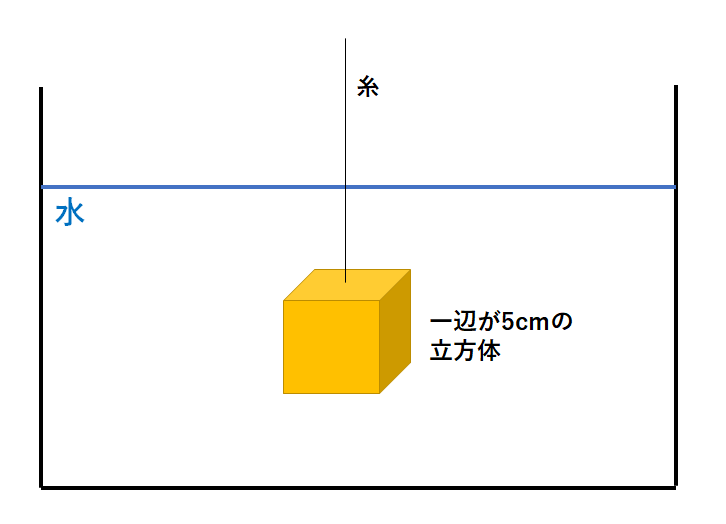
水の中に一辺が5cmの立方体を水中に沈めた。
このとき立方体にはたらく浮力は何Nか。
ただし100gの物体にはたらく重力を1Nとする。
(答)
この立方体の体積は
$$5cm×5cm×5cm=125cm^3$$
です。
この125cm3の立方体があるスペースには、もともと水があったはずです。
立方体は125cm3の水を押しのけたことになります。
浮力は「押しのけた液体の重さ」に等しいので
$$押しのけた液体の重さ=125cm^3の水の重さ$$
ということになります。
水の密度は1g/cm3なので
$$125cm^3の水の質量=125cm^3×1g/cm^3=125g$$
125gの水の重さは1.25N。
よって浮力は1.25Nとなります。
POINT!!
・浮力は、押しのけた液体の重さに等しい。
・沈んでいる部分の体積(cm3)を求める
→ 質量(g)に直す
→ 力(N)に直す
例題2
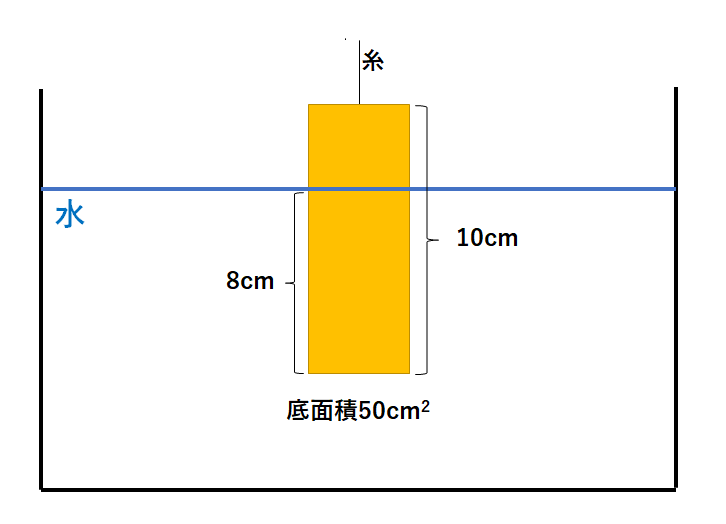
水の中に底面積が50cm2、高さが10cmの物体を水面から深さ8cmのところまで沈めた。
このとき物体にはたらく浮力は何Nか。
ただし100gの物体にはたらく重力を1Nとする。
(答)
この物体の水中に沈んでいる部分の体積は
$$底面積×高さ=50cm^2×8cm=400cm^3$$
です。
この400cm3の物体の部分にはもともと水があったので、物体は400cm3の水を押しのけたことになります。
水の密度は1g/cm3であるため
$$400cm^3の水の質量=400cm^3×1g/cm^3=400g$$
となります。
浮力の大きさは、押しのけた液体の重さに等しいので・・・
400gの水の重さは4Nであることから、浮力は4Nとなります。
例題3
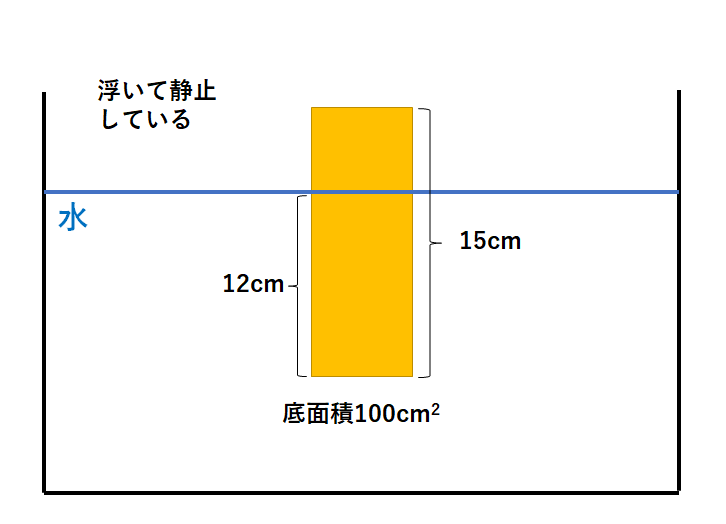
底面積100cm2、高さ15cmの物体が図のような状態で水に浮いて静止していた。
100gの物体にはたらく重力を1Nとして次の問いに答えよ。
(1)この物体にはたらく浮力は何Nか。
(2)この物体の質量は何gか。
(答)
(1)
この物体の水中に沈んでいる部分の体積は
$$100cm^2×12cm=1200cm^3$$
です。
つまり1200cm3の水を押しのけたことになります。
水の密度は1g/cm3であるため
$$1200cm^3の水の質量=1200g$$
押しのけた水の質量が1200gなので、その重さは12N。
よって浮力は12Nとなります。
(2)
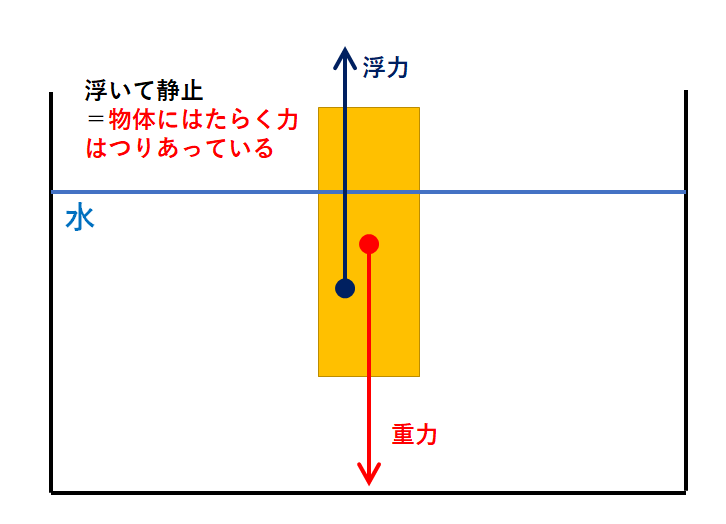
この物体には浮力以外にどんな力がはたらいているでしょうか。
もし浮力しかはたらいていないならば物体は水面から飛び出てしまうはず。
「静止している」ということは、浮力(上向き)とつりあっている下向きの力が存在することになります。
下向きの力・・・
それは重力以外にありません。(↓の図)
水に浮いて静止 → 浮力と重力がつりあっている、ということなんです。
よって物体の重力は浮力と同じ12N。
なので物体の質量は1200g(1.2kg)となります。
POINT!!
・物体が水に浮いて静止している・・・物体にはたらく浮力と重力がつりあっている!
こちらもどうぞ
浮力の計算問題を販売しています。
よければご覧ください。





コメント(承認された場合のみ表示されます)
[…] https://chuugakurika.com/2017/11/28/post-745/ […]