このページでは2018年度の奈良県立入試一般選抜の問題を解説しています。(理科のみ)
問題・模範解答はこちら↓↓↓↓
http://www.pref.nara.jp/17661.htm
大問1の解説
(1)
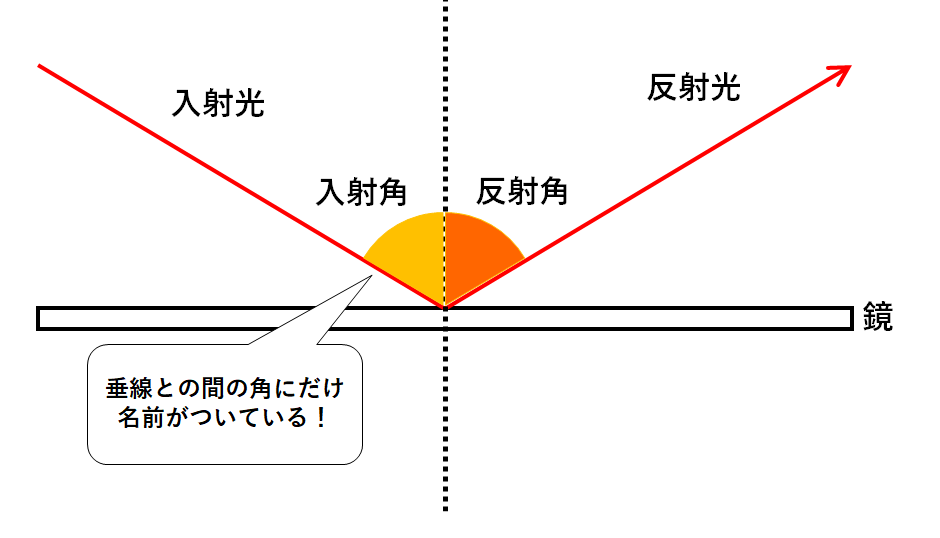
光の反射では、入射角と反射角が等しくなります。(↓の図)
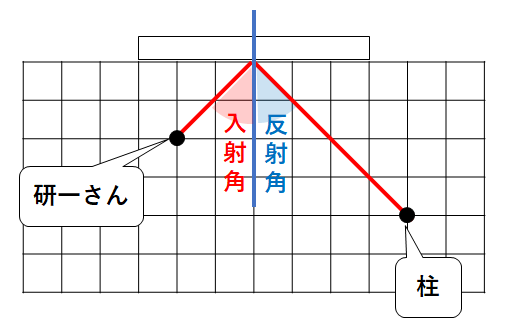
図2の場合、反射の様子は↓のようになります。(入射角=反射角となっている)
もし観測者がXの方向に動いたとしましょう。
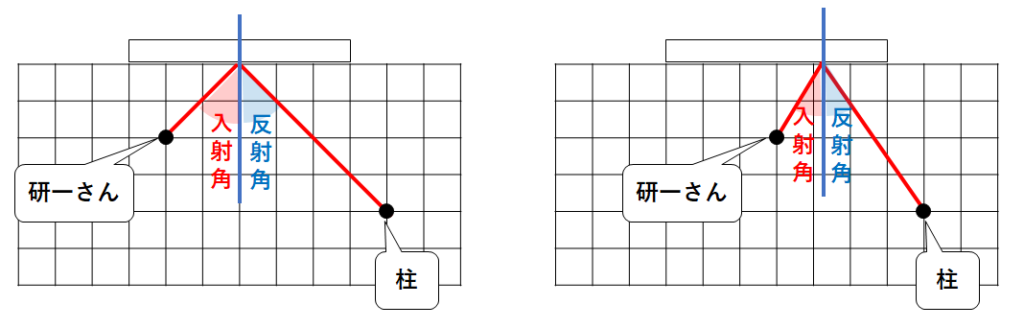
その場合の、光の反射の様子は↓のようになります。
元の場合よりも入射角・反射角ともに小さくなるのです。
そして、鏡に映る像は虚像と呼ばれます。
POINT!!
実像と虚像のちがい
・実像・・・光が集まってできる像
・虚像・・・光が集まっているわけではなく、そこにあるかのように見える像
※顕微鏡や望遠鏡、ルーペで見ているものは虚像。
(2)
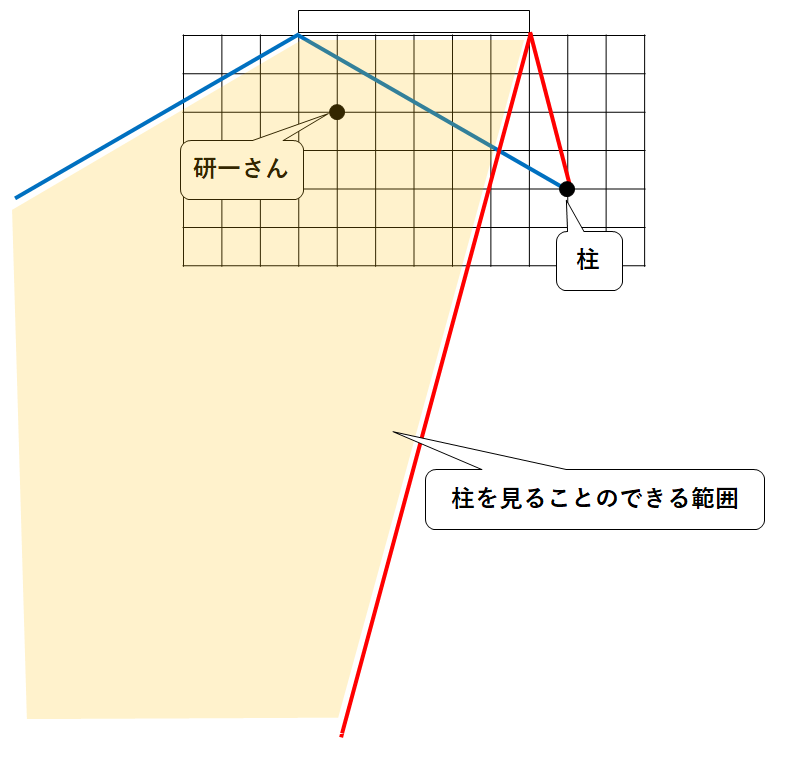
ガラスの面に映る柱が見える範囲を図2に表しましょう。
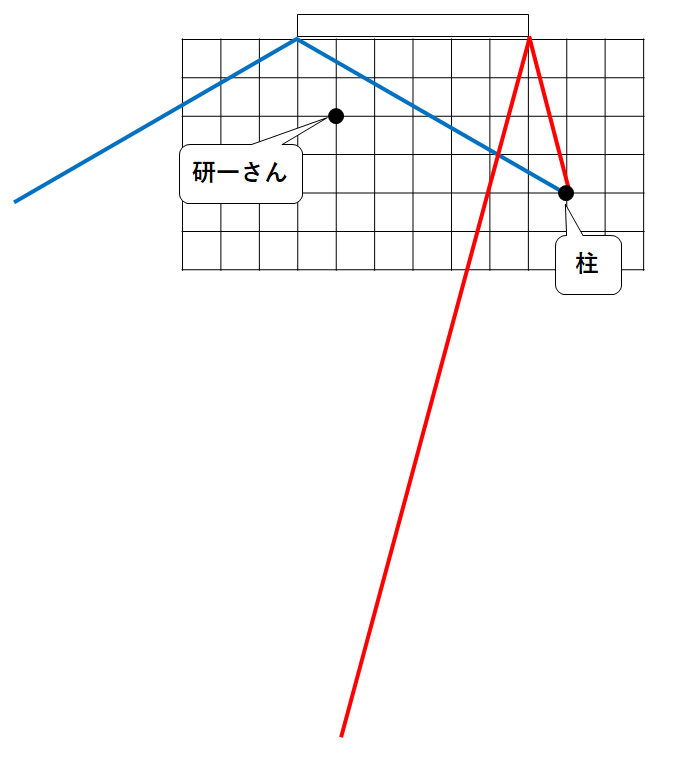
まず、柱から出た光が、鏡のふちにあたって反射する様子を書きます。(↓の図)
よって鏡に映った柱を見ることができるのは↓の色の付けた部分になります。
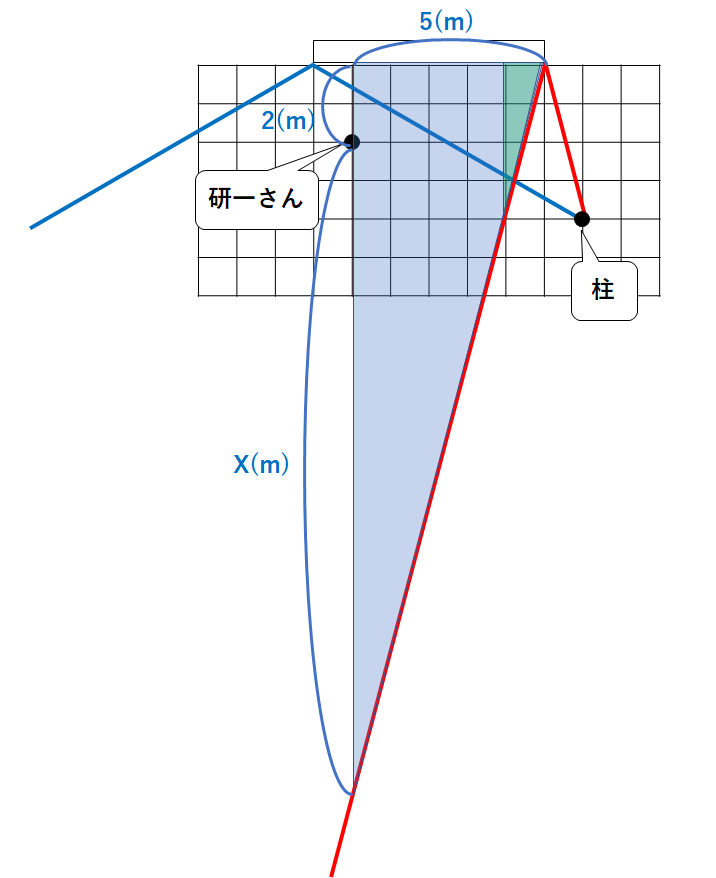
研一さんがY方向に動いて、柱が見えなくなるには↓の位置まで動かねばなりません。
この長さをx(m)としましょう。
そして三角形の相似の関係に注目。(青色の三角形 ∽ 緑色の三角形)
$$1:4=5:(x+2) $$
これを解いて
x=18
となります。
よってエが正解になります。
大問2の解説
(2)
問われているのは、金属の質量と化合した酸素の質量との関係です。
表に表されているのは、酸化物の質量であることに気を付けましょう。
例えば、表1。
A班では0.90gのマグネシウムを加熱しています。
その結果、酸化マグネシウムが1.50g生じています。
つまり化合した酸素は1.50-0.90=0.60gとなります。
このようにして酸素の質量を求めてグラフを書きましょう。
(3)
表1からもわかる通り、マグネシウムと酸素は3:2の質量比で化合します。
求める酸素の質量をx(g)とすると
$$3:2=0.45:x$$
これを解いて
x=0.30
となります。
よって答えは0.30gとなります。
(4)
H班では0.80gの銅を加熱しています。
そして1回目の加熱ののち、質量は0.97gとなっています。
1回目の加熱の段階で、すべての銅が酸化したわけでもなさそうです。
まず質量の増加から、反応した酸素の質量を求めましょう。
$$反応した酸素=0.97-0.80=0.17g$$
表2より、銅と酸素は4:1の質量比で化合します。
1回目の段階で反応した銅をy(g)とすると、
$$4:1=y:0.17$$
これを解いて
y=0.68
つまり0.80gの銅のうち、0.68gが反応したことがわかります。
よってその割合は
$$\frac{0.68}{0.80}×100=85%$$
となり、
85%の銅が酸素と化合したと求められます。
(5)
銅と酸素は4:1の質量比で反応します。
一方で
マグネシウムと酸素は3:2の質量比で反応します。
この問いでは、同じ質量の酸素と反応する銅とマグネシウムの質量を比べています。
もし酸素が2gあるとするとこれに反応する銅は8gです。
一方、2gの酸素の反応するマグネシウムは3gです。
よって同じ質量の酸素に反応する銅とマグネシウムの割合は
銅:マグネシウム=8:3
となります。
求める答えは
$$8÷3=2.666・・・≒2.7$$
2.7倍となります。
大問3の解説
(1)
地球型惑星・・・岩石を主成分とし、密度が高い。水星・金星・地球・火星。
木星型惑星・・・ガスを主成分とし、密度が低い。木星・土星・天王星・海王星。
(2)①
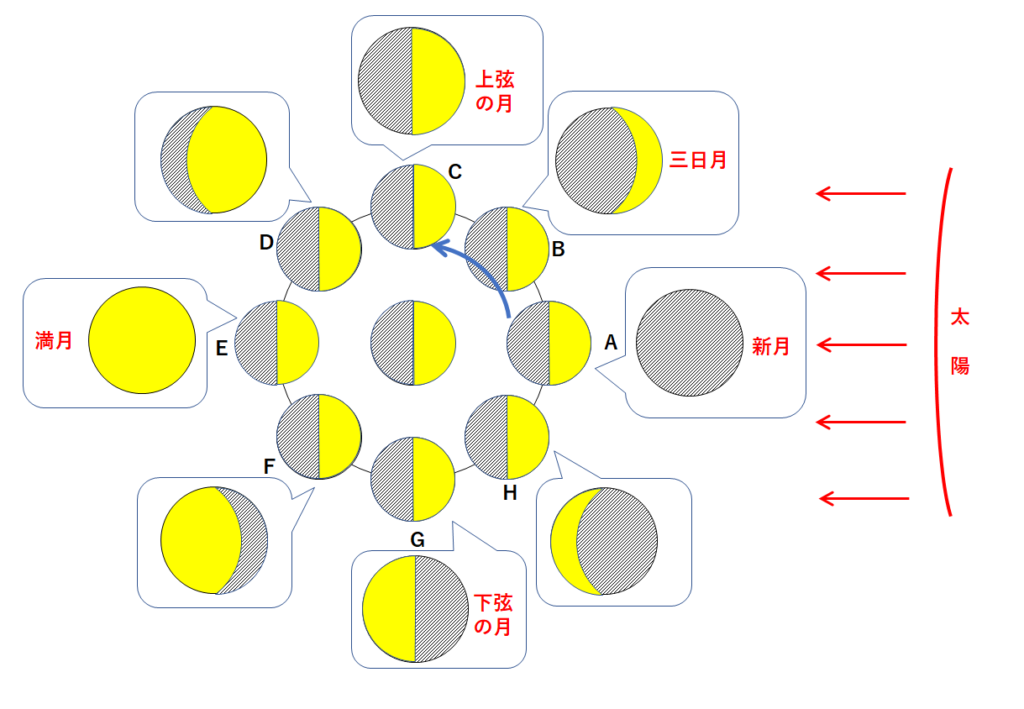
月の満ち欠けは↓のように変化します。
図1では三日月が見えているため、光る部分の大きさは大きくなります。
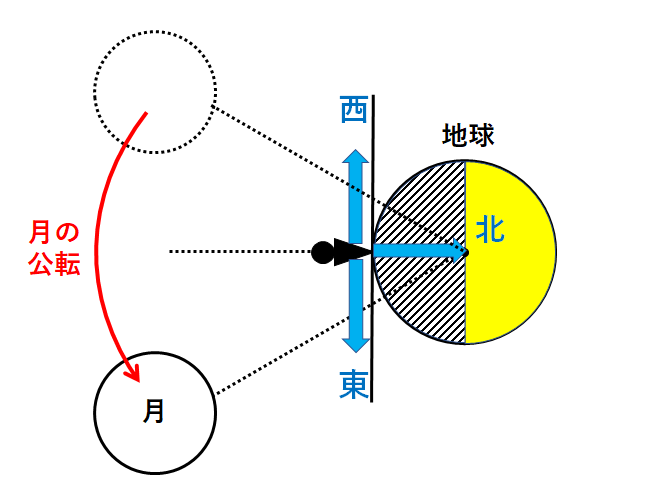
この間、月は↓のように公転をしていきます。
よって月は西の空から東の空へと移り変わっていきます。
(2)②
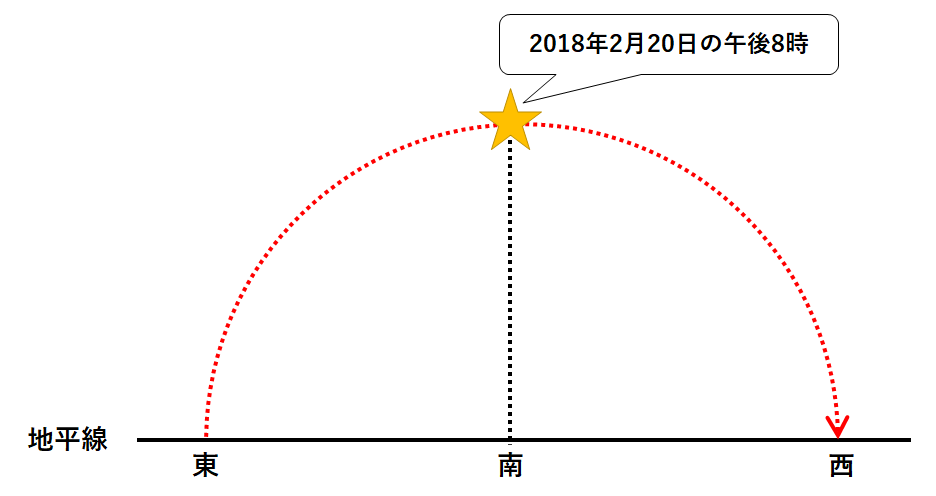
図1と問題文から、
オリオン座は
2018年2月20日の午後8時に南中
していることがわかります。(↓の図)
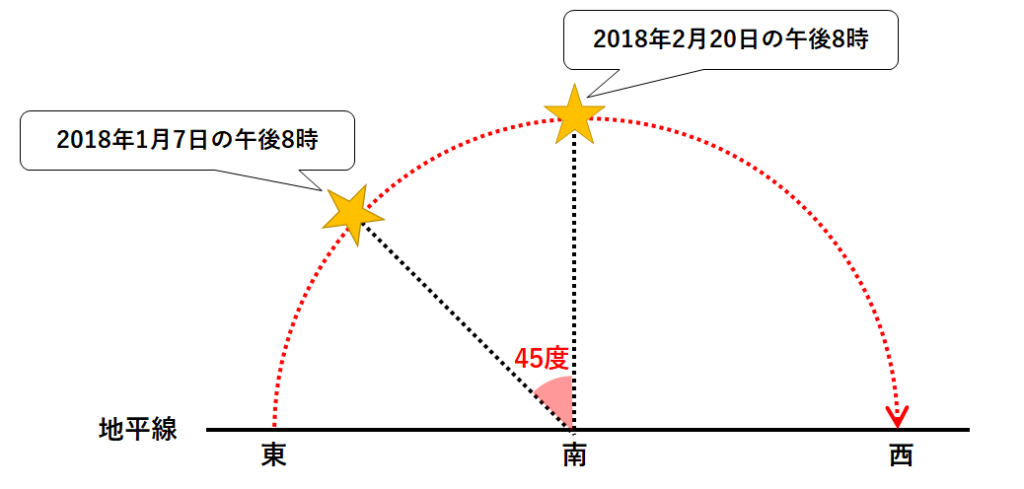
この問いの2018年1月7日(約1.5か月前)を考えましょう。
まず2017年1月7日の午後8時。
星の年周運動を考えると、↓のような位置にオリオン座があります。
POINT!!
・星の年周運動
星座をつくる星の位置は、1ヶ月で30度ずつずれる。
→この問いでは約1.5か月前なので、45度のずれ。
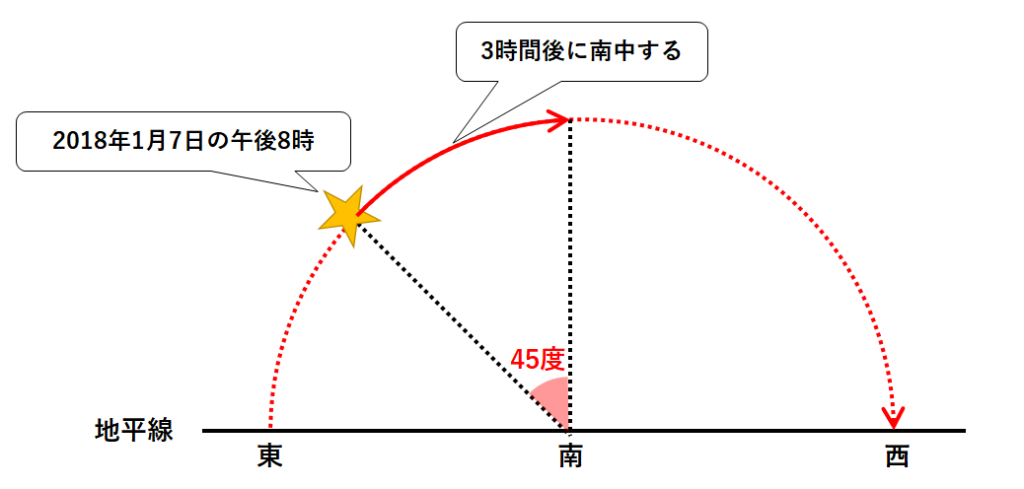
このオリオン座は、この数時間後に南中すると考えられます。
星の日周運動を考えると、南中までに3時間かかると考えられます。(↓の図)
POINT!!
・星の日周運動
星座をつくる星の位置は、1時間で15度ずつずれる。
→この問いでは45度のずれなので、3時間かかる。
よって2018年1月7日の午後11時ごろに南中すると考えられます。
(3)
イとエが誤りです。
イの選択肢では・・・
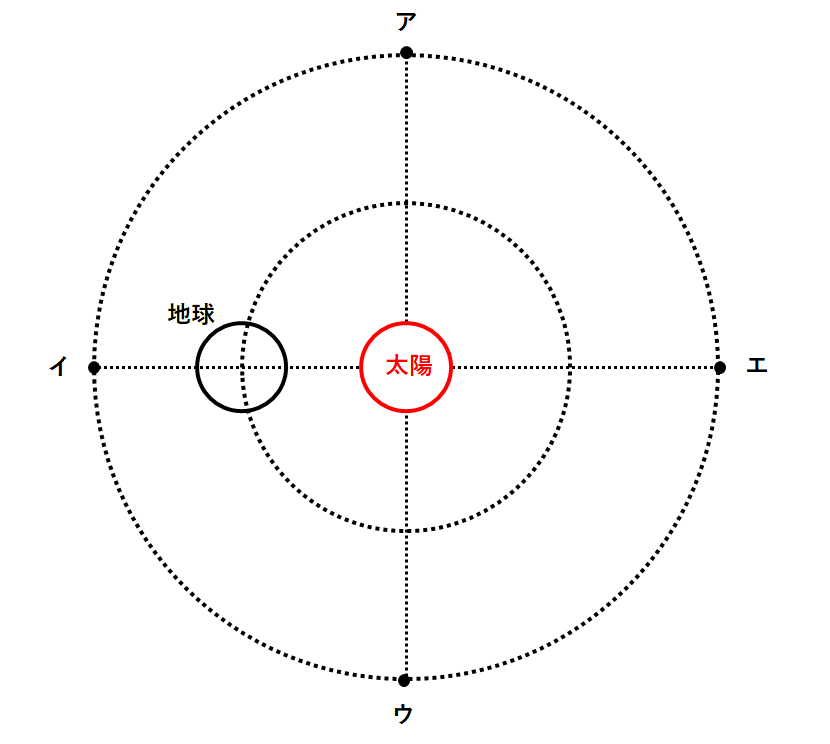
月と金星が同時に西の空に見えるときを考えています。
金星が西の空に見えるのは、夕方ごろ。
POINT!!
金星の見え方は次の2通りしかない。
・明け方、東の空に見える(明けの明星)。
・夕方、西の空に見える(よいの明星)。
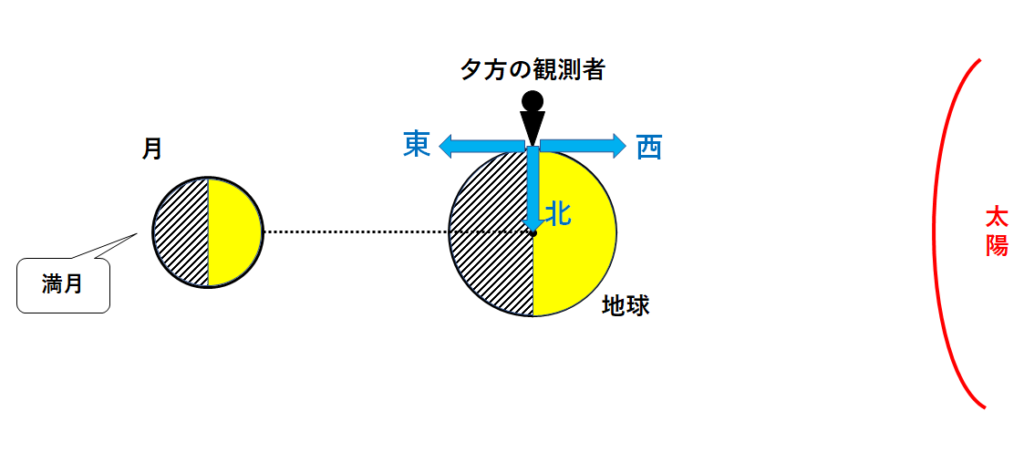
↓の図は、太陽と地球、満月の位置関係を表しています。
夕方の観測者から見て、満月は東の空にあります。
よってイの選択肢は誤りとなります。
エの選択肢では・・・
星座の星が、月よりも地球に近い位置に見えるか?
ということが問われています。
星座の星は非常に遠い位置にあるため、月よりも手前に見えることはありません。
よってエの選択肢も誤りとなります。
(4)
図2を↓のように書き直します。
まず
皆既月食・・・月の位置が満月の位置
皆既月食が沈む・・・月は西の空に沈む
ということです。
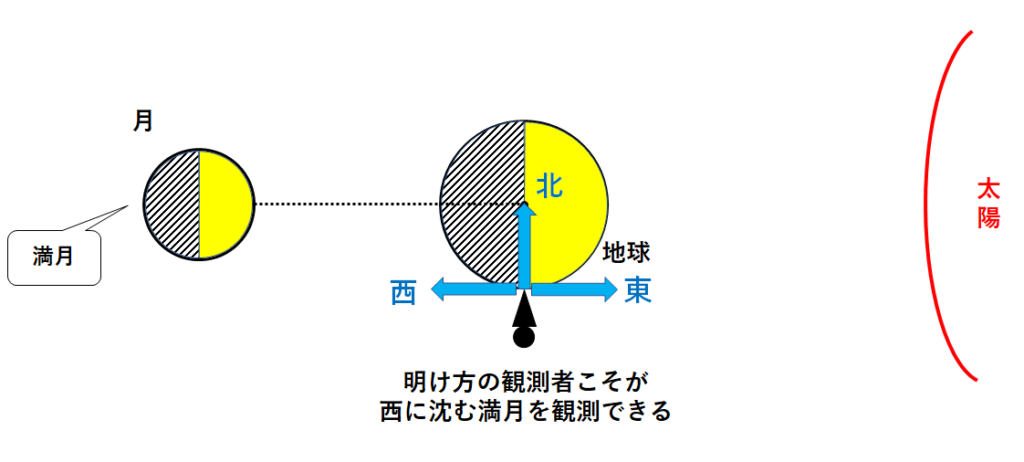
つまり、この問いでは満月が西の空に見えるころの話をしています。
満月が西の空に見えるのは明け方です。(↓の図)
このときに「オリオン座が東の空からのぼってくる」とあります。
オリオン座は明け方、東の空に見える
ということです。
明け方の観測者から見て、東の空はエの星座が見えるはず。
よってエがオリオン座の位置ということになります。
大問4の解説
(1)
大前提として、水蒸気は目に見えません。
例えば、湯気や雲は目に見えます。
つまり湯気や雲の正体は、水蒸気ではないのです。(正体は細かな水滴)
ア「容器の表面がくもる」、イ「霧」、ウ「はく息が白くなる」
はすべて目に見えますよね。
これらの正体はすべて水滴です。
よってエのみが正解となります。
(2)
条件を整理しましょう。
加湿器を作動させる前は
気温22度・湿度45%・部屋の大きさ100m3
↓
加湿器を作動させた後は
気温22度・湿度60%・部屋の大きさ100m3
となります。
加湿器を作動させる前について、部屋全体含まれる水蒸気の量は
$$19.4×\frac{45}{100}=8.73g/m^3$$
$$8.73g/m^3×100m^3=873g$$
加湿器を作動させた後について、部屋全体含まれる水蒸気の量は
$$19.4×\frac{60}{100}=11.64g/m^3$$
$$11.64g/m^3×100m^3=1164g$$
よって水蒸気をどれだけ増やすべきかというと
$$1164g-873g=291g$$
となります。
したがって加湿器で291gの水蒸気を放出する必要があることになります。
大問5の解説
(1)①
対物レンズは、高倍率のものほど長いです。
(ちなみに接眼レンズは、低倍率のものほど長い)
よって対物レンズからプレパラートまでの距離は短くなります。
(1)②
顕微鏡の倍率=接眼レンズの倍率×対物レンズの倍率
で求められます。
よってこの問いの場合、
$$10倍×40倍=400倍$$
となります。
(2)
三日月形の細胞を孔辺細胞といい、すきまの部分(X)を気孔といいます。
気孔では、
・光合成や呼吸による酸素と二酸化炭素の出入り
・蒸散による水蒸気の放出
が行われています。
(4)
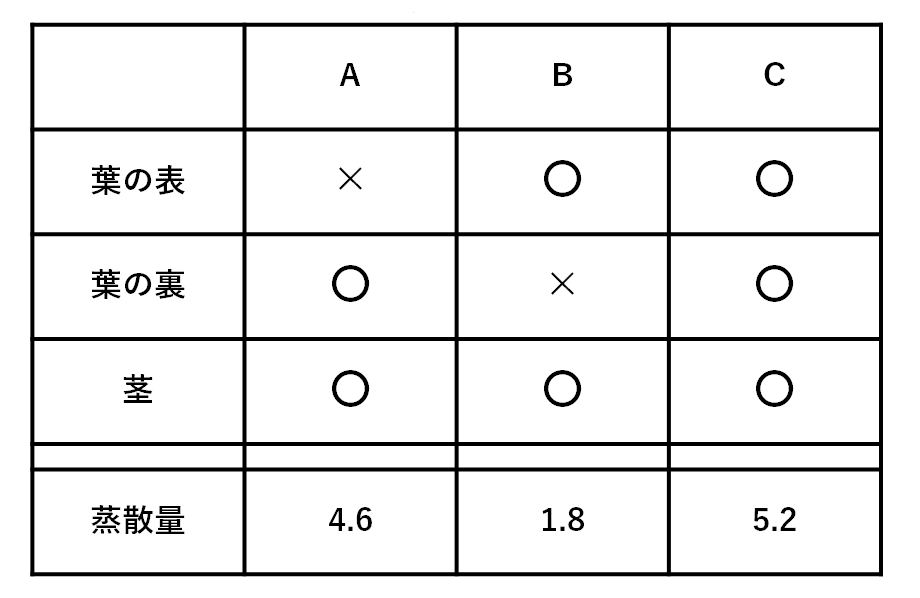
表1、表2の結果をまとめてみます。
〇の箇所は「蒸散をした」という意味です。
よって枝Aと枝Bの水の減少量ちがいは、
葉の裏からの蒸散量と葉の表からの蒸散量のちがいを意味していることとなります。
したがって
葉の裏からの蒸散量は、葉の表からの蒸散量より多い
ということがわかります。
(5)
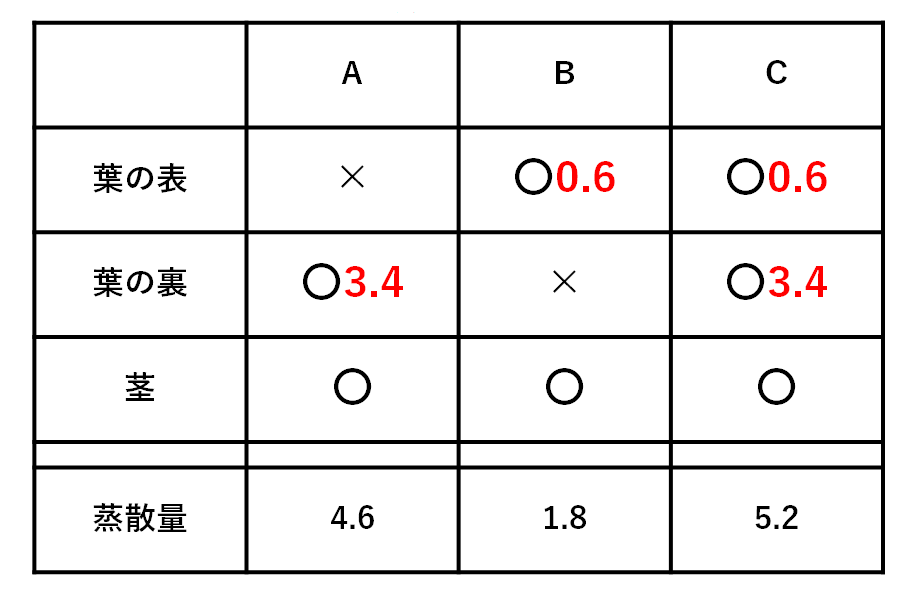
先ほどの表を用いて考えます。
AとCの比較から
葉の表からの蒸散量=5.2-4.6=0.6
とわかります。
またBとCの比較から
葉の裏からの蒸散量=5.2-1.8=3.4
とわかります。
よって葉以外の部分(茎)での蒸散量は
Aに注目して
茎からの蒸散量=4.6-3.4=1.2
となります。
大問6の解説
(1)
力とは、物体どうしが接しているところにはたらきます。
(物体どうしの接しているところには必ず作用点がある)
接していなくてもはたらく力は
重力・磁力・静電気力
です。
この問いでは、重力とつりあう力を考えています。
この力の作用点は、物体と床の接しているところ。
その力の向きは、重力とは反対向き。
よってアとなります。
(2)
仕事は次のように求めます。
$$仕事(J)=力(N)×力の向きに動いた距離(m)$$
よって表の②の部分より
$$2.0N×0.4m=0.8J$$
となります。
(3)
(2)と同じように、方法①と方法③の仕事を求めましょう。
方法①は
$$4.0N×0.2m=0.8J$$
方法③は
$$2.5N×0.32m=0.8J$$
※本当は計算せずとも、
図1~図3すべてで同じ物体を20cmの高さまで上昇させていることから、仕事の量も同じと判断しましょう。(仕事の原理)
そして仕事率を求めてみましょう。
$$仕事率(W)=\frac{仕事(J)}{時間(s)}$$
方法①は
$$\frac{0.8J}{4s}=0.2W$$
方法②では
$$\frac{0.8J}{8s}=0.1W$$
方法③では
$$\frac{0.8J}{5s}=0.16W$$
よって
方法①→方法③→方法②
という順になります。



コメント(承認された場合のみ表示されます)