このページでは「圧力って何?」「圧力の求め方・計算方法」について解説しています。
※指導要領の改訂により、2020年以降に中1になった人は中2でこの単元を学習します。(今までは中1で習っていました)
動画による解説は↓↓↓
チャンネル登録はこちらから↓↓↓
1.圧力とは
単位面積あたりにはたらく力。
多くの場合、1m2あたりにはたらく力のこと。
このときの単位は【N/m2】(ニュートン毎平方メートル)と書く。
ほかにも【Pa】(パスカル)や【hPa】(ヘクトパスカル)という単位もある。
1N/m2=1Pa
1hPa=100Pa=100N/m2
※むかし質量100gの物体にはたらく重力は「100g重」と表していました。1hPa=1g重/cm2の関係があります。
圧力の意味をきちんと理解しておきましょう。
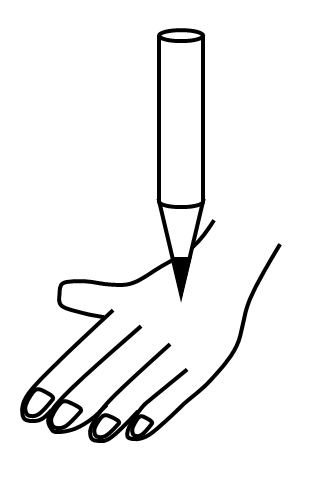
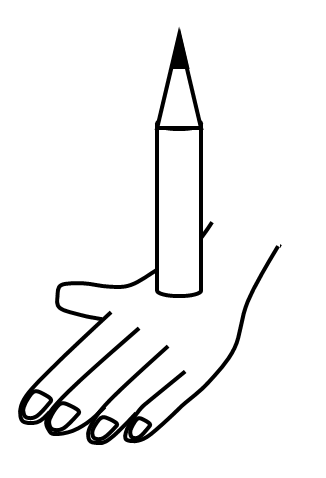
次の①②のように手に鉛筆をのせてみます。
これで圧力をイメージしてみましょう。
①、②のどちらの方が痛いでしょう。
もちろん①の方ですよね。
でもどちらも同じ鉛筆をのせているわけですから、手には同じ重さ(鉛筆の)が加わっています。
手には同じ力が加わっているのになぜ①の方が痛いのでしょうか?
①は「とがっている面」が手に接しているからですよね。
言い換えてみます。
とがっている=手に接している面積が小さいということです。
つまり同じ力を受けたとしてもその力を受ける面の面積によって痛みは変わるということです。
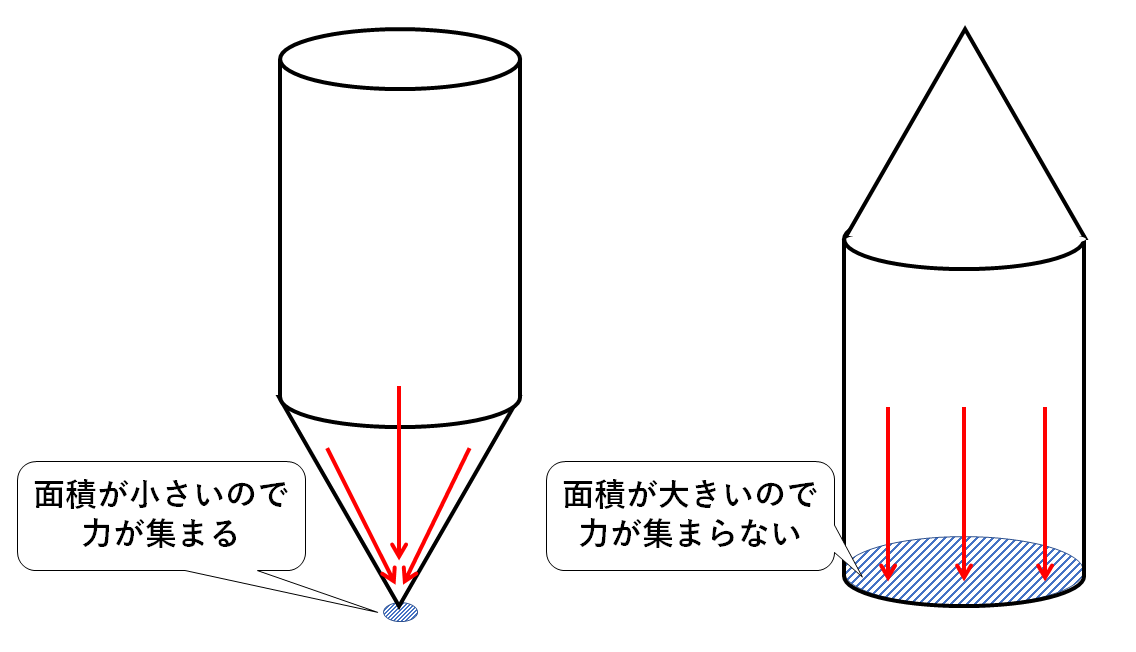
↓の図のように小さな面の方が力は集まり、大きな面では力は散らばってしまう。
このような力の集まり具合のことを圧力というのです。
・圧力が大きい…ある一定の面積にたくさんの力が集まっている。
・圧力が小さい…ある一定の面積に力が散らばってしまっている。
「一定の面積」というのを多くの場合1m2あたりで考えます。(問題によっては1cm2あたりを考えることもあります)
圧力の求め方は次のようになります。
$$圧力(N/m^2)=力(N)÷面積(m^2)$$
※単位の関係
1kg → 10N(100g → 1N)
1m2=10000cm2
では次の例題で圧力の計算の仕方を見ていきます。
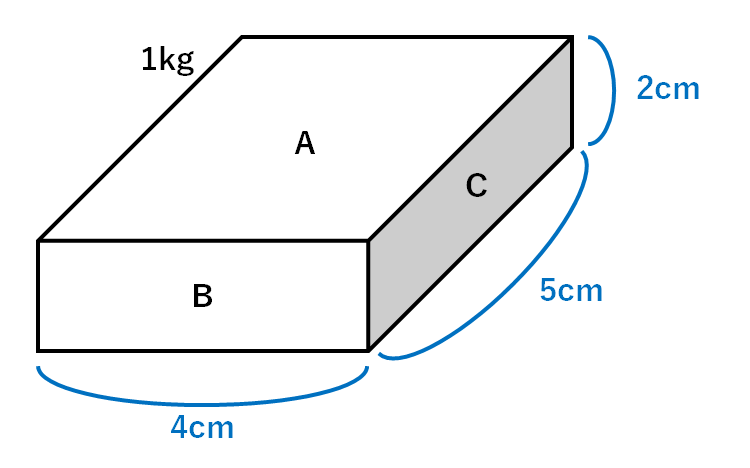
【例題1】
(答)
次の①~③のように求めていきます。
①Aの面を下にした場合の圧力
条件を整理しましょう。
・床にはたらく力=重さに等しいので1kg → 10N
・Aの面の面積=4cm×5cm=20cm2
多くの場合、圧力は「m2」で考えなければなりません。
つまり20「cm2」の単位ではだめでを「m2」になおす必要があるのです。
▼小数に直すなら…
10000cm2=1 m2 なので 20cm2=0.002m2 とできます。
▼分数に直すなら…
cm2からm2に直すには数字を1/10000倍します。
(例えば… 850000cm2=850000×1/10000=85m2)
よって
$$20cm^2=\frac{20}{10000}m^2$$
とできます。
※分数に直すやり方の方がおすすめです。ややこしい小数の計算をする必要がなく計算ミスを起こしにくいためです。
以下は分数に直したとして計算します。
・床にはたらく圧力
$$圧力=力÷面積=10N÷\frac{20}{10000}m^2$$
$$=10N×\frac{10000}{20}=5000N/m^2$$
よって圧力は5000N/m2となります。
ちなみに5000N/m2=5000Pa=50hPaとも書けますね。
②Bの面を下にした場合の圧力
・床にはたらく力=重さに等しいので 1kg → 10N
・Bの面の面積=4cm×2cm=8cm2
これを(m2)になおすと
$$8cm^2=\frac{8}{10000}m^2$$
・床にはたらく圧力
$$圧力=力÷面積=10N÷\frac{8}{10000}m^2$$
$$=10N×\frac{10000}{8}=12500N/m^2$$
これで12500N/m2とわかりました。
ちなみに12500N/m2=12500Pa=125hPaとも書けます。
③Cの面を下にした場合の圧力
・床にはたらく力=重さに等しいので 1kg → 10N
・Cの面の面積=5cm×2cm=10cm2
これを(m2)になおすと
$$10cm^2=\frac{10}{10000}m^2$$
・床にはたらく圧力
$$圧力=力÷面積=10N÷\frac{10}{10000}m^2$$
$$=10N×\frac{10000}{10}=10000N/m^2$$
これで10000N/m2とわかりました。
ちなみに10000N/m2=10000Pa=100hPaとも書けます。
3.圧力と面積
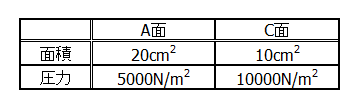
先ほどの例題1の計算結果を表にまとめてみます。
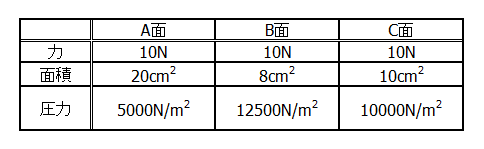
ここからわかるのは…
①力はどの面を下にしても変わらない。
②圧力は面積が小さいほど大きい。
→ 例)くぎやフォークなど・・・先端がとがっている
→ 面積を小さくすることで圧力を大きくして刺しやすくしている
③圧力は面積が大きいほど小さい。
→ 例) スキーの板・・・圧力を小さくして雪に沈みにくくしている
面積が10cm2→20cm2と2倍に変化すると
圧力は10000N/m2→5000N/m2と1/2倍に変化しています。
つまり面積と圧力は反比例の関係にあるということです。
4.圧力から力を求める
圧力の求め方である
$$圧力(N/m^2)=力(N)÷面積(m^2)$$
この式を変形すると
$$力(N)=圧力(N/m^2)×面積(m^2)$$
となります。
余裕がある人はこちらも使いこなせるようにしましょう。
【例題2】
(答)
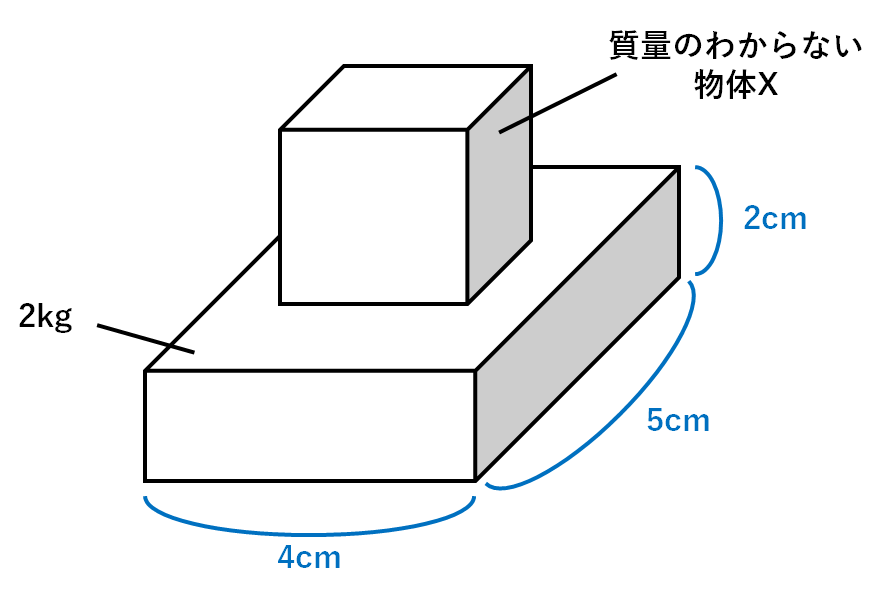
一般的に多い解法は物体Xの重さをx(N)として方程式をつくる解き方でしょうか。
ここでは違う解き方をしてみましょう。
$$力(N)=圧力(N/m^2)×面積(m^2)$$
を用いて床にはたらく力が何Nかを求めます。
・圧力・・・15000N/m2
・面積・・・4cm×5cm=20cm2
これをm2に直すと
$$20cm^2=\frac{20}{10000}m^2$$
よって
$$力[N]=圧力[N/m^2]×面積[m^2]=15000N/m^2×\frac{20}{10000}m^2$$
$$力[N]=30N$$
となりますね。
このうち直方体の重さは20Nなので
$$物体Xの重さ[N]=30N-20N=10N$$
つまり物体Xの質量は
10N → 1kg となるわけです。
※これ以外にも水圧や大気圧の問題で 力(N)=圧力(N/m2)×面積(m2)の式 をよく用います。
中3段階では必ず習得しておきたい式です。
・圧力(N/m2)=力(N)÷面積(m2)は必ず覚える
・単位変換に注意。特にcm2をm2に直すには数字を1/10000倍する。
・できれば力(N)=圧力(N/m2)×面積(m2)も覚える。
こちらもどうぞ
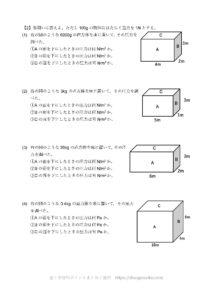
このページの例題のような問題を集めた圧力の計算ドリルを販売中です。
PDF形式のダウンロード販売です。
1つ220円(税込)です。


コメント(承認された場合のみ表示されます)
[…] ※圧力については→【圧力】←を参考に。 […]