中2化学【気体の発生に関する計算】

このページでは

「金属と塩酸が反応して水素が発生する」

「石灰石と塩酸が反応して二酸化炭素が発生する」

などの気体が発生する実験に関する計算問題について解説しています。

また過不足のある計算についても取り扱います。

動画による解説は↓↓↓

チャンネル登録はこちらから↓↓↓

※化学変化の基本的な計算手法については　→【定比例の法則(酸化)】←　を参考に。

1．気体の発生と定比例の法則

次のような実験を考えてみます。

実験

うすい塩酸800mLが入ったビーカーを用意します。

そこにさまざまな質量のマグネシウムリボンを加えてみます。

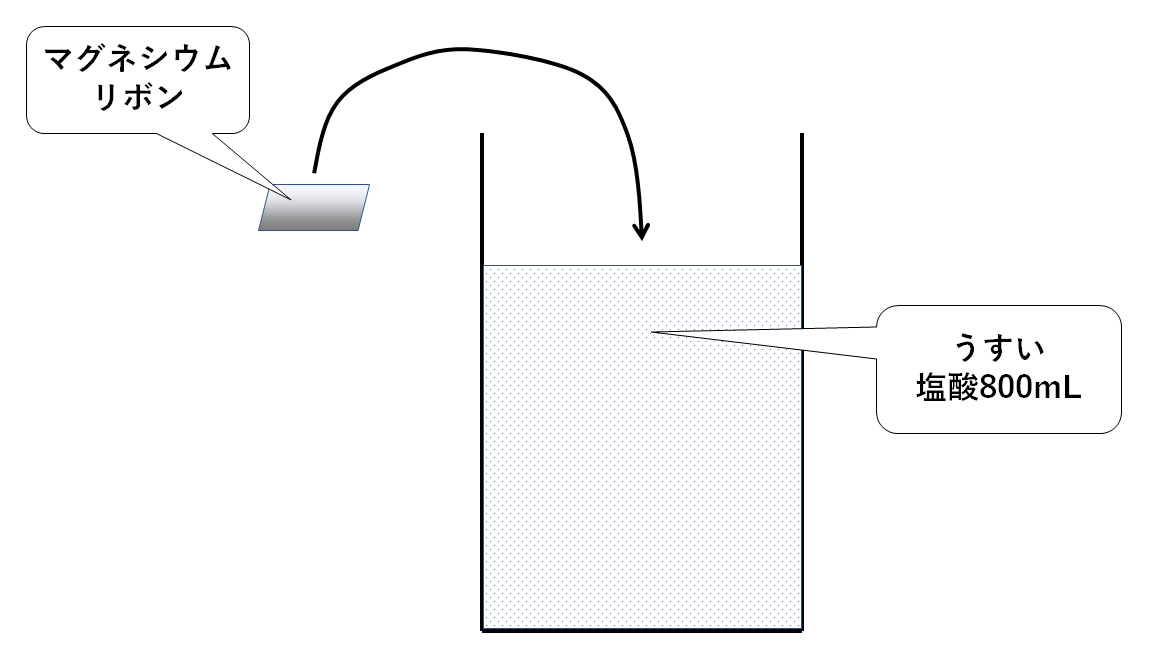
そのとき発生した水素を水上置換法でもれなく集め、体積を測定します。

いま

うすい塩酸800mLとマグネシウムリボン0.1gのとき

うすい塩酸800mLとマグネシウムリボン0.2gのとき

うすい塩酸800mLとマグネシウムリボン0.3gのとき

・
・
・

うすい塩酸800mLとマグネシウムリボン0.6gのとき

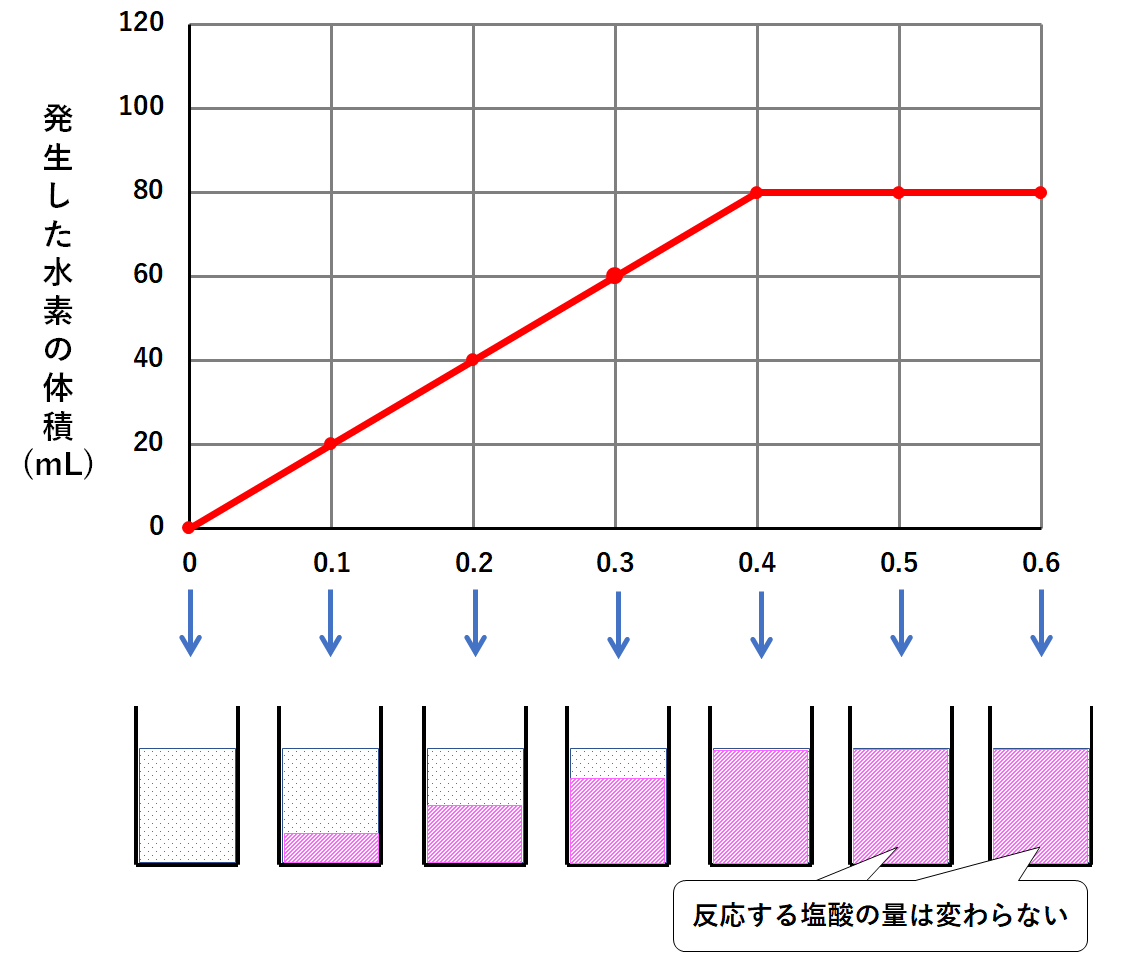
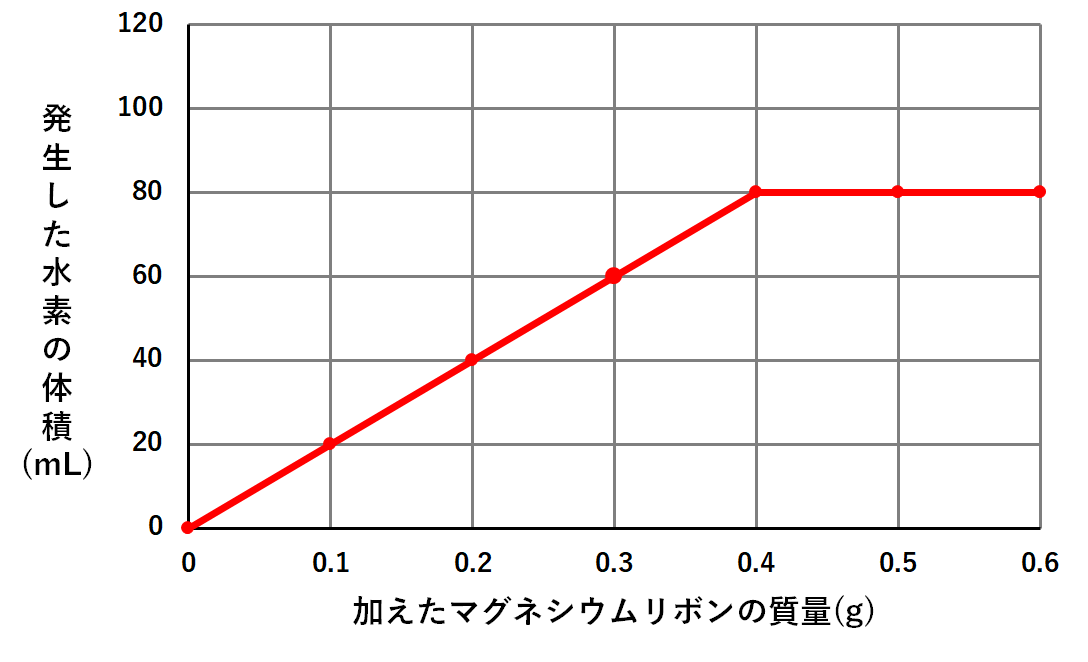
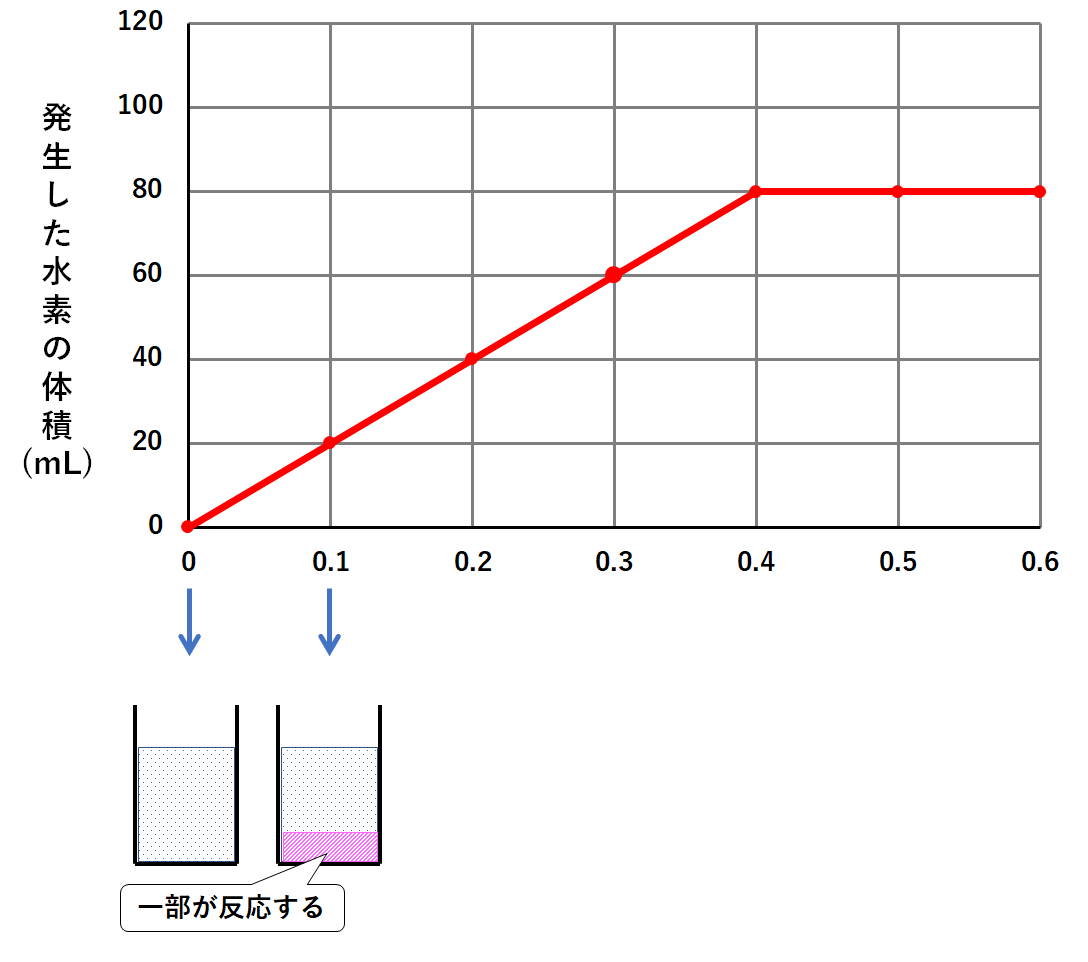
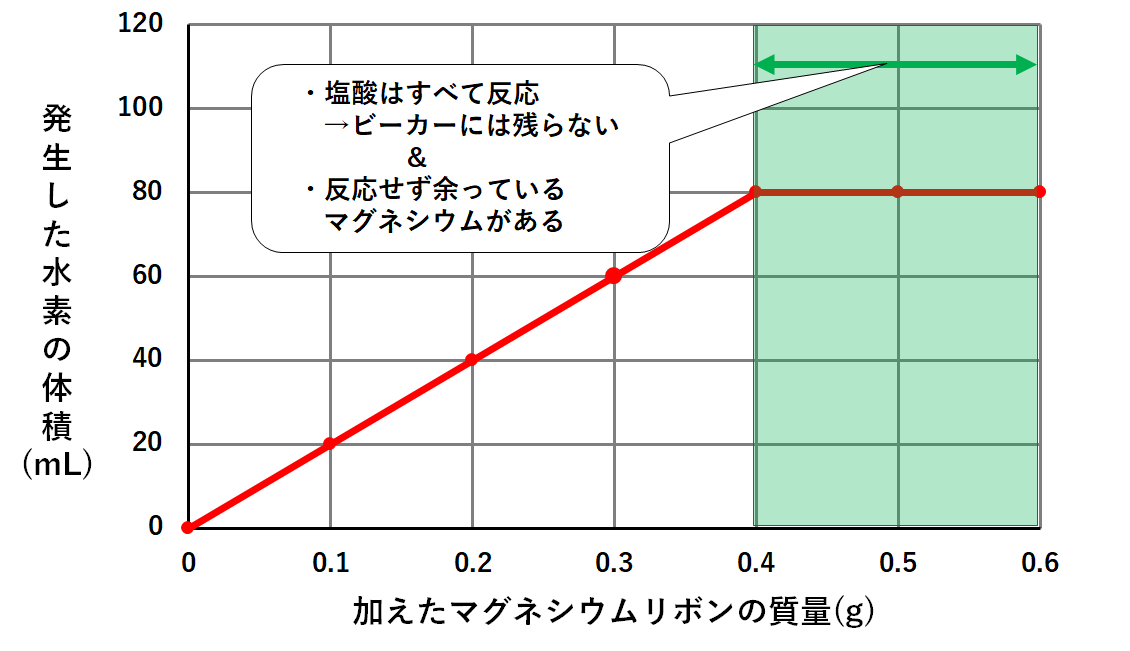
このそれぞれの場合で発生した水素の体積を調べると次のようなグラフになりました。

このグラフの意味を考えてみましょう。

①グラフの形の意味すること

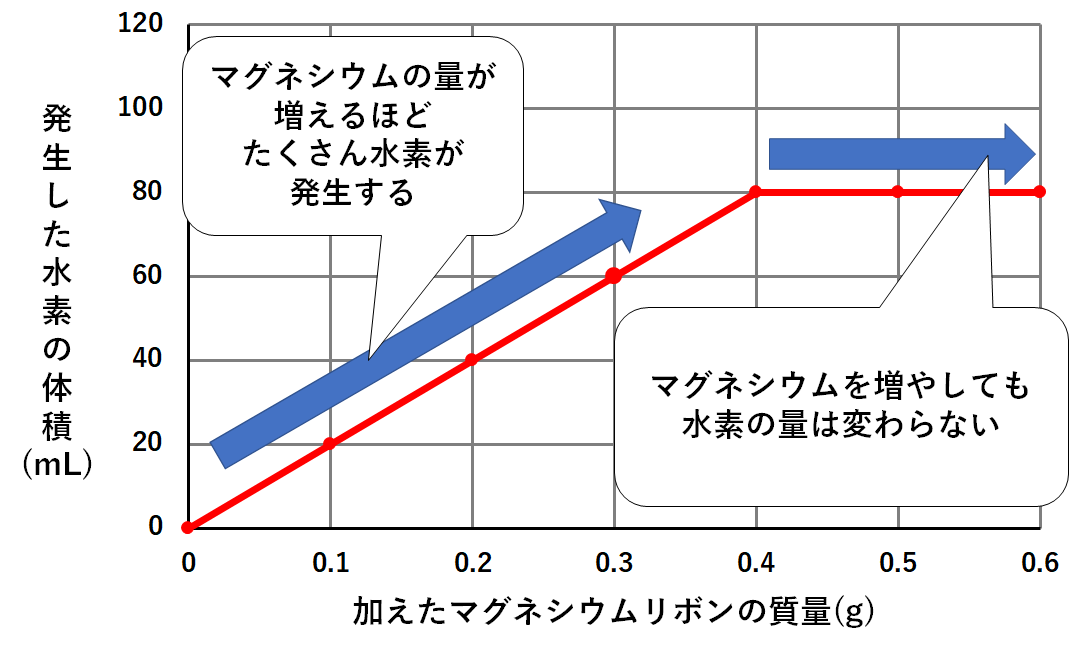
単純に考えれば

マグネシウムが増えれば増えるほど、発生する水素も増える

はずです。

確かにグラフはマグネシウム0.4gのところまでは発生する水素も増えています。

しかしマグネシウムをそれ以上加えても、発生する水素は増えないのです。(↓の図)

②グラフの意味をもっと考えてみよう

マグネシウム0.1gを加えたときというのは、塩酸が少しだけ反応します。(↓の図)

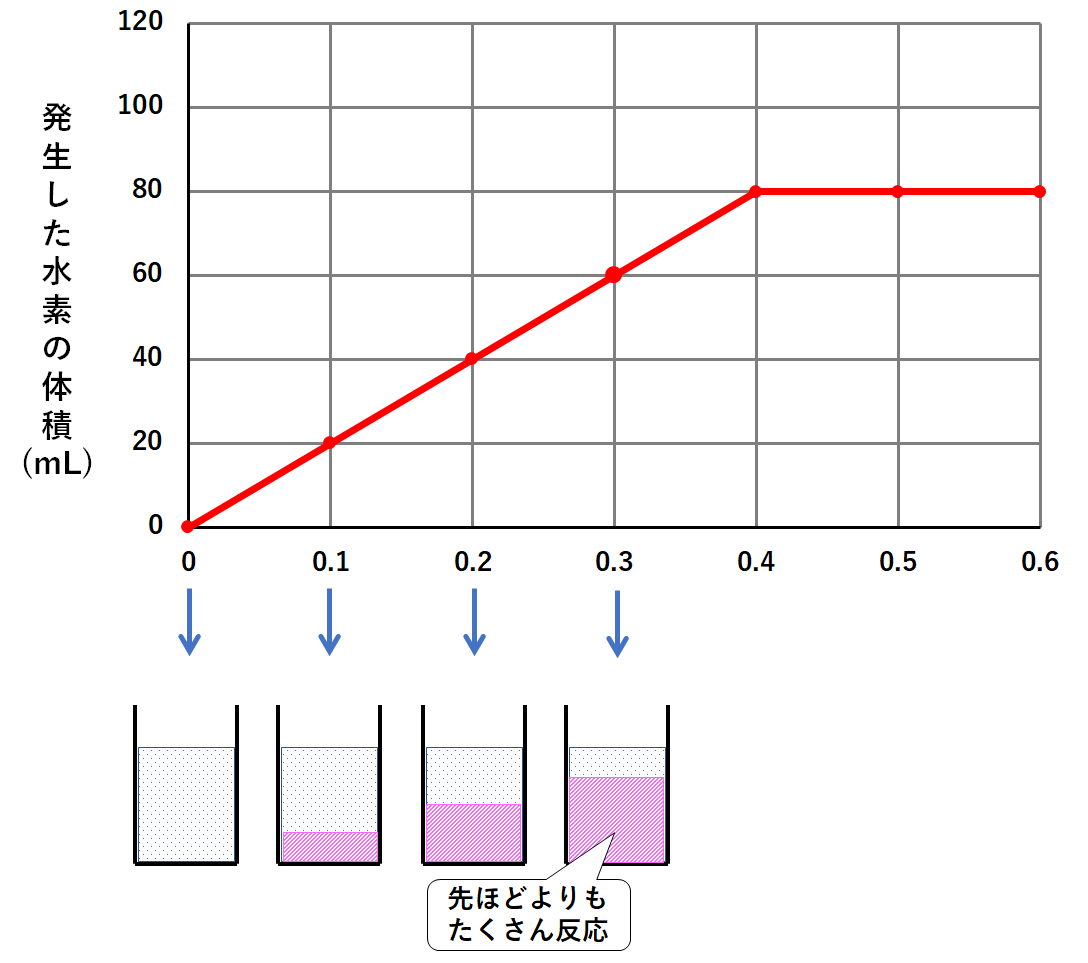
マグネシウム0.2gを加えたとき、塩酸が先ほどよりも多く反応します。(↓の図)

マグネシウム0.3gを加えたとき、塩酸がより多く反応します。(↓の図)

マグネシウム0.4gを加えたとき、塩酸がさらに多く反応します。(↓の図)

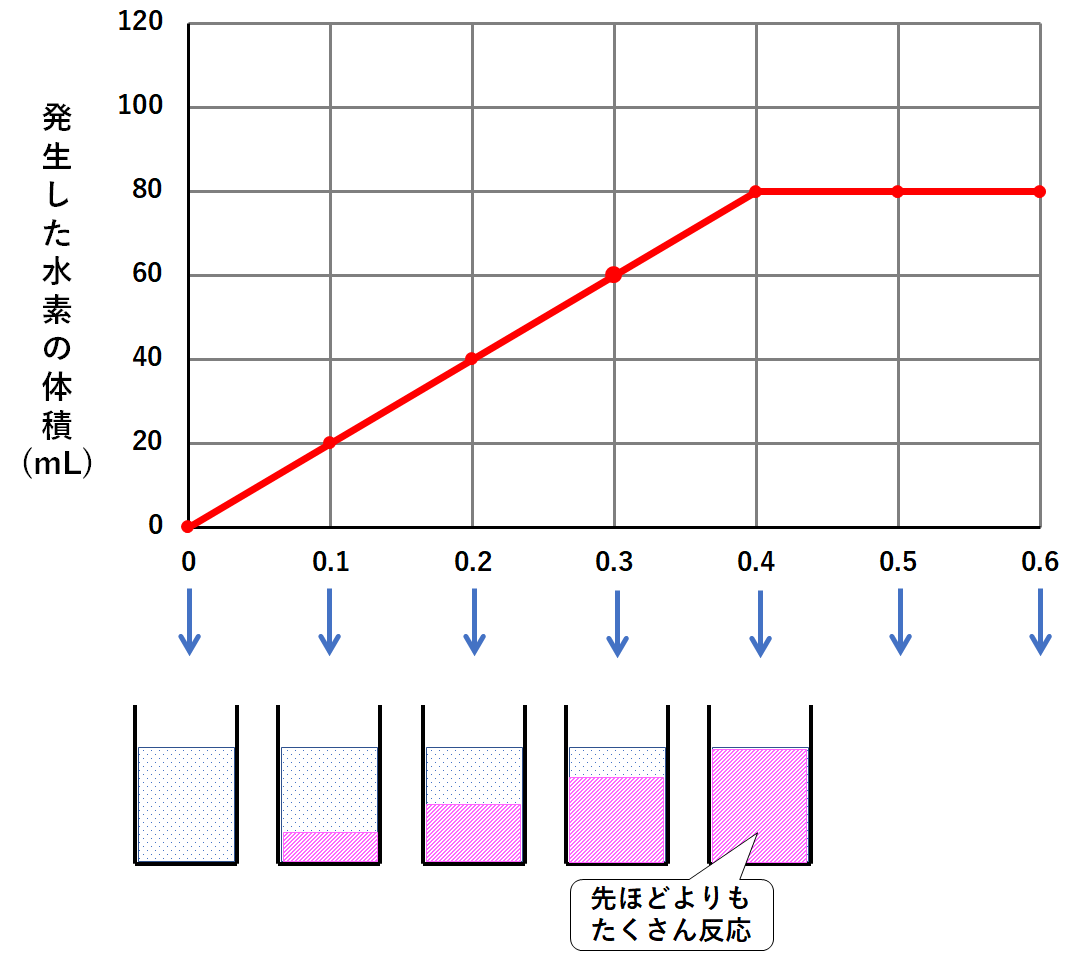
マグネシウム0.5gを加えたとき、塩酸がさらに多く…は反応しませんよね。

0.4gの時点で塩酸がすべて反応していたならば、0.5g加えても結果は同じ。

つまり反応する塩酸の量は0.4gのときと変わりません。(↓の図)

マグネシウム0.6gを加えたときも同じです。

反応する塩酸の量はマグネシウム0.4g、0.5gのときと変わりません。(↓の図)

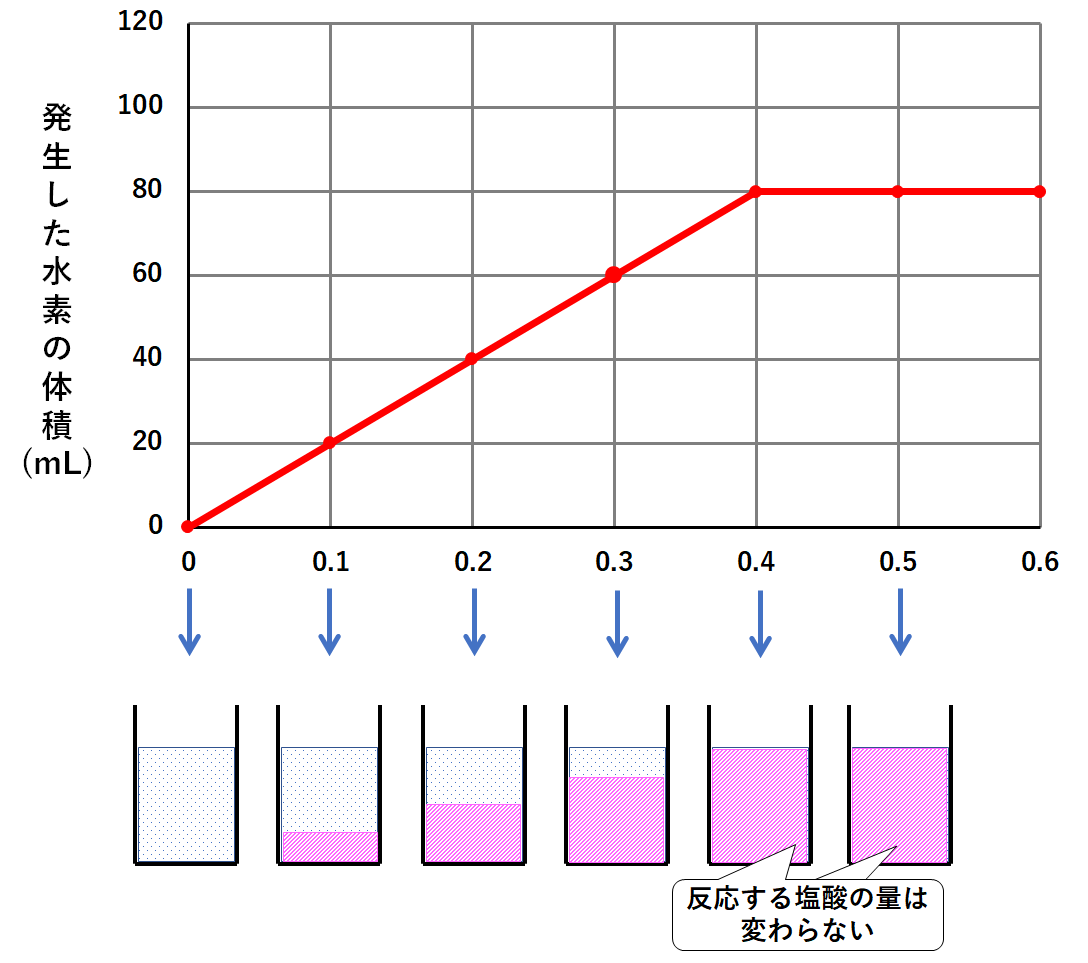
このグラフの一番のポイントは

実験で使った塩酸800mLにはマグネシウム0.4gまでしか反応しない

ということです。

マグネシウムを0.1g・0.2g・0.3g加えたときは、一部の塩酸が反応し、一部の塩酸が余っていた。(↓の図)

マグネシウムを0.5g・0.6g加えたときは、塩酸はすべて反応した。しかしマグネシウムは多すぎたため、マグネシウムの一部が余っていた。(↓の図)

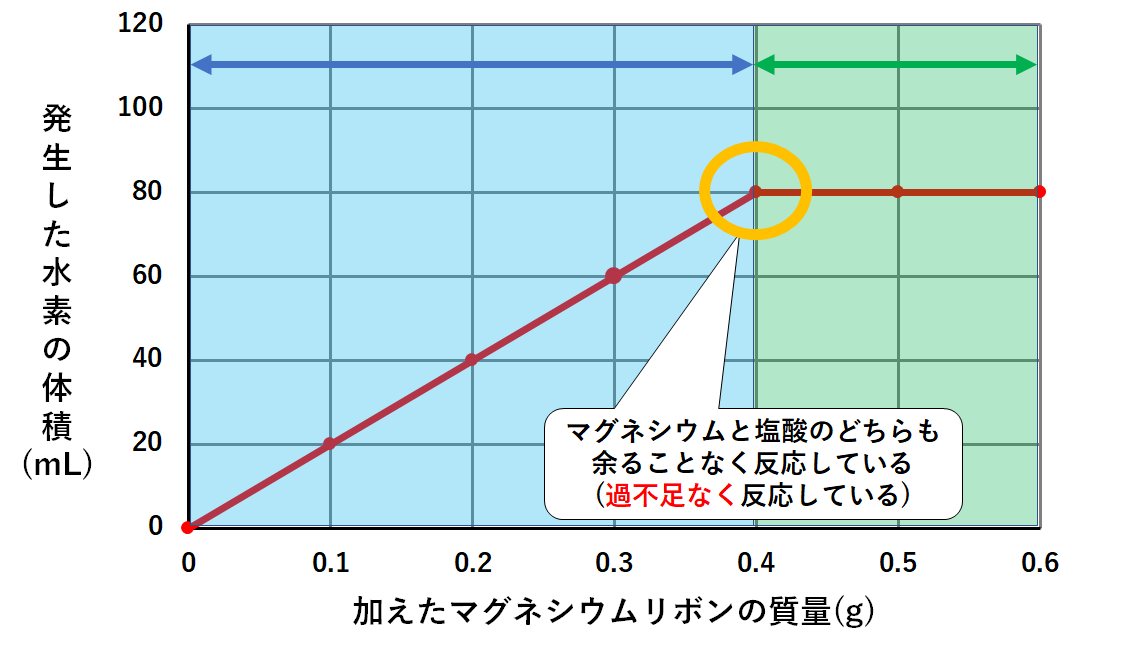
そしてマグネシウム0.4g加えたとき、塩酸はすべて反応した。マグネシウムも余ることがなかった。(↓の図)

このときうすい塩酸とマグネシウムのどちらも余ることなく反応したのです。(これを過不足なく反応した、という言い方をします。)

よってこのときの値を使うと

マグネシウム：塩酸：水素＝0.4g：800mL：80mL

の関係ならば過不足なく反応することがわかります。(塩酸の量は一番最初の問題文に書いてある)

このようにグラフの折れ曲がり点を確認することで、過不足なく反応するときの比がわかります。

「銅：酸素＝4：1」「マグネシウム：酸素＝3：2」のようにどのような比で反応するかは、化学の計算ではもっとも重要です。

いつでも

マグネシウム：塩酸：水素＝0.4g：800mL：80mL

という比になるわけではありません。(覚えても意味ナシ)

問題によってその条件は変わりますから、問題のたびに求めてくださいね。

いまの比を使うと次のような問題が解けます。

例題

(答)

比さえわかっていれば「銅：酸素＝4：1」「マグネシウム：酸素＝3：2」の問題と同じです。

（→【定比例の法則(酸化)】←　を参考に）

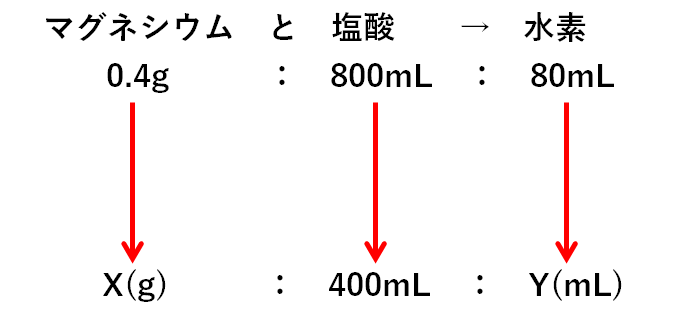
求めるマグネシウムをX(g)とすると

0.4g：800mL＝X(g)：400mL

よりX＝0.2gとなります。

同様に求める水素をY(mL)とすると

800mL：80mL＝400mL：Y(mL)

よりY＝40mLとなります。

※いまは「マグネシウムと塩酸の反応」を例にしましたが、気体を発生させる実験には

・アルミニウムや鉄と塩酸(または硫酸)→水素の発生

・石灰石と塩酸→二酸化炭素の発生

・炭酸水素ナトリウムと塩酸→二酸化炭素の発生

などがあります。

他の問題でも同様の考え方をします。

2．過不足のある計算問題

ここでは先ほどの実験の続きの例題を1つ紹介しましょう。

例題2

(答)

解説に行く前に1つ例を紹介します。

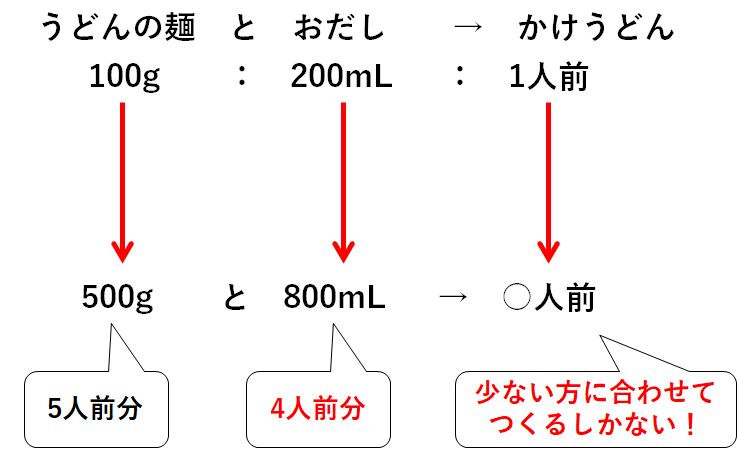
あるうどん屋さんのお話。

そのうどん屋さんではかけうどんが売られています。

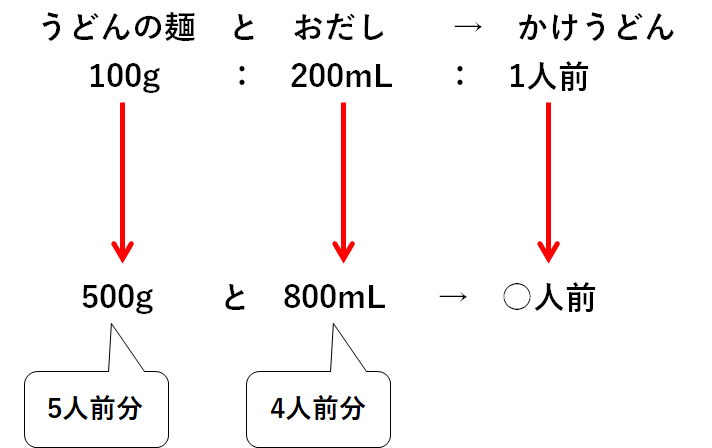
そのかけうどん1人前をつくるには、うどんの麺100gとおだし200mLが必要です。

いま、冷蔵庫を見てみるとうどんの麺が500g、おだしが800mLありました。

さあ何人前のかけうどんをつくれますか？

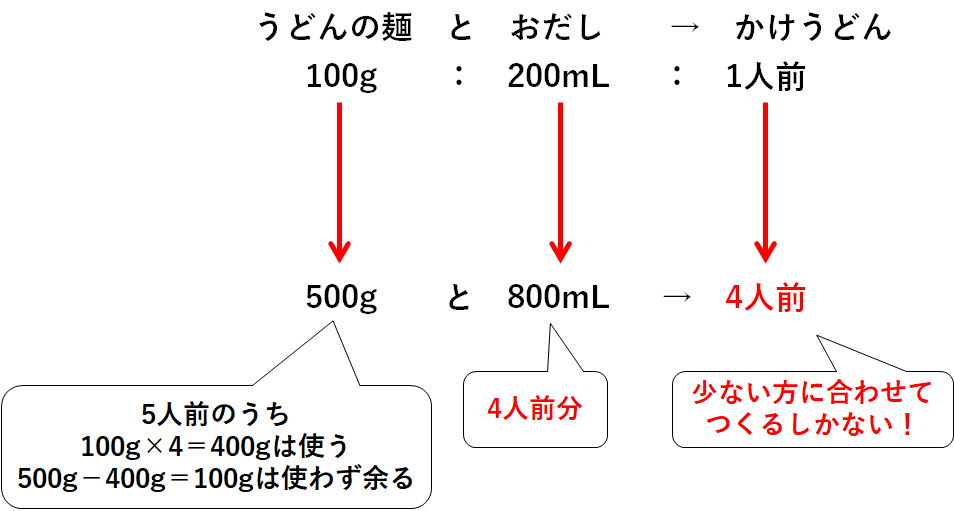
うどんの麺は500g、つまり5人前分あります。

おだしは800mL、つまり4人前分あります。

・うどんの麺500gをすべて使う→おだしが足りないので5人前もつくれない。

・おだし800mLをすべて使う→4人前のかけうどんしかつくれない。

つまり最大で4人前までしかつくれないのです。

うどんの麺とおだし、少ない方に合わせて作るしかないのです。

ちなみにうどんの麺は一部が余ってしまいます。

化学の計算でも同じことが起こります。

マグネシウム：塩酸：水素＝0.4g：800mL：80mL

の比で反応が起こりました。

水素80mLつくるには、マグネシウム0.4gと塩酸800mL必要なのです。

かけうどん→水素

うどんの麺→マグネシウム

おだし　　→塩酸
と置き換えていると考えてください。

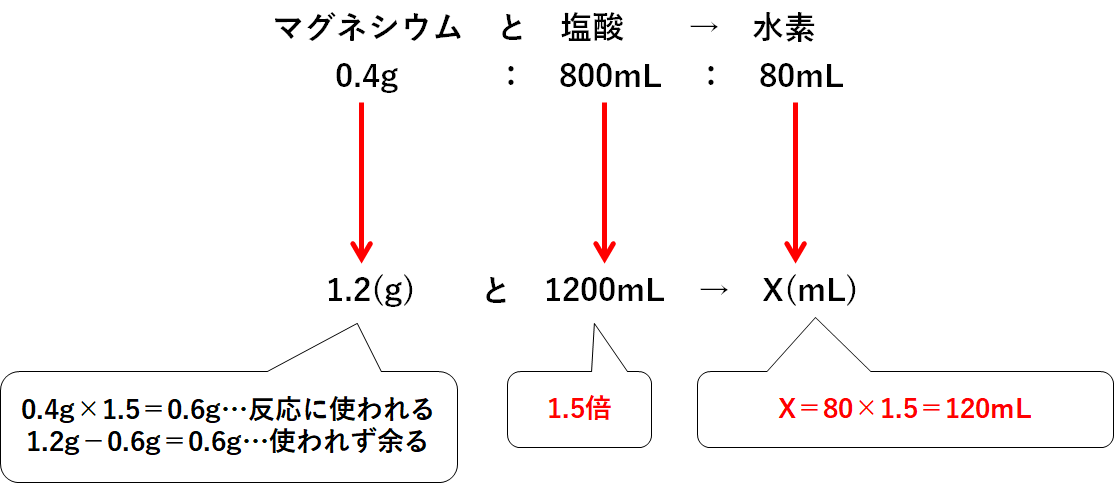
いま問題では塩酸1200mLとマグネシウムリボン1.2gを反応させました。

つまり塩酸は1.5人前、マグネシウムは3人前あるのです。(↓の図)

少ない方(いまは塩酸)に合わせてかけうどん(＝水素)をつくるしかないので、発生する水素は↓のようになります。

またこの反応ではマグネシウムが多すぎて、一部が反応せずに余ります。
その質量は↓のようになります。

よって

(1)・・・120mLの水素が発生

(2)・・・マグネシウムが0.6g反応せずに余る

となります。

このように2つのものを反応させてどちらかが余るかもしれない、そんな問題では

もとの比から何倍になっているかを比べ、数字の小さい方に合わせて計算する

のが鉄則です。