化合について・・・→【化合】←
分解について・・・→【分解】←
酸化について・・・→【酸化と燃焼】←
還元について・・・→【還元】←
その他の化学変化の計算については
→【質量保存の法則】← または →【定比例の法則(酸化)】← または →【気体の発生に関する計算】←
化学反応式について・・・→【化学反応式】←
で解説しています。
1.酸化銅の炭素による還元
■還元とは
酸化物から酸素がうばわれる反応を還元という。
つまり酸化とは正反対の反応。
※還元について詳しいことは→【還元】←を参考に。
もっとも出題されやすい還元反応の例は
酸化銅の炭素による還元
です。
※酸化銅の炭素による還元とは
反応の様子: 酸化銅+炭素→銅+二酸化炭素
化学反応式: 2CuO + C → 2Cu + CO2
酸化銅から酸素をうばっているのは炭素です。
炭素は酸化銅がもっていた酸素と結びつき、二酸化炭素になります。
この反応に関する計算問題について解説していきます。
2.酸化銅の還元に関する計算問題
例題
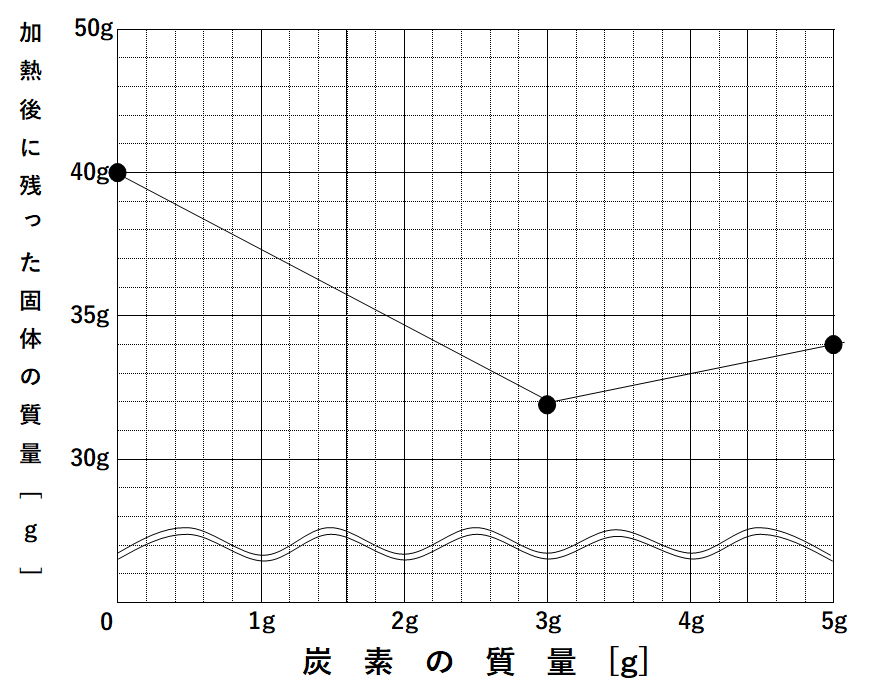
40gの酸化銅とさまざまな質量の炭素の粉末を混ぜ合わせて↓の図のような装置で加熱した。
このとき炭素の粉末の質量と試験管に残った固体の質量との関係をグラフにすると↓のようになった。
(1) 酸化銅40gをすべて還元するには何gの炭素が必要か。
(2) 酸化銅40gと炭素を過不足なく反応させたとき、発生する二酸化炭素は何gか。
(3) 酸化銅2.0gと過不足なく反応する炭素は何gか。このとき生じる二酸化炭素は何gか。
(4) 酸化銅80gと炭素12gを反応させたとき、試験管に残る固体の質量は何gか。
(5) 酸化銅120gと炭素6gを反応させたとき、試験管に残る固体の質量は何gか。
まず、与えられたグラフの意味はわかりますか?
このグラフが示すことの意味を考えましょう。
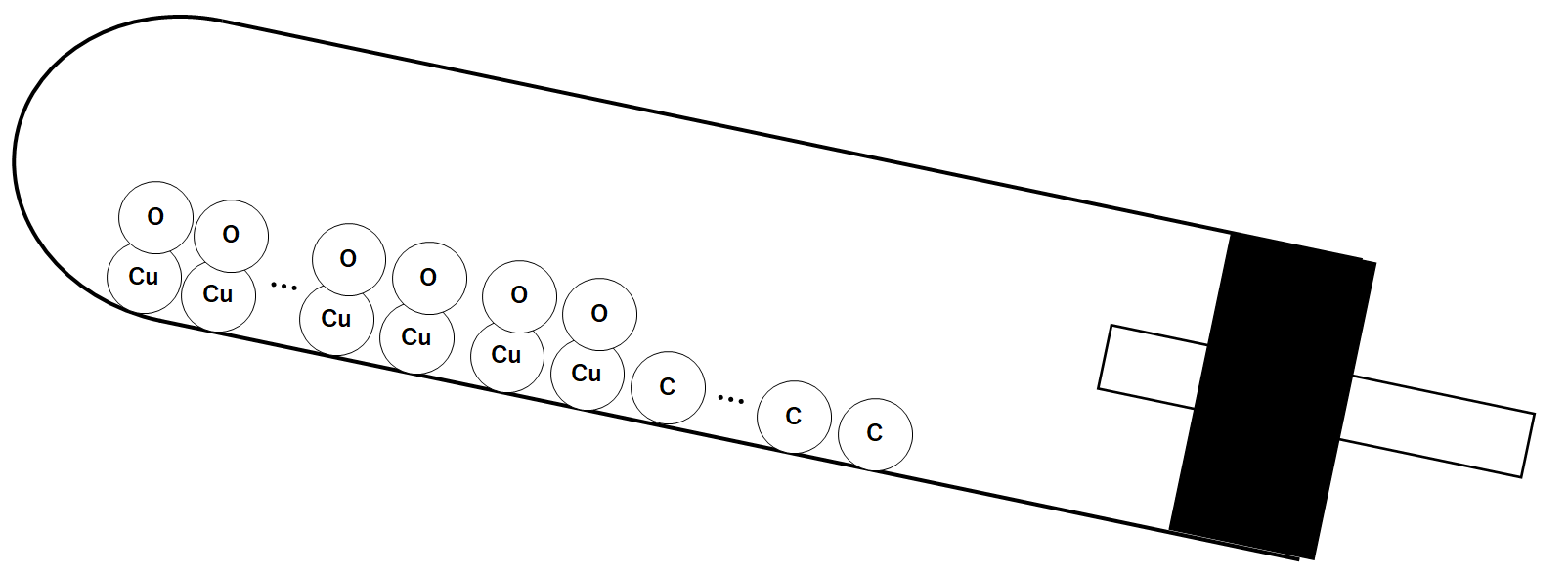
試験管の中では還元が起こっています。
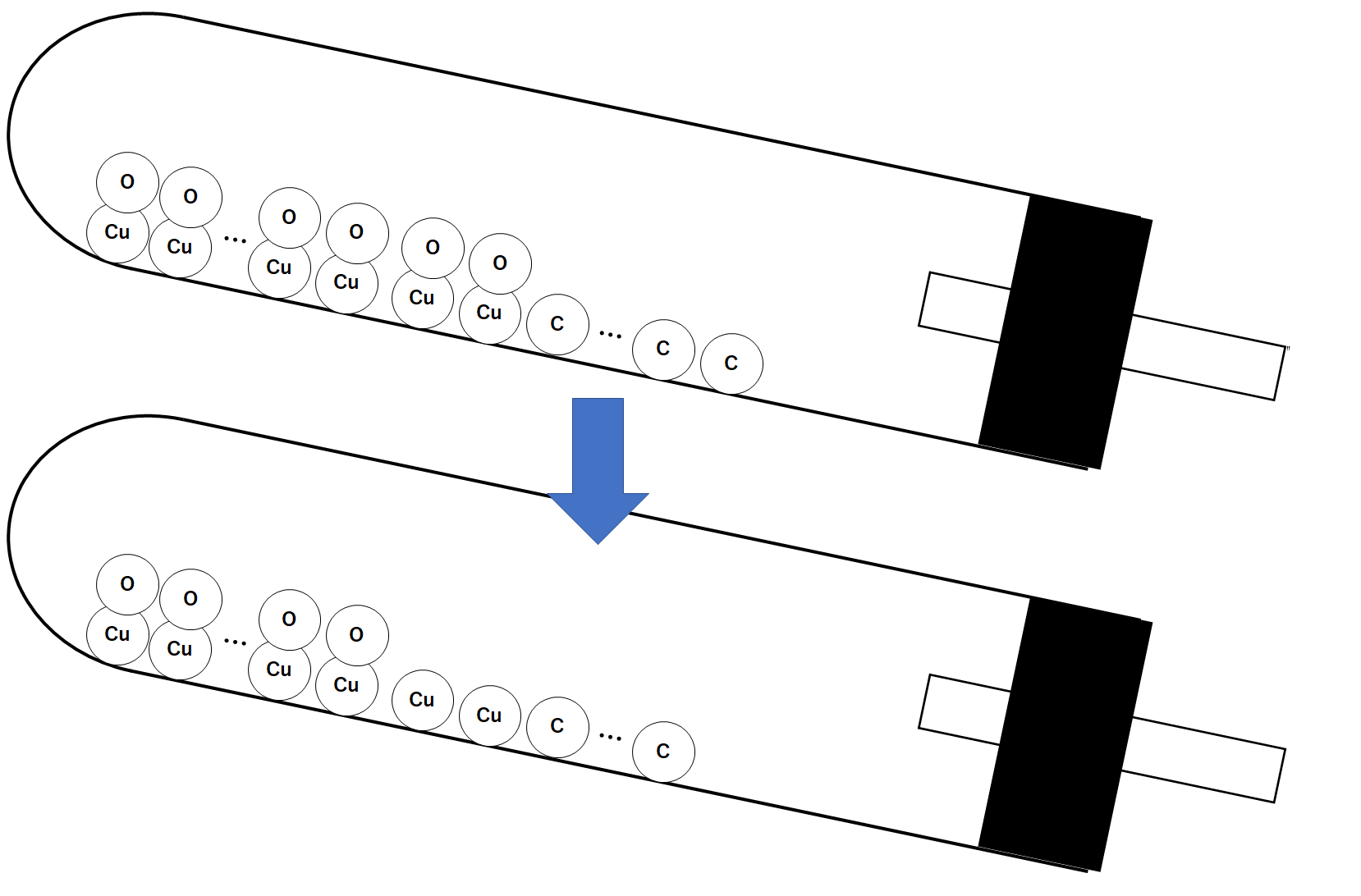
その様子を模式的に表します。(↓の図)
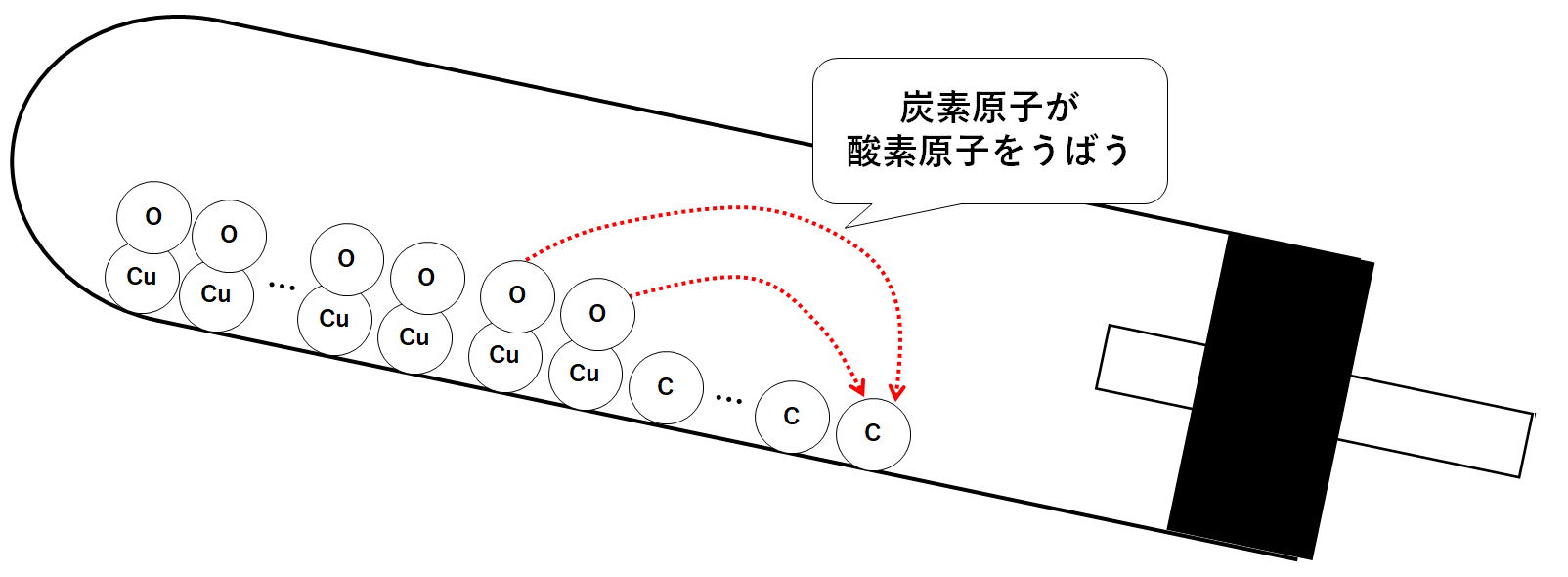
加熱すると炭素原子が、酸化銅に含まれる酸素原子をうばっていきます。(↓の図)
炭素原子は、うばった酸素原子と結びついて二酸化炭素分子になります。(↓の図)
二酸化炭素分子は石灰水へと入り込むため、試験管内の質量は減少していくことになります。(↓の図)
グラフを見たとき、
炭素粉末を増やすほど「試験管に残る固体の質量(縦軸)」は減少しています。(↓の図)
炭素粉末を増やすほどうばわれる酸素が増えるため、「試験管に残る固体の質量(縦軸)」は減少していくのです。
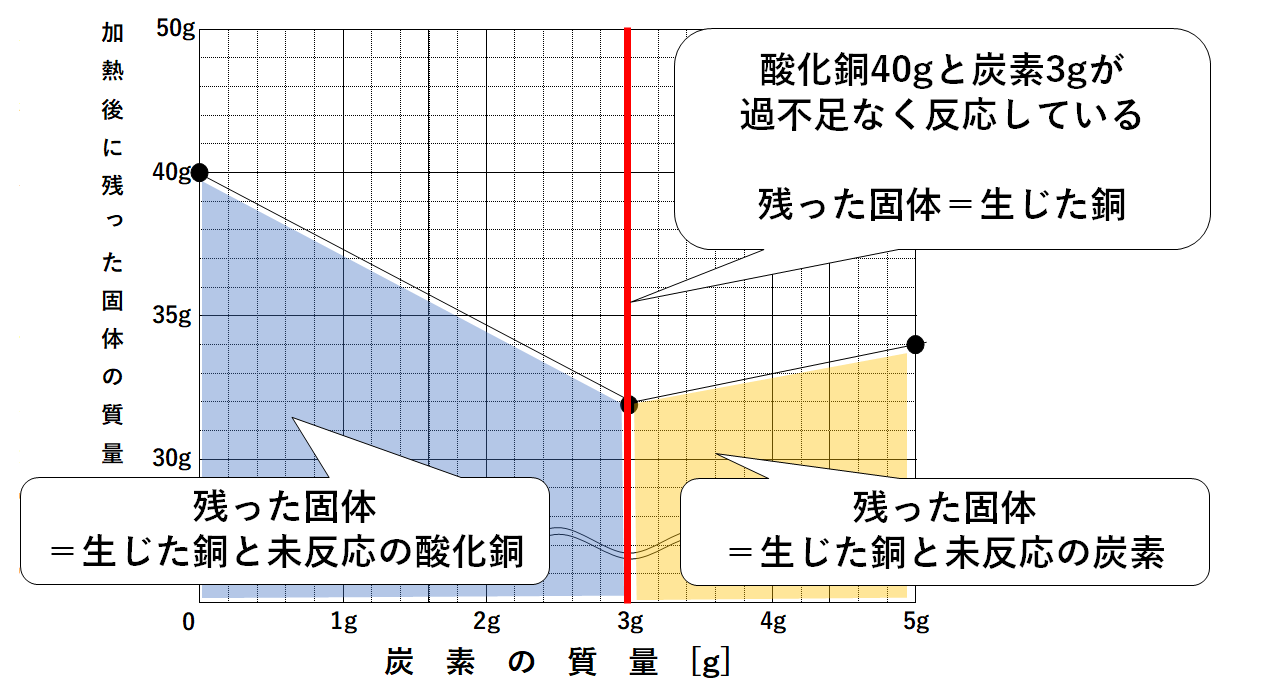
グラフより、「試験管に残る固体の質量(縦軸)」が最も小さくなるのは
炭素粉末を3g加えたとき。
このとき、すべての酸化銅から酸素をうばった(=すべての酸化銅を還元した)ことがわかります。(↓の図)
グラフから
・40gの酸化銅をすべて還元するには、炭素が3g必要。
・酸化銅をすべて還元したとき、試験管に残る固体は銅のみ。
・その銅の量は32g。
とわかります。
よって酸化銅を炭素で還元したときの質量比は
となります。
が、二酸化炭素の質量がわかっていません。
二酸化炭素の量を求めるには質量保存の法則を使います。
質量保存の法則とは・・・
化学変化の前後で、質量の総和は変わらない。※詳しくは→【質量保存の法則】←を参考に。
反応前、酸化銅と炭素合わせて
40+3=43g
あるので
二酸化炭素は
43-32=11g
発生したとわかります。
(答)
ではここから例題の答えを求めます。
(1)
グラフより3gが正解です。
(2)
先述の計算より11gの二酸化炭素が発生しました。
(3)
ここまでで、この反応において
という比で反応することがわかっています。
この比を利用して比例式を解きましょう。
求める炭素をx(g)とします。
酸化銅と炭素の比が40:3であることに注目して
40:3=2.0g:x(g)
これを解いてx=0.15g
となります。
求める二酸化炭素をy(g)とします。
酸化銅と二酸化炭素の比が40:11であることに注目して
40:11=2.0g:y(g)
これを解いてy=0.55g
となります。
よって炭素は0.15g・二酸化炭素は0.55gとなります。
(4)
「酸化銅80gと炭素12g」で実験を行うわけですが、
酸化銅と炭素、どちらも余ることなく反応するとは限りません。
ここでは次のような例を考えます。
あるうどん屋さんのお話。
そのうどん屋さんではかけうどんが売られています。
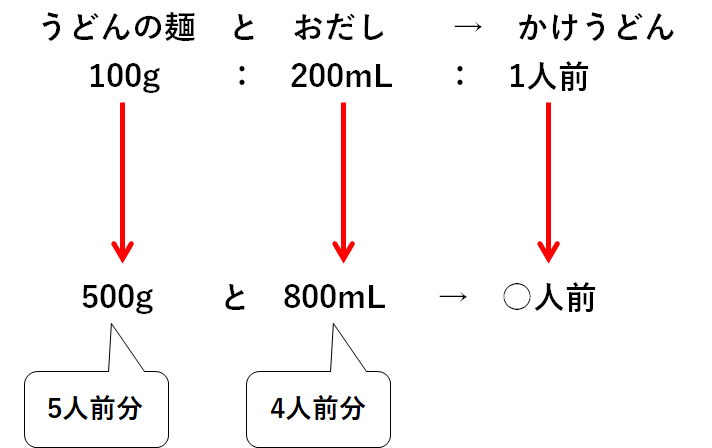
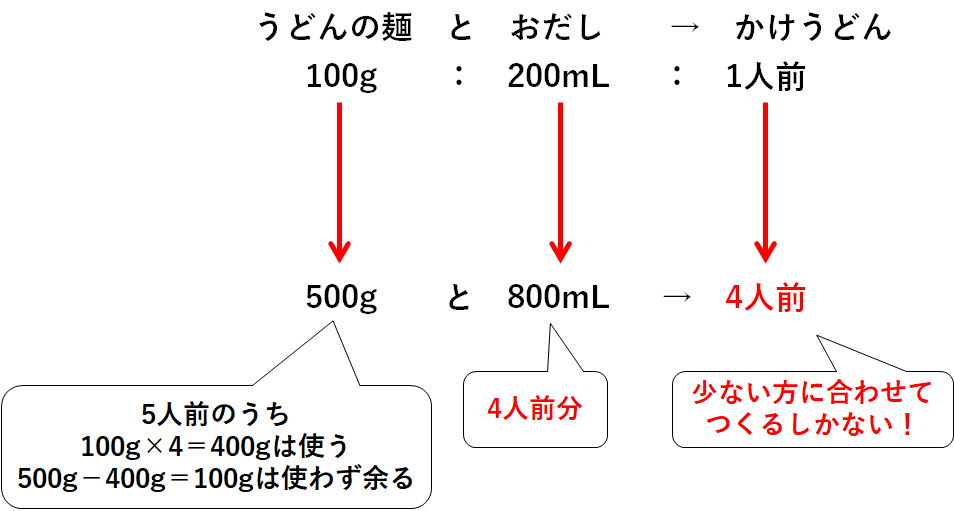
そのかけうどん1人前をつくるには、うどんの麺100gとおだし200mLが必要です。
いま、冷蔵庫を見てみるとうどんの麺が500g、おだしが800mLありました。
さあ何人前のかけうどんをつくれますか?
うどんの麺は500g、つまり5人前分あります。
おだしは800mL、つまり4人前分あります。
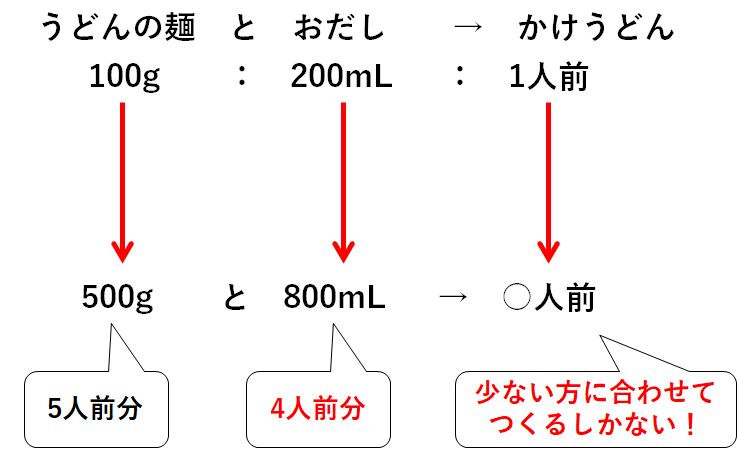
・うどんの麺500gをすべて使う→おだしが足りないので5人前もつくれない。
・おだし800mLをすべて使う→4人前のかけうどんしかつくれない。
つまり最大で4人前までしかつくれないのです。
うどんの麺とおだし、少ない方に合わせて作るしかないのです。
ちなみにうどんの麺は一部が余ってしまいます。
化学の計算でも同じことが起こります。
反応の際に、少ない方に合わせて物質が生成するのです。
話を戻しましょう。
過不足なく反応するときの比は
でした。
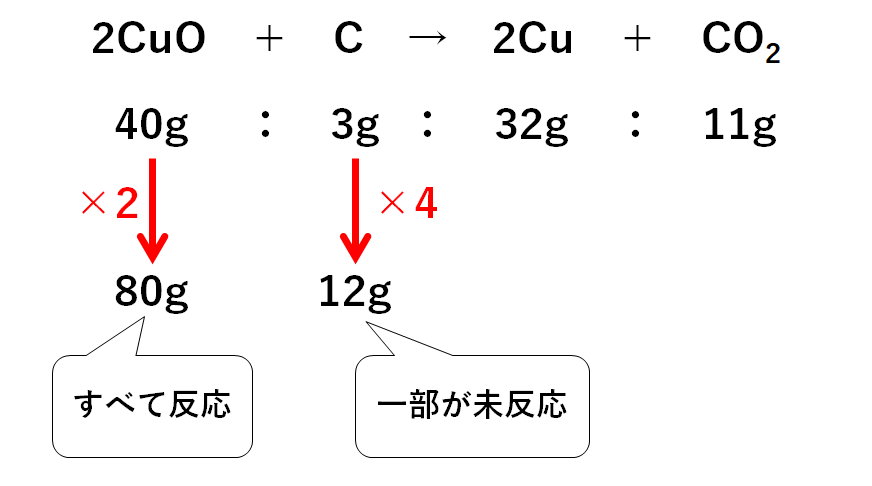
そしてこの問いでは「酸化銅80gと炭素12g」で実験を行います。
よって酸化銅はすべて反応し、炭素は一部反応せず、余ることがわかります。
(酸化銅は2人前、炭素は4人前あるため、2人前分しか反応しない)
反応によって生じる銅は
32g×2=64g (2人前しか反応しないため)
また反応に使われる炭素は
3g×2=6g (2人前しか反応しないため)
よって未反応で余っている炭素は
12g-6g=6g
試験管には生じた銅と、未反応のまま余った炭素が残っているので、その合計は
64g+6g=70g
となります。
よって試験管に残る固体の質量は70gとなります。
(5)
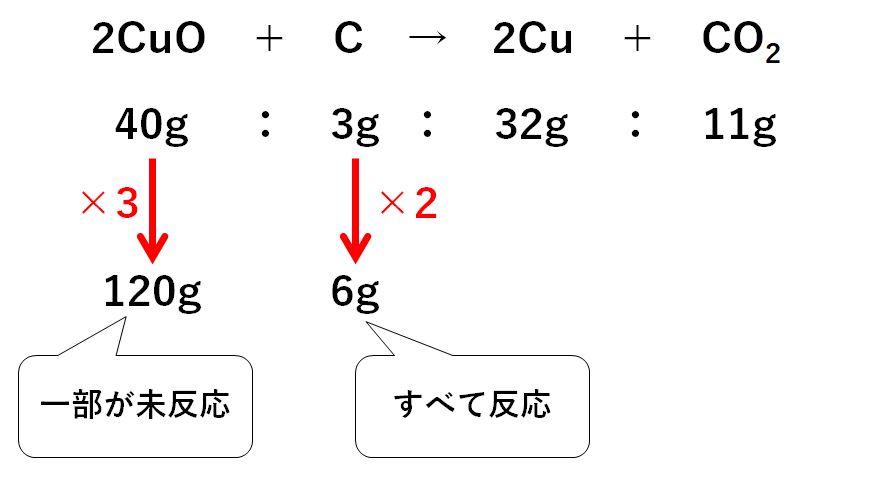
「酸化銅120gと炭素6g」で反応を起こしています。が、すべて余ることなく反応するかはわかりません。
元の比の何倍になっているか(何人前か)を調べて、どちらがあまり、どちらがすべて反応するかを調べます。
酸化銅は3人前、炭素は2人前あるので、
酸化銅は一部が未反応のまま余り、炭素はすべて反応することがわかります。
(2人前分しか反応は起こらない)
反応によって生じる銅は
32g×2=64g (2人前しか反応しないため)
また反応に使われる酸化銅は
40g×2=80g (2人前しか反応しないため)
よって反応せず、余っている酸化銅は
120g-80g=40g
試験管には生じた銅と、未反応のまま余った酸化銅が残っているので、その合計は
64g+40g=104g
となります。
よって試験管に残る固体の質量は104gとなります。
POINT!!
過不足のある計算では・・・
・反応するときの質量比を求めておく
・それそれの物質が、その比の何倍分反応あるのかチェック
・少ない方に合わせて計算(倍率の小さい方)







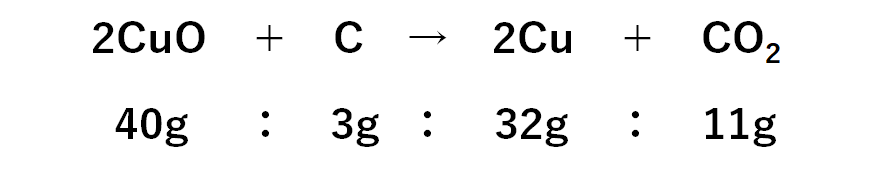

コメント(承認された場合のみ表示されます)
ありがとうございますよくわかりました。
山﨑様
コメントありがとうございます。
お役に立てたようで嬉しい限りです。
これからもいつでもご利用ください。
すごくわかりやすい解説です。他のも拝見させていただきます。
高校受験生様
コメントありがとうございます。
ありがたいお言葉をいただき、うれしいです。
またいつでもご覧くださいね。