*このページは「自家受粉とは」や「自家受粉を繰り返し行った場合の遺伝」といった発展的な内容を含みます。
遺伝の基本については→【遺伝の規則性】←を参考に。
1．自家受粉による遺伝
自分のめしべに自分のおしべの花粉をつけること。
エンドウを例に考えましょう。
エンドウの種子には丸としわの2つの形がありました(対立形質)。
まず
丸い種子をつくる純系のエンドウ【ア】(AAの遺伝子をもつ)
と
しわ有り形の種子をつくる純系のエンドウ【イ】(aaの遺伝子をもつ)
を受粉させましょう。
できる子世代【ウ】はすべてAaの遺伝子をもちます。
つまり丸い種子をつくるエンドウのみができます。(丸の方が顕性形質）
ではここで子世代【ウ】を自家受粉させます。
つまり子世代【ウ】の1つのエンドウの花に注目して、
その花のめしべに同じ花の花粉を受粉させます。
すべての個体でこれを行うのです。
遺伝子でいうと
AaとAa
のかけ合わせです。
できる孫世代【エ】の遺伝子はAA：Aa：aa＝1：2：1となっています。
つまり丸：しわ＝3：1となるようにエンドウができます。
この孫世代【エ】のエンドウが4本しかなかったとしましょう。
AA：Aa：aa＝1：2：1なので
①遺伝子がAAのものが1本
②遺伝子がAaのものが2本
③遺伝子がaaのものが1本
という数のエンドウがあることになります。
この4本を自家受粉させます。
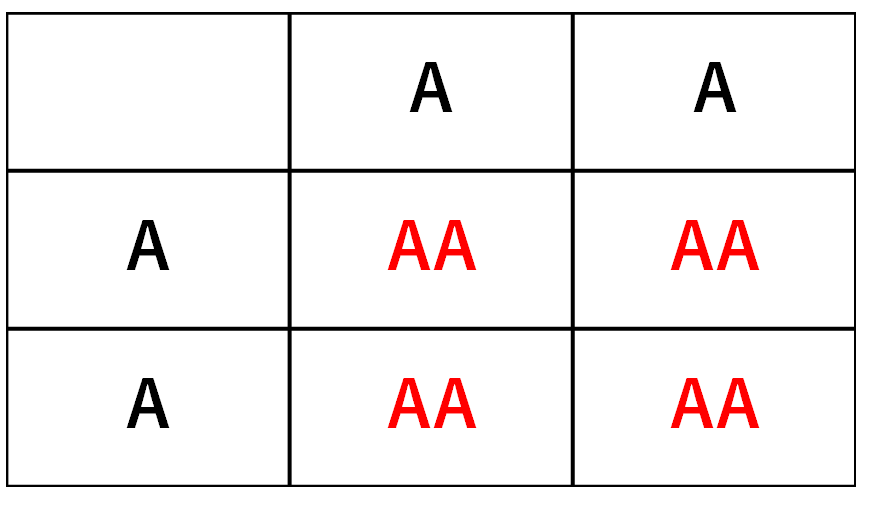
①遺伝子がAAのものを自家受粉
要は AAとAA のかけ合わせです。
AA：Aa：aa＝4：0：0
の割合で子が生まれますね。
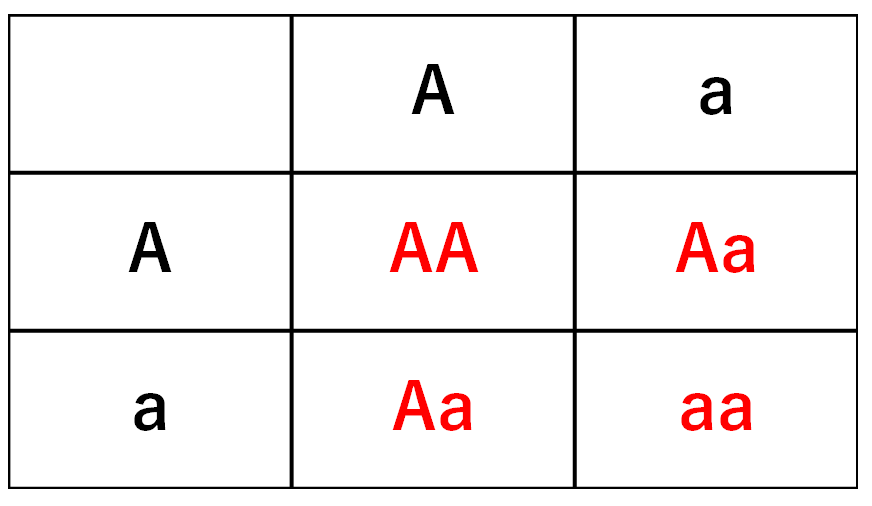
②遺伝子がAaのものを自家受粉
要は AaとAa のかけ合わせです。
AA：Aa：aa＝1：2：1
の割合で子が生まれますね。
③遺伝子がaaのものを自家受粉
要は aaとaa のかけ合わせです。
AA：Aa：aa＝0：0：4
の割合で子が生まれますね。
まとめると↓の図のようになります。
ここで図の②について、なぜ2つ書いているのか。
①は1本、③は1本に対して②はエンドウが2本存在するためです。
つまりAA：Aa：aa＝6：4：6＝3：2：3となります。(↓の図)
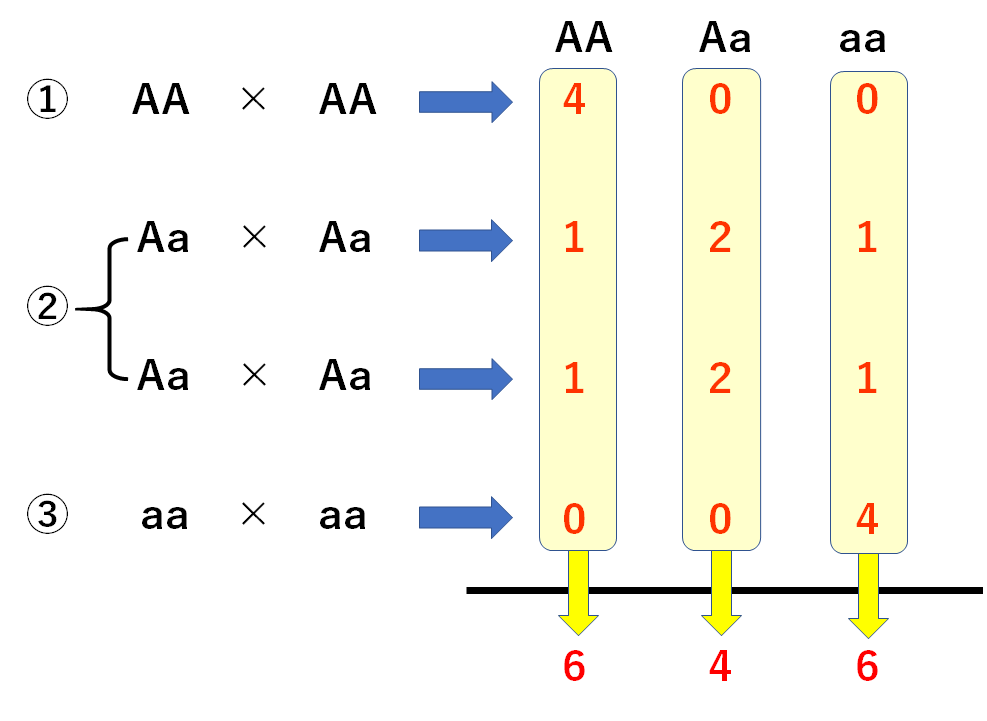
形質でいうと丸：しわ＝5：3となります。
例題
エンドウの種子の形を丸にする遺伝子をA、しわにする遺伝子をaとする。
いま、エンドウの集団【ア】とエンドウの集団【イ】がある。
集団【ア】・・・すべてAaの遺伝子をもち、200本のエンドウが存在する。
集団【イ】・・・すべてaaの遺伝子をもち、100本のエンドウが存在する。
集団【ア】【イ】を親世代とし、それぞれ自家受粉させる。
このときにできる子世代のエンドウから得られる種子の形はどのようになっているか簡単な整数比で表せ。
(答)
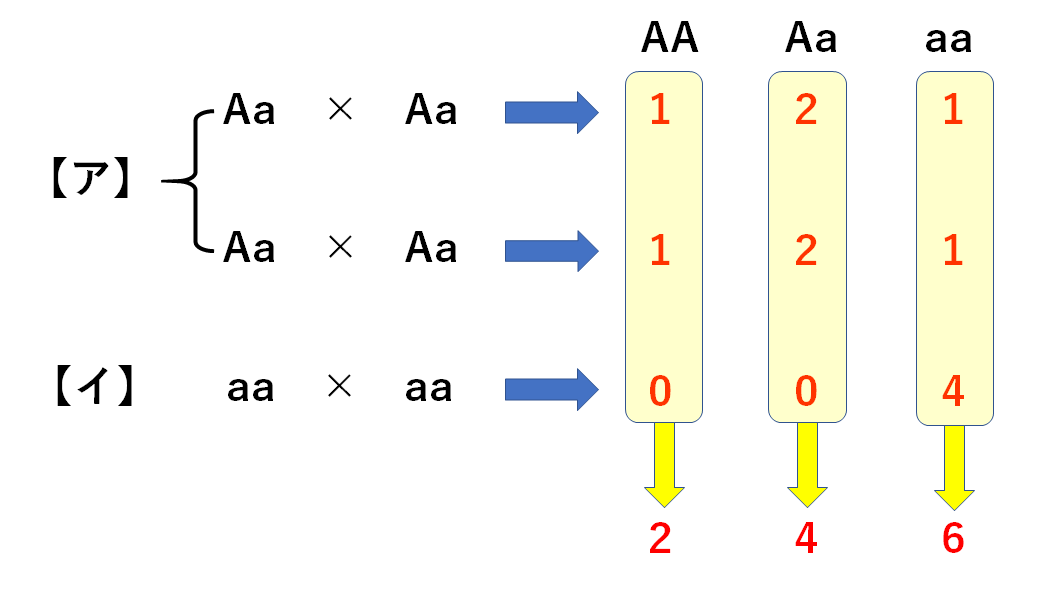
まず集団【ア】のエンドウは集団【イ】よりも2倍多いですね。
集団【ア】のエンドウが自家受粉すると
Aa×Aaのかけ合わせなので
AA：Aa：aa＝1：2：1
の割合で子のエンドウが得られます。
また
集団【イ】のエンドウが自家受粉すると
aa×aaのかけ合わせなので
AA：Aa：aa＝0：0：4
の割合で子のエンドウが得られます。
まとめると↓のようになります。
ここで【ア】を2つ書いているのは【ア】が【イ】よりも2倍多いからです。
よって
AA：Aa：aa＝2：4：6＝1：2：3
となります。
つまり子のエンドウから得られる種子は
丸：しわ＝3：3＝1：1
の割合で得られると考えられます。
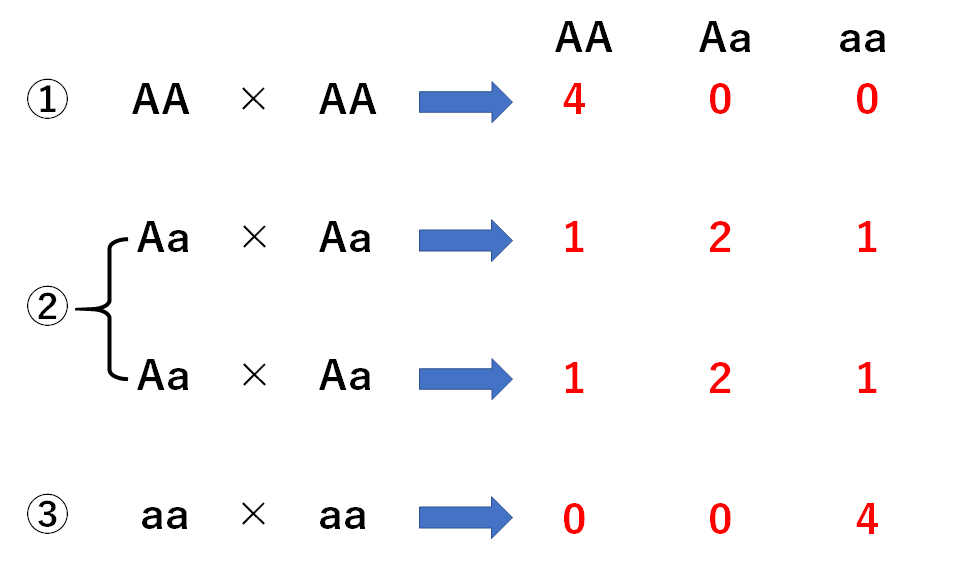
自家受粉の問題を解くコツは
かけ合わせが以下の3通りしかありえないということを理解しておくことです。
AA×AA → AA：Aa：aa＝4：0：0
Aa×Aa → AA：Aa：aa＝1：2：1
aa×aa → AA：Aa：aa＝0：0：4
自分のめしべに自分の花粉をつけるのですから
Aa×AAやAa×aaのような異なる遺伝子の組のかけ合わせなどありえないのです。
あとはこれに存在比率・存在比（さっきの例題では【ア】200本・【イ】100本で【ア】が【イ】の2倍存在する）を考慮すればよいということです。
コメント(承認された場合のみ表示されます)
いいのでわないか
中田翔様
コメントありがとうございます。
理解に役立った、ということでしょうか？
もしお役に立てているのであれば、とてもうれしいことです。
また是非ご覧ください。