このページは後半に発展的な内容を含みます。
月に関する基本的なことは→【月の満ち欠け】←を参考に。
1．月の公転周期
■月の公転と公転周期
月は地球の衛星であるので、地球を中心に公転している。
その公転にかかる時間(公転周期)は約27.3日である。
2．月の自転周期と公転周期
■月の自転周期
月にも地軸が存在し(目に見えない)、地軸を中心に自転している。
その自転にかかる時間(自転周期は)約27.3日である。(公転周期と同じ)
月は自転周期と公転周期が同じです。
例えば月が90度自転したとすると、同時に90度公転していることになります。
このことから月はいつも同じ面を地球に向けています。
(言い換えると、地球からはいつも同じ面が見えています。)
*ここから先は発展的な内容を含んでいます。
3．*月の1日の動き
ここでは月の公転周期がおよそ30日として考えます。
(本当は27.3日で360度動くが、30日で360度と考える。)
ということは、月は1日で12度公転することになります。
(360度÷30日＝12度)
いま↓のように太陽・地球・月があるとします。
この月は真夜中0:00の地点で南中して見えます。(↓の図)
ここから1日後、月は12度公転します。(↓の図)
※本来は地球も太陽のまわりを1度公転していますが、いまは無視します。
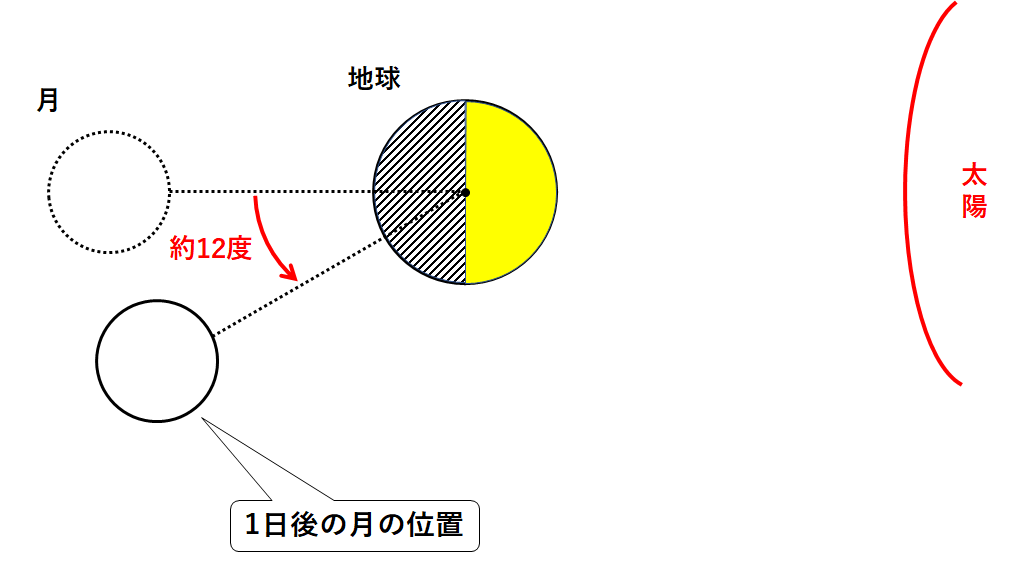
この月が南中して見えているという観測者。
先ほど南中して見えた位置より12度離れた地点です。
この地点は0:48であると考えられます。(↓の図)
(地球の自転は1時間で360度⇒1時間で15度⇒4分で1度・・・48分で12度)
この月の公転は↓のように観測者から見て東の空へと動いています。
よって
・1日あたりで南中時刻は約50分遅くなる。
・月の公転によって西の空から東の空へ動いて見える。
ということがわかります。
4．月の満ち欠けの周期
ここでは再び月の公転周期を27.3日として考えます。
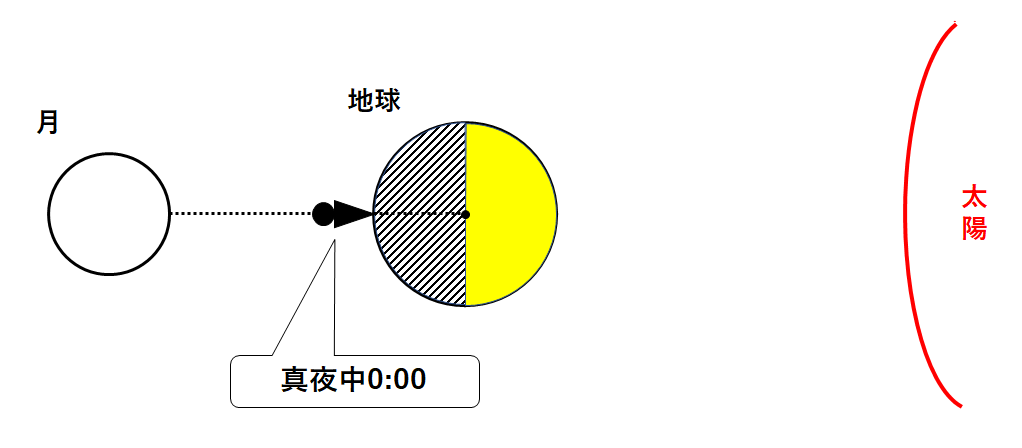
いま次のように満月の位置に月があるとします。
次に満月が観測できるのは何日後かを求めます。
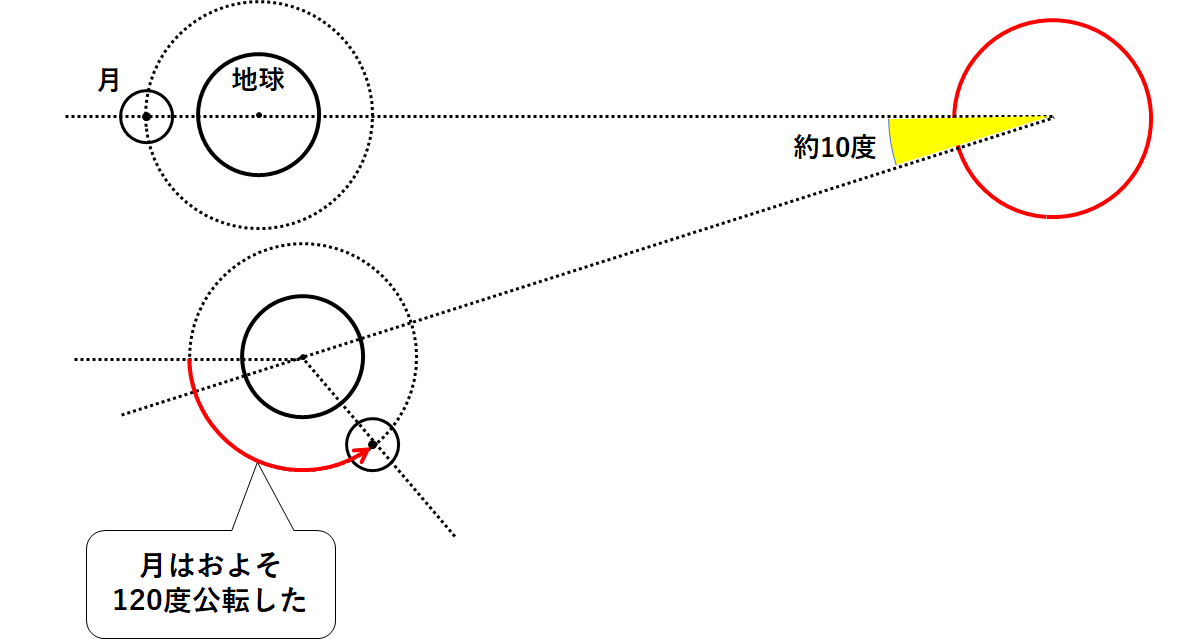
例えば、先ほどの図の位置から10日後。
地球は太陽のまわりを10度公転します。(↓の図)
(地球の公転は1年で360度⇒1ヶ月で30度⇒1日で1度)
一方で月は約120度公転します。(↓の図)
(1日で約12度公転していると仮定した数値なので実際の数値とはずれがあります)
このように月が公転すると同時に地球も公転しています。
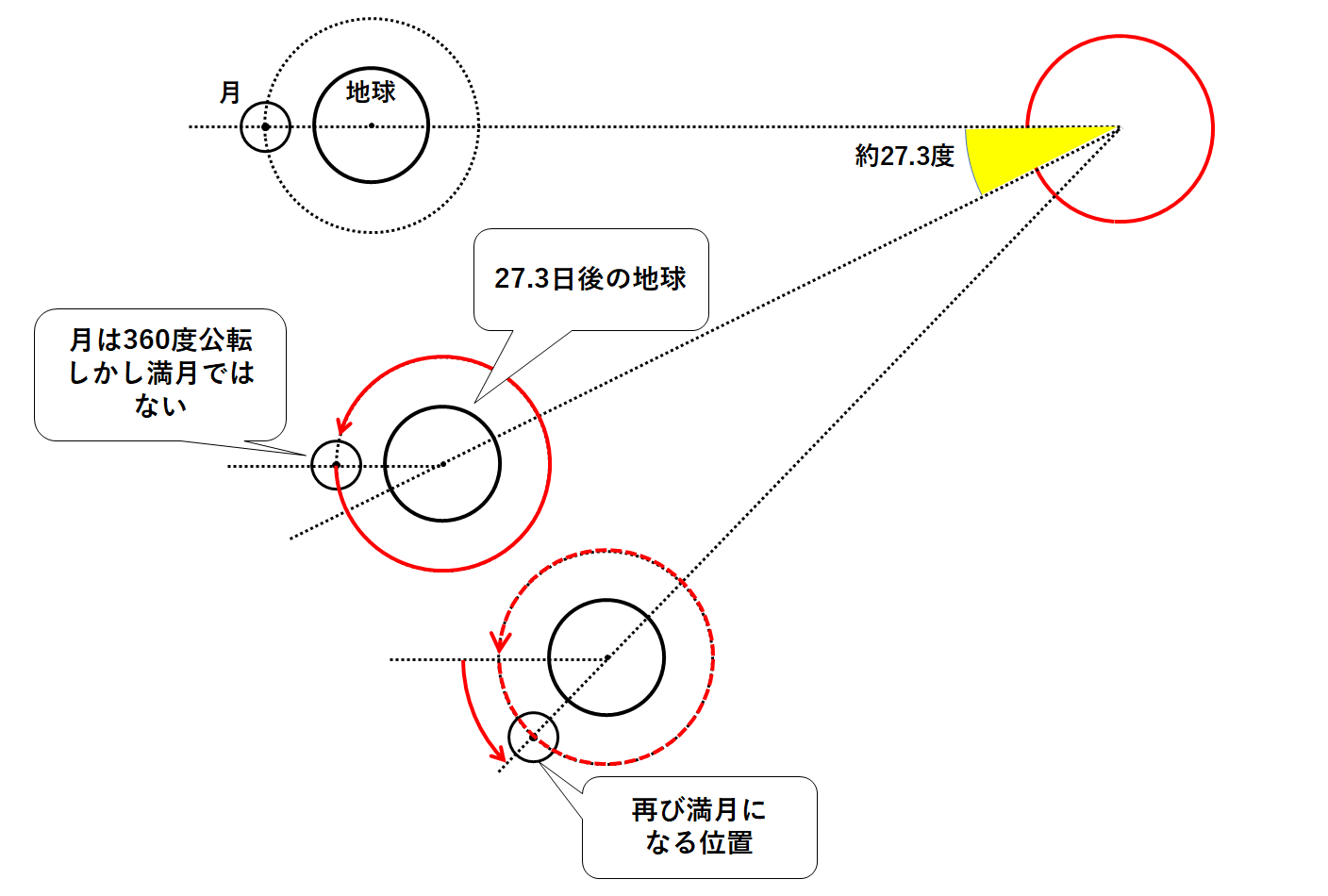
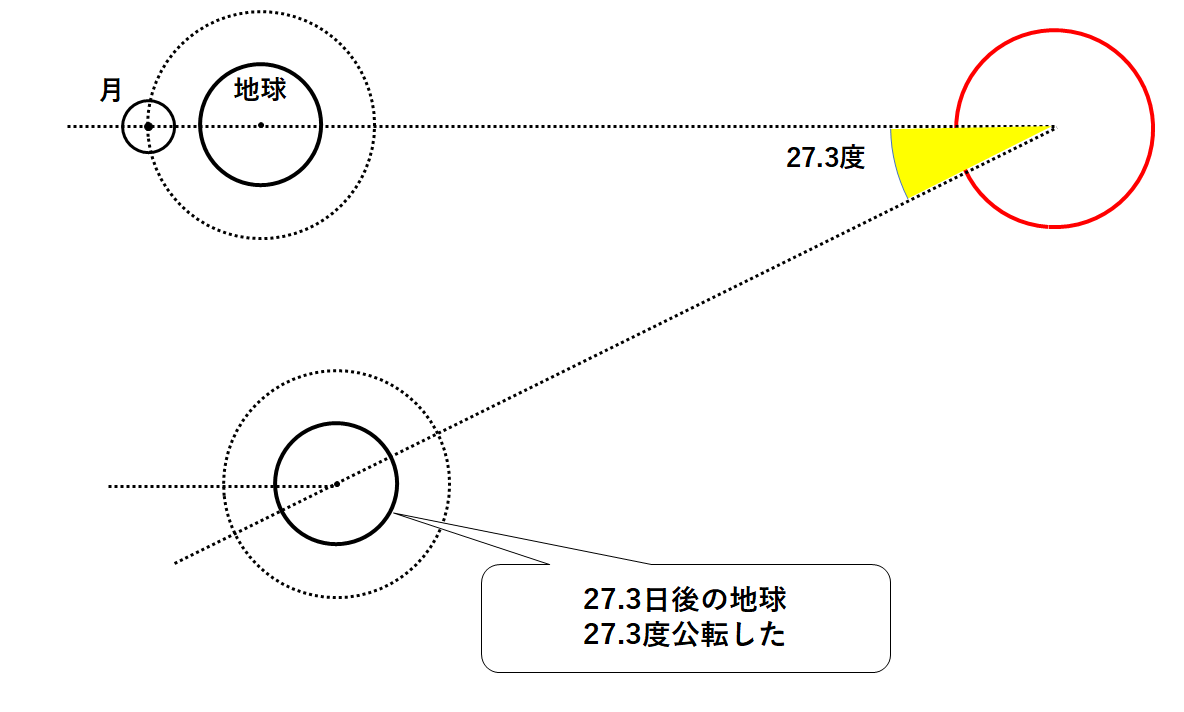
でははじめの位置から27.3日後。
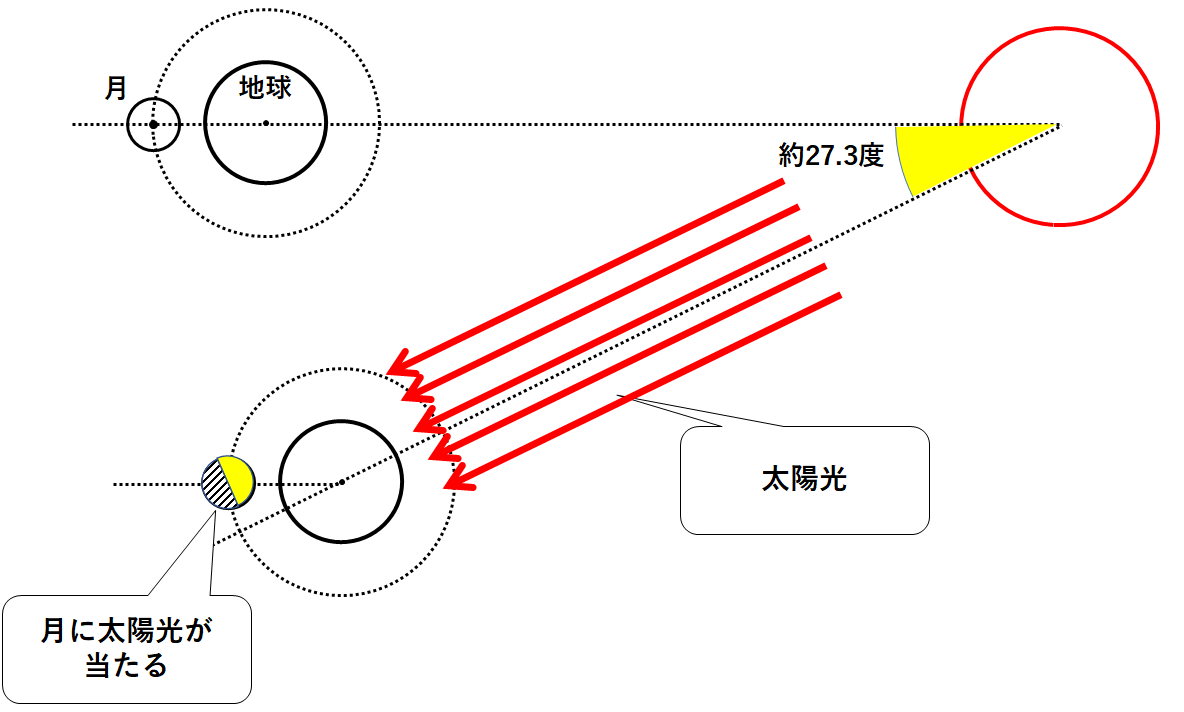
地球は太陽のまわりを27.3度公転します。(↓の図の黄色の角)
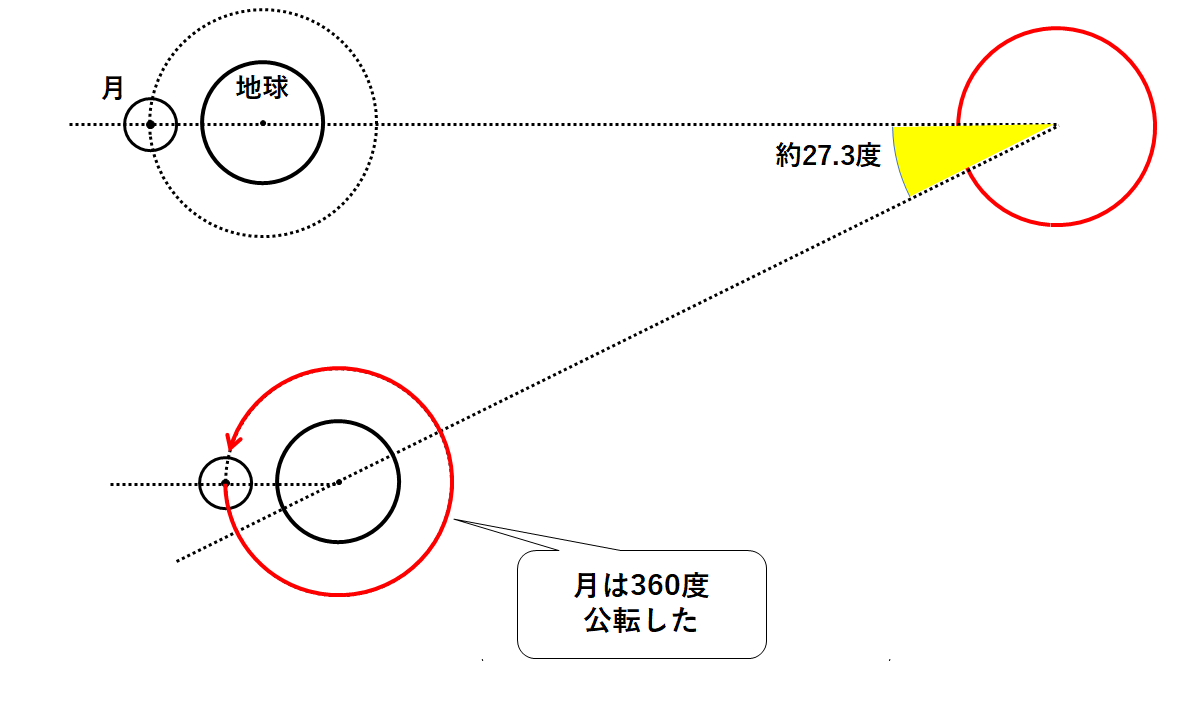
一方で月は360度公転します。(↓の図)
(月の公転周期は27.3日であるため。)
ここで太陽からの光が月にあたる様子を見てみます。(↓の図)
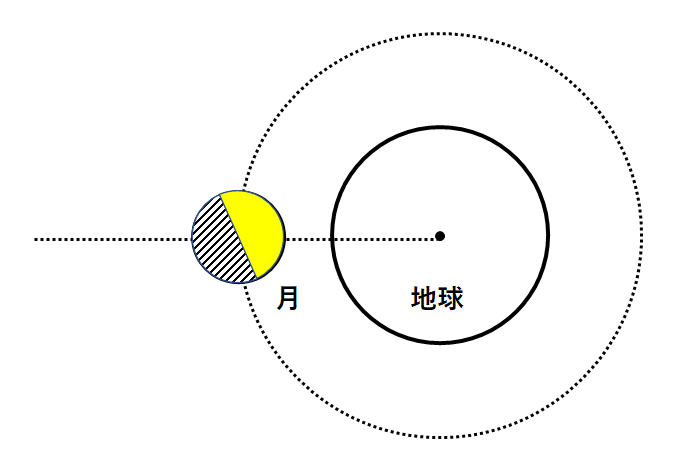
この図の中でも地球付近だけ取り出します。(↓の図)
地球から見るとこの月はどのような形に見えるか。
(考え方は→【月の満ち欠け】←を参考に)
以下のように左隅だけが欠けた形に見えます。(↓の図)
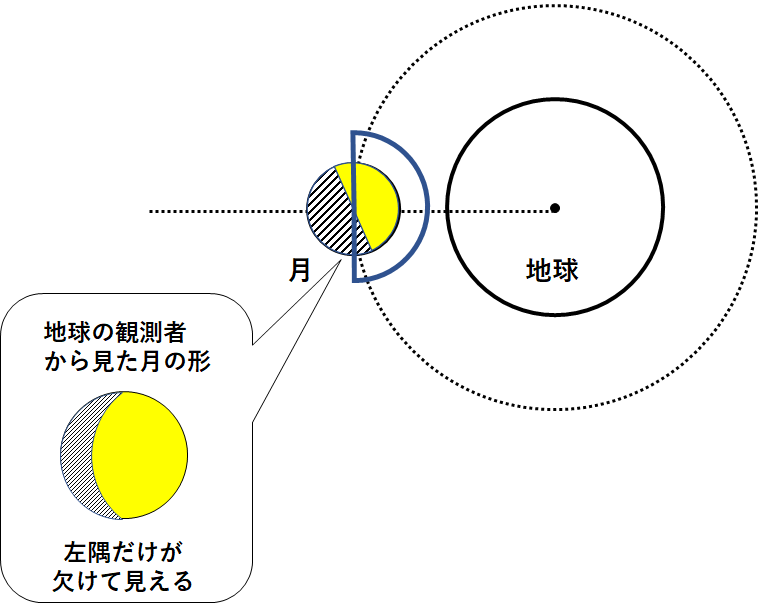
つまり月が地球のまわりを360度公転しても、地球も公転しているので、満月にはなりません。
再び満月になるためにはもう少し日数が必要ということになります。
よって満月から再び満月になるまでには27.3日より長い日数がかかります。(↓の図)
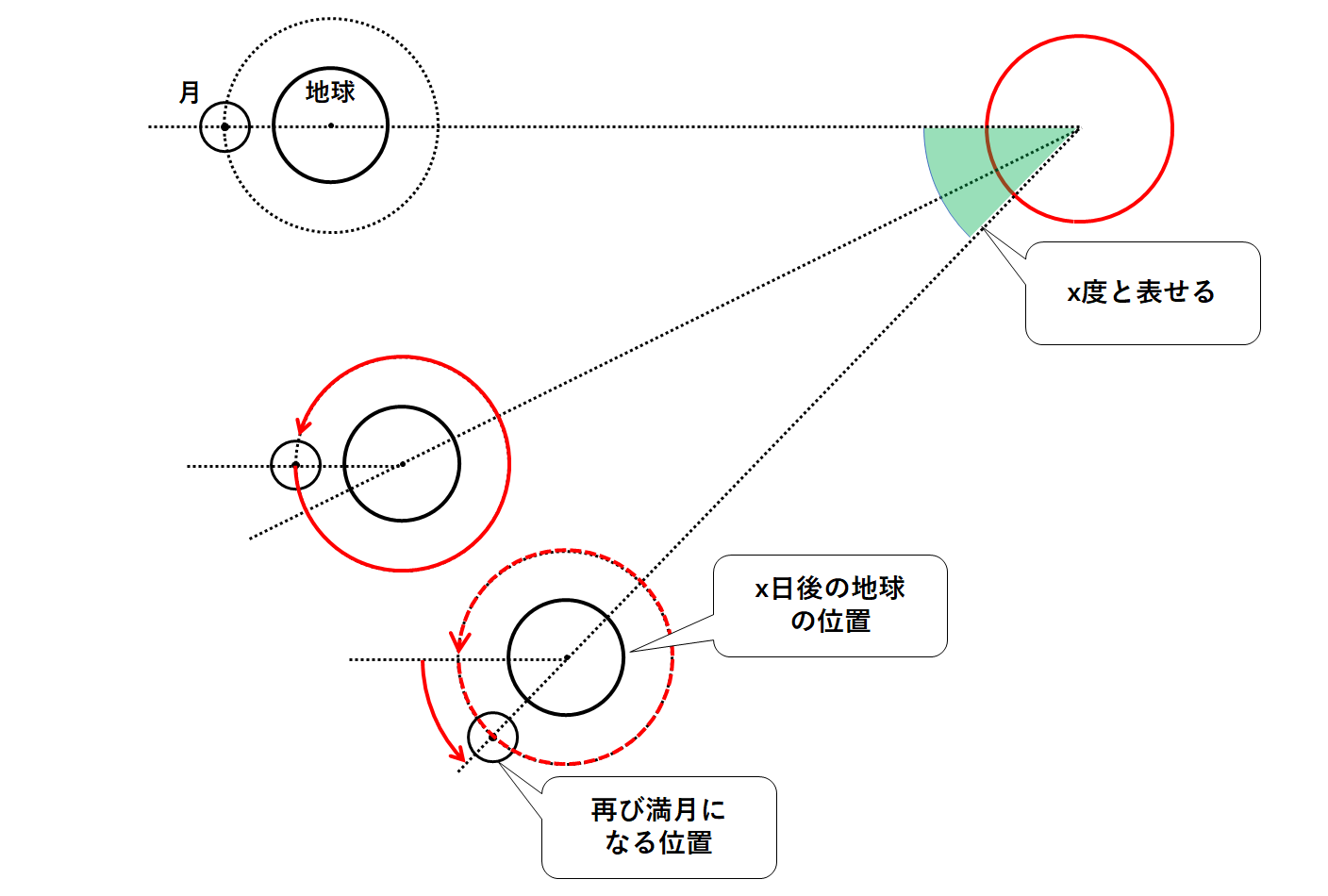
ここではじめの満月が見られた時から再び満月が見られるまでの日数をx日とします。
このときの状況は↓のようになっています。
地球はこのx日でx度公転しています。(↓の図の緑色の角)
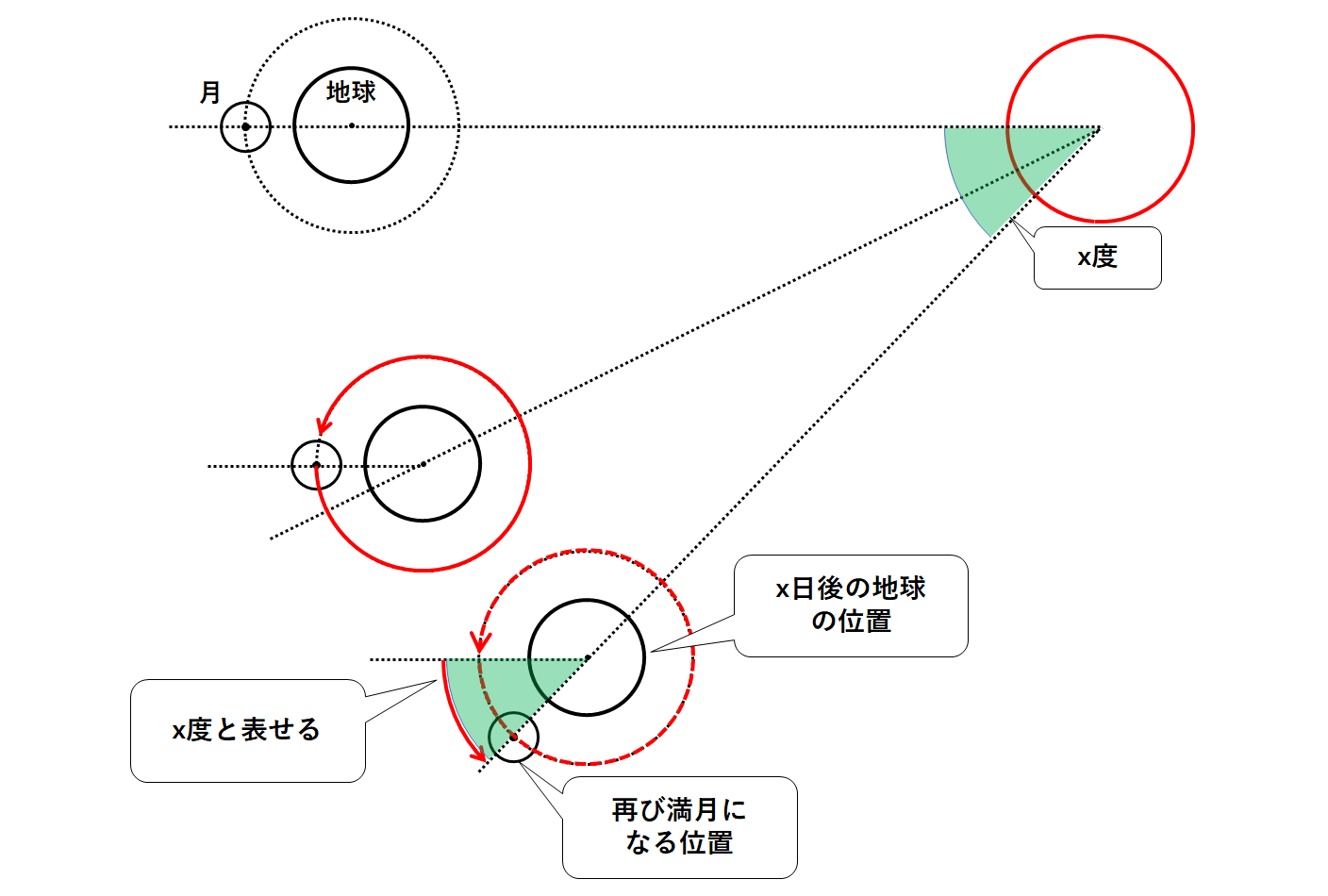
ここで図の緑色の角どうしは平行線における同位角のため等しいです。(↓の図)
このx日で月は 360＋x(度) 公転していることになります。(↓の図)
月の公転周期より27.3日で360度公転するので
$$27.3日：360度＝x(日)：(360＋x)(度) $$
$$360x＝27.3×(360＋x) $$
$$332.7x＝9828$$
$$x＝29.540・・・$$
よってx=約29.5となります。
つまり満月から再び満月になるまでの日数は約29.5日となります。
これを満ち欠けの周期といいます。
■月の満ち欠けの周期
月の公転周期・・・・・・27.3日
月の満ち欠けの周期・・・29.5日
月が公転すると同時に、地球も公転しているため、ずれが生じている。
コメント(承認された場合のみ表示されます)
わかりやすいです！塾の宿題が全然わからなかったので父とやっていたのですが、どちらもわからなっかったのでもめていました。このサイトのおかげで父を説得させることが出来ました。助かりました！
コメントありがとうございます。
参考になり嬉しい限りです。
勉強、がんばってくださいね。
月が360度公転した時→27.3日
ってことはその時地球は27.3度公転している
つまり地球から満月が見えるまで後27.3度
月は一日に何度公転するか計算する→360÷27.3=約13度
さっき地球から満月が見えるまで後27.3度だったから27.3÷13=2.1
つまり地球が公転していなければ後2.1日で満月になる。だが地球は公転している。
だから2.1度地球が公転する。月は1日で13度公転する。後2.1度公転するには2.1÷13=約0.16
ここから細かくなるので誤差だとしてこれまでのかかった日数を計算すると27.3＋2.1＋0.16=29.56日
になるので約29.56日って考えました。中3です。多少誤差はでますけどこの考え方でもいいですか？？
るじゃお様
コメントありがとうございます。
素晴らしい考え方だと思います。
厳密にはるじゃお様のおっしゃる計算をくり返すことでより正確な値が導き出されるはずです。
月の満ち欠けの周期がなぜ約29.5になるのか理解できました。
ありがとうございました！
月曜日ここの単元テストあるので頑張ります😄
るじゃお様
貴重なコメントありがとうございました。
テストもがんばってください。