中1物理【*水圧・浮力・密度の関係】

このページでは「水圧と浮力の関係」「密度と浮力の関係」について紹介しています。

発展的な内容を含みます。

1．水圧と浮力の関係

■水圧

水の重さによる圧力。

次の3点を押さえておこう。

①　水圧の大きさは水面からの深さのみで決まる。

②　水圧の大きさは水深1cmで100Pa。

③　水と接するすべての方向から（物体をつぶす向きに）はたらく。

■浮力

水中にある物体が受ける力。

水圧が原因となってはたらく。

■アルキメデスの原理

水中にある物体が受ける浮力の大きさは、その物体が押しのけた水の重さに等しい。

水中にある物体が受ける浮力の大きさは、その物体が押しのけた水の重さに等しいです。

これをアルキメデスの原理といいます。

しかし本来、浮力というのは水圧が原因となって生じるものです。

ここでは水圧から浮力を計算してみましょう。

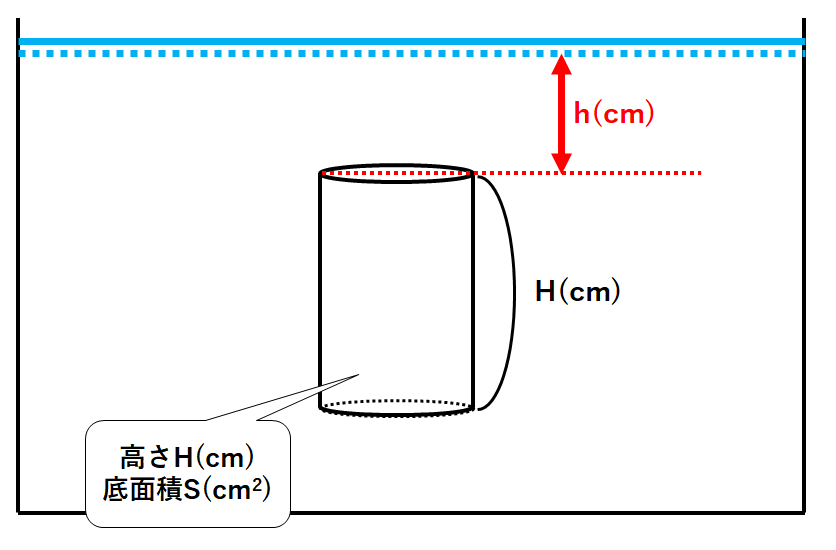
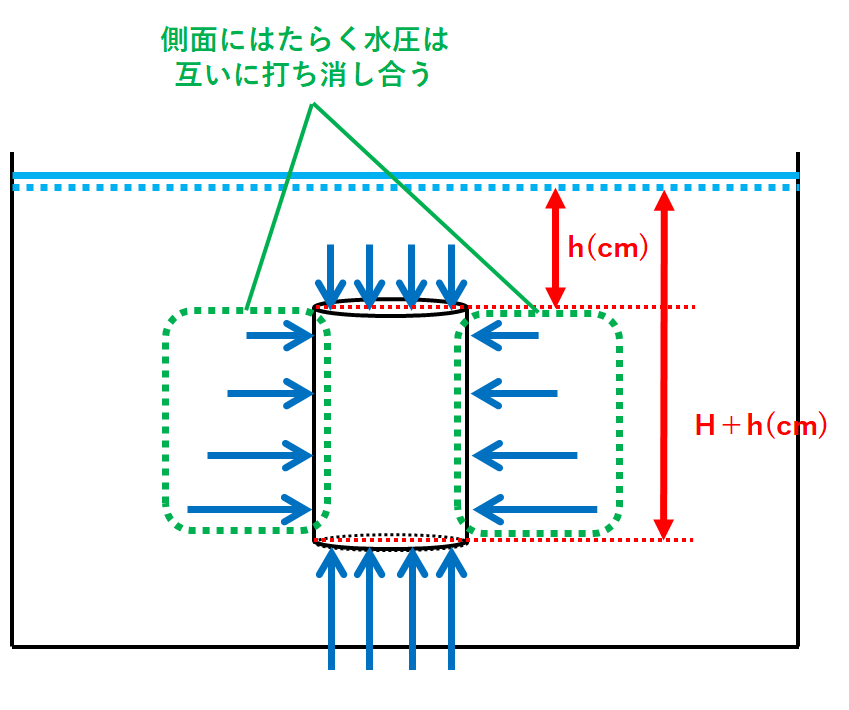
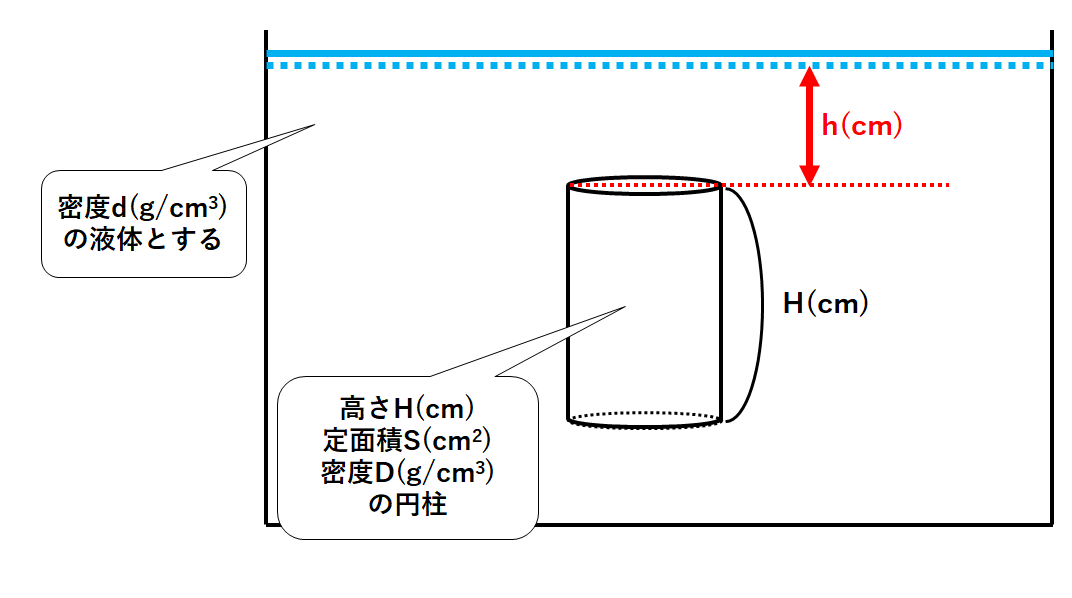
いま↓の図のように容器に水が入っていて

深さh（cm）のところに高さH（cm）・底面積S（cm²）の円柱が沈んでいたとしましょう。

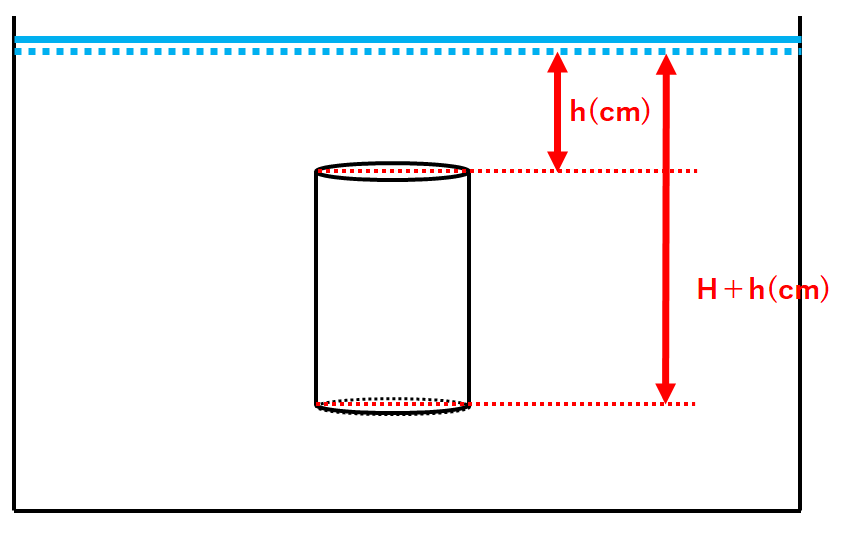
この円柱の上面は深さh（cm）のところにあります。

また円柱の下面は深さH＋h（cm）のところにあります。(↓の図)

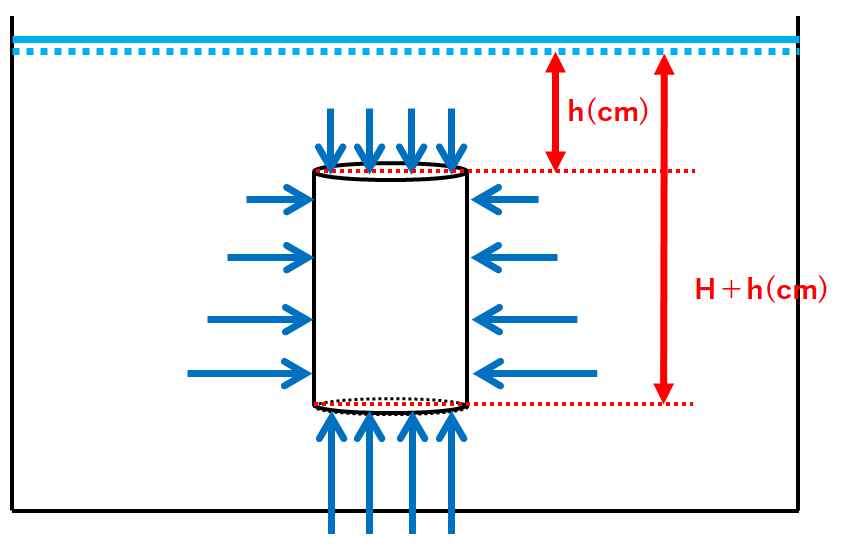
この円柱には水と接するあらゆる方向から水圧が加わっています。（↓の図）

しかし側面の水圧は水深が同じものどうしであればその大きさは等しいため、互いに打ち消し合います。(↓の図)

そのため円柱の上面と下面の水圧のみを考えます。

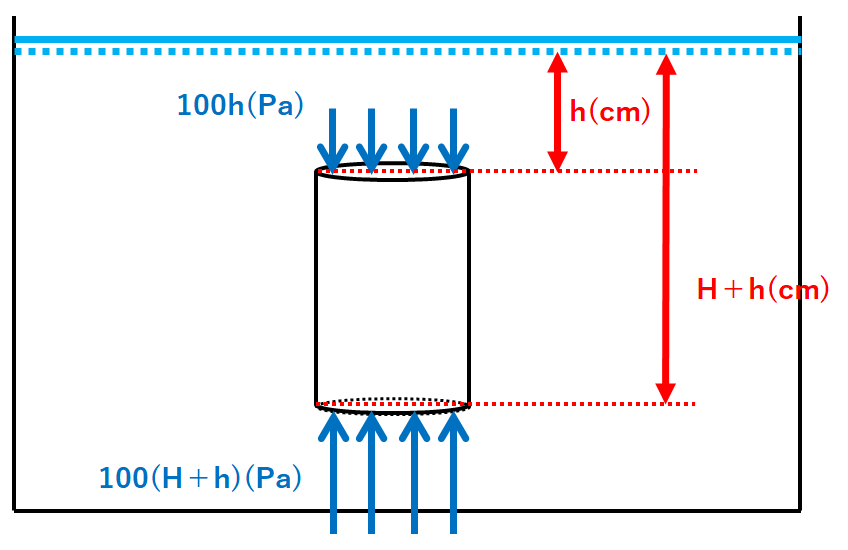
水圧は水深1cmで100Paでした。

上面は深さh（cm）なので、上面にはたらく水圧は

$$100h(Pa)＝100h(N/m^2)$$

下面は深さH＋h(cm)なので、下面にはたらく水圧は

$$100(H＋h)(Pa)＝100(H＋h) (N/m^2)$$

となります。(↓の図)

この水圧によって上面や下面を押す力は

$$力(N)＝圧力(N/m^2)×面積(m^2)$$

で求めることができます。（圧力の公式を変形したもの）

よって

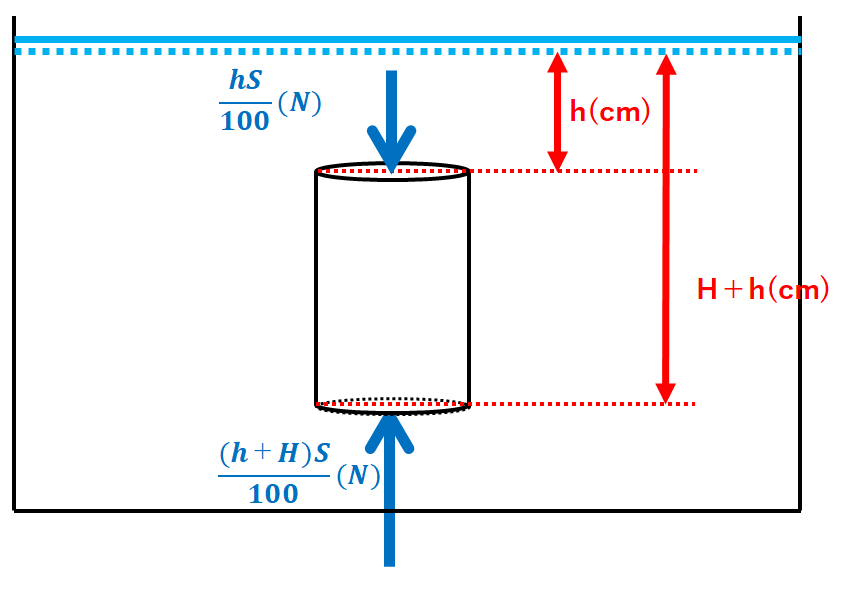
上面にはたらく水圧による力は

$$100h(N/m^2)×\frac{S}{10000}(m^2)＝\frac{hS}{100}(N)$$

下面にはたらく水圧による力は

$$100(H＋h)(N/m^2)×\frac{S}{10000}(m^2)＝\frac{(H＋h)S}{100}(N)$$

となります。(↓の図)

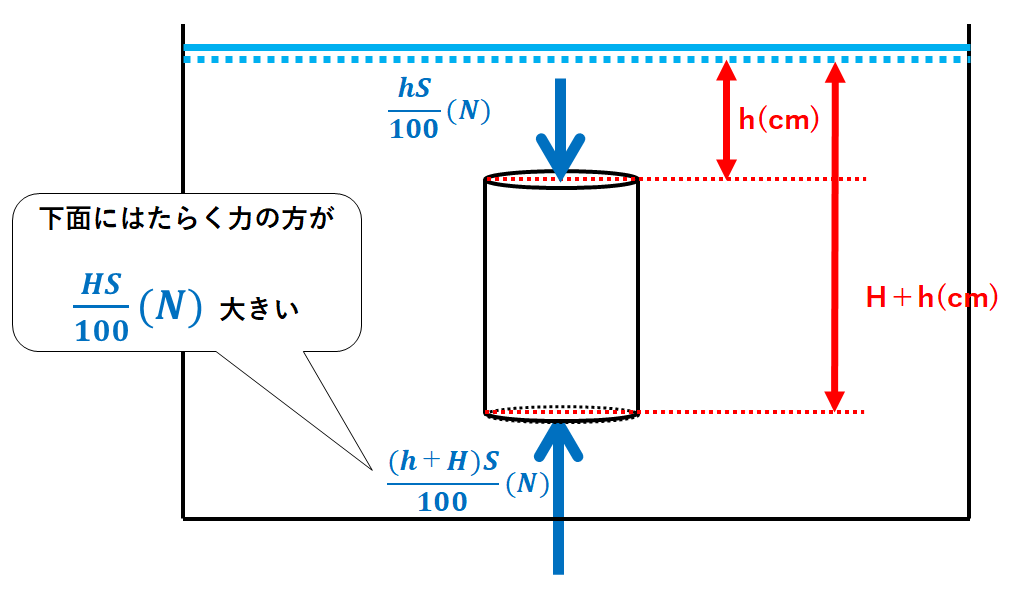
下面にはたらく力の方が大きく、その差は

$$\frac{(H＋h)S}{100}(N)ー\frac{hS}{100}(N)＝\frac{HS}{100}(N)・・・①$$

となります。

これが浮力の大きさです。

一方でアルキメデスの原理から浮力を求めてみましょう。

この円柱の押しのけた水の体積は

$$S(cm^2)×H(cm)＝HS(cm^3)$$

水の密度は1g/cm³なので、押しのけた水の質量は

$$HS(cm^3)×1g/cm^3＝HS(g)$$

100gの物体にはたらく重力を1Nとすると

$$HS(g)　⇒　\frac{HS}{100}(N)・・・②$$

となります。

これが浮力の大きさです。

①・②は全く同じ式です。

実は浮力はこのような2通りの求め方ができます。

このようにして水圧から浮力を求めることもできます。

2．水圧・浮力・密度の関係

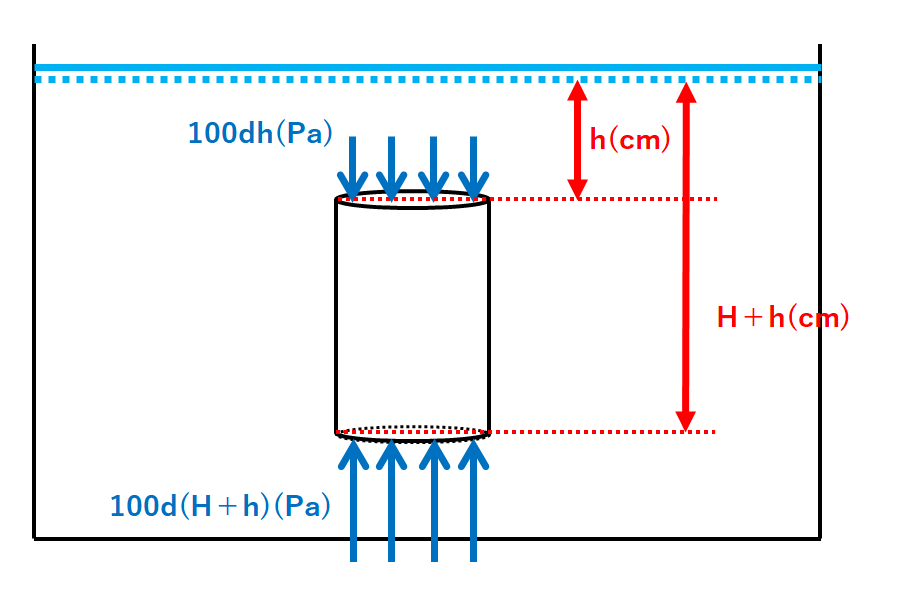
次に密度d（g/cm³）の液体が入った容器に円柱を沈めることを考えます。

沈める円柱は密度D（g/cm³）・高さH（cm）・底面積S（cm²）とします。

下の図のように深さh（cm）のところに沈めたときを考えます。

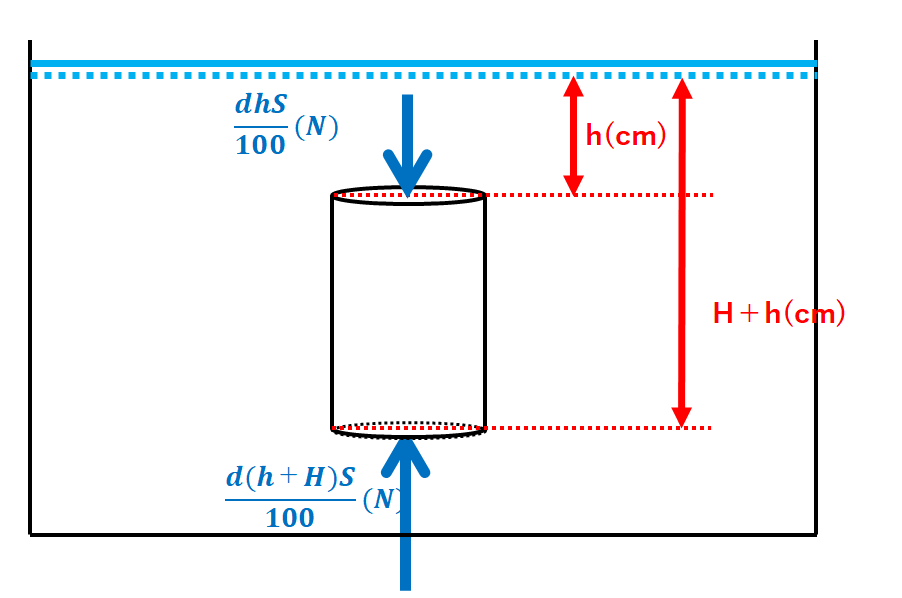
このときの円柱の上面と下面にはたらく液体による圧力を考えます。

水圧は水深1cmで100Paです。

もし密度がd（g/cm³）の液体ならば水深d（cm）で100d（Pa）となります。

円柱の上面は深さh（cm）なので、上面にはたらく水圧は

$$100dh(Pa)＝100dh(N/m^2)$$

円柱の下面は深さH＋h（cm）なので、下面にはたらく水圧は

$$100d(H＋h)(Pa)＝100d(H＋h) (N/m^2)$$

となります。

よって

上面にはたらく液体の圧力による力は

$$100dh(N/m^2)×\frac{S}{10000}(m^2)＝\frac{dhS}{100}(N)$$

下面にはたらく液体の圧力による力は

$$100d(H＋h)(N/m^2)×\frac{S}{10000}(m^2)＝\frac{d(H＋h)S}{100}(N)$$

となります。(↓の図)

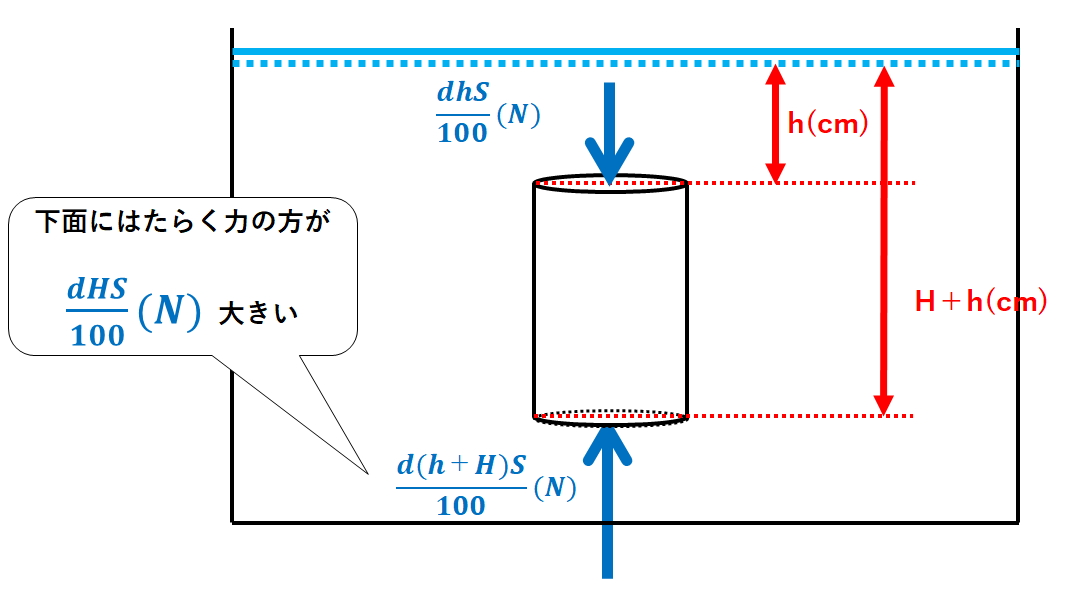
よってこの差は

$$\frac{d(H＋h)S}{100}(N)ー\frac{dhS}{100}(N)＝\frac{dHS}{100}(N)・・・③$$

となります。

これが物体にはたらく浮力です。

一方で円柱にはたらく重力の大きさを考えましょう。

まず円柱の体積は

$$S(cm^2)×H(cm)＝HS(cm^3)$$

円柱の密度はD(g/cm³)なので、その質量は

$$D(g/cm^3)×HS(cm^3)＝DHS(g)$$

これを重さ(N)に直しましょう。

100gの物体にはたらく重力を1Nとすると

$$DHS(g)　⇒　\frac{DHS}{100}(N)・・・④$$

となります。

ここで③(浮力)と④(重さ)を比べてみましょう。

③(浮力)が④(重さ)よりも大きいとき

浮力の方が大きいと円柱は上に動きます。

つまり円柱は液体に浮いてしまうのです。

このとき③＞④なので

$$\frac{dHS}{100}＞\frac{DHS}{100}$$

よって

d＞D

です。

d＞Dならば円柱は浮いてしまうということです。

④(重さ)が③(浮力)よりも大きいとき

重力の方が大きいと円柱は下に動きます。

つまり円柱は液体に沈んでしまうのです。

このとき③＜④なので

$$\frac{dHS}{100}＜\frac{DHS}{100}$$

よって

d＜D

です。

d＜Dならば円柱は沈んでしまうということです。

これらは→【密度】←の単元にもあるように

物体が液体に浮く・・・物体の密度が液体よりも小さい

物体が液体に沈む・・・物体の密度が液体よりも大きい

ということを示していることになります。

浮く・沈むは元をただせば浮力や水圧から来ているということです。