中3物理【*連結された物体の運動】

1．*連結された物体の運動

物体Aと物体Bが質量の無視できる糸によってつながれています。
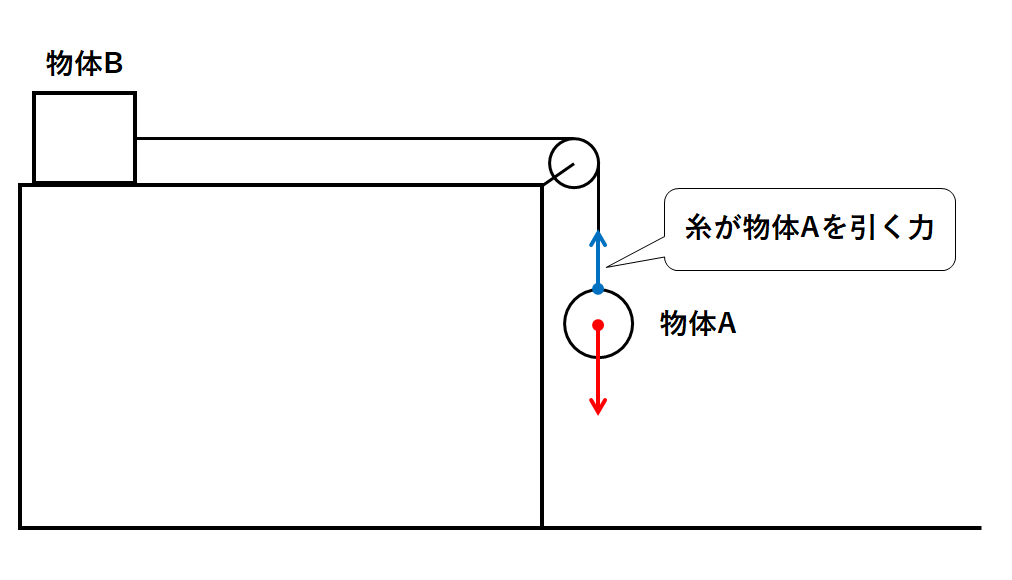
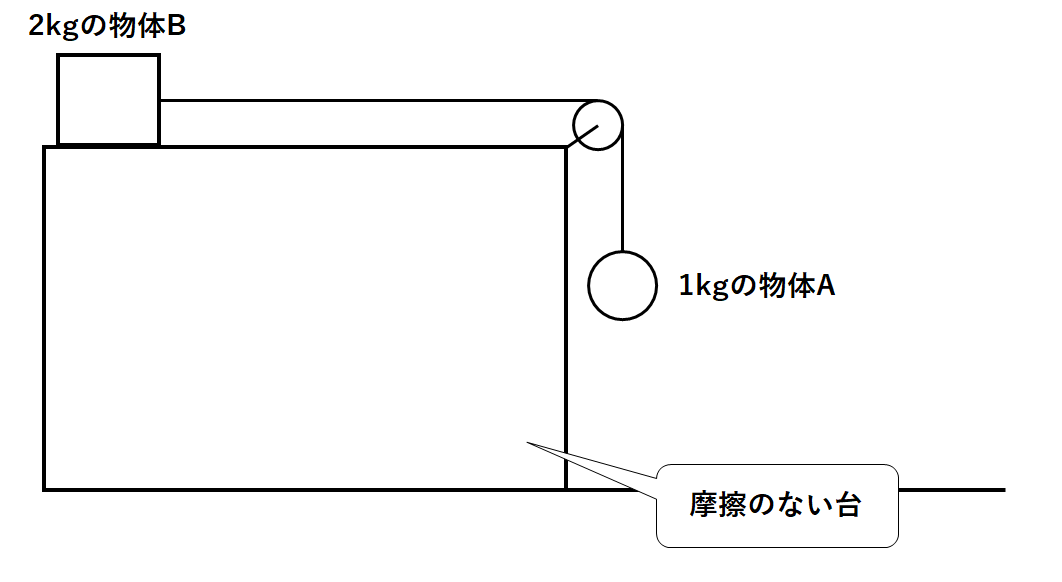
これを↓の図のように、滑車のついた摩擦のない台に置いたとします。

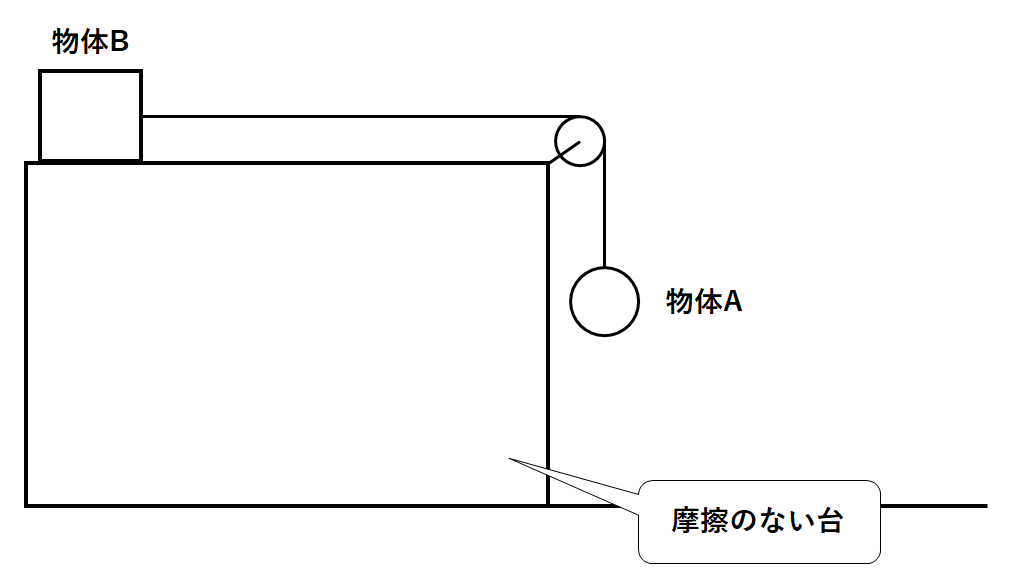
ここで静かに手を放すと物体A・物体Bは動き出します。
この運動について考えましょう。

ざっくり考えてみると、
物体Aは自由落下に近いような運動をします。
物体Bは糸で物体Aとつながっているので(向きは違いますが)Aと同じ速さで右向きに運動します。
(物体Aと物体Bは連動して動き、その速さは同じということ)

もう少し詳しく考えます。
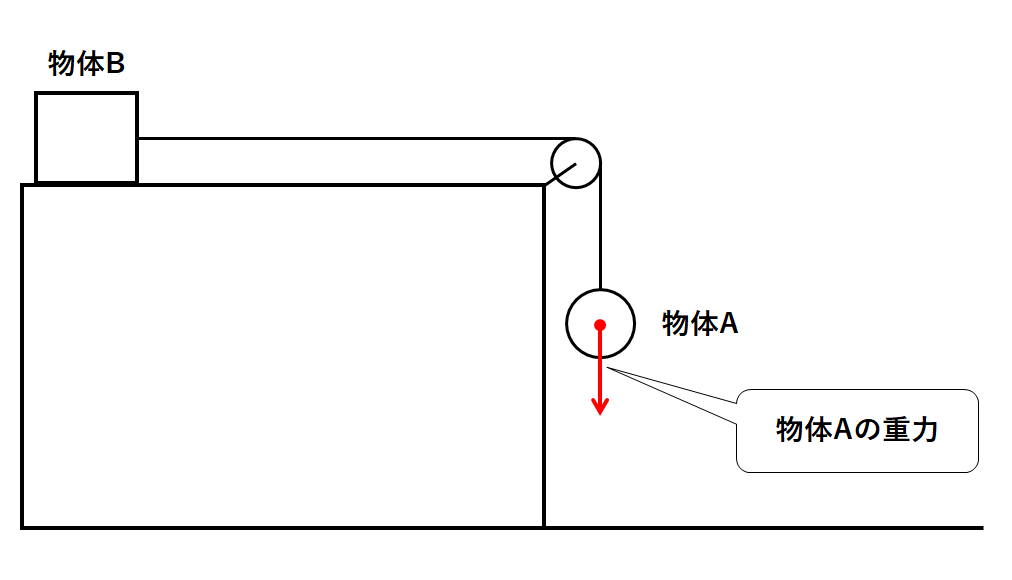
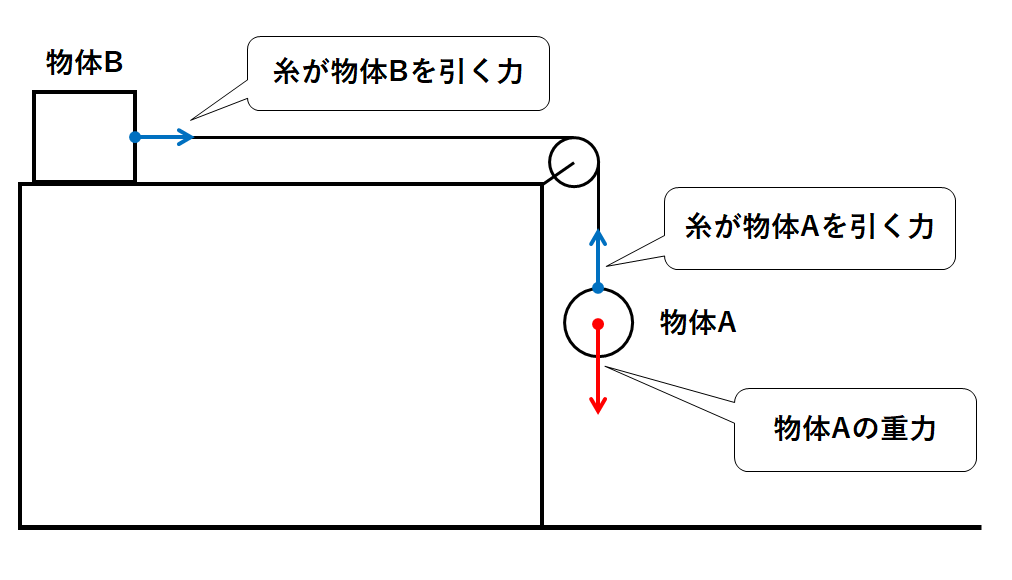
まず物体Aには重力がはたらいています。(↓の図)

一方で糸が物体Aを引く力も存在します。(↓の図)

全体としては物体Aには下向きの力がはたらいていることになるので、物体Aは落下します。
(物体Aの重力＞糸が物体Aをひく力　となっている)

このとき物体Aには一定の大きさの力(＝物体Aの重力－糸が物体Aをひく力)がはたらき続けています。
よって、物体Aは一定の割合で速さが増加していきます。(等加速度直線運動)

物体Bには、糸がAを引く力によって生じた糸がBを引く力がはたらいています。(↓の図)

つまり物体Bにも一定の大きさの力がはたらき続けています。
そのため、物体Bも一定の割合で速さが増加していきます。(等加速度直線運動)

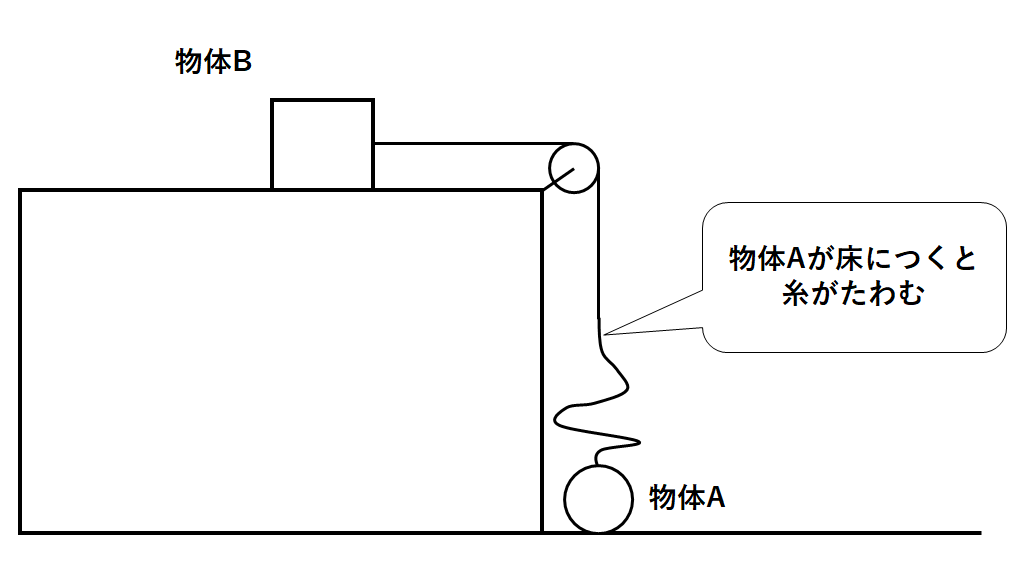
いずれ物体Aは床について、糸がたわんでしまいます。(↓の図)

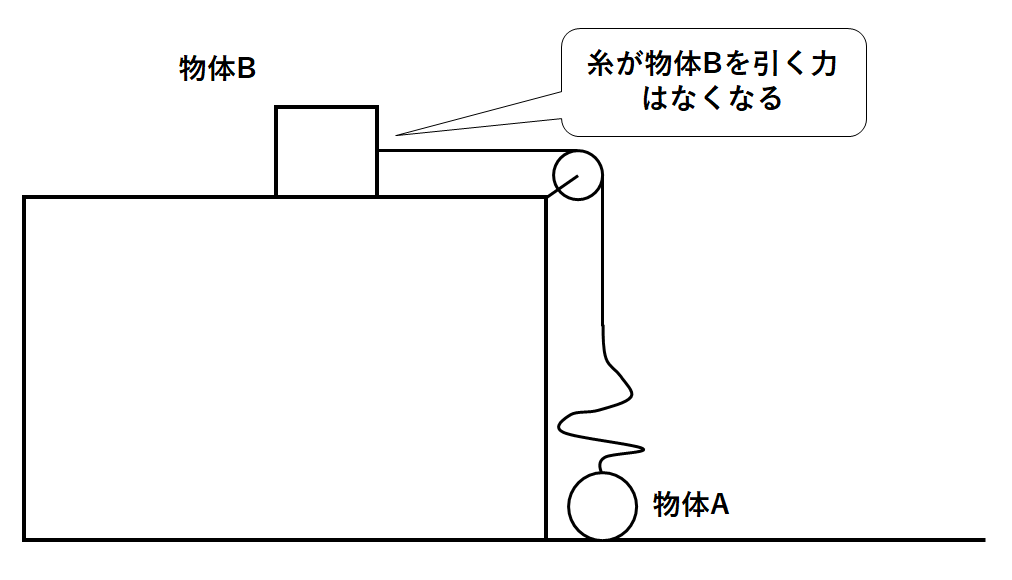
すると糸が物体Bを引く力というのはなくなってしまいます。(↓の図)

物体Bに運動方向にはたらく力がなくなるので、物体Bは等速直線運動をします。
(もし摩擦があれば速さが減少します。)

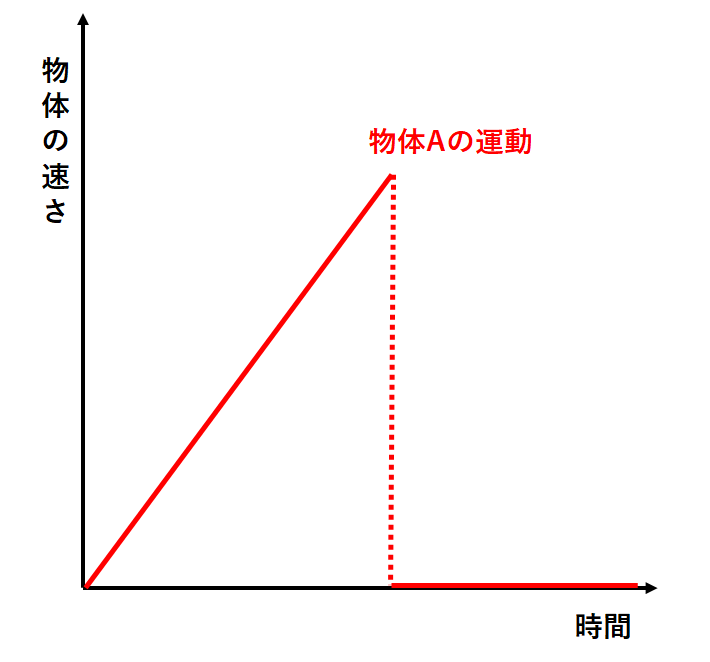
A・Bの運動のようすを横軸：時間　縦軸：速さのグラフにとると

物体Aのグラフは↓のように

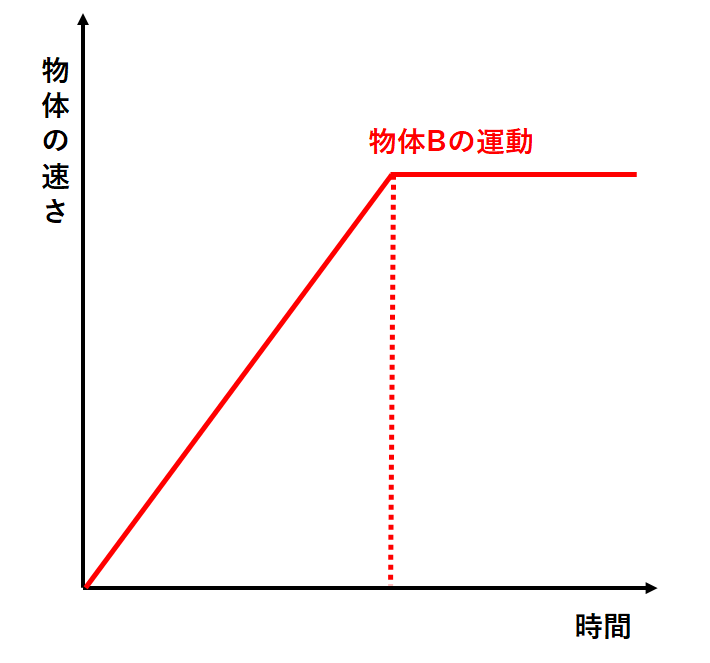
物体Bのグラフは↓のように

なります。

2．*連結された物体の力学的エネルギー

1kgの物体Aと2kgの物体Bが質量の無視できる糸によってつながれています。
先ほどと同様に、これを↓の図のように、滑車のついた摩擦のない台に置いたとします。

ここで物体Aが6m落下したときの物体Aの運動エネルギー・物体Bの運動エネルギーを考えます。
(6m落下しても物体Aは床につかない・物体Bは台の上を運動中とします。)

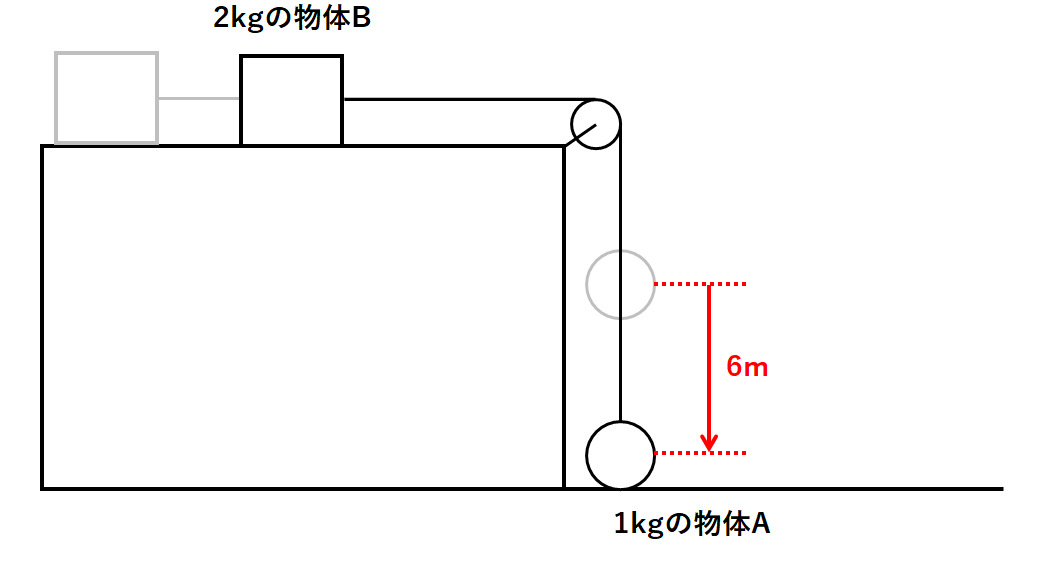
また以下では1kgの物体にはたらく重力は10Nであるとし、空気抵抗も考えないものとします。

この例のような連結された物体の力学的エネルギーは
物体Aの力学的エネルギー＋物体Bの力学的エネルギーが保存されます。

言い方を変えると
連動して動く物体Aと物体Bを1つの物体としてみなし、
この物体の力学的エネルギーが保存される
という考え方です。

物体Aだけの力学的エネルギーは保存されないし、物体Bだけの力学的エネルギーも保存されない、ということなんですね。
ここの考え方、結構重要です。

では、物体Aが6m落下したときの物体Aの運動エネルギー・物体Bの運動エネルギーを求めましょう。

まず
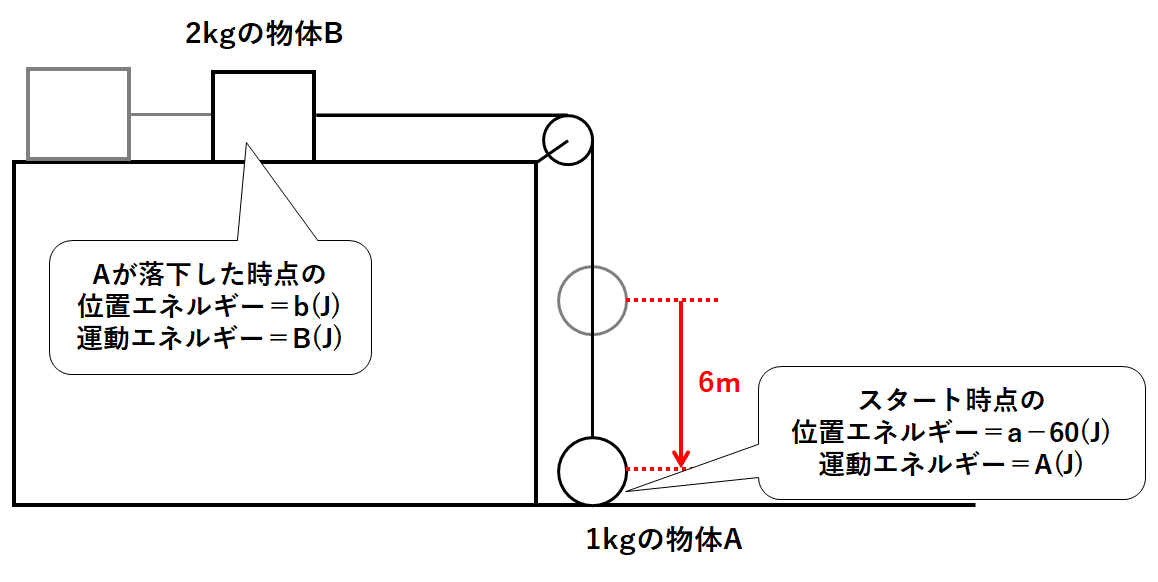
物体Aがスタートする時点での物体Aの位置エネルギーをa(J)・物体Bの運動エネルギーをb(J)とします。
物体Aが6m落下した時点での物体Aの運動エネルギーをA(J)・物体Bの運動エネルギーをB(J)とします。
です。

次に
物体Aの位置エネルギーが減少しています。その値は、
$$10N×6m=60J$$

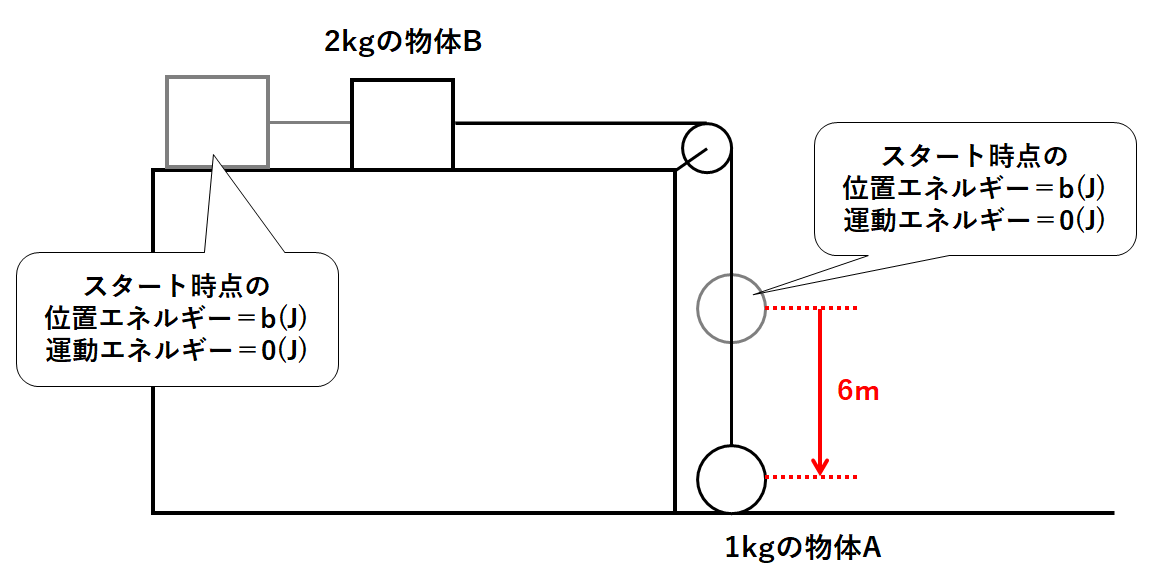
ここで物体Aがスタートする時点で

$$物体Aの位置エネルギー=a(J) $$
$$物体Aの運動エネルギー=0J$$
$$物体Bの位置エネルギー=b(J) $$
$$物体Bの運動エネルギー=0(J) $$
合わせると
$$連結物体の力学的エネルギー=a+b(J)・・・①$$
です。

そして物体Aが6m落下した時点で

$$物体Aの位置エネルギー=a-60(J) $$
$$物体Aの運動エネルギー=A(J) $$
$$物体Bの位置エネルギー=b(J) $$
$$物体Bの運動エネルギー=B(J) $$
合わせると
$$連結物体の力学的エネルギー=a+b+A+B-60(J)・・・②$$

力学的エネルギーの保存より、①と②は等しいので
$$a+b=a+b+A+B-60$$
よって
$$A+B=60J・・・③$$
となります。

ここで運動エネルギーは
$$\frac{1}{2}×質量×速さ^2$$
で求められたので
$$A:B=\frac{1}{2}×1kg×速さ^2: \frac{1}{2}×2kg×速さ^2$$

物体A・Bともに速さは等しいので
$$A:B=1:2・・・④$$
となります。

③④より
$$A=20J 　　B=40J$$
となります。

このように連結物体どうしの運動エネルギーは質量比によって決まります。
(速さが同じであるため、運動エネルギーのちがいは質量のちがいによって決まる)

これがわかっていれば、文字式を使わず解くこともできます。
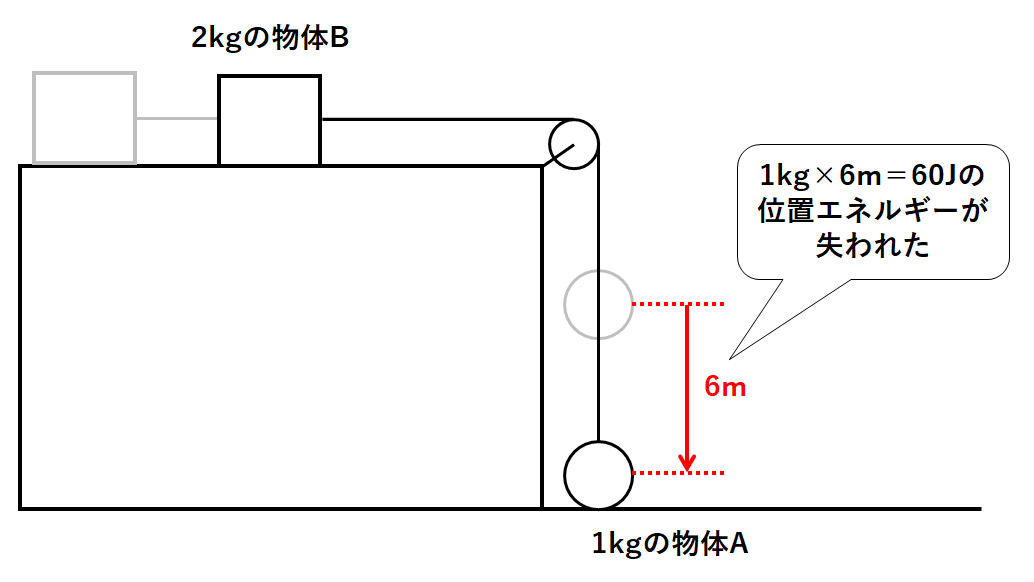
このAとBの連結物体は60Jの位置エネルギーを失いました。(↓の図)

それ以外に失われたエネルギーはありません。

ということはこの60Jは運動エネルギーへと移り変わるはずです。

つまり
$$Aの運動エネルギー+Bの運動エネルギー=60J$$
ということになり
$$Aの運動エネルギー:Bの運動エネルギー=1:2$$
であるので
$$A=20J 　　B=40J$$
となります。

POINT!
連結物体の運動は・・・
・連動して動く物体どうしを1つの物体としてみなし、この物体の力学的エネルギーが保存されると考える。
・連結物体どうしの運動エネルギーは質量比によって決まる。