中3物理【分力を使った力のつり合い】

力の合成・分解を利用して3力のつり合いを考えてみましょう。

力の合成・分解に関しては→【力の合成・分解】←を参考に。
また三平方の定理に関する知識も必要です。

分力を使った力のつり合い

例題1

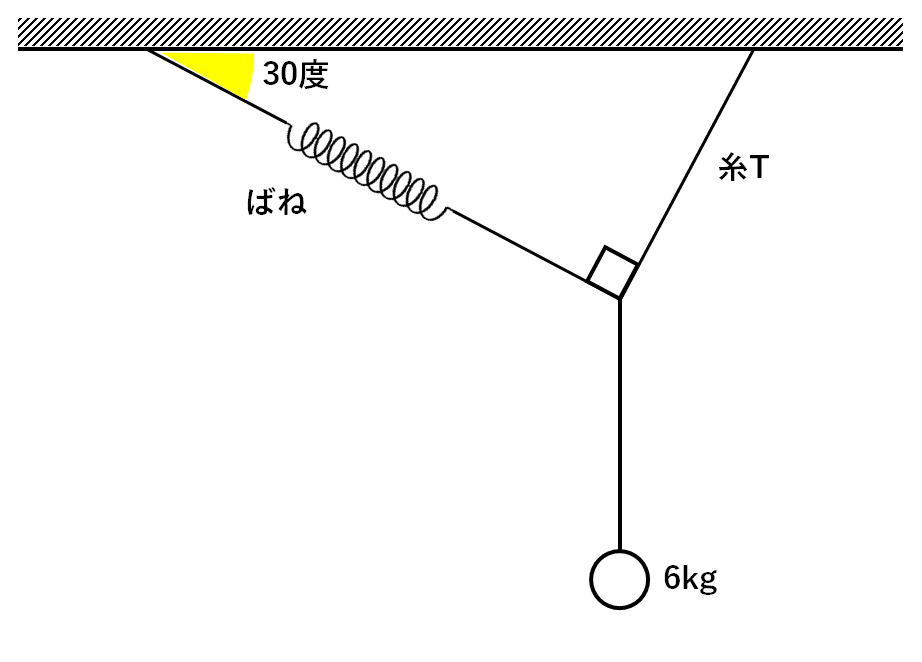
ばねと糸、6kgのおもりを次のようにつなぐと、図の状態で静止した。
このときばね・糸Tに加わる力はそれぞれ何Nか。
ただし100gの物体にはたらく重力を1Nとする。

解法①　糸・ばねの方向に力を分解する

おもりの質量は6kgです。
このおもりには60Nの重力がはたらいています。
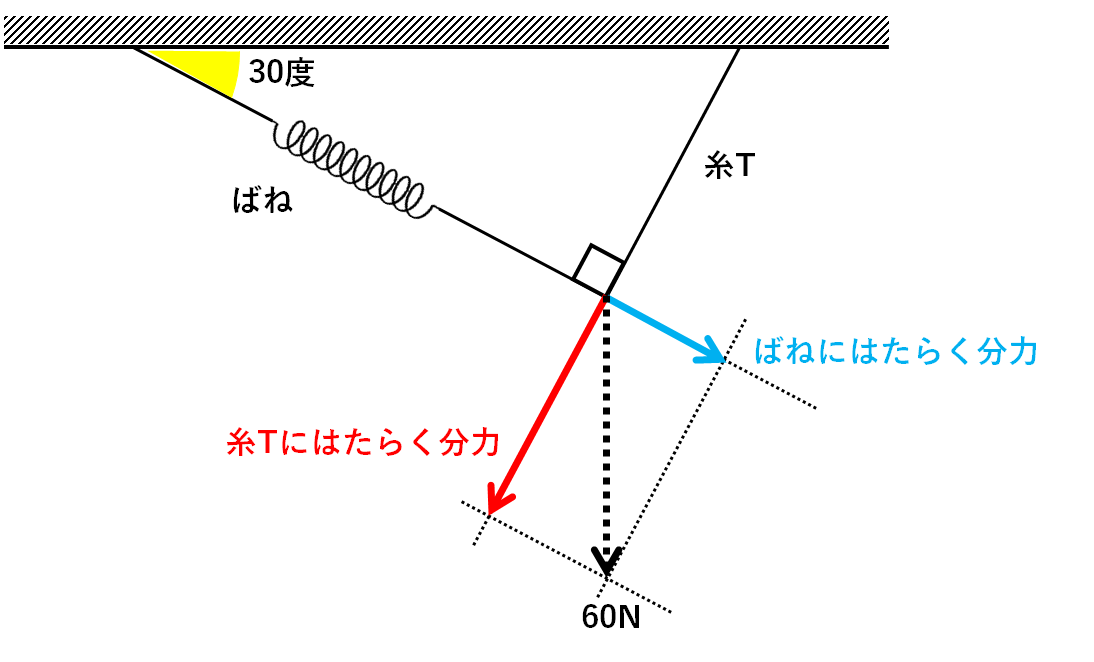
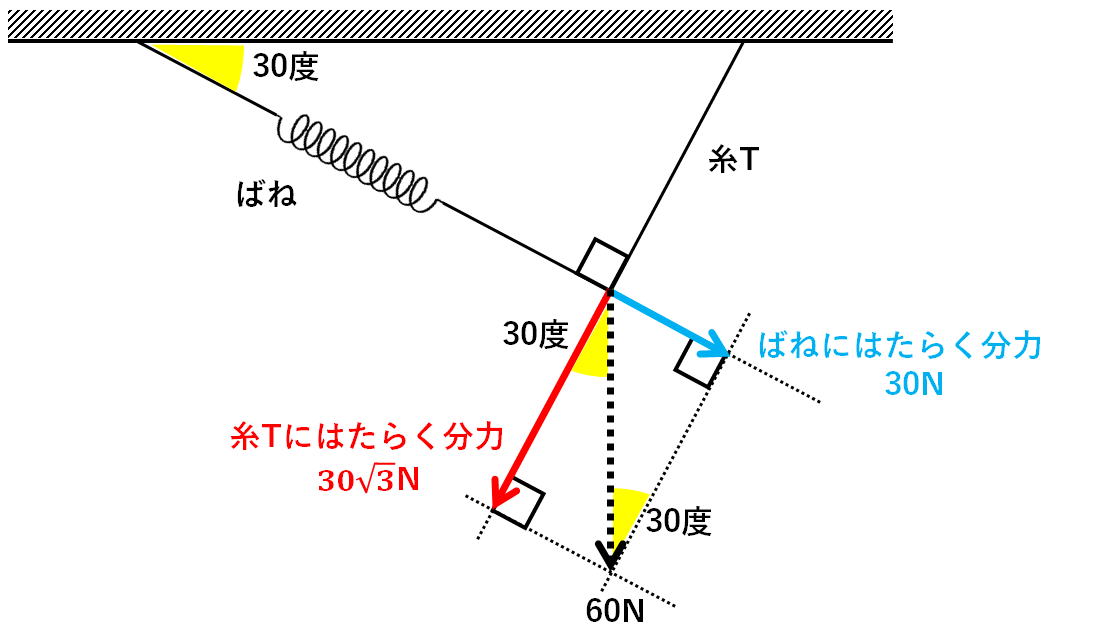
この力を↓の図のように糸Tの延長方向・ばねの延長方向に分解することを考えます。

※作図手順は→【力の合成・分解】←を参考に。

手順に沿って作図すると↓のようになります。

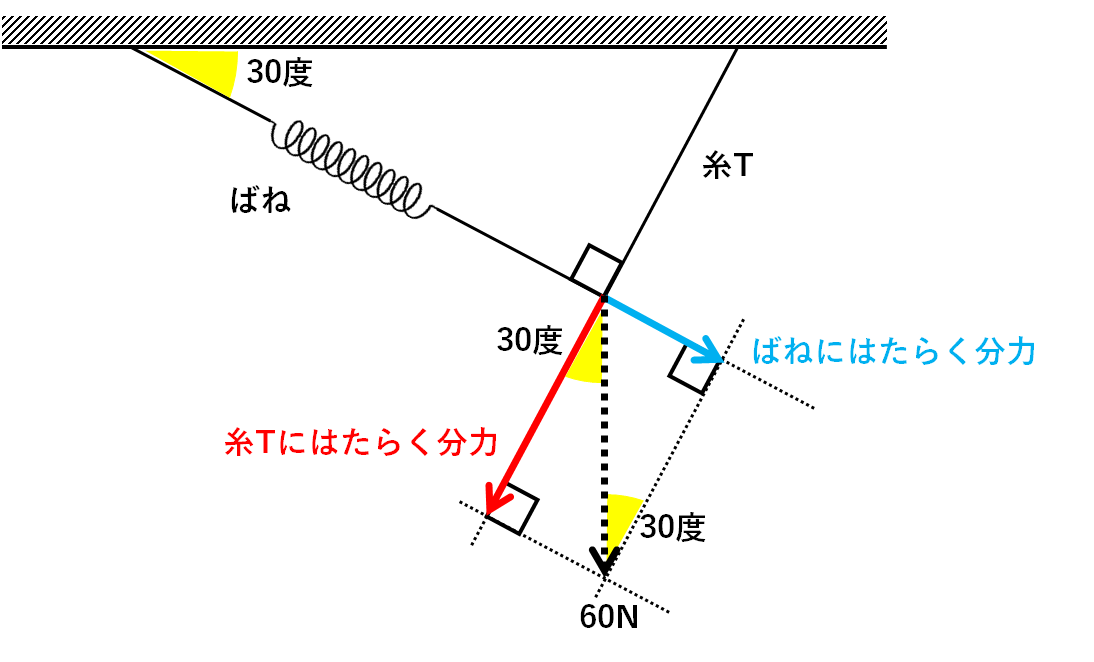
このときできた三角形に注目すると・・・
30度・60度・90度の三角形が隠れています。(↓の図)

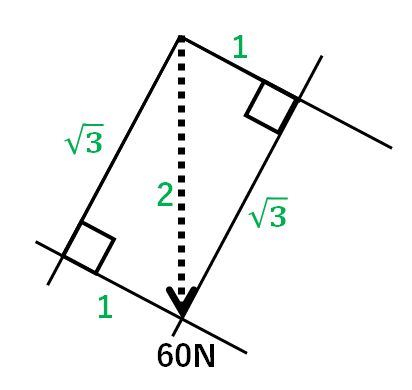
この三角形の辺の比は
$$1:\sqrt{3}:2$$
です。(↓の図)

よって
$$糸Tにはたらく分力=60N×\frac{\sqrt{3}}{2}=30\sqrt{3}(N)$$

$$ばねにはたらく分力=60N×\frac{1}{2}=30(N)$$
となります。(↓の図)

解法②　張力や弾性力を水平・鉛直方向に分解

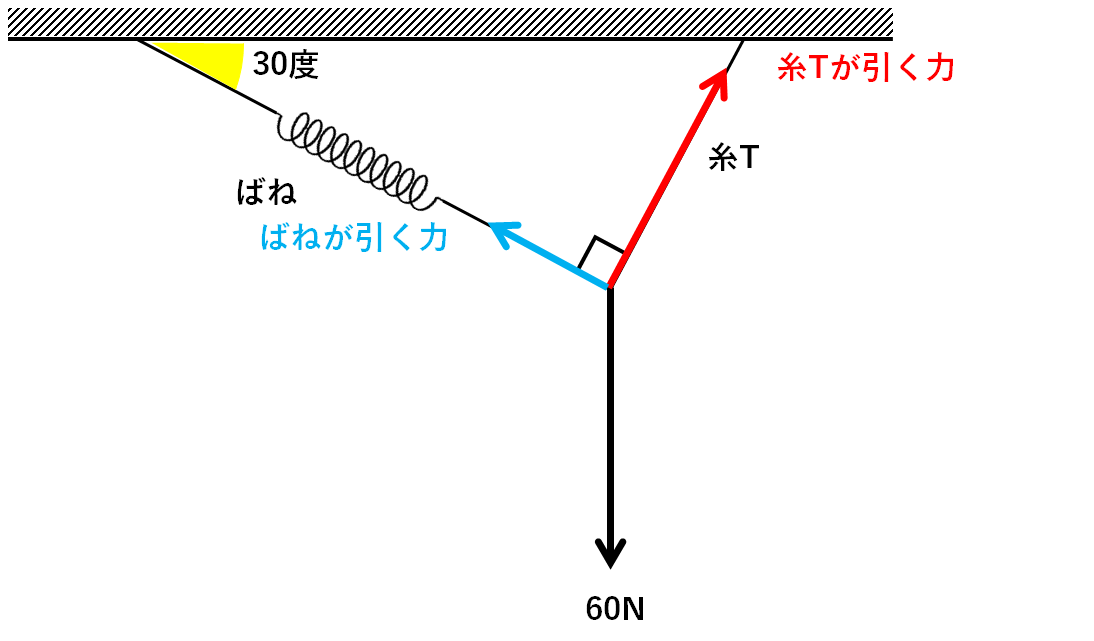
張力とは糸が物体を引く力です。
また、
弾性力とはばねが物体を引く力です。

それぞれを図示すると↓のようになります。

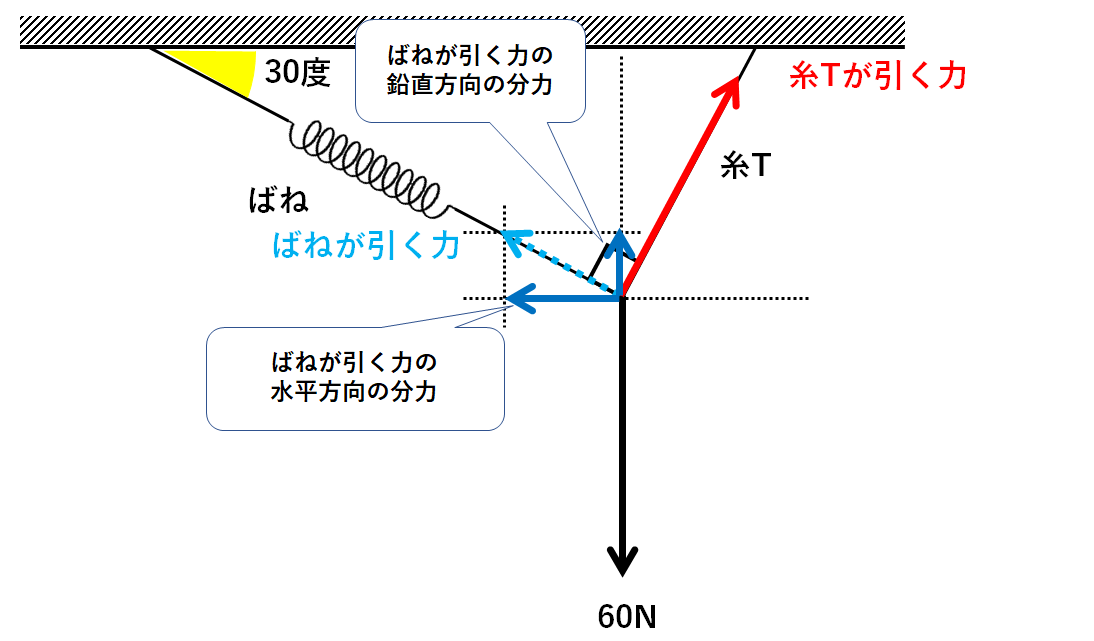
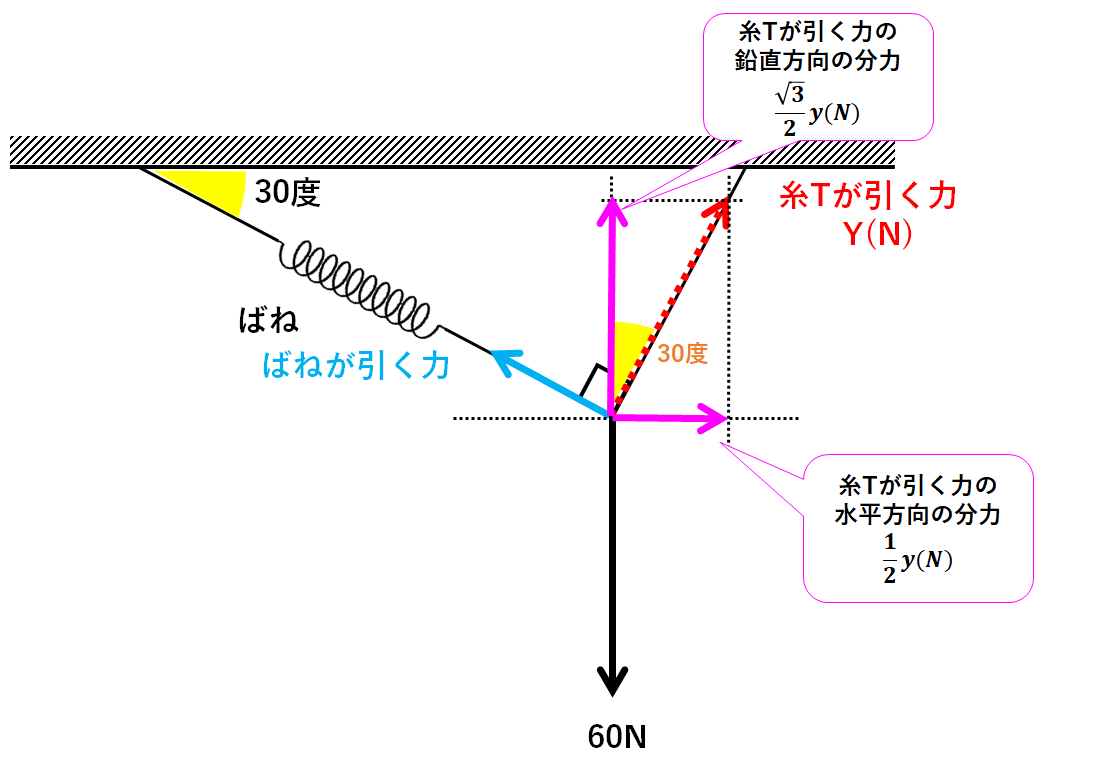
これを水平・鉛直方向に分解します。(↓の図)
(水平・・・横方向　　鉛直・・・縦方向)

まずはばねが引く力を分解しましょう。(↓の図)

ここにも30度・60度・90度の三角形がかくれています。

ばねが引く力をx(N)とすると

$$ばねが引く力の水平方向の分力=x(N)×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}x(N)$$

$$ばねが引く力の鉛直方向の分力=x(N)×\frac{1}{2}=\frac{1}{2}x(N)$$
と表せます。(↓の図)

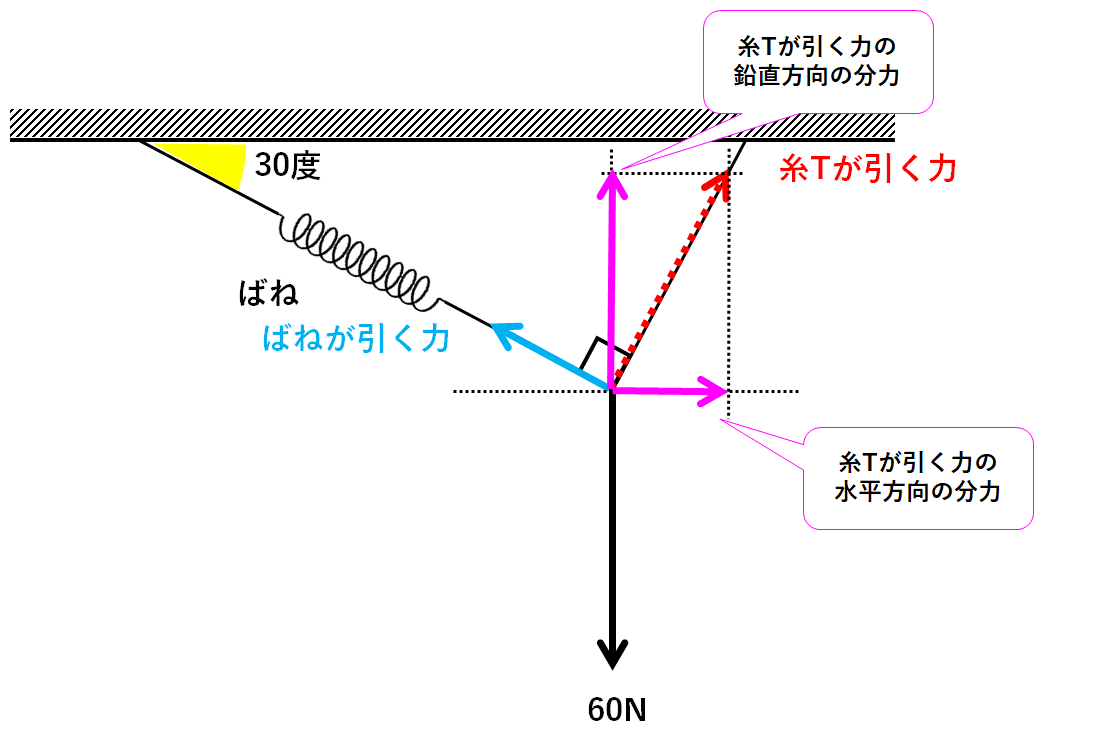
続いて糸Tが引く力を分解しましょう。

またも30度・60度・90度の三角形がかくれています。

糸Tが引く力をy(N)とすると

$$糸Tが引く力の水平方向の分力=y(N)×\frac{1}{2}=\frac{1}{2}y(N)$$

$$糸Tが引く力の鉛直方向の分力=y(N)×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}y(N)$$

と表せます。(↓の図)

まとめると↓の図のようになります。

ここで
水平方向の力がそれぞれつり合い、鉛直方向の力もそれぞれつりあっているはず。

水平方向の力のつり合いから
$$\frac{\sqrt{3}}{2}x(N)=\frac{1}{2}y(N)・・・①$$

鉛直方向の力のつり合いから
$$\frac{1}{2}x(N)+\frac{\sqrt{3}}{2}y(N)=60(N)・・・②$$

①・②をx・yに関する連立方程式として解くと
$$x=30(N)$$

$$y=30\sqrt{3}(N)$$

となります。

よって
$$糸Tにはたらく分力=30\sqrt{3}(N)$$
$$ばねにはたらく分力=30(N)$$
となります。

例題2

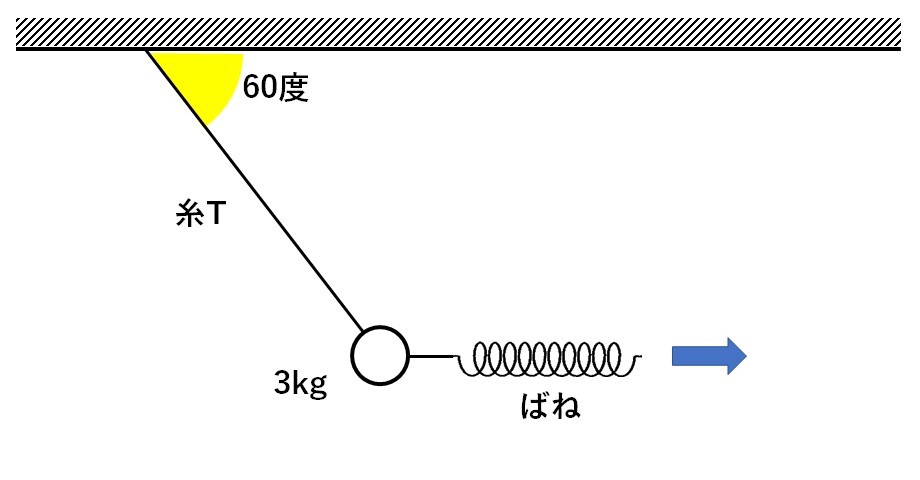
糸T・ばね・3kgのおもりを使って
↓の図のようにばねを右向きに引っ張って静止させた。
このときばね・糸Tに加わる力はそれぞれ何Nか。
ただし100gの物体にはたらく重力を1Nとする。

解法①　糸・ばねの方向に力を分解する

おもりの質量は3kgです。
このおもりには30Nの重力がはたらいています。

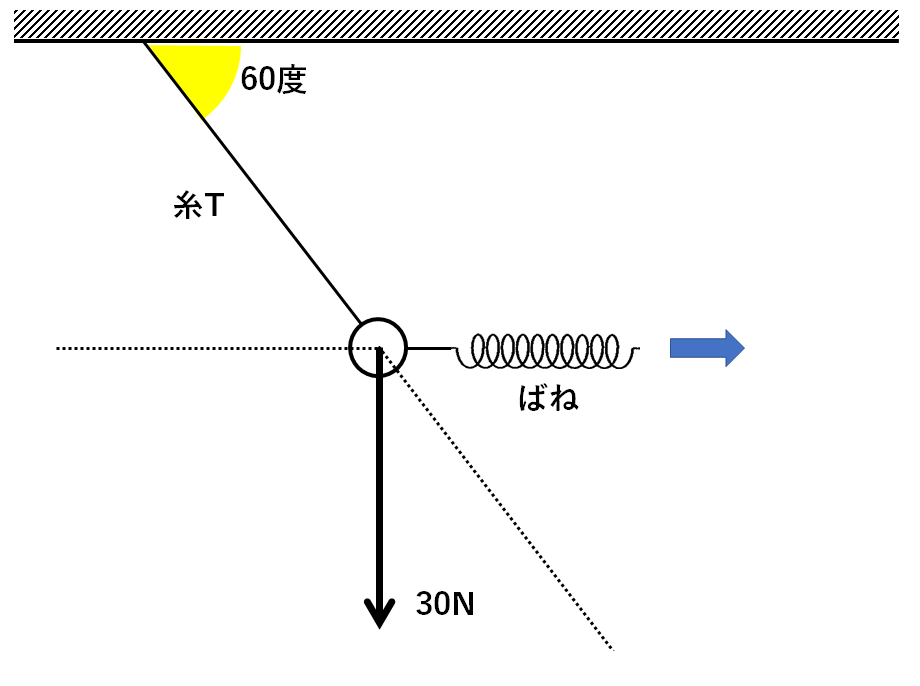
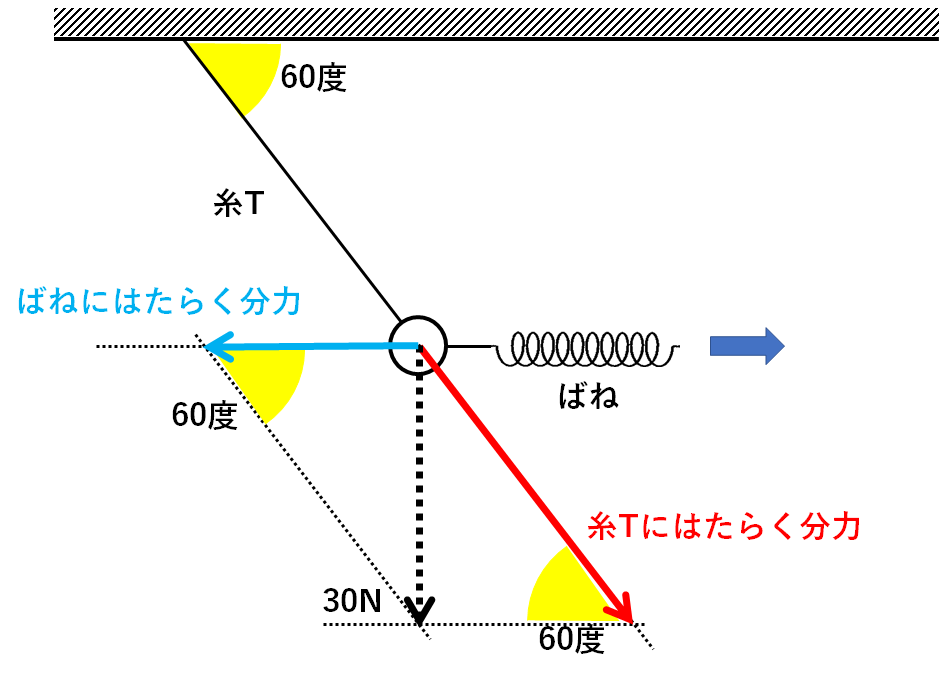
この力を↓の図のように糸Tの延長方向・ばねの延長方向に分解することを考えます。

これを分解すると↓の図のようになります。

このときできた三角形に注目すると・・・

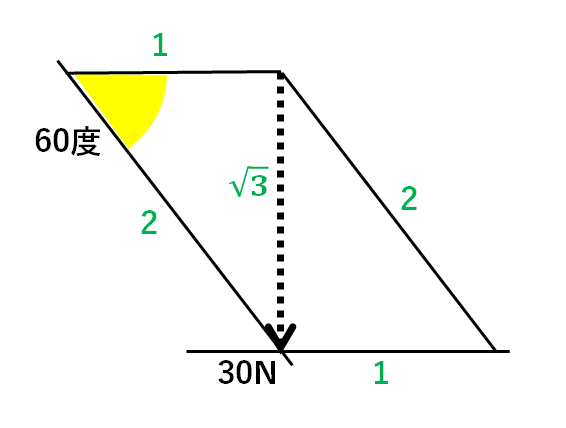
やっぱり30度・60度・90度の三角形が隠れています。(↓の図)

この三角形の辺の比は
$$1:\sqrt{3}:2$$
です。(↓の図)

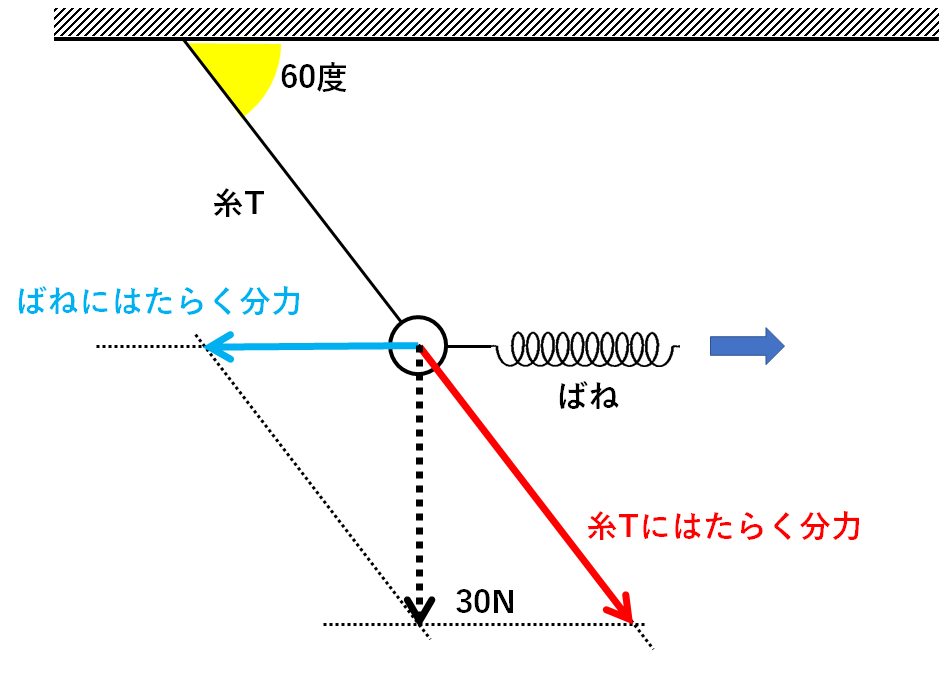
よって

$$ばねにはたらく分力=30N×\frac{1}{\sqrt{3}}=\frac{30}{\sqrt{3}}(N)$$

$$糸Tにはたらく分力=30N×\frac{2}{\sqrt{3}}=\frac{60}{\sqrt{3}}(N)$$

となります。(↓の図)

有理化すると
$$ばねにはたらく分力=10\sqrt{3}(N)$$

$$糸Tにはたらく分力=20\sqrt{3}(N)$$
です。

解法②　張力や弾性力を水平・鉛直方向に分解

例題1の解法②でも書いた通り
張力とは糸が物体を引く力です。
弾性力とはばねが物体を引く力です。

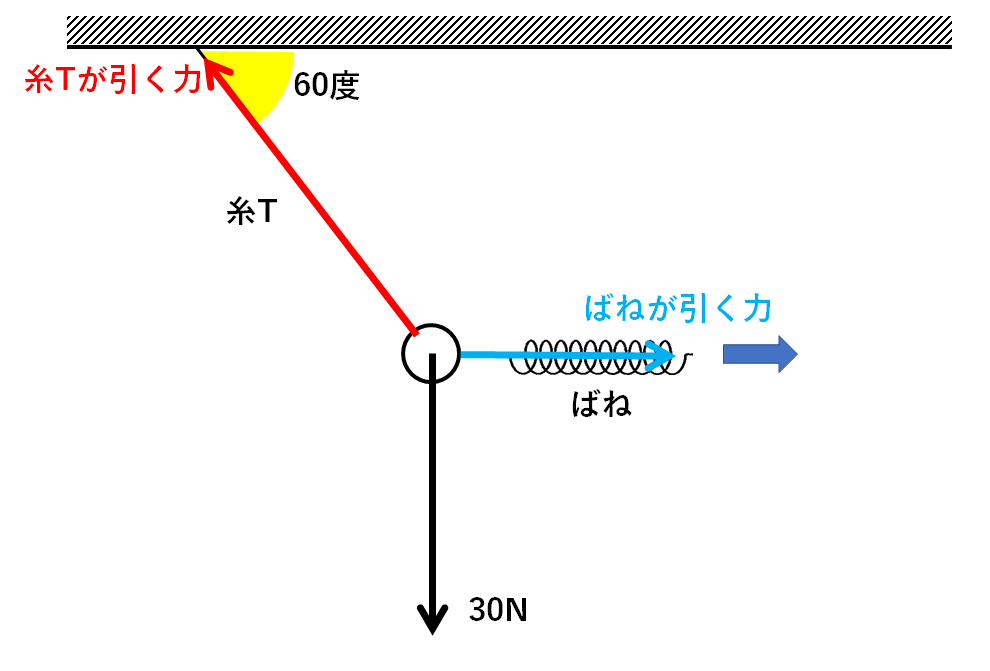
それぞれを図示すると↓のようになります。

これを水平・鉛直方向に分解します。(↓の図)
(水平・・・横方向　　鉛直・・・縦方向　)

ばねが引く力は水平方向の力なので分解はできません。
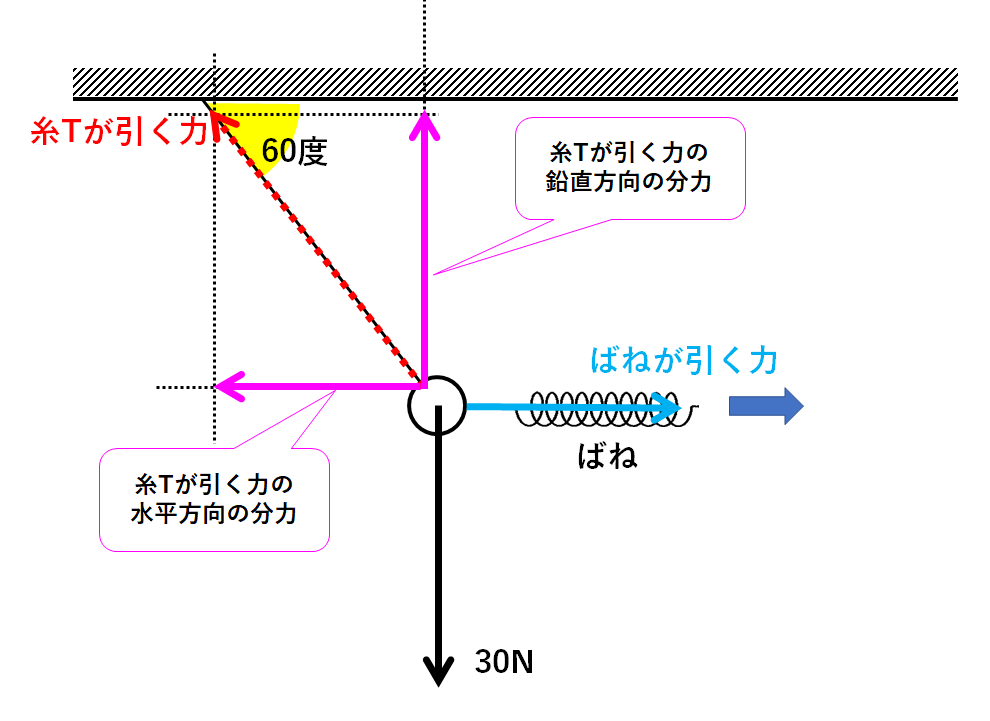
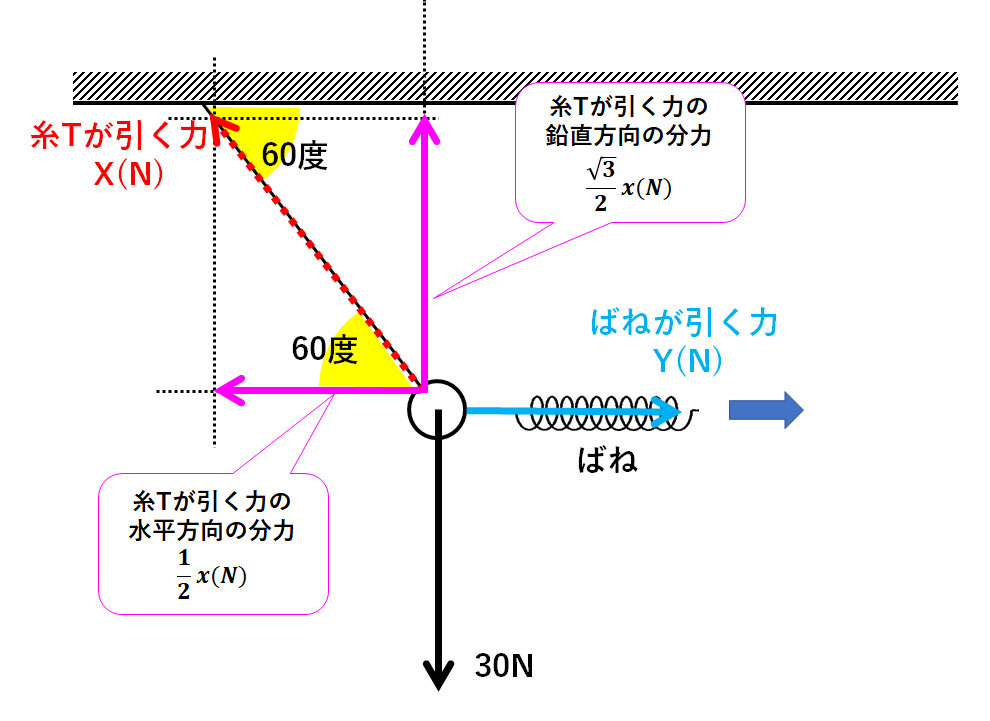
糸Tが引く力を分解しましょう。(↓の図)

またも30度・60度・90度の三角形がかくれています。(↓の図)

糸Tが引く力をx(N)とすると
$$糸Tが引く力の水平方向の分力=x(N)×\frac{1}{2}=\frac{1}{2}x(N)$$

$$糸Tが引く力の鉛直方向の分力=x(N)×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}x(N)$$

ここでばねが引く力をy(N)としましょう。

水平方向の力がそれぞれつり合い、鉛直方向の力もそれぞれつりあっているはずです。

水平方向の力のつり合いから
$$\frac{1}{2}x(N)=y(N)・・・①$$

鉛直方向の力のつり合いから
$$\frac{\sqrt{3}}{2}x(N)=30(N)・・・②$$

②より
$$x=\frac{2}{\sqrt{3}}×30=20\sqrt{3}$$

①より
$$y=\frac{1}{2}×20\sqrt{3}=10\sqrt{3}(N)$$

よって
$$ばねにはたらく力=10\sqrt{3}(N)$$
$$糸Tにはたらく力=20\sqrt{3}(N)$$
となります。

①の方が易しいですが、あまり応用は利きません。
②の方が難しいですが、どの問題にも通用します。

そう難しい入試問題でないならば①の方法で解きましょう。
難しい私立高校を受験するのであれば②の方法で解きましょう。