このページでは2018年度の兵庫県立入試一般選抜の問題を解説しています。(理科のみ)
問題・模範解答はこちら↓↓
https://resemom.jp/feature/public-highschool-exam/hyogo/2018/
大問1の解説
1.(1)
風化と侵食のちがいを理解しておきましょう。
侵食・・・流水のはたらきでけずりとられること。
風化・・・日光や氷結などの自然現象によってぼろぼろになること。
4.(1)
仕事とはエネルギーを変化させることです。
図2では3kgの力学台車を、2m引き上げています。
ここでは位置エネルギーが増加しています。
よってこの場合
$$仕事=位置エネルギーの増加量$$
です。
$$位置エネルギー=重さ(N)×高さ(m) $$
なので
$$位置エネルギーの増加量=30N×2m=60J$$
となります。
4.(2)
一方で仕事とは
$$仕事=力(N)×力の向きに動かした距離(m)$$
でも求められます。
求める力をx(N)とすると
$$仕事=x(N)×5m=5x(J)$$
これが(1)で求めた仕事と等しいので
$$5x(J)=60J$$
x=12となり、12Nが答えになります。
大問2の解説
1.(1)~(3)
マメ科の植物は子葉が発達しており、子葉に栄養をたくわえています。
(無胚乳種子という)
図1のCが子葉にあたります。
この部分にたくわえられた栄養分を使って発芽します。
1.(4)
インゲンマメは双子葉類にあたりますが、
もしそれを知らなくても図2で網目状の葉脈が見られます。(網状脈)
ここから双子葉類と判断すればよいでしょう。
2.(1)
道管・・・・根から吸収した水を運ぶ管。
師管・・・・葉でできた栄養分を運ぶ管。
2.(2)
問いの表の意味を理解しておきましょう。
袋Xでは光があたっていますので
インゲンマメは光合成と呼吸を同時に行っています。
袋Yでは光が当たっていません。
インゲンマメは呼吸しかできません。
袋Xでは袋の中の二酸化炭素が減少しています。
これは光合成を呼吸よりもさかんに行ったためです。
(光合成では外部から二酸化炭素を吸収する・呼吸では外部に放出する)
袋Yでは袋の中の二酸化炭素が増加しています。
これは呼吸のみを行ったからです。
ではそれぞれの選択肢をチェックしてみましょう。
ア
袋Yの数値をチェック。それぞれ袋の中の二酸化炭素の量が
13時から15時 → +0.15
15時から17時 → +0.1
17時から19時 → +0.1
となっているので、呼吸による二酸化炭素の放出は一定ではないことがわかります。
イ
袋Yの数値をチェック。袋の中の二酸化炭素の量が
17時から19時 → +0.1
となっているので、インゲンマメは呼吸をしたことがわかります。
ウ
まず袋Yの数値をチェック。袋の中の二酸化炭素の量が
15時から17時 → +0.1
この時間では、呼吸により0.1の二酸化炭素を放出したとわかります。
次に袋Xの数値をチェック。袋の中の二酸化炭素の量が
15時から17時 → -0.1
この時間では、全体で0.1の二酸化炭素を吸収したとわかります。
まとめると
呼吸によるCO2放出量=0.1
呼吸と光合成全体でのCO2吸収量=0.1
これは
光合成によるCO2吸収量-呼吸によるCO2放出量=0.1(全体でのCO2吸収量)
ということ。
よって
光合成によるCO2吸収量=0.1+0.1=0.2
となります。
したがって光合成で取り入れた二酸化炭素の量と呼吸で出した二酸化炭素の量は等しくありません。
エ
ウの選択肢と同様に考えて、光合成によるCO2吸収量を求めましょう。
13時から15時では・・・
袋Yより
呼吸によるCO2放出量=0.15
袋Xより
呼吸と光合成全体でのCO2吸収量=0.3
よって
光合成によるCO2吸収量=0.15+0.3=0.45
17時から19時では・・・
袋Yより
呼吸によるCO2放出量=0.1
袋Xより
呼吸と光合成全体でのCO2吸収量=0
よって
光合成によるCO2吸収量=0.1+0=0.1
したがって13時から15時での光合成によるCO2吸収量が最も大きいことがわかります。
2.(3)
前問と同様に考えます。
13時から19時では・・・
袋Yが0.80→1.15なので
呼吸によるCO2吸収量=0.35
袋Xが0.80→0.40なので
呼吸と光合成全体でのCO2吸収量=0.40
よって
光合成によるCO2吸収量=0.35+0.40=0.75
となります。
2.(4)
デンプンなどの有機物の量はどれだけ二酸化炭素を吸収したかで決まります。
(吸収した二酸化炭素からデンプンをつくり出す)
袋Xでは、袋の中の二酸化炭素が
13時で0.80 → 15時で0.50 → 17時で0.40 → 19時で0.40
と変化しているので
13時から17時まではデンプンがつくられています。
しかし17時から19時の間はデンプンをつくっていません。
よってイの選択肢が正解となります。
大問3の解説
1.(1)
問題で密度の表が与えられている点に注目。
密度とは質量と体積の関係を表す値。
$$質量=体積×密度$$
$$体積=\frac{質量}{密度}$$
という関係があります。
必ず押さえておきましょう。
この問いでは
「食塩の飽和水溶液の100cm3」と書かれているので
$$水溶液の質量=体積×密度=100cm^3×1.20g/cm^3=120g$$
一方、問題文中に、20℃における食塩の溶解度は35.8とあります。
20℃の水100gに35.8g溶けるということです。
よって求める食塩の量をx(g)とすると
$$(100+35.8)g:35.8g=120g:x(g)$$
(飽和水溶液の質量:溶質の質量という比例式)
x=31.63・・・となります。
よって31.6gが答えです。
1.(2)
$$固体Aの体積=2cm×2cm×2cm=8cm^3$$
なので
$$固体Aの密度=\frac{7.36g}{8cm^3}=0.92g/cm^3$$
よって固体Aは氷であることがわかります。
1.(3)
問題文より
固体Aは液体Bに沈んだ
ことがわかります。
つまり
固体Aの密度>液体Bの密度
であることがわかります。
よって表1より液体Bはエタノールか食用油のどちらかです。
★押さえておこう
物体Xが液体Yに浮く・・・物体Xの密度<液体Yの密度
(XはYよりもスカスカであるということ)
物体Xが液体Yに沈む・・・物体Xの密度>液体Yの密度
(XはYよりもぎゅうぎゅうであるということ)
液体Bは液体Cを加えると混ざり合ったことから
液体Bは食用油であることがわかります。
(エタノールは水に溶けてしまうが、食用油は水に溶けない)
ちなみにエタノールは水にも油にも溶けてしまいます。
1.(4)
図1で使われた液体は混ざり合うことなく2層にわかれているので
ア.水と食用油 または エ.食用油と食塩の飽和水溶液
のどちらかです。
(エタノールは水にも油にも溶けるため)
図1のおもちゃはポリスチレンでできています。
よって表より密度は1.06g/cm3。
おもちゃより下にある液体は、
密度がポリスチレンより大きいので、食塩の飽和水溶液とわかります。
おもちゃより上にある液体は、
密度がポリスチレンより小さいので、水・食用油のどちらかです。
総合するとエの選択肢が正解です。
2.(1)
まずA班の実験では
塩酸20cm3に少しずつ炭酸カルシウムを加える
という実験をしています。
この実験では二酸化炭素が発生します。
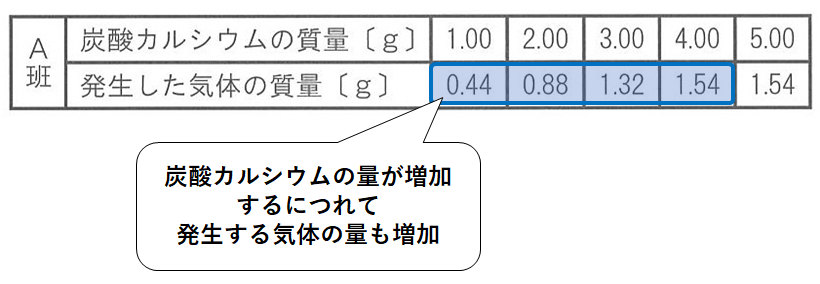
表2のA班の結果に注目。
炭酸カルシウムを増やすほど発生する気体(二酸化炭素)の量が多くなっています。(↓の図)
しかし気体の量はずっと増え続けるわけでなく、1.54gが最大です。(↓の図)
これはうすい塩酸20cm3に反応する炭酸カルシウムには限界があるからです。
(うすい塩酸20cm3に炭酸カルシウムを100kgや200kg入れても、全部は反応しないですよね)
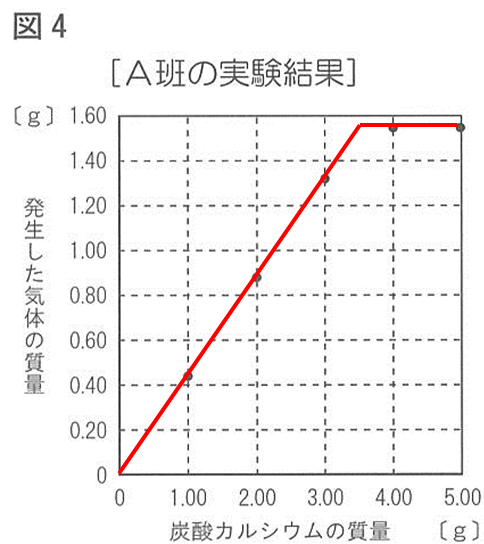
図4のグラフを書いてみましょう。(↓の図)
このグラフから見ても塩酸20cm3と反応する炭酸カルシウムには限りがあることがわかります。
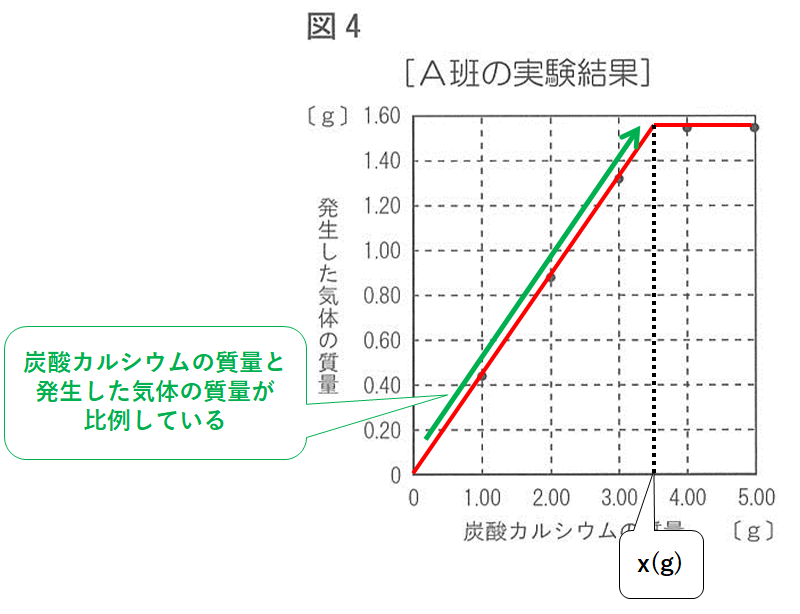
その値をxとしましょう。
このグラフは途中までは比例しているので(↓の図)
$$1.00:0.44=x:1.54$$
よってx=3.5となります。
つまり
塩酸20cm3には炭酸カルシウムが3.5gまで反応し、そのとき1.54gの二酸化炭素が発生する
ことがわかります。
空欄①
炭酸カルシウムを3.00g加えると、すべて反応します。
(塩酸20cm3には炭酸カルシウムが3.5gまで反応するから。)
空欄②
塩酸20cm3には炭酸カルシウムが3.5gまで反応するので、炭酸カルシウムが3.00gでは塩酸が一部反応せずに残っているはず。
つまり溶液全体は酸性。
よってpHは7より小さいことになります。
★pHについて
pHが7・・・中性
pHが7より小・・・酸性
pHが7より大・・・アルカリ性
空欄③
先ほどの計算より3.50gです。
2.(2)
空欄⑤
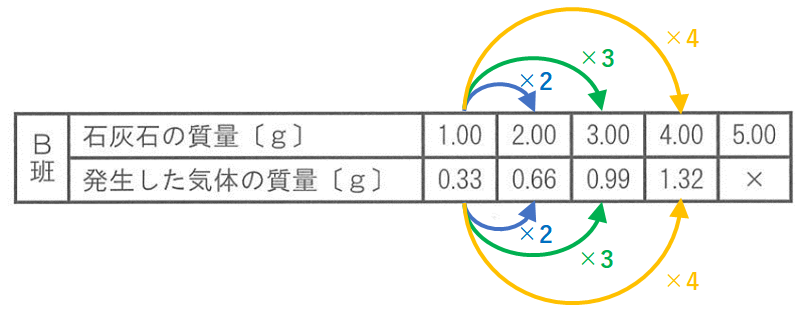
B班の表に注目。
石灰石の質量と発生した気体(二酸化炭素)が比例しているように見えます。(↓の図)
よって石灰石が5.00gのときに発生した二酸化炭素をy(g)とすると
$$1.00g:0.33g=5.00g:y(g)$$
でy=1.65gとなる・・・と思ってはいけません。
A班の実験より
実験で使われている塩酸20cm3からは二酸化炭素が最大で1.54gまでしか発生しないのです。
よって石灰石5.00gのときに発生した二酸化炭素も1.54gとなります。
2.(3)
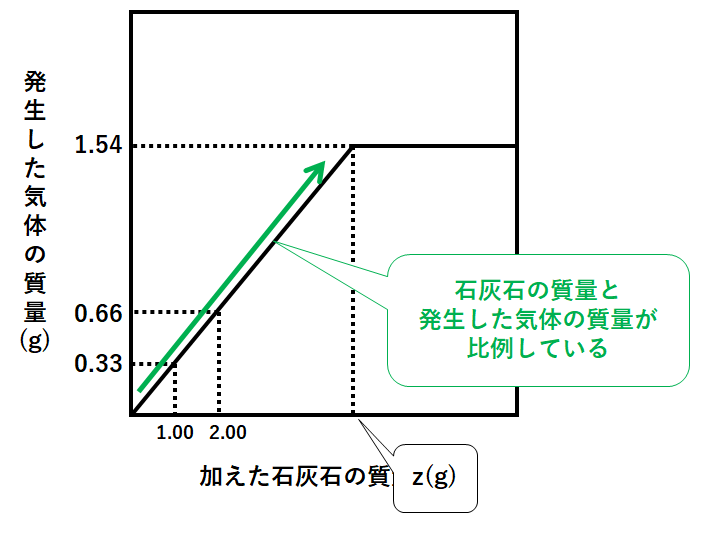
図4と同様に石灰石の質量と発生した二酸化炭素の関係をグラフにすると↓の図のようになります。
ここで塩酸20cm3と反応する石灰石をz(g)とすると
このグラフは途中まで比例しているので(↓の図)
$$1.00g:0.33g=z(g):1.54$$
よってz=4.666・・・≒4.67gとなります。
空欄⑥
空欄⑤より
塩酸20cm3には石灰石4.67gまで反応し、二酸化炭素が1.54g発生する
ことがわかります。
また(1)(2)より
塩酸20cm3には炭酸カルシウムが3.5gまで反応し、二酸化炭素が1.54g発生する
こともわかっています。
石灰石の主成分は炭酸カルシウムですが、不純物が混じっています。
(はじめの問題文に書いてあります。)
二酸化炭素1.54g発生させるのに
炭酸カルシウム → 3.5g必要。
石灰石 → 4.67g必要。
ということは石灰石4.67gには炭酸カルシウムが3.5g含まれているはず。
石灰石4.67gと塩酸20cm3を反応させる。
↓↓↓
石灰石の中の炭酸カルシウムが全部反応して二酸化炭素1.54g発生した
という理屈です。
よって石灰石に含まれる炭酸カルシウムの割合は
$$\frac{3.5}{4.67}×100=74.94・・・$$
となり、ほぼ75%になります。
空欄⑦
C班の実験では9.00gの炭酸カルシウムを用意しています。
これと過不足なく反応する塩酸をw(cm3)とすると
塩酸20cm3には炭酸カルシウムが3.5gまで反応することがわかっていますから
$$20cm^3:3.5g=w(cm^3):9$$
となりw=51.42・・・≒51.4cm3です。
大問4の解説
1.(1)
単位がWh(ワット時)の場合の電力量は
$$電力量(Wh)=電力(W)×時間(h)$$
で求められます。
★単位がJ(ジュール)の場合の電力量・熱量は
$$電力量・熱量(J)=電力(W)×時間(s)$$
で求められます。
よって
$$2分=\frac{2}{60}時間$$
なので
$$1200W×\frac{2}{60}時間=40Wh=0.04kWh$$
となります。
1.(2)
与えられている公式を使います。
$$水の質量=1200g$$
$$水の上昇温度=24℃$$
$$電気ポットの電気エネルギー=1200W×120秒=144000J$$
なので
$$\frac{4.2×1200g×24℃}{144000J}×100=84%$$
となります。
1.(3)
すべての変換効率を求めれば済む話ですが、やや計算が面倒です。
よって公式の
$$\frac{水の質量(g)×水の上昇温度(℃)}{電力(W)}$$
の部分だけ計算する方が楽です。
2.(1)
オームの法則より
$$\frac{6V}{0.409A}=14.66・・・≒14.7Ω$$
2.(2)
水の上昇温度は発生する熱量によって決まります。
また熱量は
$$熱量(J)=電力(W)×時間(s)$$
で求められます。
よって電力がどう変化するかを見てみましょう。
電圧を2倍にすると、抵抗に流れる電流が2倍になります。(オームの法則)
$$電力(W)=電流(A)×電圧(V)$$
なので
電圧が2倍になったとき、電力は4倍になるはずです。
電力が4倍になれば発生する熱量も4倍、水の温度上昇も4倍です。
図2では4分間で水温が1℃上昇していますので、
電圧を2倍にすると、4分間で4℃上昇します。
つまりエのグラフが正解です。
2.(3)
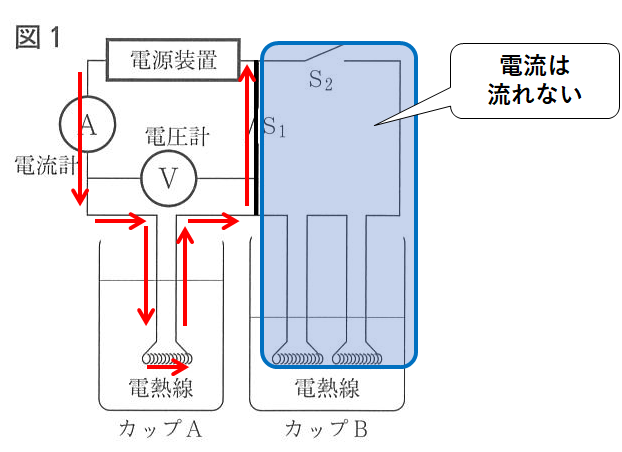
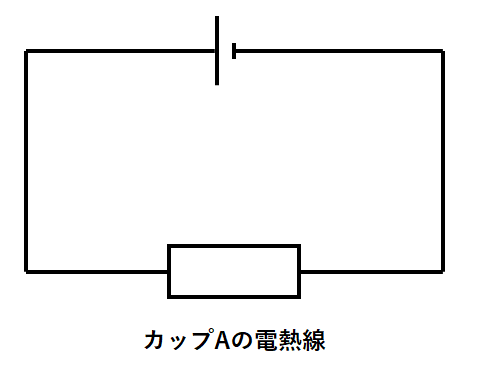
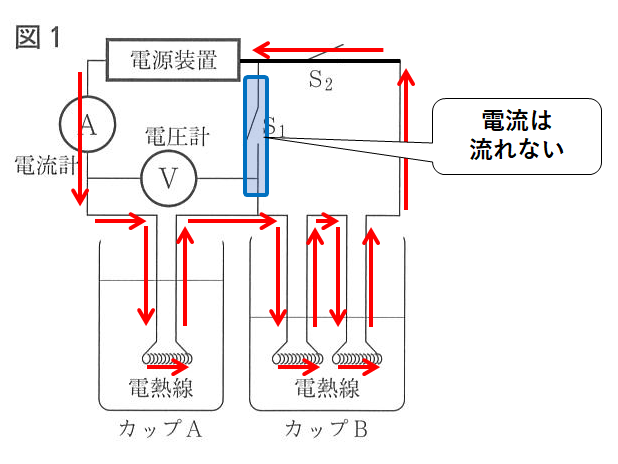
スイッチS1だけをONにしたとき、カップAの電熱線にしか電流は流れません。(↓の図)
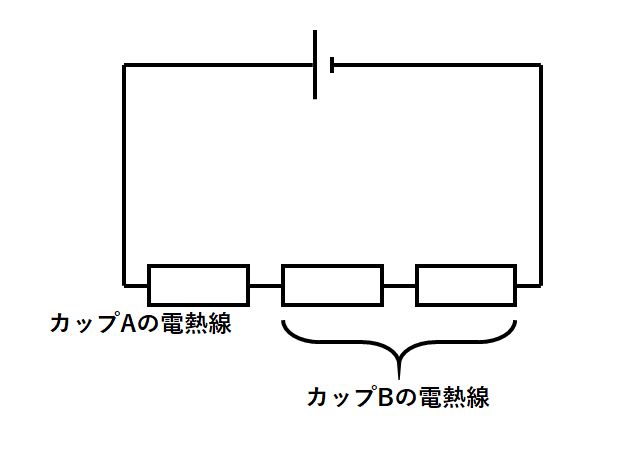
この場合の回路を単純化すると↓のようになります。
スイッチS2だけをONにしたとき、カップAの電熱線にもカップBの電熱線にも電流が流れます。(↓の図)
この場合の回路を単純化すると↓のようになります。
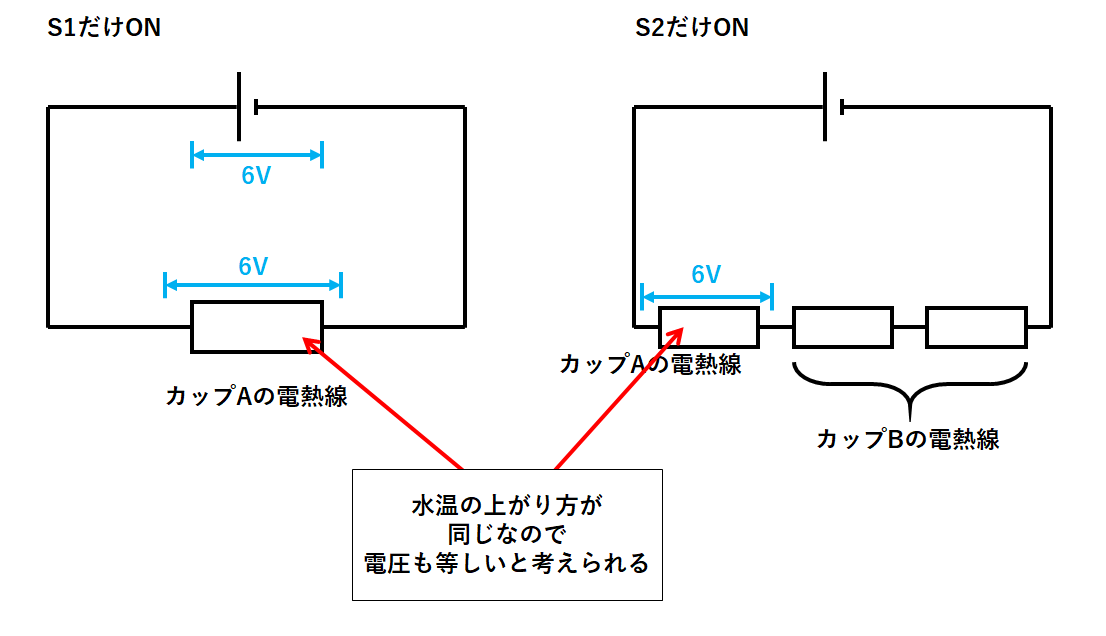
スイッチS1だけONのとき、スイッチS2だけONのときの両方で、カップAの水温の上がり方が同じであることに注目。
スイッチS1だけONのときは電源の電圧が6Vでした。
このときカップAの電熱線には6Vの電圧がかかります。
スイッチS2だけONのときも同じように水温が上がるので、カップAの電熱線には6Vの電圧がかかっていることになります。(↓の図)
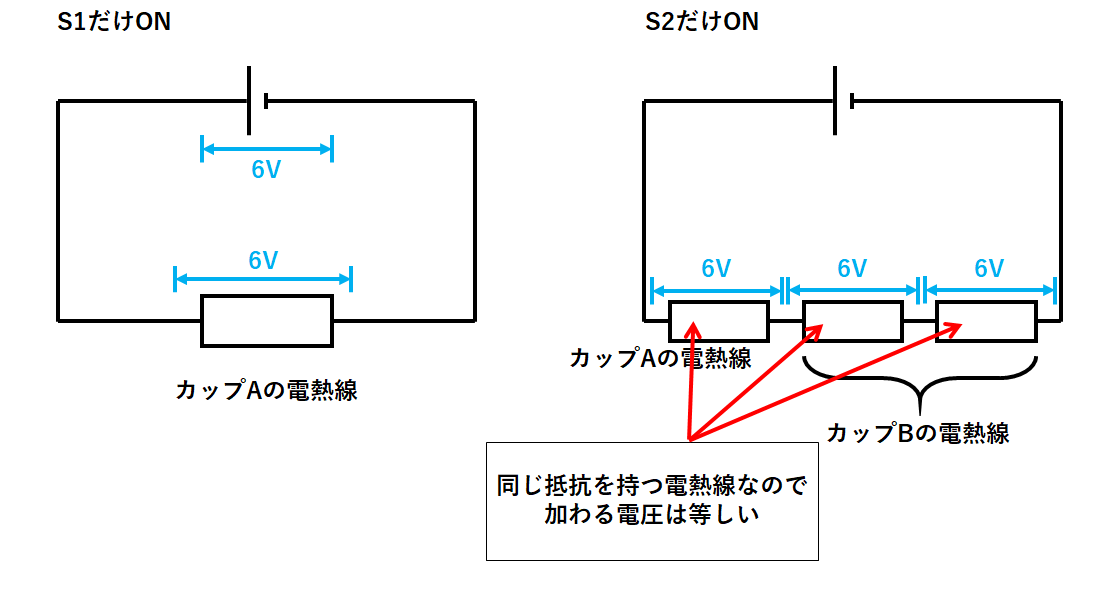
ここで、回路中の3つの電熱線はすべて同じものであることを考えると
カップBの電熱線1つあたりにも6Vの電圧が加わっていることになります。(↓の図)
よって電源の電圧が18Vであることがわかります。
2.(4)
直列につながれているのでカップAとカップB全体で流れる電流は同じです。
また(3)より、カップAには6V、カップBには12Vの電圧がかかるので(↓の図)
カップAの電力とカップB全体の電力の比は1:2になっています。
ということはカップBでの発熱量はカップAの2倍。
よってカップBの水温上昇はカップAの2倍になるはず。
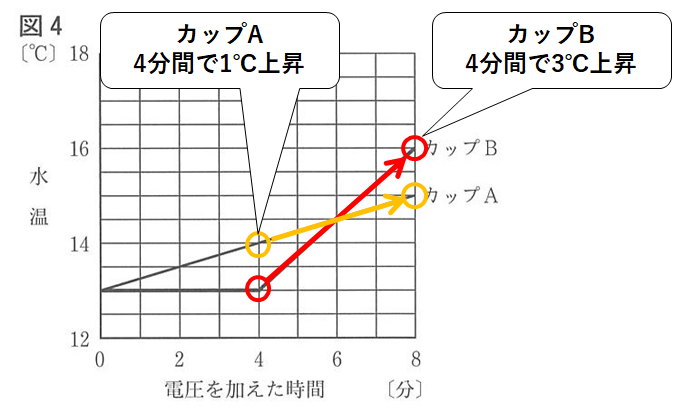
ですが、図4のグラフを見るとそうなっていません。(↓の図)
4分後~8分後で
カップA・・・1℃上昇
カップB・・・3℃上昇
ですので
カップBの水温上昇はカップAの3倍です。
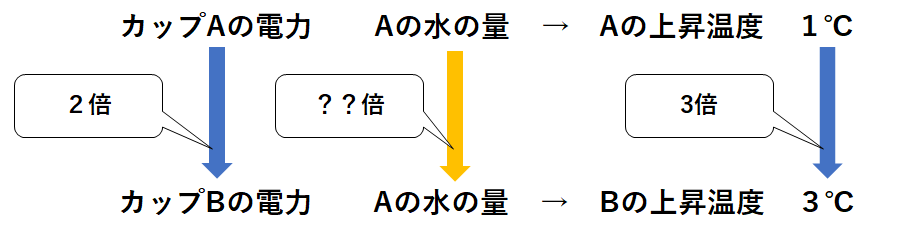
ここで水の温度の上がり方について。
水の上昇温度は、熱量に比例し、水の量に反比例します。
よっていま
水の上昇温度は3倍・熱量は2倍
なので水の量は3分の2倍であることがわかります。
よって
$$\frac{2}{3}=0.666・・・≒0.67倍$$
となります。
大問5の解説
1.(1)
図2のテープでわかっているのは
×印が8時30分から16時30分までの2時間ごとの太陽の位置を記録したもの
ということだけです。
1.(2)
東経135度の地点の方が西にあるので、
東経135度の地点では観測地点より太陽の南中が遅いです。
観測地(東経135.25度)と東経135度の経度の差は
$$135.25-135=0.25度$$
太陽の日周運動は1時間で15度ずつ動くので、南中時刻の差をx(分)とすると
$$60分:15度=x分:0.25度$$
よってx=1分となります。
したがって東経135度の地点での南中時刻は12時14分となります。
★経度差が1度あると南中時刻は4分ずれます。
東経が1度大きい→南中時刻が4分はやい
東経が1度小さい→南中時刻が4分おそい
覚えておくと便利です。
1.(3)
図1の透明半球上の記録は、冬の記録であると考えられます。
(日の出・日の入りの位置が真東・真西より南寄りであるため。)
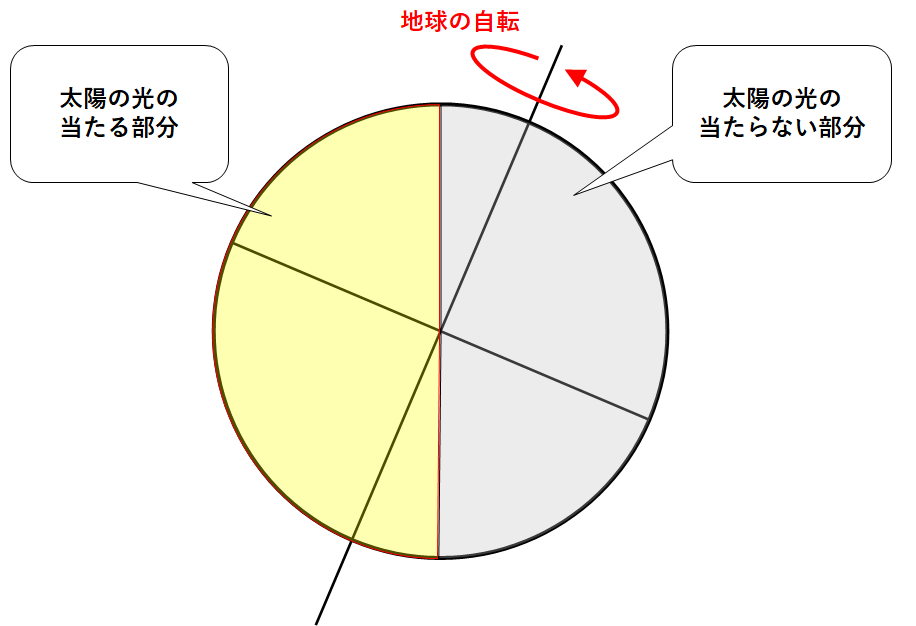
冬の時期、地球に太陽からの光は↓の図のように当たっています。
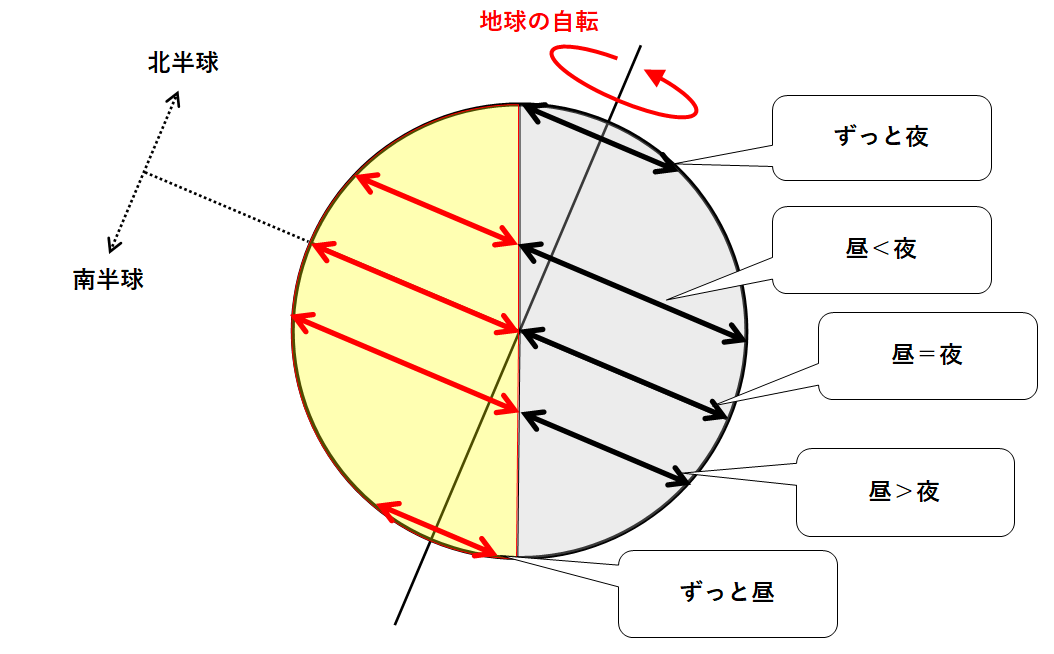
この図に地球の自転を考えると・・・
日本では
昼の長さ<夜の長さ
となっています。
北極付近ではずっと夜。
(太陽が昇らない。極夜といいます。)
南半球では
昼の長さ<夜の長さ
となっています。
南極付近ではずっと昼。
(太陽が沈まない。白夜といいます)
このようになっているのはウ・エのみです。
また図1のBの位置は明け方を終えた(日の出が終わった)時間帯です。
よって日本が日の出が終わったあととなっているのはウです。
1.(4)
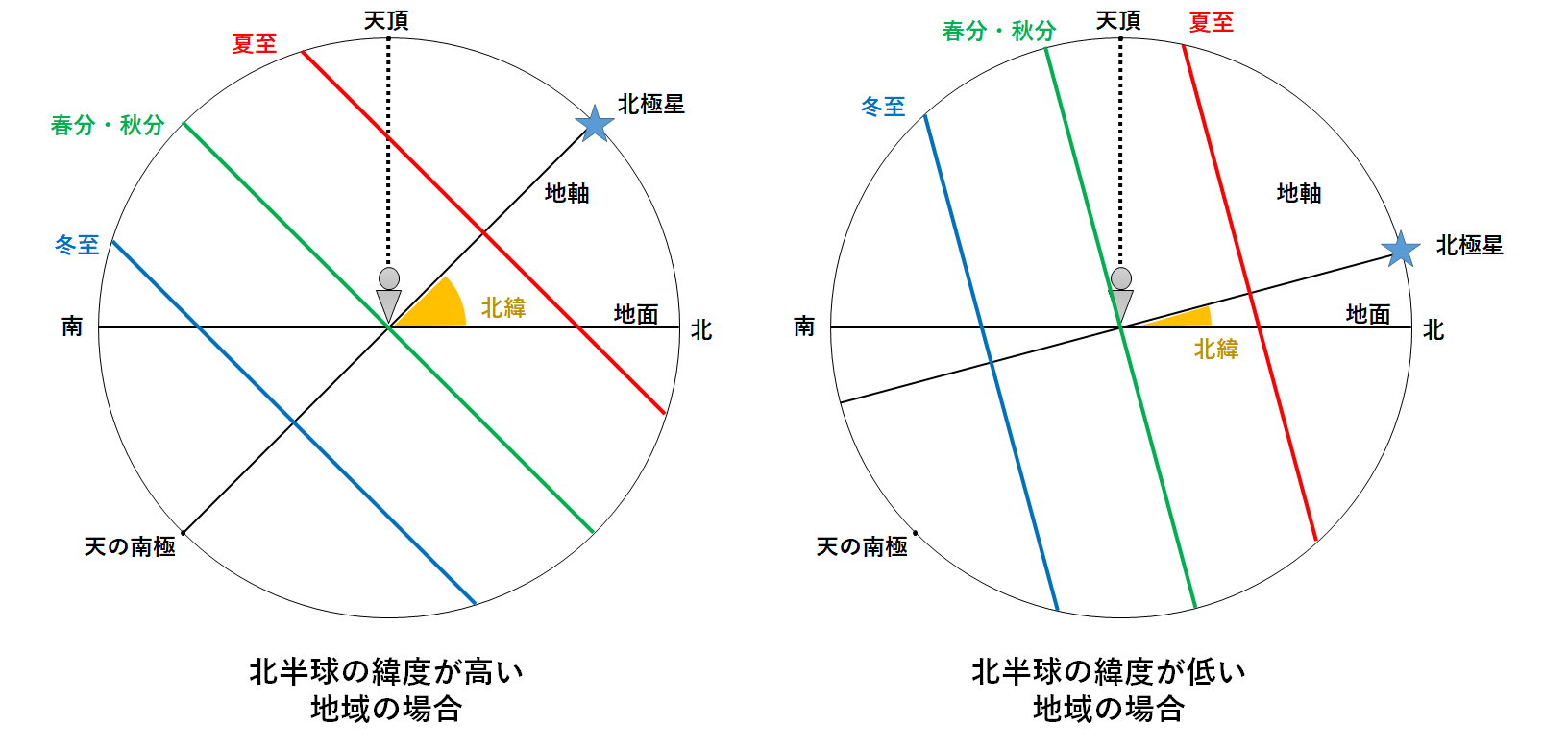
神戸と沖縄では緯度(北緯)が異なります。
神戸の方が沖縄よりも緯度(北緯)が大きいです。
そのため太陽の日周運動の記録が異なります。(↓の図)
★緯度による南中高度のちがい
北にある(=北緯が大きい)地点ほど、太陽の南中高度は低い。
南にある(=北緯が小さい)地点ほど、太陽の南中高度は高い。
これは南中高度の公式
春分秋分:90-北緯 夏至:90-北緯+23.4 冬至:90-北緯-23.4
をもとにすれば判断できることでもあります。
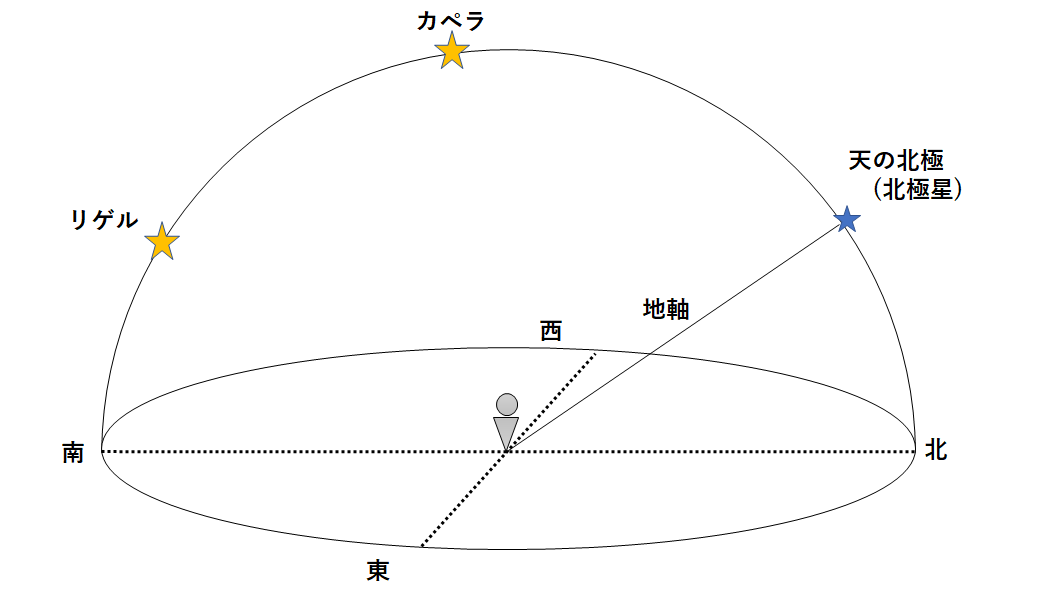
2.(1)
カペラが天頂付近、リゲルが南の空に見えているので、
これを透明半球に表してみましょう。(↓の図)
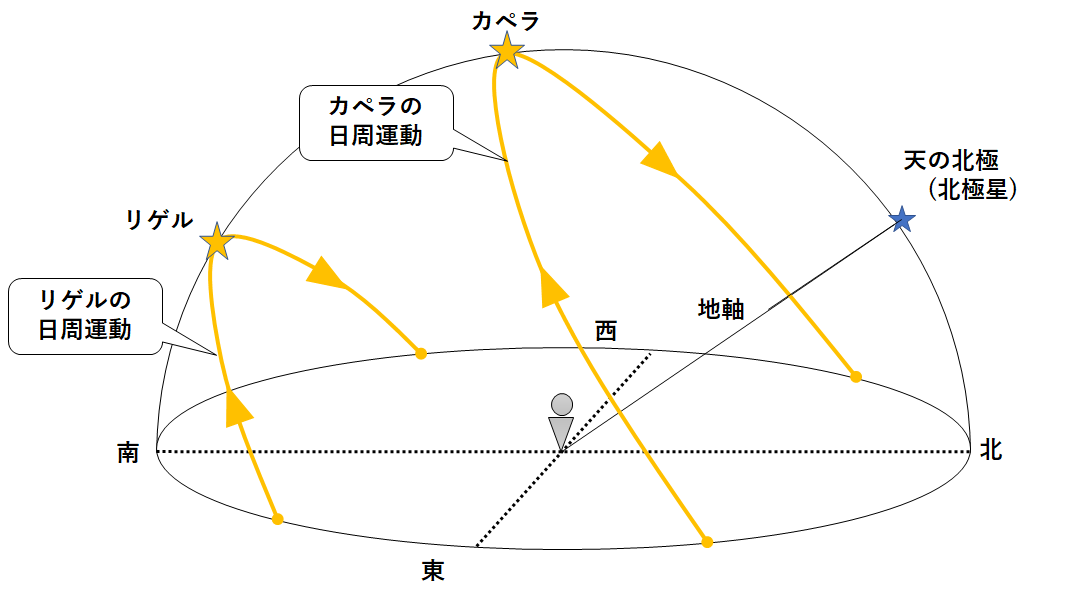
すべての天体は地軸を中心に回転しているように見えます(日周運動)。
その動きを書き足すと↓のようになります。
よってカペラの方がリゲルよりも見えている時間が長いです。
つまりカペラが先に出て、後に沈むことになります。
2.(2)
この問いでは日周運動と年周運動について押さえておく必要があります。
次を押さえたうえで問題を解きましょう。
★日周運動と年周運動
日周運動・・・星が1時間で15度ずつ動くように見える。(地球の自転が原因)
年周運動・・・星が1ヶ月で30度ずつ動くように見える。(地球の公転が原因)
問題文の条件をまとめると
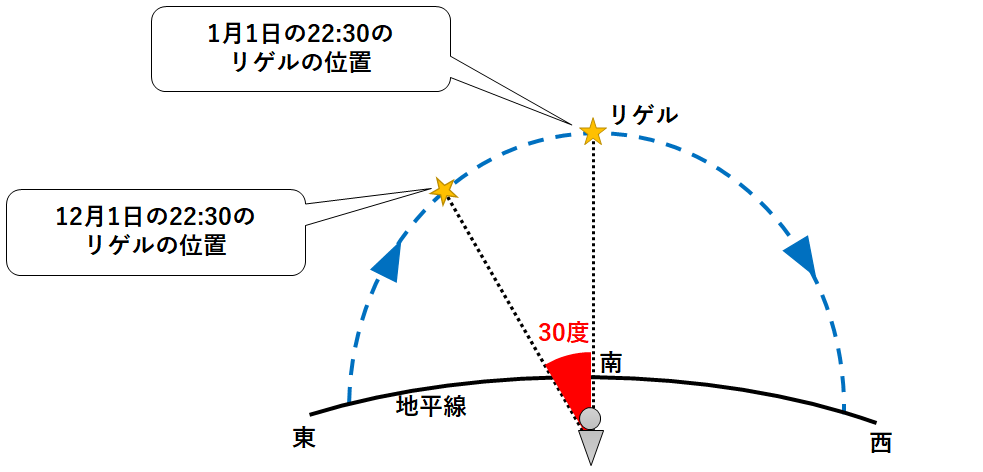
1月1日の22:30にリゲルが南の空に見えた
ということ。(↓の図)
12月1日の何時に点の子午線上に見えるか考えます。
12月1日の22:30では、年周運動によりリゲルが東に30度ずれた位置に見えます。(↓の図)
日周運動を考えると、これが天の子午線に来る(=つまり南中)のは12月1日の24:30となります。
ア・イの選択肢はどちらも正しくないのがわかります。
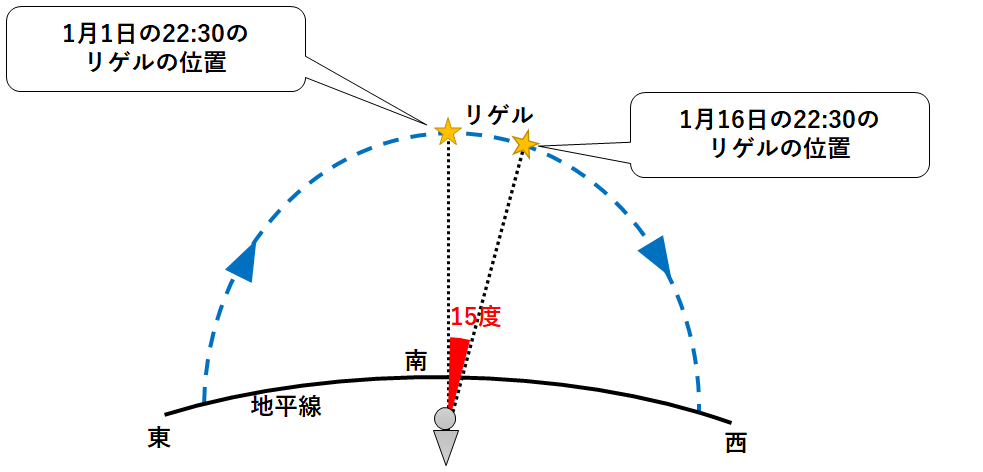
次に1月16日の何時に点の子午線上に見えるか考えます。
1月16日の21:30では、年周運動によりリゲルは西に15度ずれた位置に見えます。(↓の図)
日周運動を考えると、これが南中していたのは21:30となります。
3.(1)
図4の中のいて座に注目しましょう。
(どの星座で考えても構いません。)
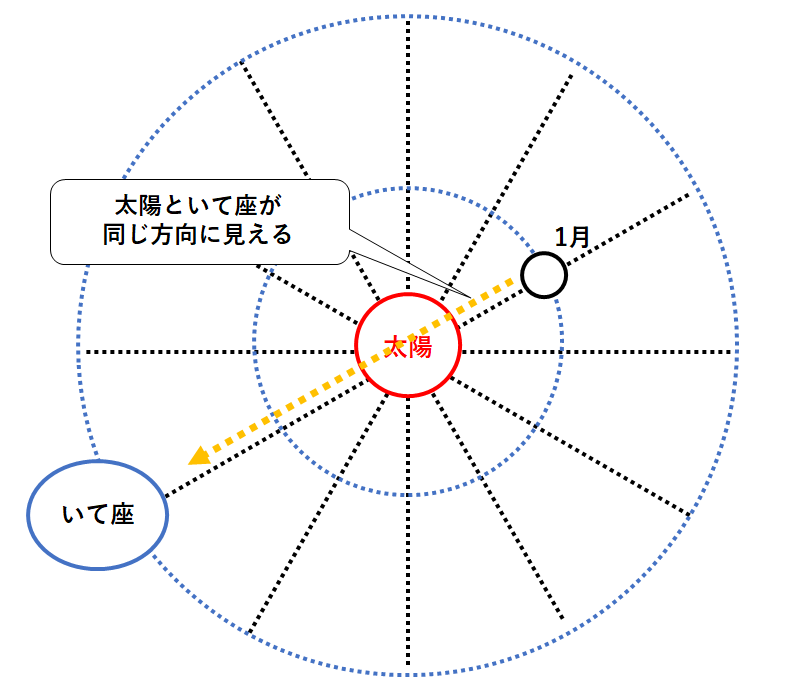
1月の太陽と地球・いて座の位置関係は↓のようになっています。(北極の上空から見た位置関係)
図4は、1月に太陽を見ると、いて座と同じ方向に見えるということを意味しているんですね。
2月にはやぎ座の方向に太陽が見えています。
2月の太陽と・地球・やぎ座の位置関係は↓のようになっているのです。
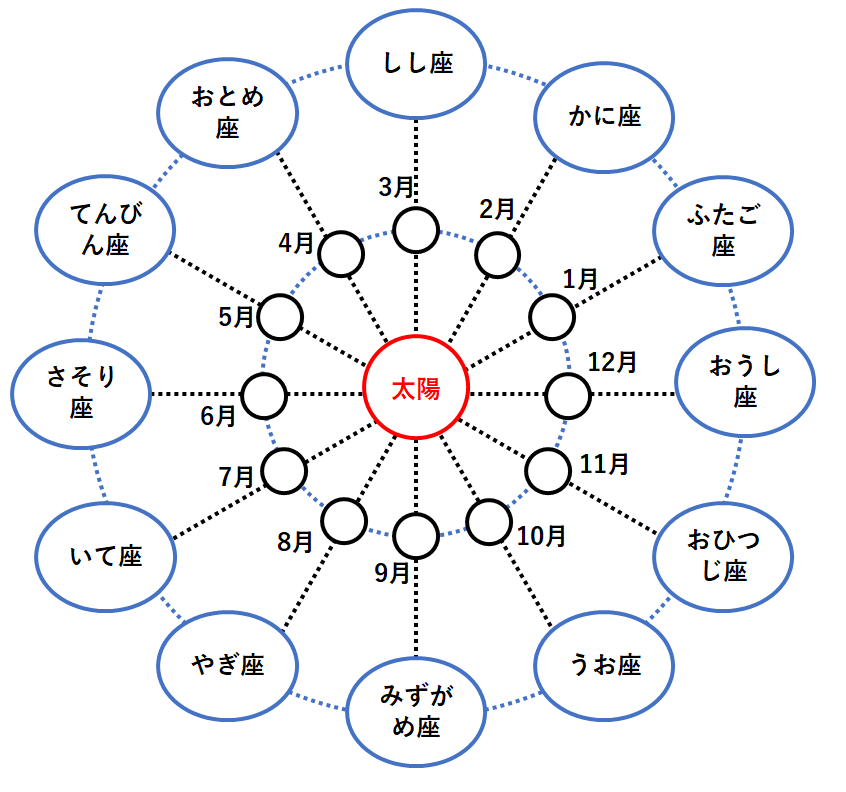
ほかの星座の位置関係も表してみると↓のようになっています。(北極の上空から見た位置関係)
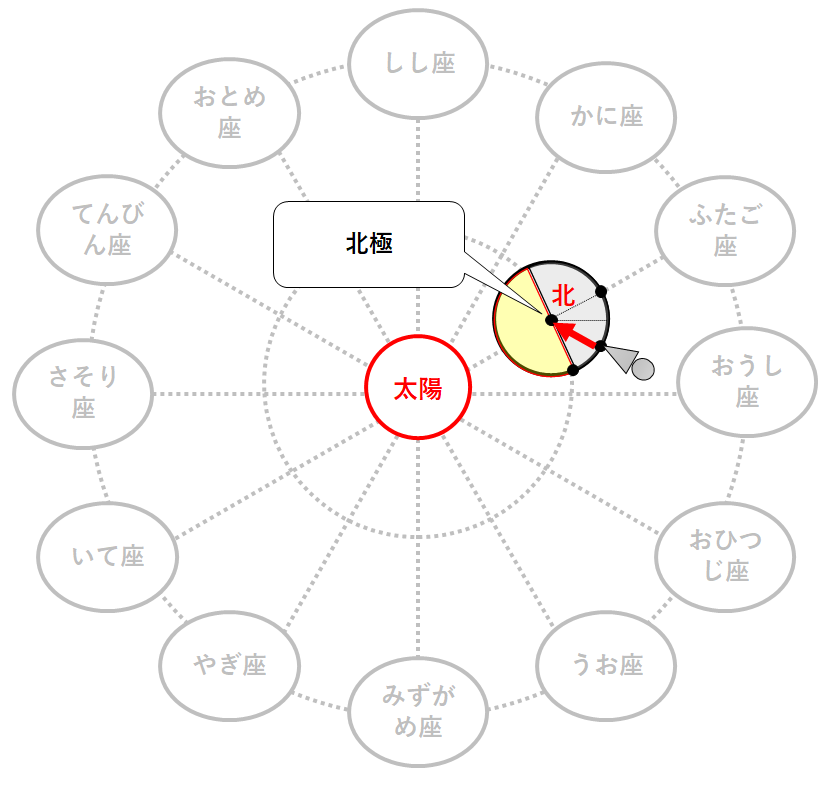
ここで1月1日の地球の位置に注目。(↓の図)
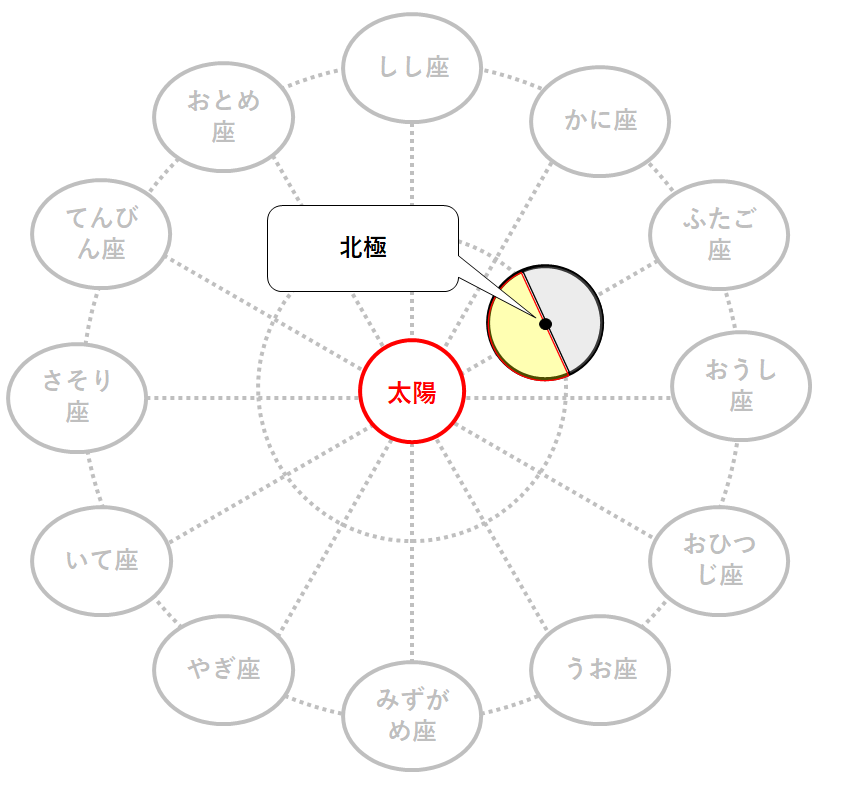
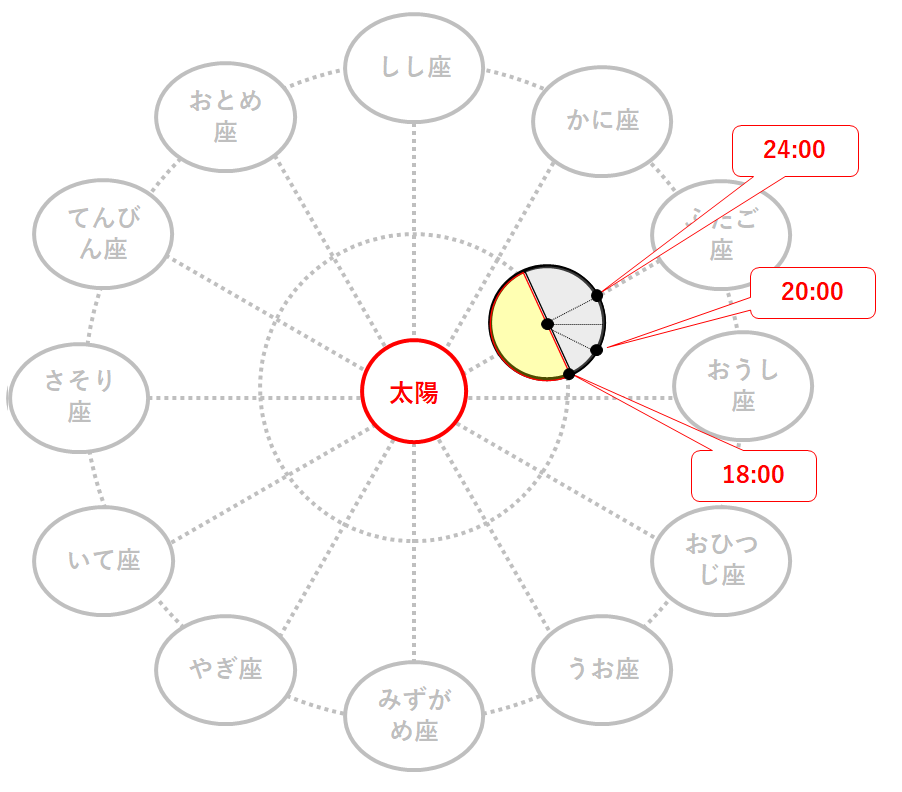
20:00を迎えているのは以下の地点。
この観測者から見た北は北極の方角。(↓の図)
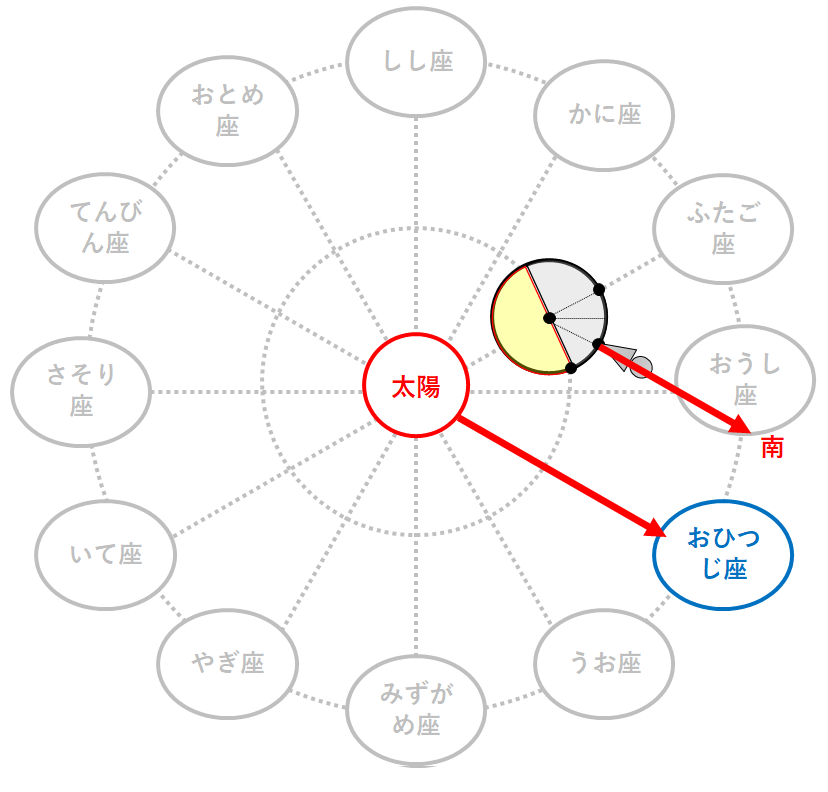
南の方向に見える星座は・・・
↓の図より
おひつじ座とわかります。
3.(2)
1月31日は2月1日にひじょうに近いので、2月1日として考えます。
2月1日の地球と、月食となった月(=新月)の位置関係は↓のようになっています。
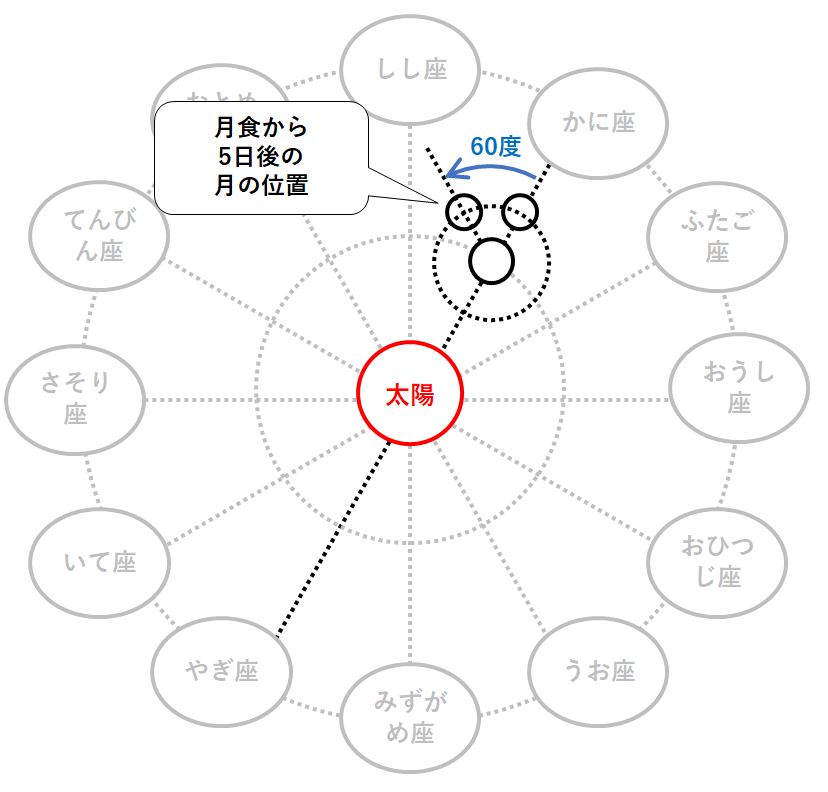
ここから5日後。
月は約60度公転しています。
★月の公転周期
月は約1ヶ月で地球のまわりを公転する。
そのため30日で360度公転していると考えると、1日あたりの動きは12度。
月が60度公転したときの位置関係は↓。
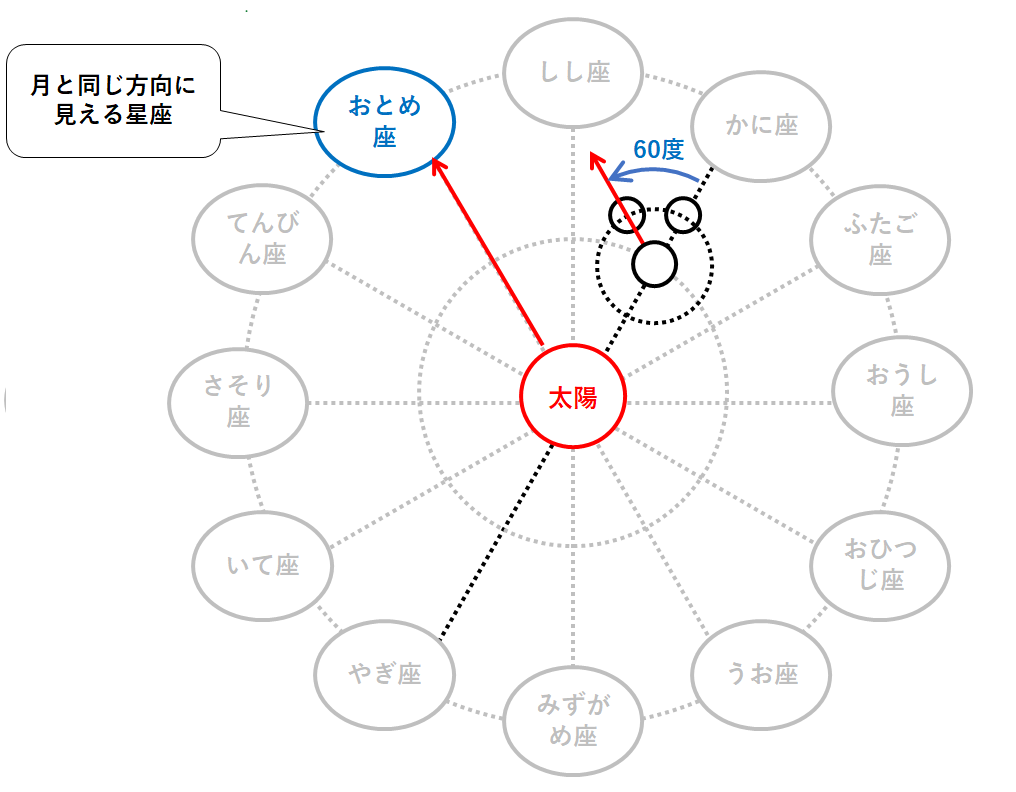
月と同じ方向に見える星座は・・・
図のように、おとめ座となります。









コメント(承認された場合のみ表示されます)