中3地学【*惑星の会合周期】

このページでは火星の会合周期を中心に、惑星の会合周期の問題を中学生にもわかるように解説しています。

 

少し発展的な内容を含みます。

 

惑星に関する基本的なことがらは→【太陽系の天体】←を参考にしてください。

 

金星の見え方・満ち欠けに関しては→【金星の見え方】←を参考にしてください。

 

 

1．会合周期とは

■会合周期

2つの惑星がある位置関係になってから、再びその位置関係になるまでの周期（期間）のこと。

 

 

 

金星のような内惑星は、地球よりも内側を公転しています。

その様子は↓のようになっています。

 

 

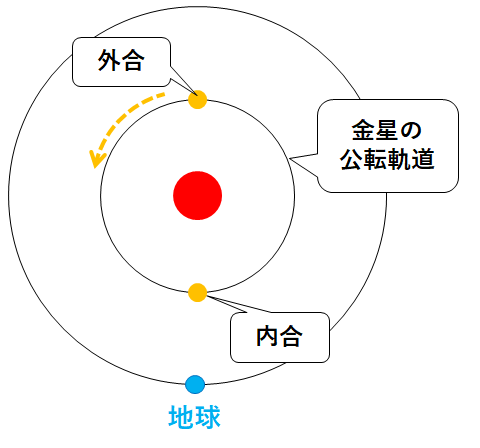
金星が最も地球に近い位置に来たときを内合といいます。

また最も地球から遠い位置に来た時を外合といいます。

（覚える必要はありません）

 

 

 

一度内合という位置関係になってから、再び内合の位置関係になるまでの期間、

あるいは

一度外合という位置関係になってから、再び外合の位置関係になるまでの期間

が会合周期です。

 

 

 

火星のような外惑星の場合は、地球よりも外側を公転しています。

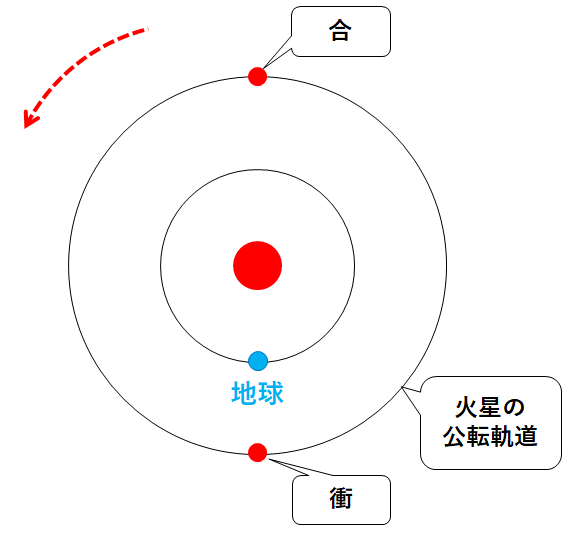
火星が最も地球に近い位置に来たときを衝、最も地球から遠い位置に来た時を合といいます。(↓の図)

 

一度合という位置関係になってから、再び合という位置関係になるまでの期間、

あるいは

一度衝という位置関係になってから、再び衝という位置関係になるまでの期間

が火星のような惑星の会合周期です。

 

 

 

このページでは火星の会合周期を考えてみます。

 

 

火星の公転周期を考える

まずは火星の公転周期について。

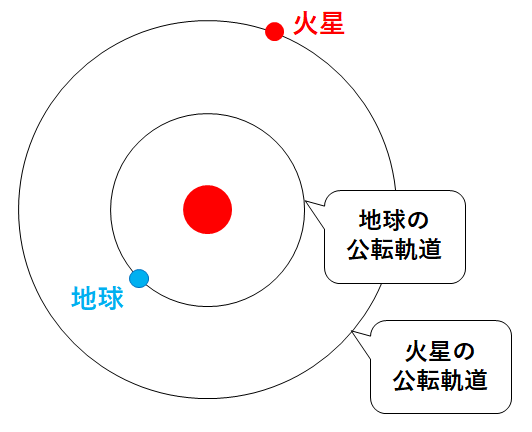
先述の通り、火星は地球よりも外側を公転している外惑星です。(↓の図)

 

 

火星の公転周期（火星が360度公転するのにかかる時間）は約1.8年です。

（正確には1.88年ですがここでは簡単にするために1.8年とします。）

 

 

 

1年＝12ヶ月なので1.8年は

$$1.8年×12ヶ月=21.6ヶ月$$

です。

 

 

 

火星は21.6ヶ月で360度公転します。

 

 

 

ここで火星の1ヶ月あたりに公転する角度を求めます。

 

 

 

それをx度とすると

$$21.6ヶ月:360度=1ヶ月:x度$$

 

 

 

これを解いて

$$x=16.666・・・$$

 

 

 

よって火星は1ヶ月あたり約17度公転します。

 

 

 

地球の公転周期を考える

次に地球の公転周期について。

 

 

 

地球の公転周期（地球が360度公転するのにかかる時間）は1年です。

 

 

 

1年＝12ヶ月なので、地球が1ヶ月あたりに公転する角度をy度とすると

$$12ヶ月:360度=1ヶ月:y度$$

 

 

 

これを解いて

$$y=30度$$

 

 

 

したがって地球は1ヶ月あたり30度公転します。

 

 

 

会合周期を求めよう

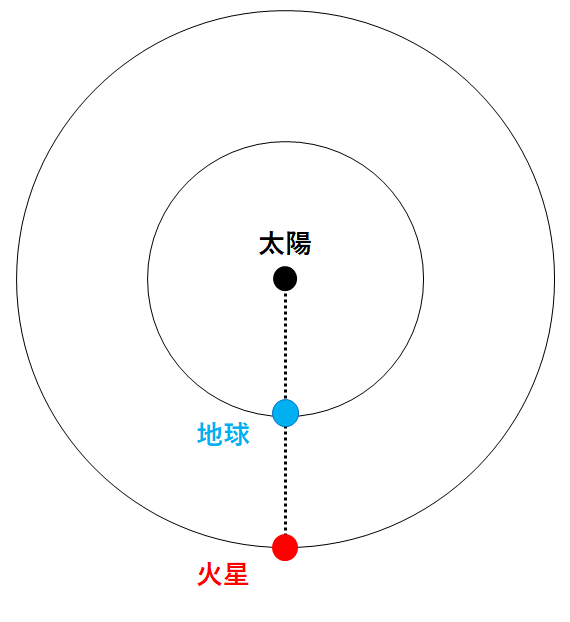
地球・火星・太陽が↓のような位置関係にあるとき（衝という位置関係です）、再びこの位置関係にもどるのにかかる時間を求めましょう。

 

 

まず1ヶ月後。

 

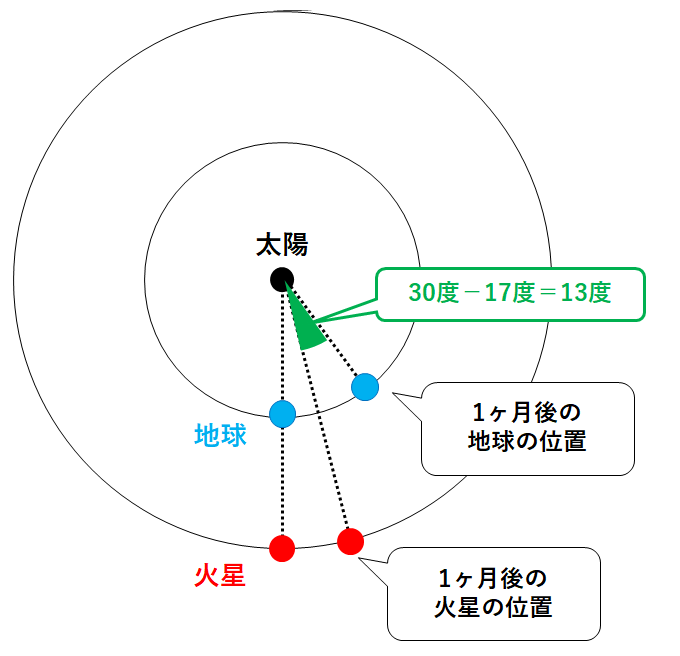
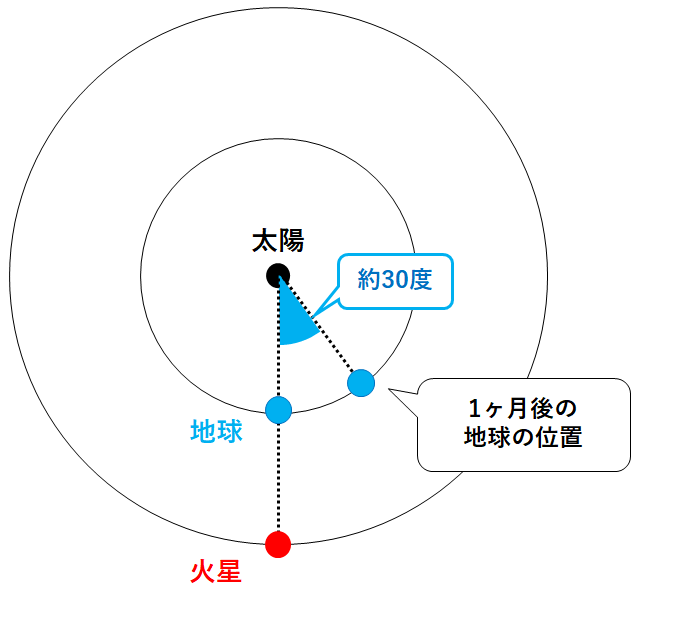
前項で計算した通り、地球は30度公転しています。（↓の図）

 

 

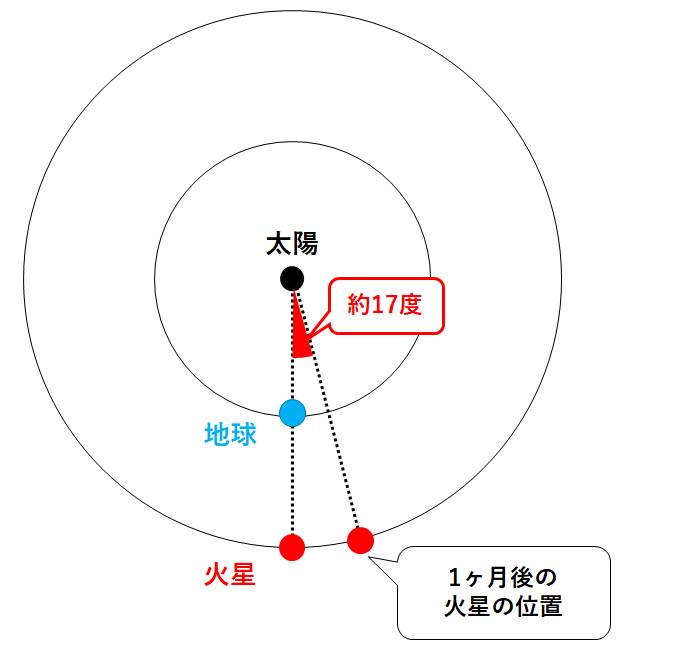
また火星は約17度公転しています。（↓の図）

 

 

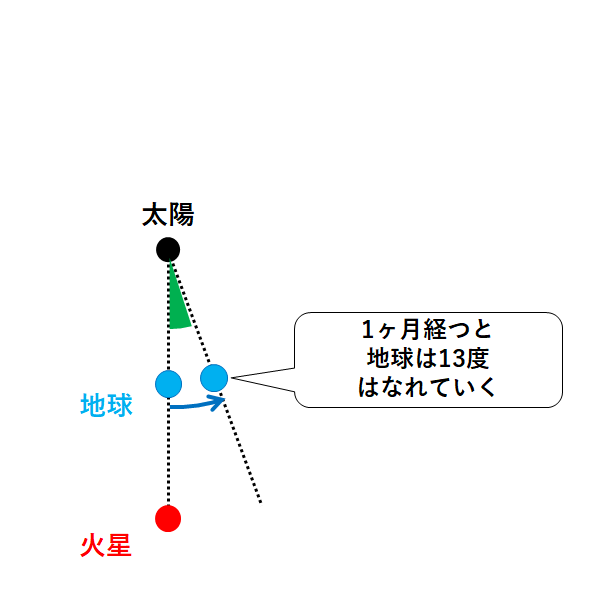
よって1ヶ月後では、地球は火星よりも 30度－17度＝13度 だけ多く公転します。(↓の図)

 

 

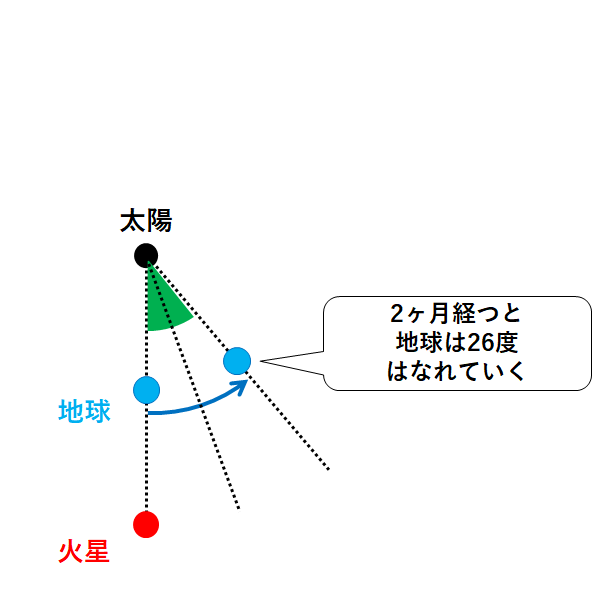
2ヶ月後は、地球は火星よりも13×2＝26度多く公転します。

 

3ヶ月後は、地球は火星よりも13×3＝39度多く公転します。

 

 

 

火星の動きを止めると、地球は

1ヶ月では13度離れていき、

 

 

2か月では26度離れていき、

 

3ヶ月では39度離れていき・・・

 

 

 

このまま360度離れていくと・・・地球と火星は衝の位置関係にもどります。

 

 

 

360度離れていくまでにzヶ月かかるとすると

$$1ヶ月:13度=zヶ月:360度$$

$$z=27.69・・・$$

 

 

 

よって約28か月（＝約2年2か月）かかることになります。

 

 

 

この約28か月（＝約2年2か月）が火星の会合周期となります。