このページでは太陽の南中高度の公式の紹介とその求め方を説明します。
動画による解説はこちらから↓↓↓
チャンネル登録はこちらから↓↓↓
1.太陽の南中高度の公式
■南中高度
太陽が真南の空(天の子午線上)に来たときの太陽の地平線からの角度のこと。
※90度より小さい方を答えるのが一般的です。
■太陽の南中高度の公式(北半球の場合)
▼春分(3月20日ごろ)・秋分(9月20日ごろ)
南中高度=90°-x°
▼夏至(6月20日ごろ)
南中高度=90°-x°+23.4°
▼冬至(12月20日ごろ)
南中高度=90°-x°-23.4°
※ xは観測地点の北緯とする。
※ 地軸が公転面の垂直方向に対して23.4度傾いているとする。
※計算結果が90度を超える場合は、求まった値を180度から引きましょう。
■*南半球での太陽が最も高くなった時の高度の公式
南緯23.4度以上の土地で太陽を観測した場合、太陽は北の空を通ります。
この場合の高度も、太陽の地平線からの角度のうち、90度より小さい方を意味します。
(無理やりいうならば北中高度)
春分(3月20日ごろ)・秋分(9月20日ごろ)
最も高くなった時の高度=90-x
夏至(6月20日ごろ)
最も高くなった時の高度=90-x-23.4
冬至(12月20日ごろ)
最も高くなった時の高度=90-x+23.4
※ xは観測地点の南緯とする。
※ 地軸が公転面の垂直方向に対して23.4度傾いているとする。
※計算結果が90度を超える場合は、求まった値を180度から引きましょう。
2.南中高度の公式の証明・求め方(北半球)
春分・秋分の場合
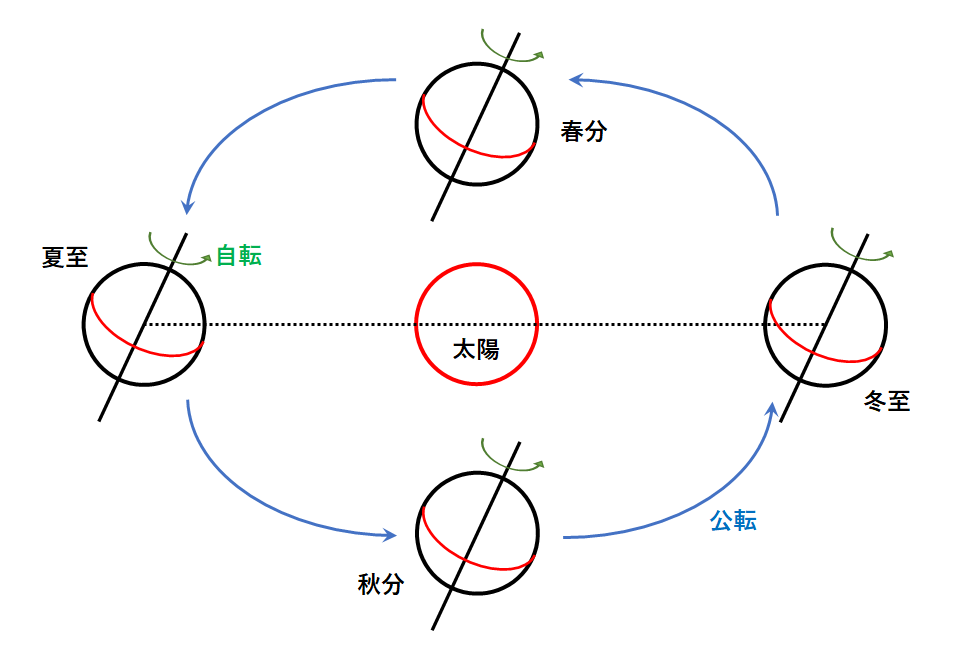
各季節の地球の位置は以下のようになります。
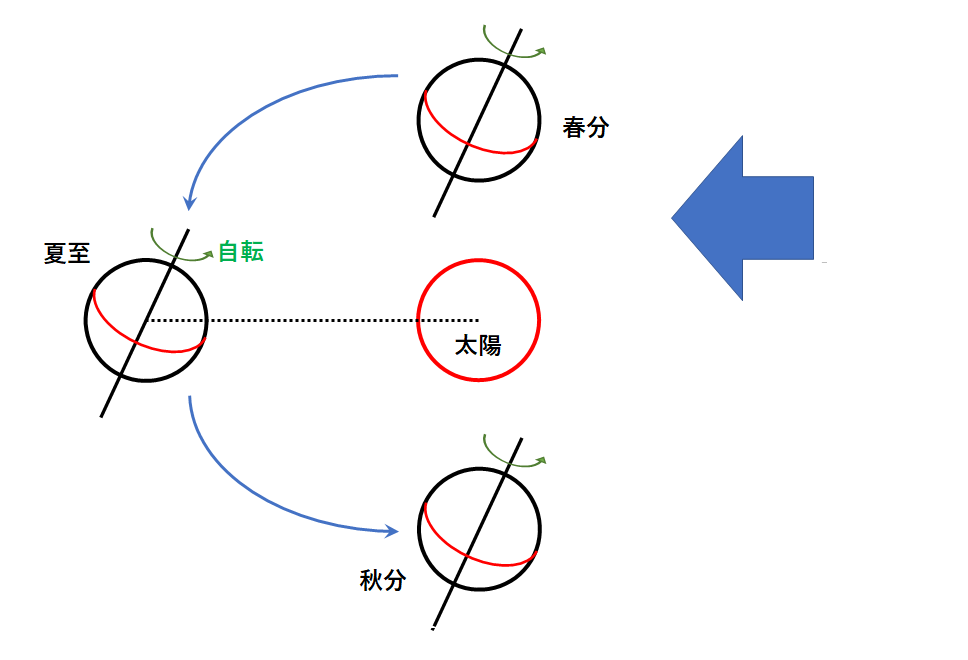
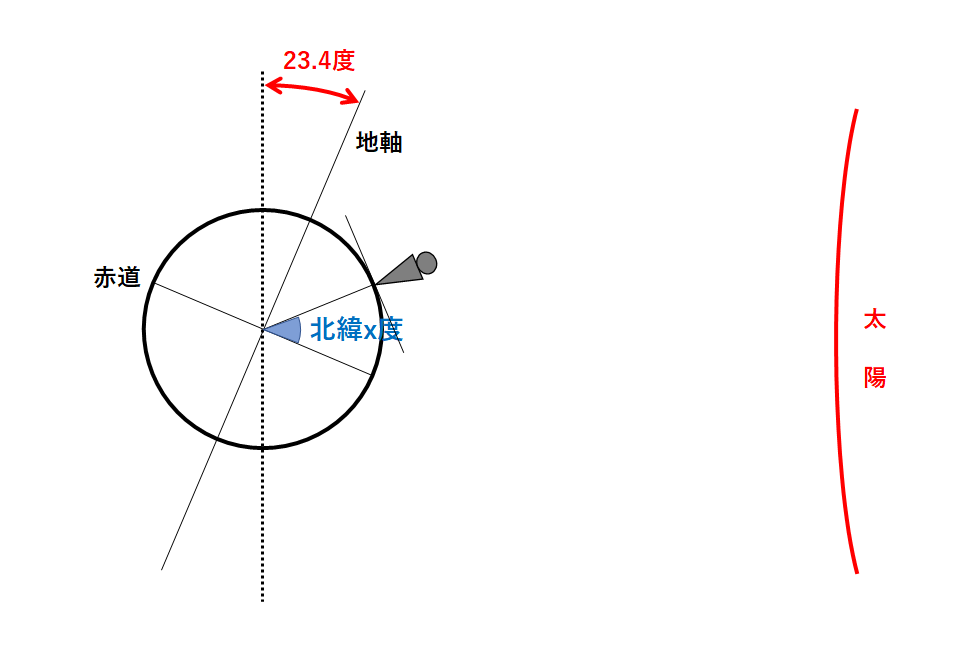
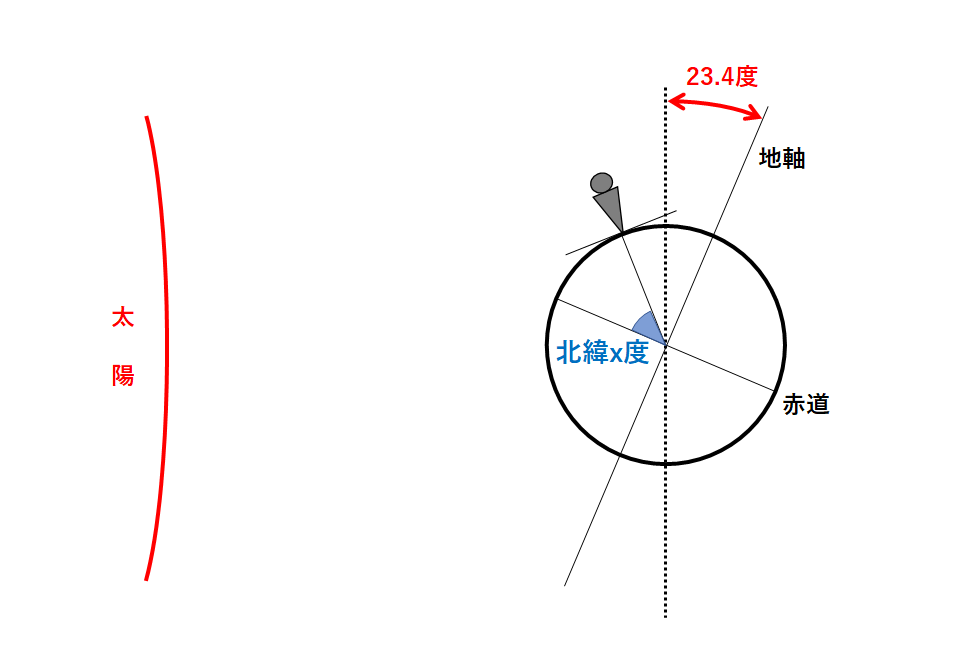
ここで春分の日の地球の位置を考えます。(↓の図)
矢印の方から地球と太陽を見てみましょう。
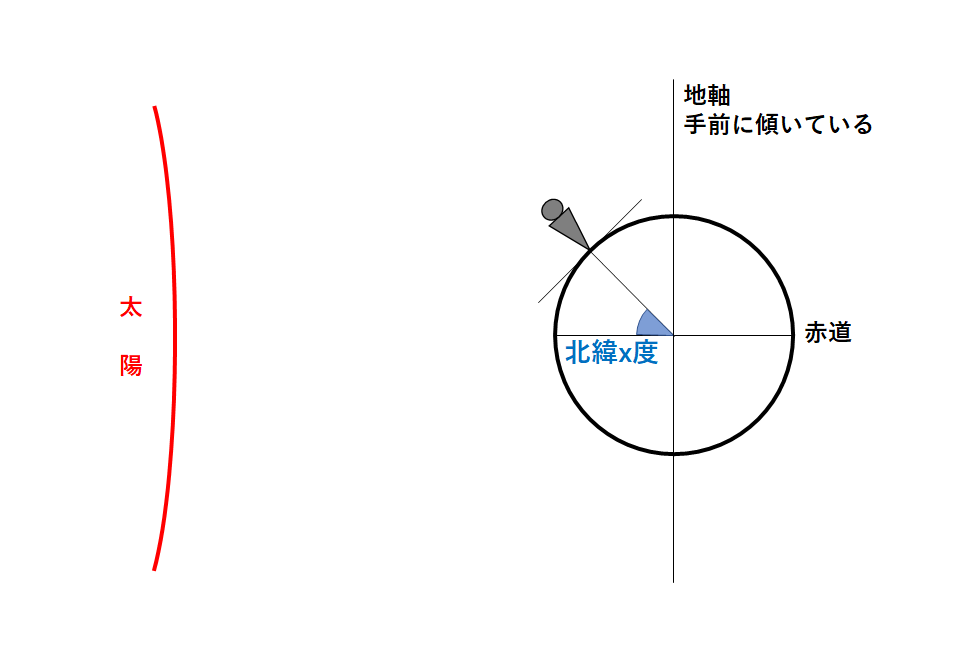
見た目ではわかりにくいですが地軸の上の部分が手前側に傾いています。
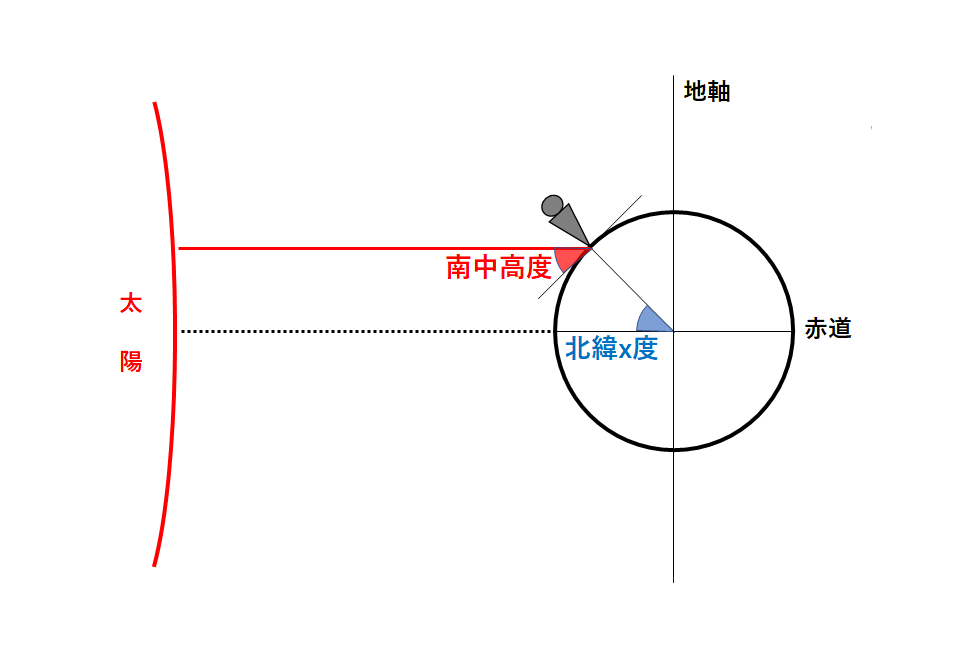
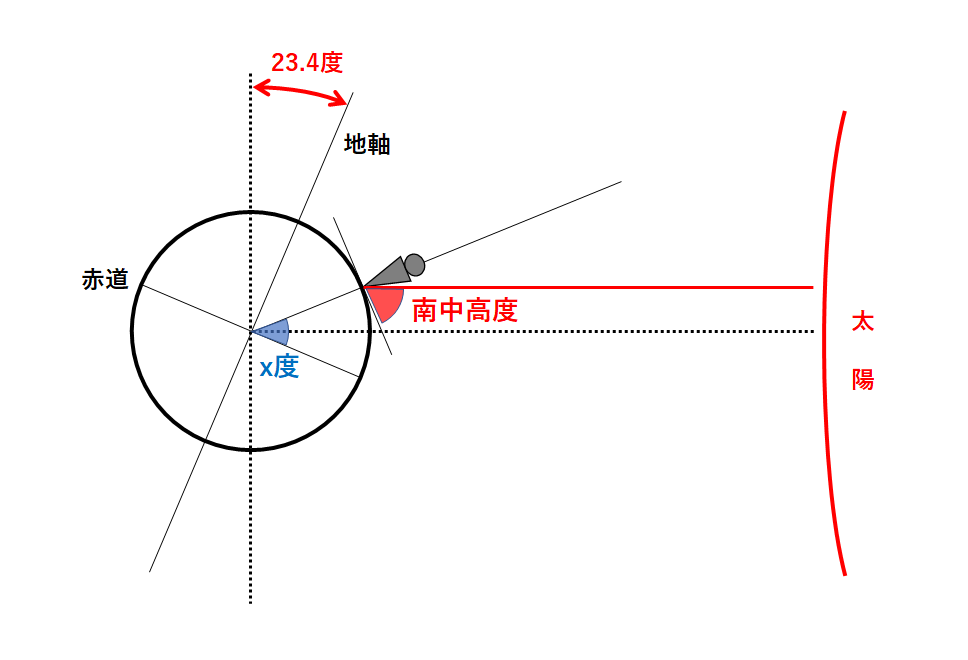
では北緯x度の地点の観測者から見たときの太陽の南中高度を考えます。(↓の図)
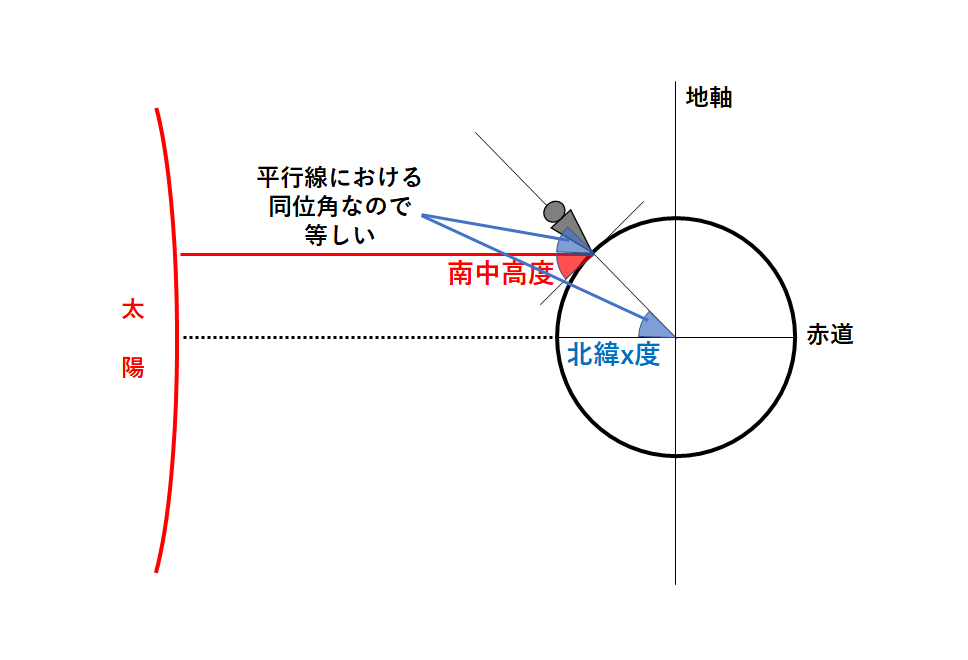
星の高度を考える場合は「平行線における同位角」を考えましょう。
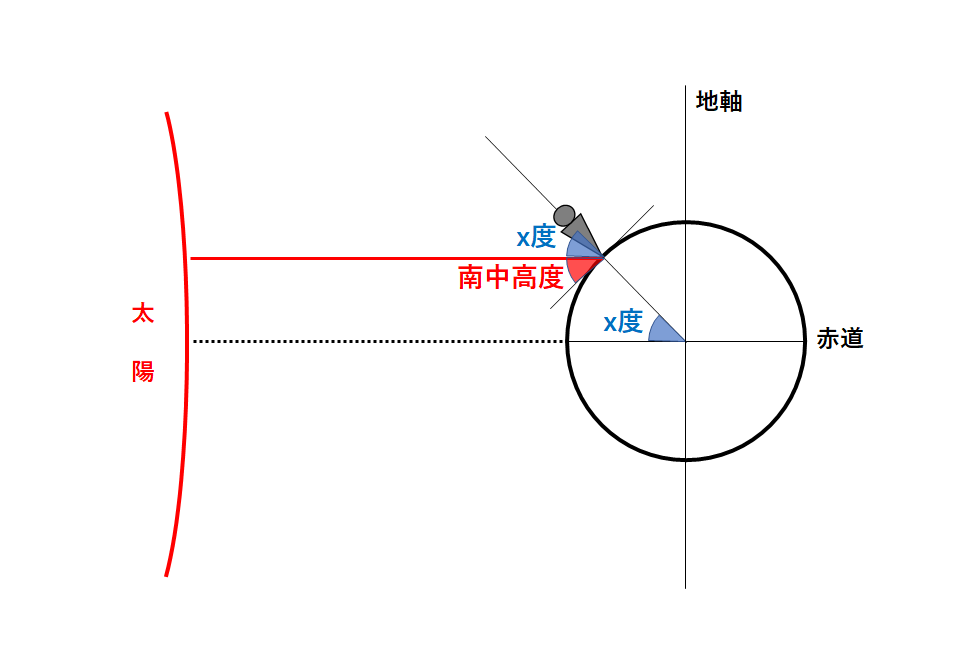
↓の図で青色の部分が同位角ですね。
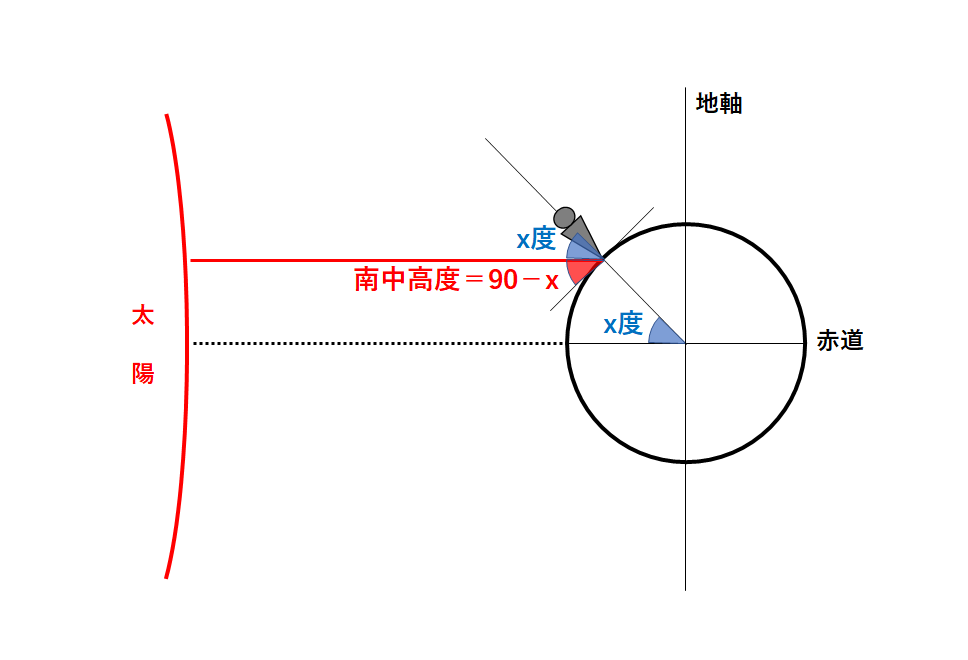
よって南中高度は「90-x」で求められますね。(↓の図)
夏至の場合
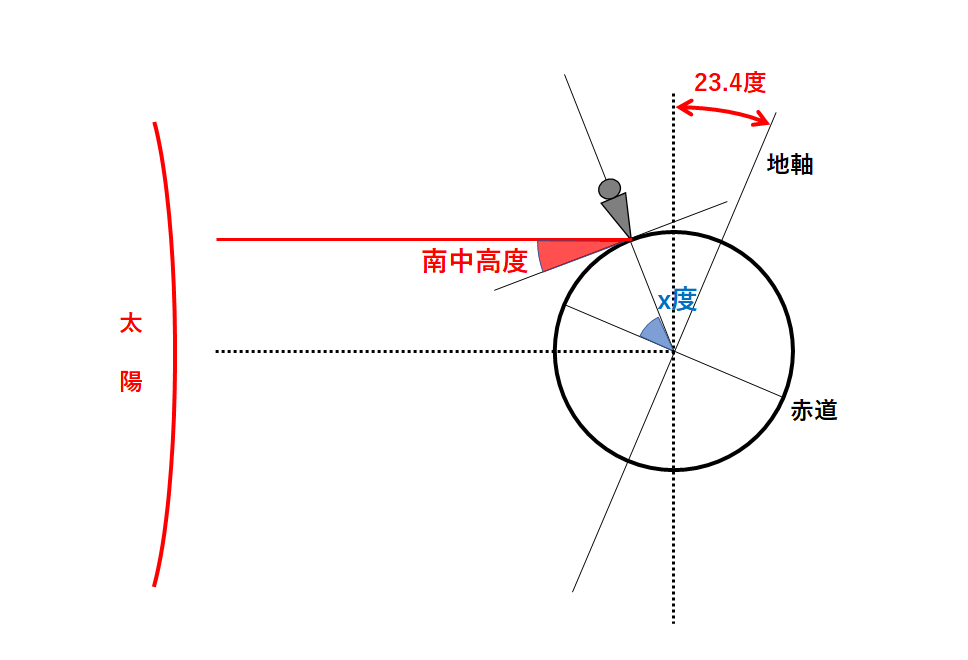
夏至の日の地球と太陽の位置は↓のようになっています。(↓の図)
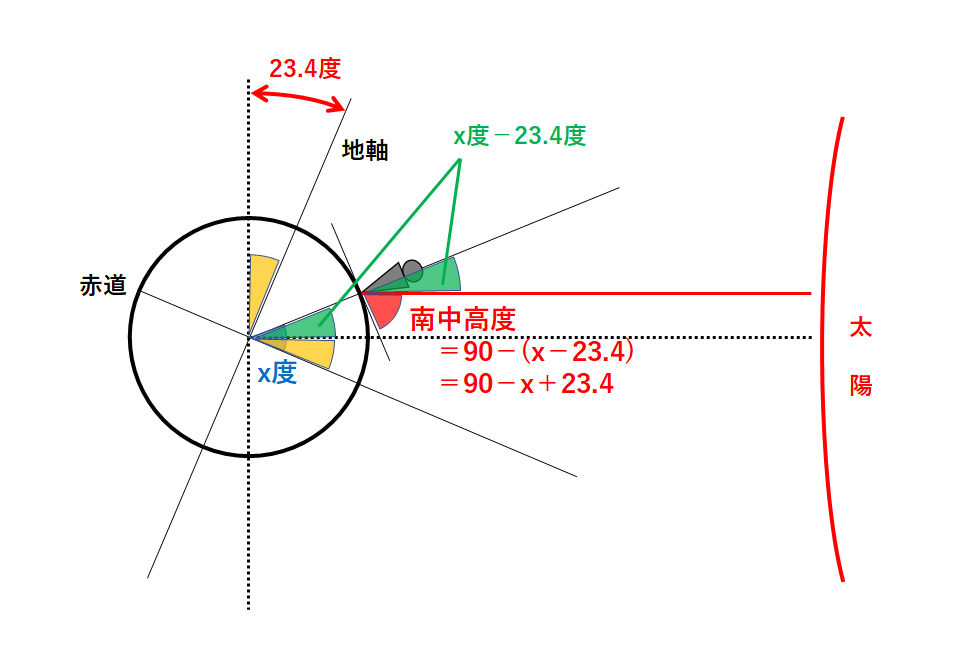
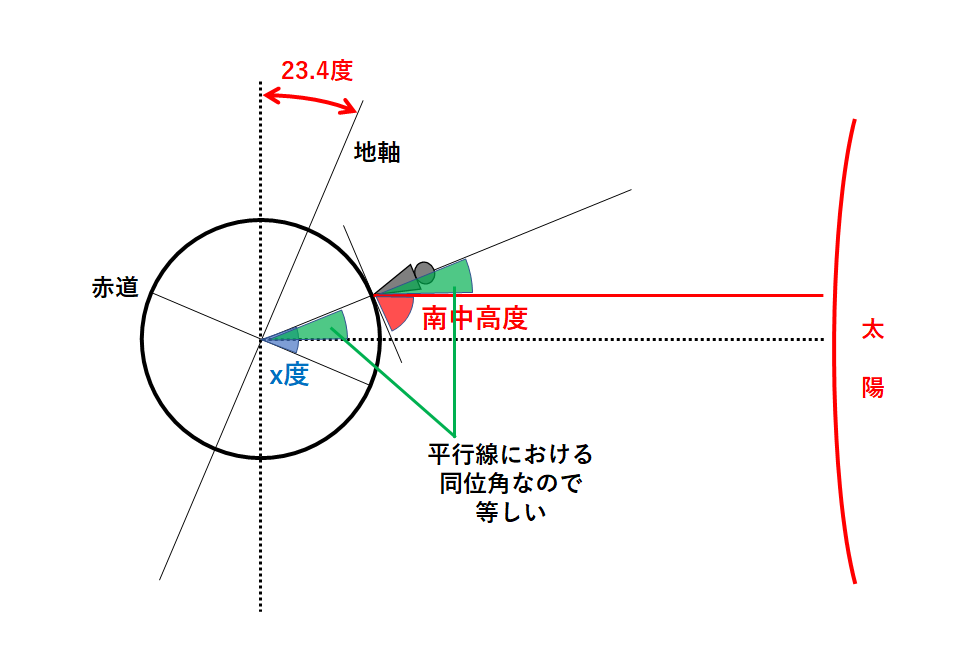
ここで北緯x度の地点の観測者から見たときの太陽の南中高度を考えます。(↓の図)
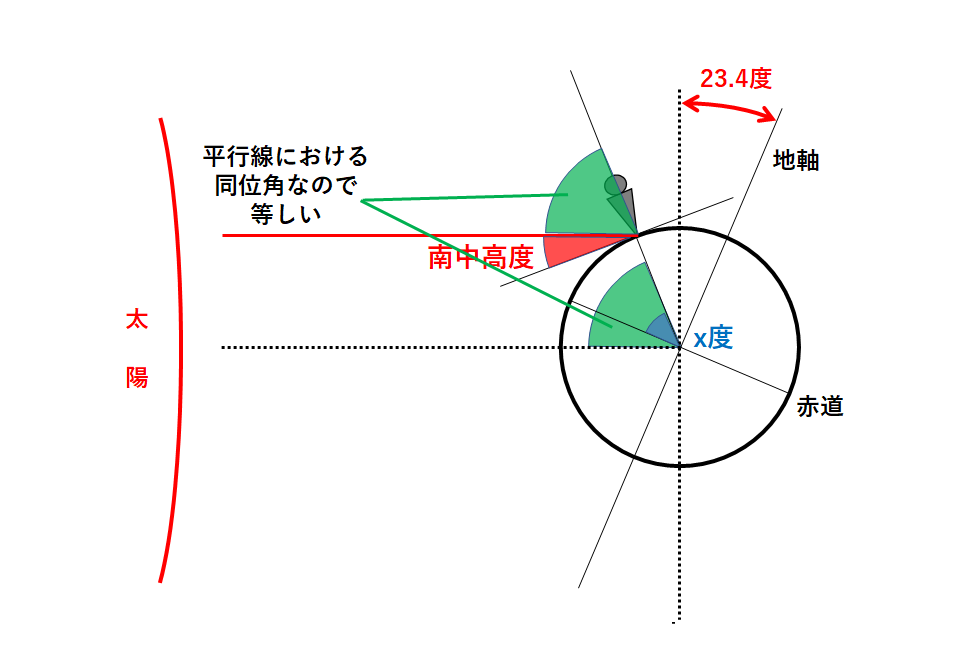
天体における角度の問題は「平行線における同位角は等しい」をやはり使います。
「同位角」は・・・(↓の図)
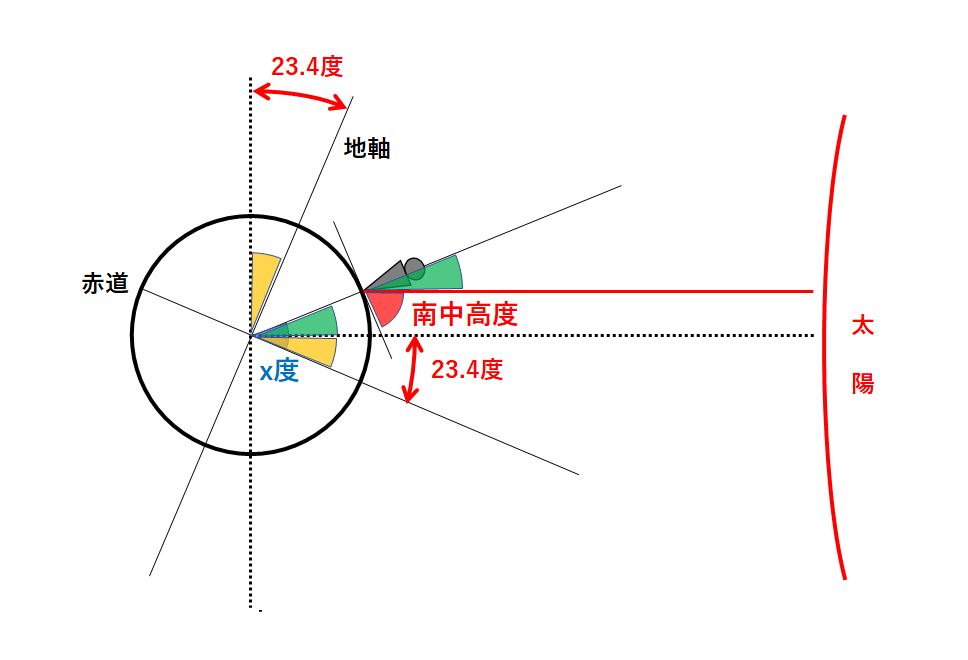
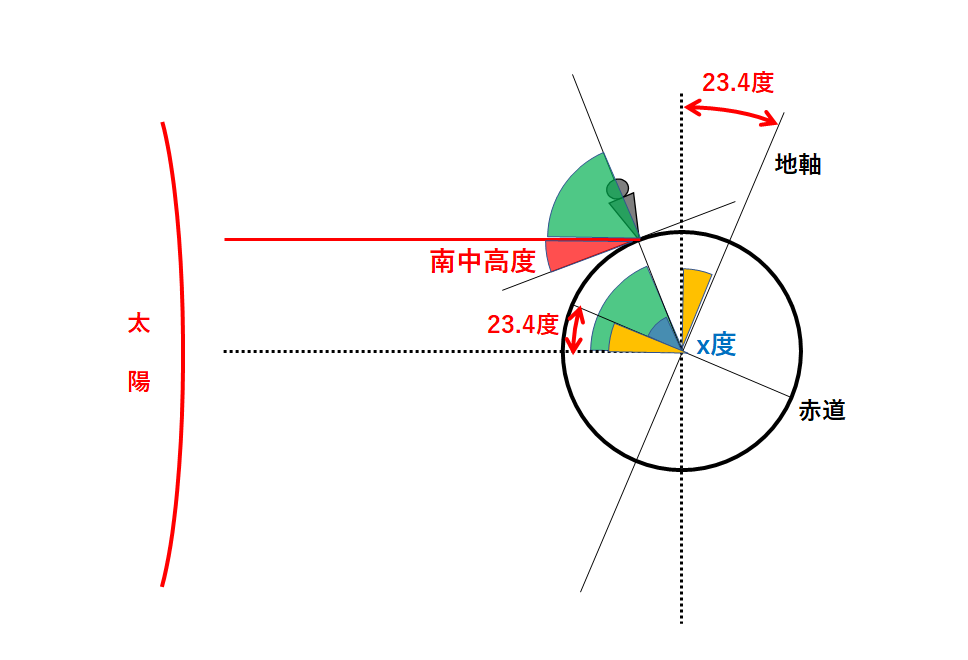
この緑色の角の大きさを求めるためには↓の黄色の角の大きさを考える必要があります。
この黄色の角は「地軸の傾き23.4度」に等しいですね。
よって緑色の角は↓のようにx-23.4度となります。
南中高度は次のようになります。
南中高度=90-(x-23.4)=90-x+23.4
よって夏至の日の太陽の南中高度は「90-x+23.4」で求められますね。
冬至の場合
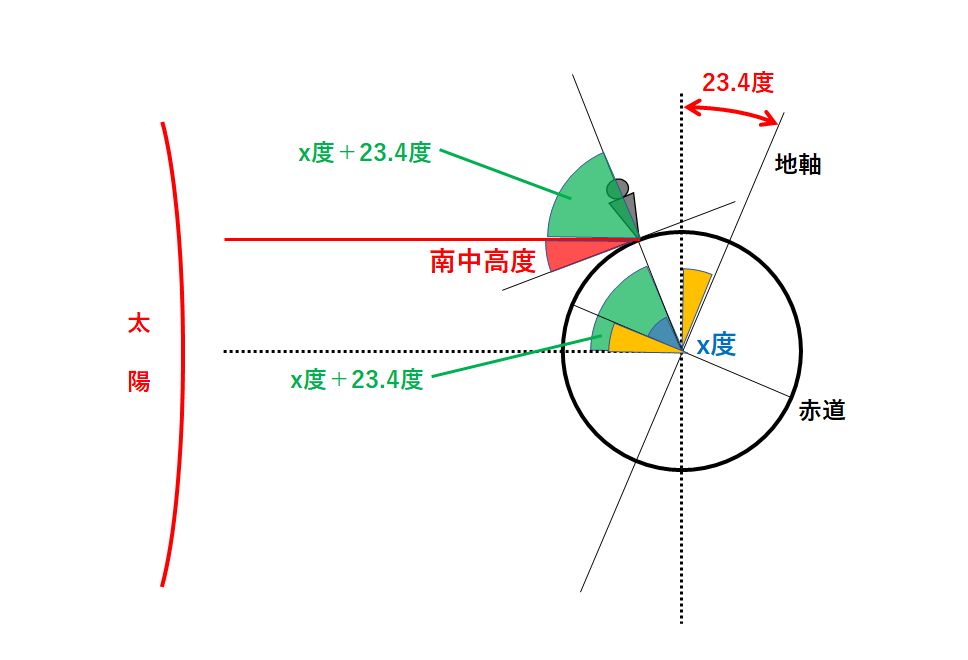
冬至の日の地球と太陽の位置関係を考えましょう。(↓の図)
ここで北緯x度の地点の観測者から見たときの太陽の南中高度を考えます。(↓の図)
ここでも「同位角」を探します。(↓の図)
この緑色の角の大きさを求めるためには
↓の黄色の角の大きさを考える必要があります。
この黄色の角は「地軸の傾き23.4度」に等しいですね。
よって緑色の角は↓のようにx+23.4度となります。
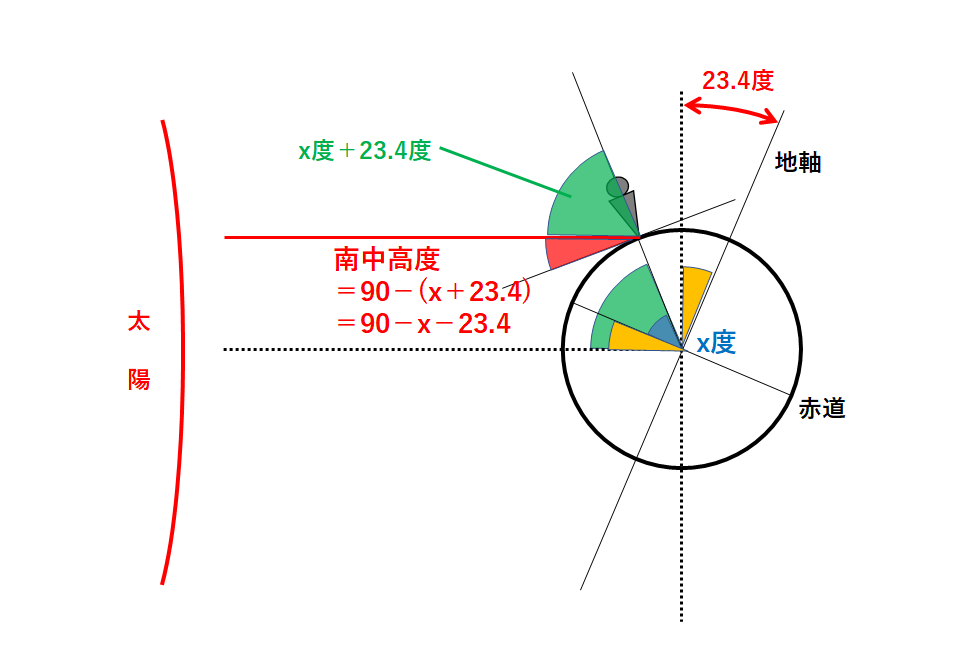
南中高度は次のようになります。
南中高度=90-(x+23.4)=90-x-23.4
したがって冬至の日の太陽の南中高度は「90-x-23.4」で求められますね。
POINT!!
・南中高度の公式を覚えよう。(できれば南半球も覚えておくとよいですよ)
・南中高度や星の高度を求めるには「平行線における同位角は等しい」ことを利用しよう!


コメント(承認された場合のみ表示されます)
[…] 中3地学【南中高度の公式】 […]
[…] 画像出典:https://chuugakurika.com/2017/12/06/post-951/ […]
南中高度って真南に来た時の高度を角度で表したものですよね?太陽と地球を上から見た図で表しているから、観測者の真上が真南になり、真下である地球の真ん中が真北になるため、南中高度は観測者の真南の90度にはならないんですか?
ねるたねるた様
コメントありがとうございます。
南北の関係は↓のようになっています。
一番上の公式の部分 冬至と夏至の公式逆じゃないですか?
通りすがりの理科好き様
コメントありがとうございます。
どの部分が逆でしょうか?
わかりやすい説明、ありがとうございます
受験生のため助かりましたm(*_ _)m
あややん様
コメントありがとうございます。
わかりやすいと言っていただけてとてもうれしいです。
またぜひご活用ください。