中3物理【*ばねの発展問題】

*このページは発展的な内容を含みます。

1．ばねにはたらく力

この単元を理解するには、ばねにはたらく力について正確に理解しておかなければなりません。

そのためには、

→【力のつり合い】←と→【作用・反作用の法則】←を理解する必要があります。

まだ理解していないという人はここから読み始めてくださいね。

では次のような例を考えてみましょう。

例

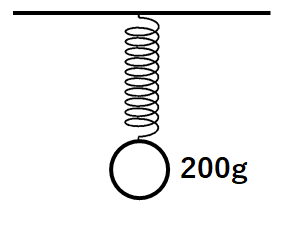
↓の図のように天井にばねをつるし、200gのおもりをつるします。

※ばねの質量は考えないものとします。

ここで天井・ばね・おもりをバラバラにしてみましょう。(↓の図)

天井・ばね・おもりは静止しています。

つまりそれぞれにはたらく力はつりあっています。

100gの物体にはたらく重力を1Nとすると、おもりにはたらく重力は2N。

矢印で表すと↓の①の力のようになります。

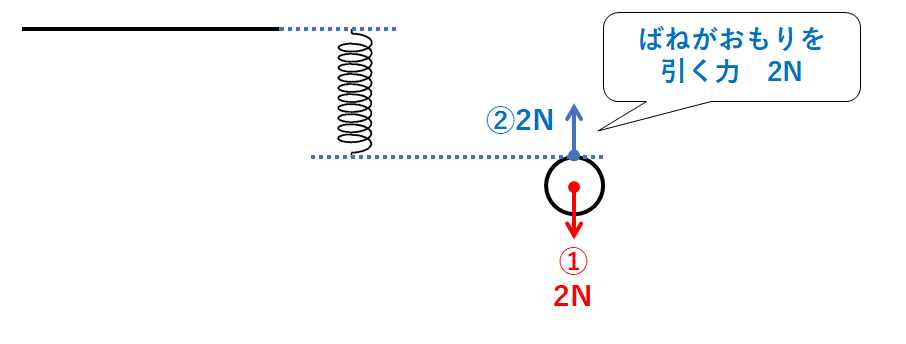
おもりには重力①がはたらいています。

おもりが動かず静止しているということは、重力①とつりあう力があるはずです。

おもりはばねと接しているので「ばねがおもりを引く力」がはたらきます。(↓の図の②)

これが重力とつりあう力です。

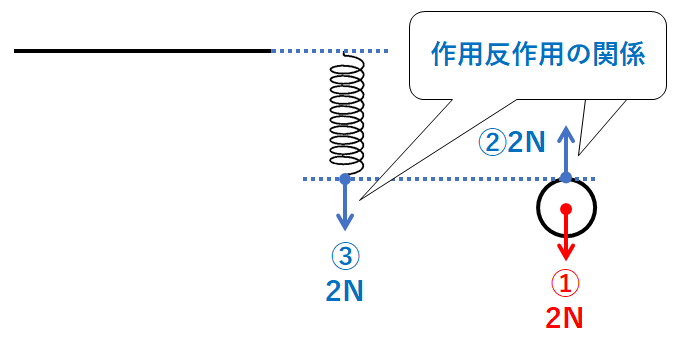
次に作用・反作用の法則を思い出しましょう。

力②には反作用があります。

作用・反作用の関係の2力は、作用点は同じ・向きは反対になっています。

つまり力②と反作用の関係にあるのは↓の図の力③です。(おもりがばねを引く力)

ばねには力③がはたらいています。

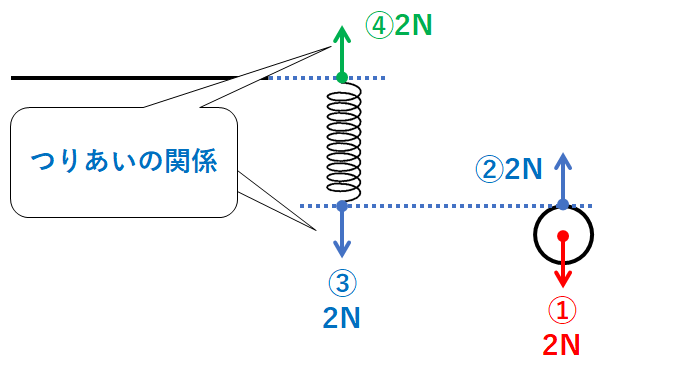
ばねは動かず静止しているので、力③とつりあう力があるはずです。

ばねは天井と接しているので「天井がばねを引く力」がはたらきます。(↓の図の力④)

これが力③とつりあう力です。

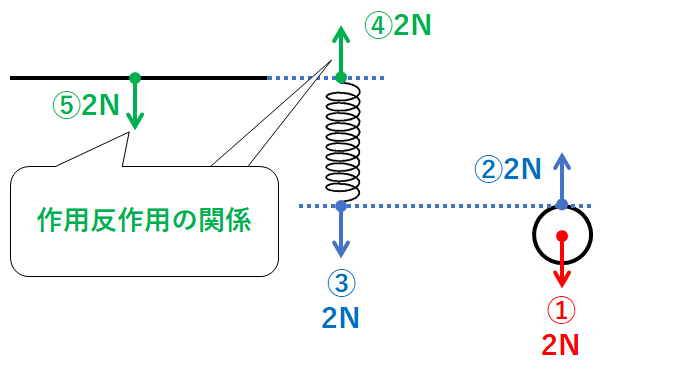
そして作用・反作用の法則。

力④の反作用があります。

作用・反作用の関係の2力は、作用点は同じ・向きは反対です。

つまり力④と反作用の関係にあるのは↓の図の力⑤です。(ばねが天井を引く力)

これで天井・ばね・おもりにはたらく力をすべて図示できました。

ここでばねにはたらく力のみに注目(↓の図)。

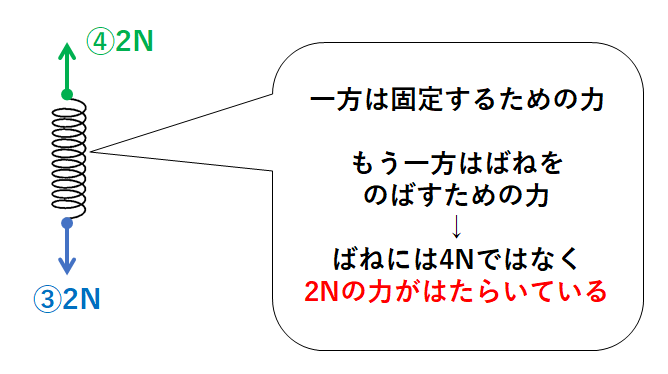
ばねには③④の2つの力があります。

しかしばねに2N＋2N＝4Nの力がはたらいていると考えてはいけません。

③④のうち

・一方は、ばねを固定しておくための力

・もう一方は、ばねをのばすための力

としてはたらくのです。

つまりばねには2Nの力がはたらいているのです。

2．ばねの発展的な問題

ここでは発展的な問題を紹介します。

よく出題されるのは、ばねの一端を天井などに固定している問題です。

しかしばねの両端が固定されている（床と天井の両方に固定）問題も存在するのです。

例題1

あるばねA、ばねBに加わる力とその長さとの関係を調べたところ、次のグラフのようになった。

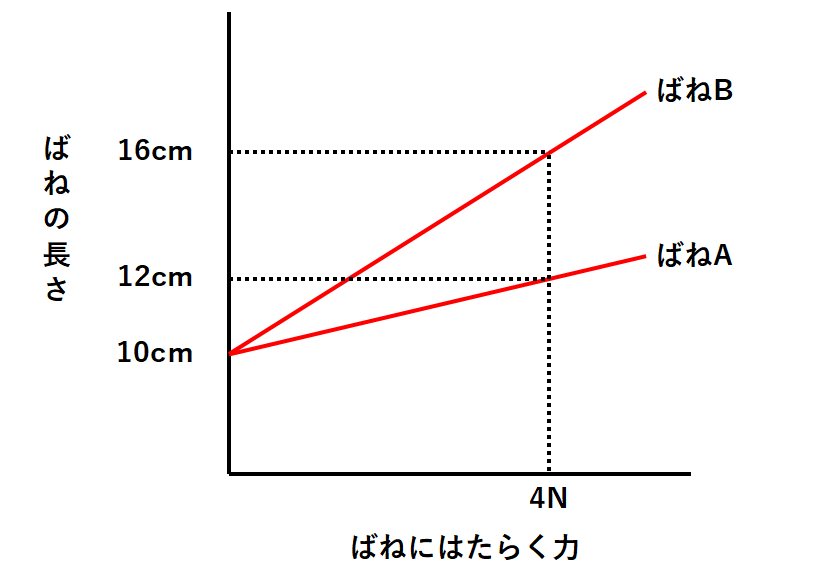
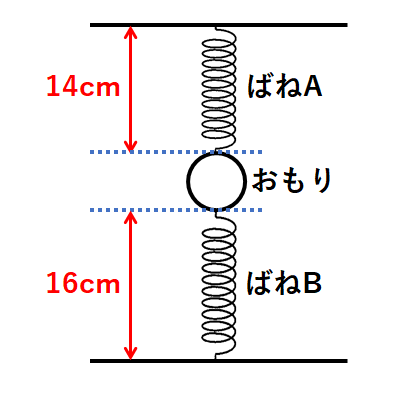
このばねA、ばねBとある質量のおもりを次の図のようにつるした。

このときばねA、ばねBの長さは図のようになった。

おもりの質量を求めよ。

ただし100gの物体にはたらく重力を1Nとし、ばねの質量は考えないものとする。

(答)

まずばねA、Bの性質を調べておきましょう。

性質とは次の2つです。

・ばねの自然長　　　・○Nで△cmのびる

ばねA
・自然長10cm　　　・4Nで2cmのびる

ばねB
・自然長10cm　　　・4Nで6cmのびる

この性質とばねA・Bの長さから、ばねA・Bにはたらく力がわかります。(↓の図)

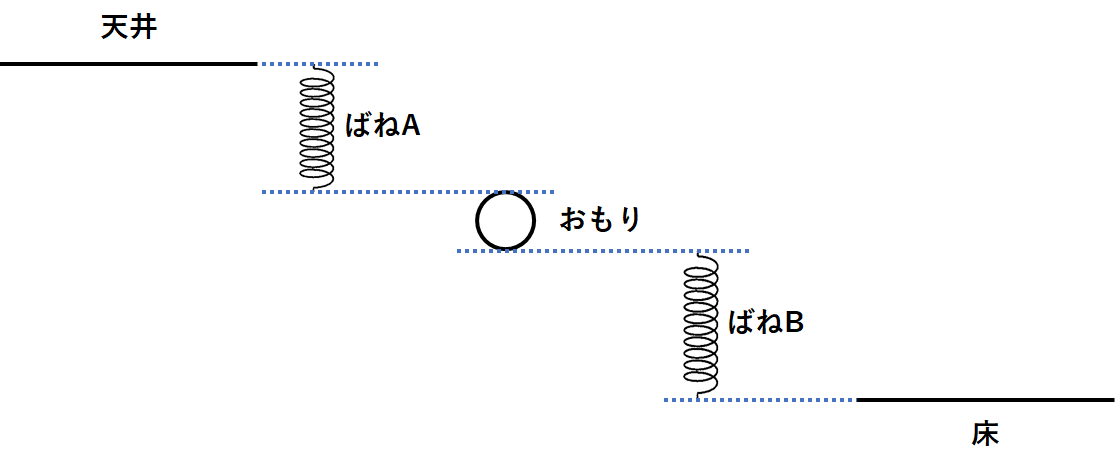
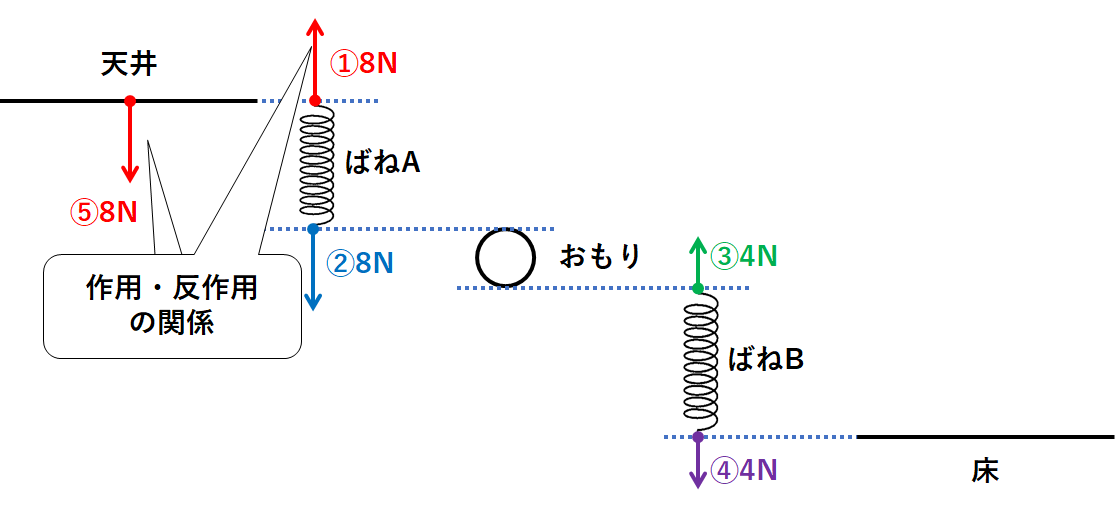
ではこの図の天井・ばねA・おもり・ばねB・床をバラバラに書きましょう。(↓の図)

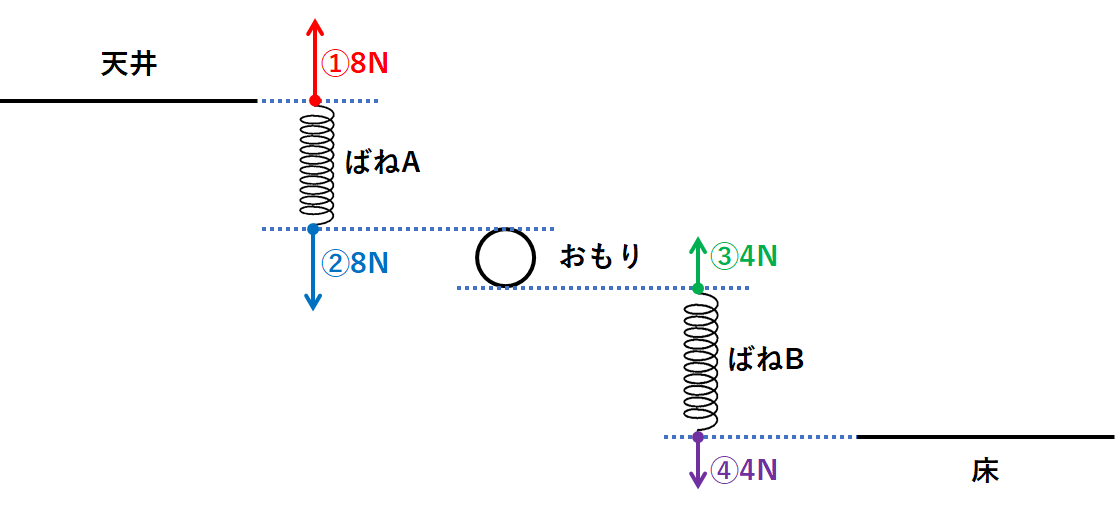
ばねAに8N・ばねBに4N　の力がはたらいていました。

図に書き込みましょう。(↓の図の①～④)

では力①の反作用を考えましょう。(ばねAが天井を引く力のこと)

↓の図の力⑤のようになります。

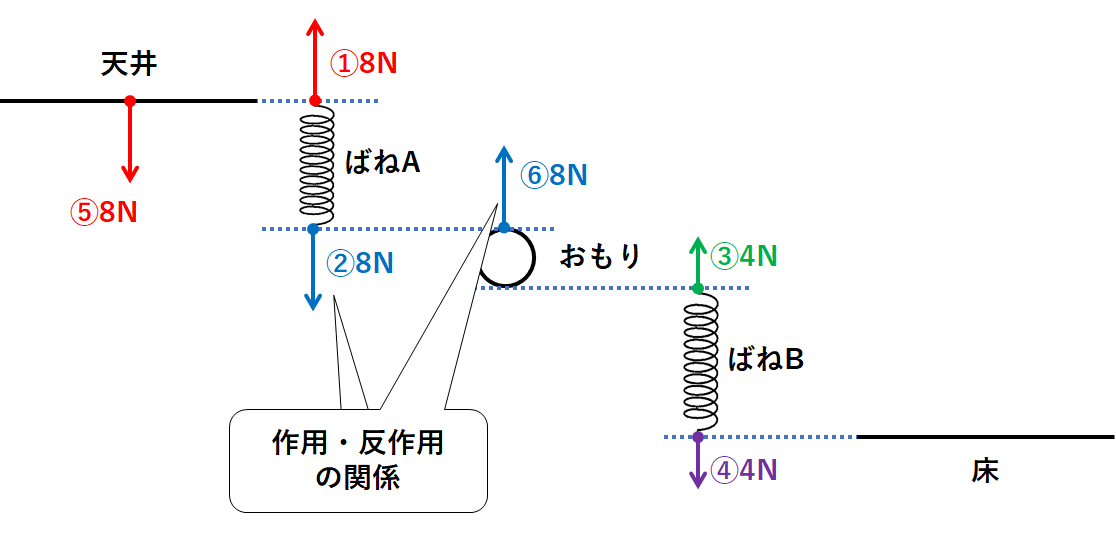
次に力②の反作用を考えましょう。(ばねAがおもりを引く力のこと)

↓の図の力⑥のようになります。

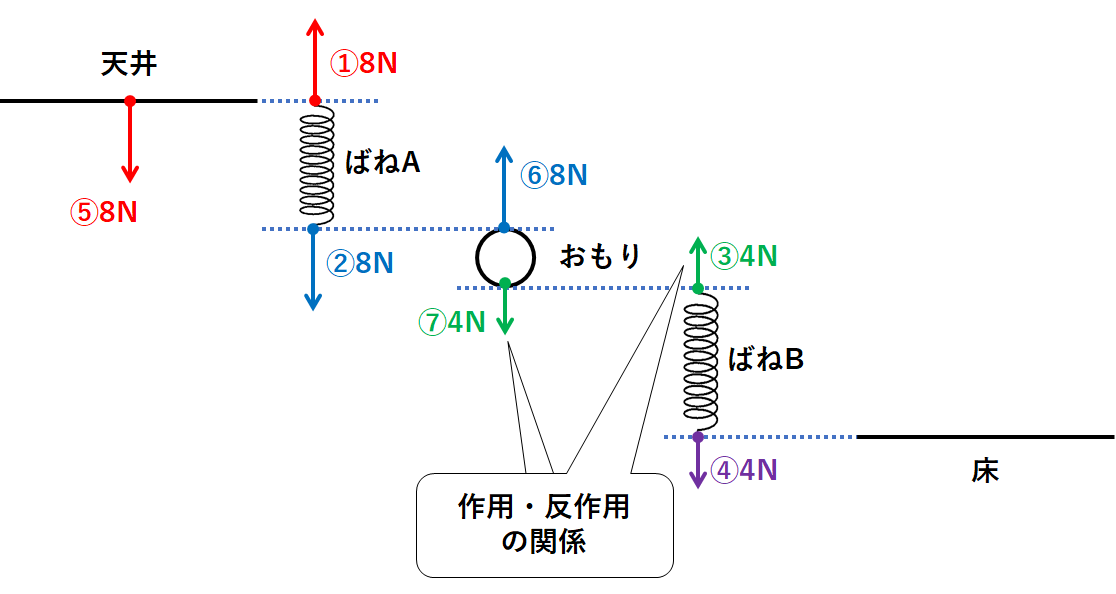
さらに力③の反作用を考えましょう。(ばねBがおもりを引く力のこと)

↓の図の力⑦のようになります。

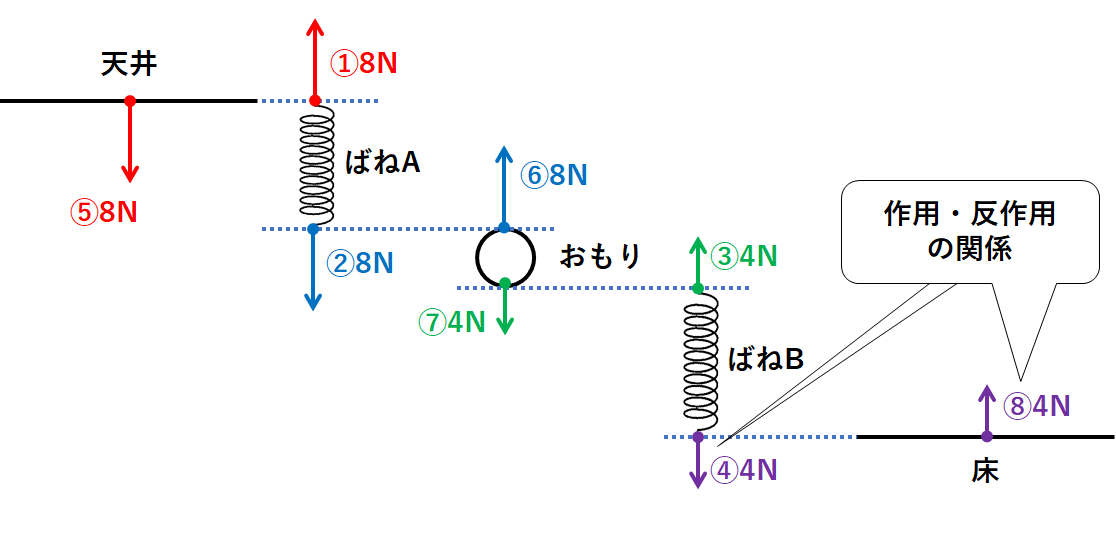
最後に力④の反作用を考えましょう。(ばねBがおもりを引く力のこと)

↓の図の力⑧のようになります。

いま求めなければいけないのはおもりの質量です。

おもりの部分に注目しましょう。(↓の図)

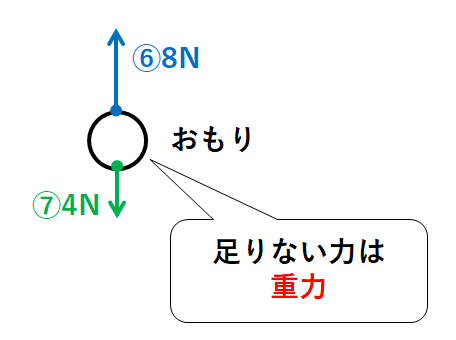
力⑥と力⑦の力だけではつりあいません。(おもりは静止しない)

何か力が足りないのです。

おもりの重力が足りませんね。

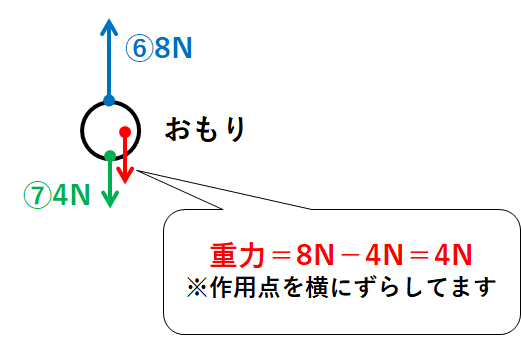
力⑥と力⑦とおもりの重力のつり合いを考えて

おもりの重力＝8N－4N＝4N

となります。(↓の図)

よっておもりの質量は400gとなります。

例題2

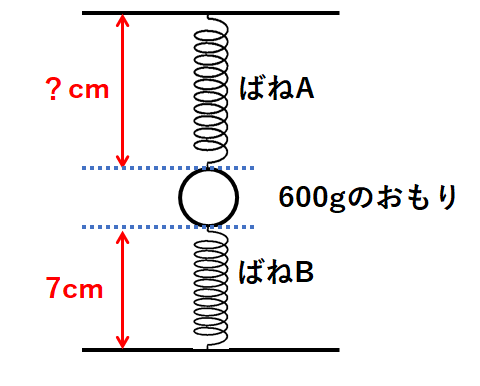
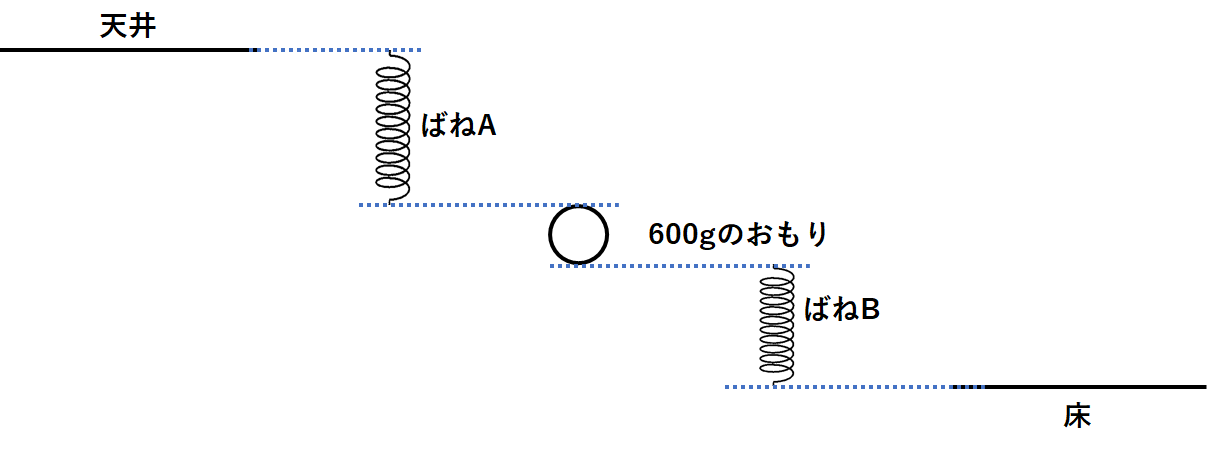
例題1のばねA、ばねB、600gのおもりを次の図のようにつないだ。

このときばねAののびは何cmか。

(答)

まずばねA、Bの性質は次のようになっていました。

ばねA
・自然長10cm　　　・4Nで2cmのびる

ばねB
・自然長10cm　　　・4Nで6cmのびる

ばねBは自然長10cmよりも短い長さになっています。

つまりばねBは3cm縮んでいることになります。

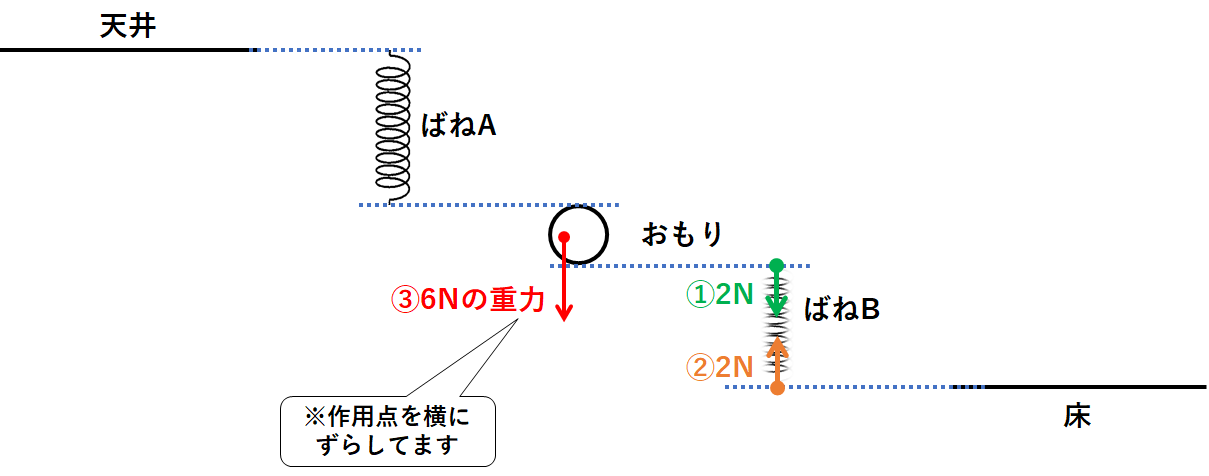
よってばねBには2Nの縮める力がはたらいています。(↓の図)

縮む向きであることに注意しましょう。

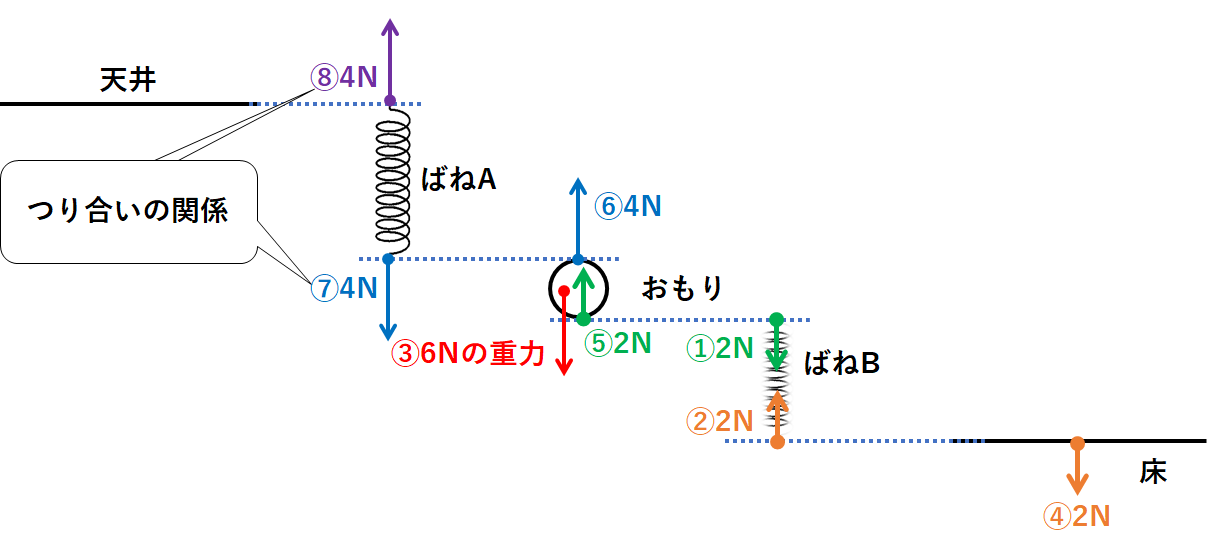
次に天井・ばねA・おもり・ばねB・床をバラバラにしてみましょう。(↓の図)

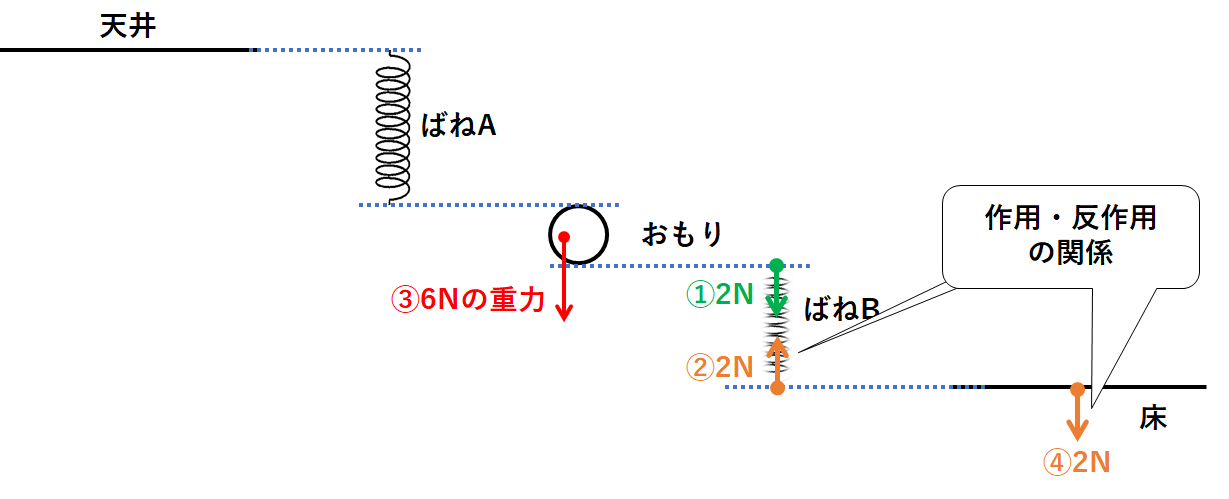
ここにばねBを縮める力①・力②、おもりの重力③を書きます。(↓の図)

力②の反作用の力を考えましょう。(ばねBが床を押す力のこと)

↓の図の力④のようになります。

次に力①の反作用の力を考えましょう。(ばねBがおもりを押す力のこと)

↓の図の力⑤のようになります。

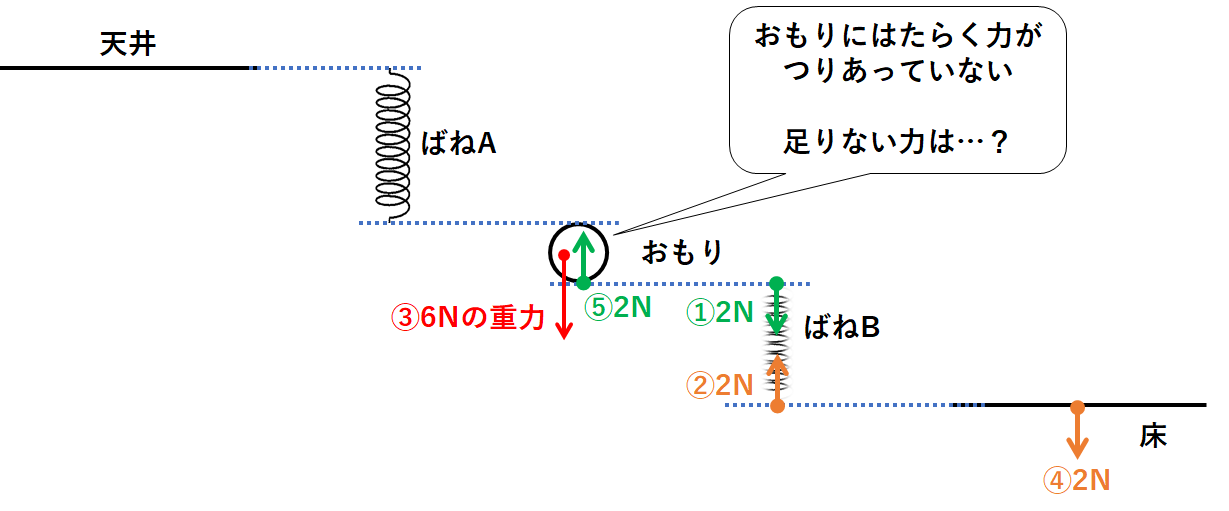
ここでおもりにはたらく力③・力⑤に注目しましょう。

力③と力⑤だけではつりあいません。

足りない力は上向き4Nの力です。(↓の図)

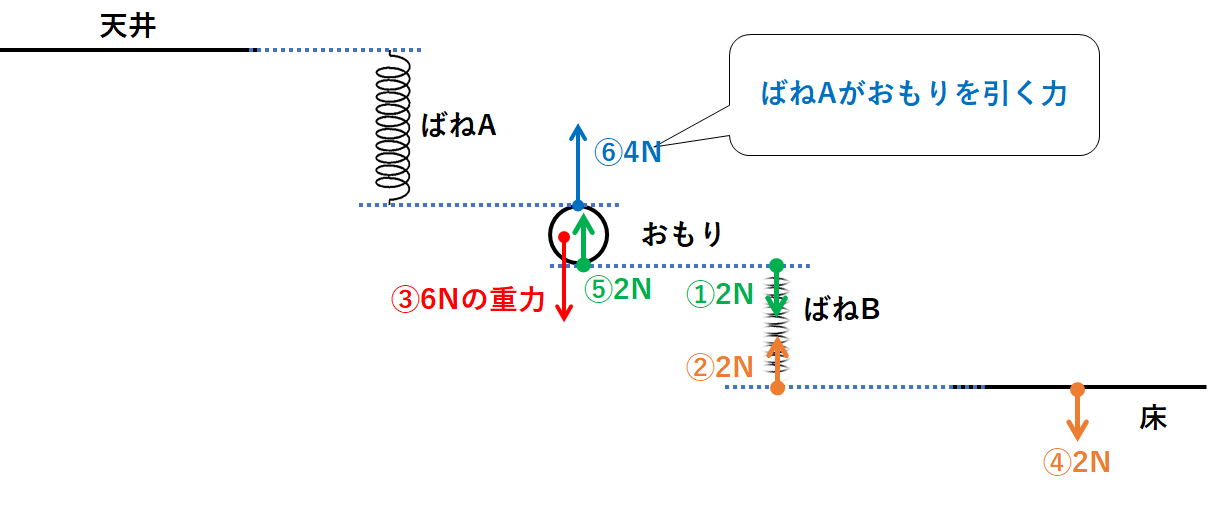
つまりばねAがおもりを上向き4Nで引いていると考えられます。(↓の図の力⑥)

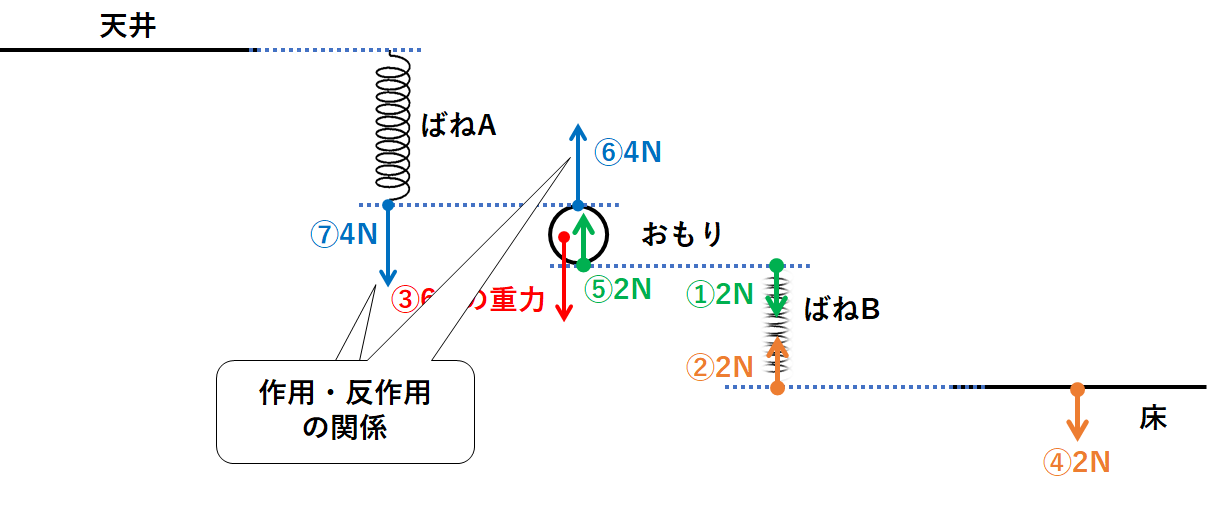
力⑥の反作用の力を考えましょう。(おもりがばねAを引く力のこと)

↓の図の力⑦のようになります。

ばねAに注目します。

力⑦だけが書かれていますが、このままではつりあいません。

足りない力は上向き4Nの力です。

つまり天井がばねAを引く力が↓の図の力⑧のように存在します。

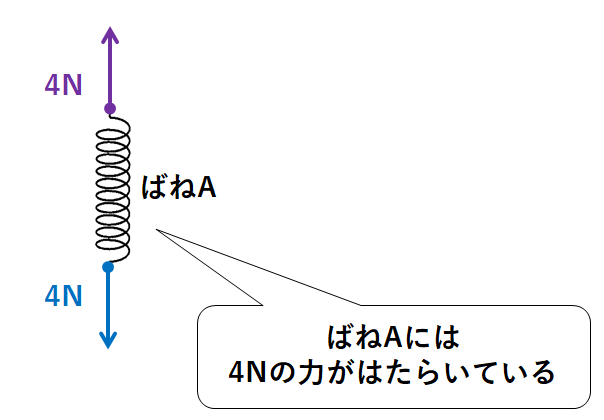
よってばねAにはたらく力は↓の図のようになっているので

ばねAには4Nの力がはたらきます。

（ばねに両端から力がはたらいているとき、一方の力がのばす力としてはたらく。）

そしてばねAは4Nで2cmのびるばねでした。

よってばねAののびは2cmとなります。