このページでは「てこ」を使った仕事について解説しています。
仕事の基本については→【仕事とは】←を参考に。
※てこの部分に関する動画は↓↓↓
チャンネル登録はこちらから↓↓↓
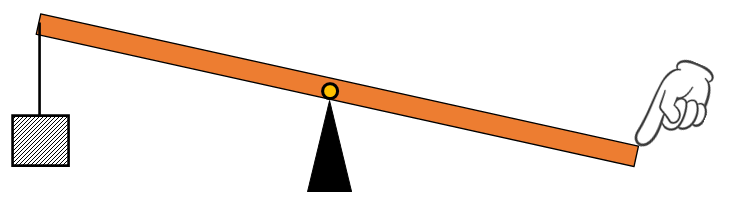
1．“てこ”とは
“てこ”とは↓のような道具です。
片方におもりをつり下げたり、のせたりします。
そしてもう一方に力を加えて、おもりを持ち上げます。
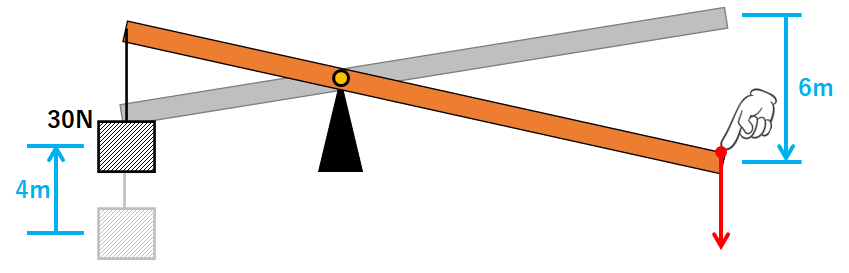
出題例①
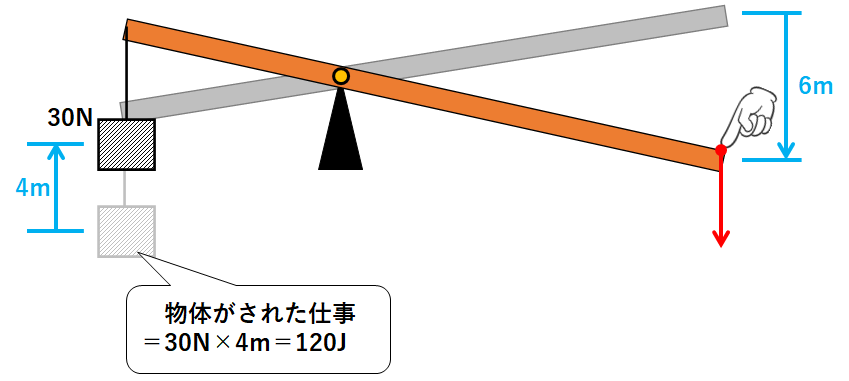
↓のように、30Nのおもりを4m持ち上げるために、てこの右端を6m押し下げます。
このとき、おもりがされた仕事は「30Nのおもりを4m持ち上げるための仕事」なので
おもりがされた仕事(J)＝力(N)×力の向きに動かす距離＝30N×4m＝120J
となります。(↓の図)
※もう1つの考え方
この場合、おもりにした仕事は、おもりの位置エネルギーへと変化します。
つまり
おもりがされた仕事(J)＝おもりが得た位置エネルギー(J)
ということができます。
その考え方をして
おもりがされた仕事(J)＝おもりが得た位置エネルギー(J)＝重さ(N)×高さ(m)＝30N×4m＝120J
と求めることもできます。
おもりがされた仕事＝120Jであるので、人がした仕事も120Jということができます。・・・(＊)
一方で、人はてこの右端を6m押し下げています。
てこの右端に加えた力はわかっていませんので、x(N)とすると
人がした仕事(J)＝力(N)×力の向きに動かした距離(m)＝x(N)×6m＝6x(J)
となります。(↓の図)
(＊)より、これは120Jと等しいので次の式が成り立ちます。
6x＝120
これを解くとx＝20Nとなり、人がてこの右端に加えた力は20Nとわかります。
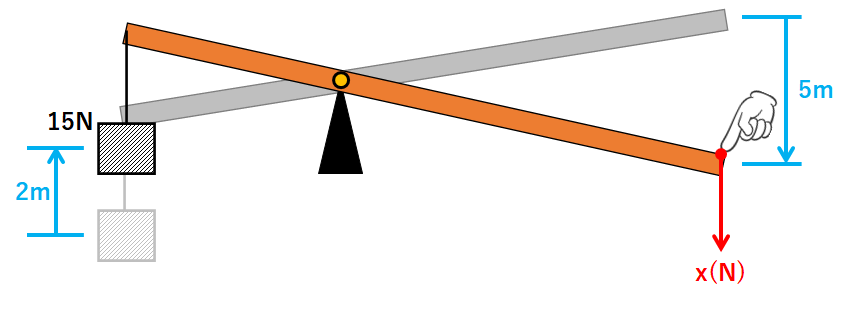
例題1
↓のように15Nのおもりを2m持ち上げた。このとき人は、てこの右端を5m押し下げた。
人がてこの右端を押した力x(N)はいくらか。
(答)
物体がされた仕事＝15N×2m＝30J
人がした仕事＝x(N)×5m＝5x(J)
これらは等しいので
5x＝30
これを解いてx＝6Nとなります。
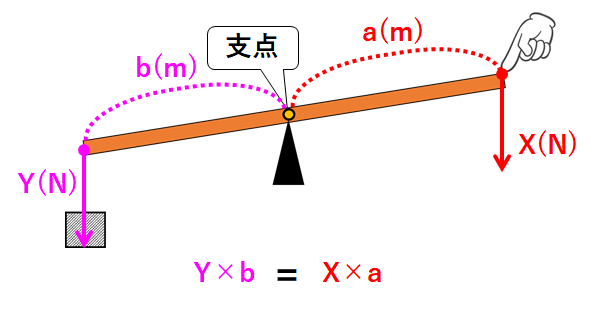
2．てこの原理
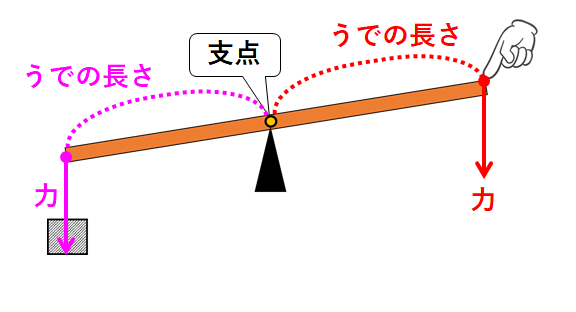
てこが支えられている点を支点といいます。
また、支点から力のはたらく点までの距離をうでの長さといいます。
てこにおいては次が成り立ちます。
力×うでの長さ＝一定 である。
例えば↓の図において次の式が成り立つ。
X(N)×a(m)＝Y(N)×b(m)
これをてこの原理という。
出題例②
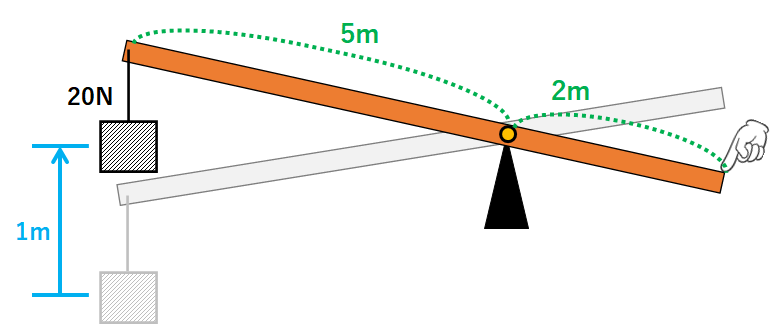
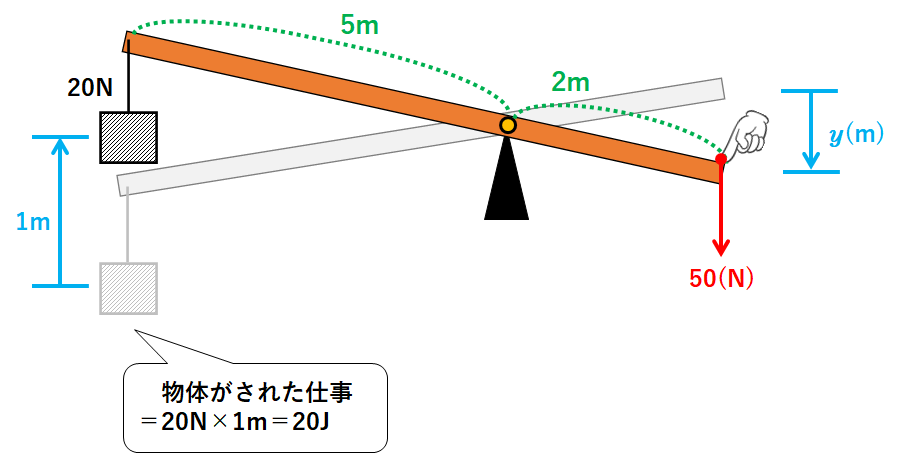
↓のように20Nのおもりを1m持ち上げます。このときてこの右端を押し下げます。
このとき、人はてこを何m押し下げたでしょうか？
てこの原理を使います。
人が押した力をx(N)とします。
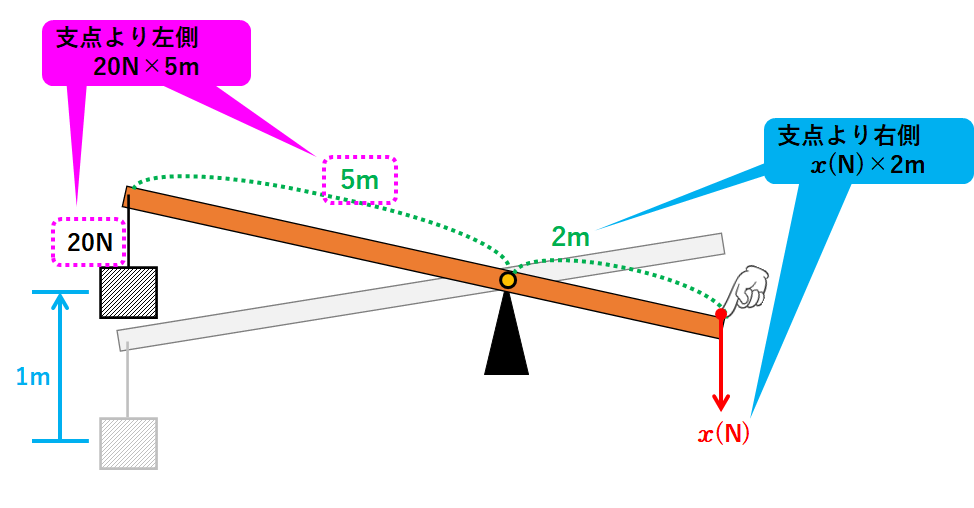
支点から左側をみると
力×うでの長さ＝20N×5m
支点から右側をみると
力×うでの長さ＝x(N)×2m (↓の図)
これらは等しいので
20N×5m＝x(N)×2m
これを解いてx＝50N
人がてこの右端を押した力は50Nとわかります。
ここからは先ほどと同様です。
物体がされた仕事＝20N×1m＝20J (↓の図)
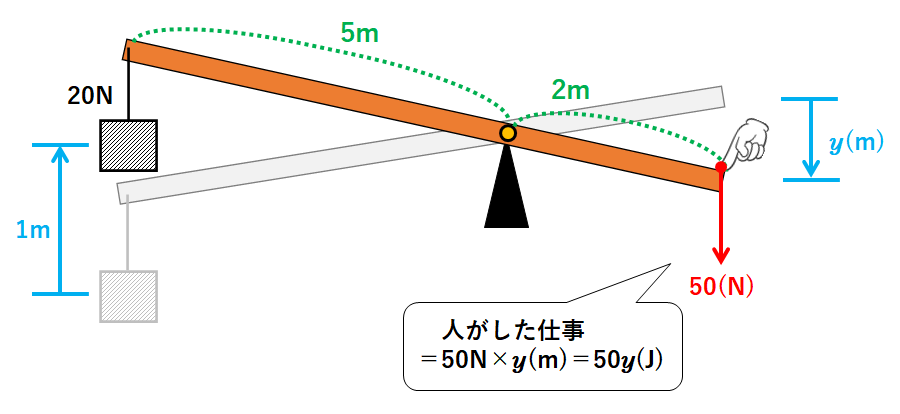
人が押し下げた距離をy(m)とすると
人がした仕事＝50N×y(m)＝50y(J) (↓の図)
これらは等しいので
50y＝20
これを解いてy＝0.4m
よって人が右端を押し下げた距離は0.4mとわかります。
例題2
(1)人がてこの右端を押した力は何Nか。
(2)人がてこの右端を押した距離は何mか。
(答)
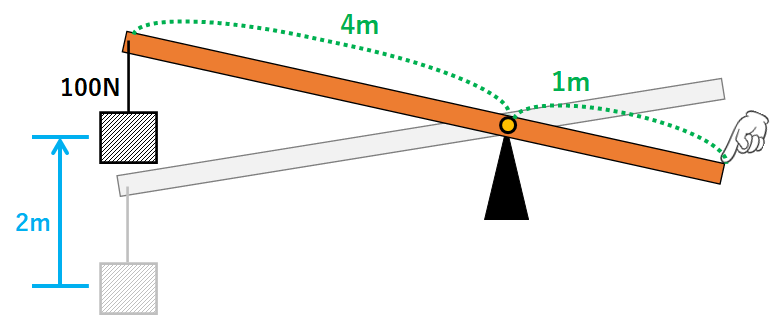
(1)
『力×うでの長さ＝一定』であるので、人が押した力をx(N)とすると
100N×4m＝x(N)×1m
これを解いてx＝400N
人が押した力は400Nとなります。
(2)
物体がされた仕事＝100N×2m＝200J
人が押した距離をy(m)とすると
人がした仕事＝400N×y(m)＝400y(J) ※200Nは(1)の答えから
これらは等しいので
400y＝200
これを解いてy＝0.5m
よって人が押した距離は0.5mとなります。
コメント(承認された場合のみ表示されます)