中1化学【溶解度の計算問題】

1．溶解度に関する計算

溶解度に関する計算問題はバリエーションが非常に多いため、解法パターンの暗記では到底追いつきません。

 

 

 

しかし最低限覚えておくべき解法というのもあります。

 

 

 

ここではそれを紹介したいと思います。

 

 

 

以下の例題ではすべて溶質をXという物質であるとし、各温度における水100gに溶ける量（溶解度）が↓の表のようになっているとします。

 

 

例題1

60℃の水にXを溶けるだけ溶かし、飽和水溶液をつくった。質量パーセント濃度はいくらか。
小数第2位を四捨五入して答えよ。

 

---

(答)
水の量が指定されていません。

 

 

 

じゃあ求められないのか？というとそうではありません。

 

 

 

この場合は水の量を100gと仮定して解きましょう。

 

 

 

ちなみに

$$質量パーセント濃度＝\frac{溶質(g)}{水溶液全体(g)}×100$$

で求められます。

 

 

 

60℃の水100gにはXが130gが溶けるので

$$\frac{130g}{100g+130g}×100=\frac{130}{230}×100＝56.52・・・=56.5％$$

となります。

 

 

 

よって56.5％が正解です。

 

 

 

しかし水の量を勝手に100gにしたけれど、200gなら違うんじゃないの？と思う人もいるかもしれません。

 

 

 

もし水200gだったら、と仮定して計算してみましょう。

 

 

 

60℃の水200gにはXが260gが溶けるので

$$\frac{260g}{200g+260g}×100=\frac{260}{460}×100=\frac{130}{230}×100=56.52・・・=56.5％$$

と結局同じ計算をすることになります。

 

 

 

つまり飽和水溶液の濃度は水の量に関係なく（温度によって）一定となっています。

 

 

 

例題2

30℃の水にXを溶けるだけ溶かし、飽和水溶液200gをつくった。この飽和水溶液から水を50g蒸発させると何gのXが結晶として現れるか。

 

---

(答)

蒸発させた水50gに溶けていたXが結晶として現れます。

すなわち、（蒸発させる）50gの水に溶けるXの量を求めればよいのです。

 

 

 

現れる結晶の質量をx(g)とすると

$$100g:39g=50g:x(g)$$

$$x=19.5g$$

 

 

 

よって19.5gが正解です。

 

 

 

例題3

60℃の水にXを溶けるだけ溶かし、飽和水溶液230gをつくった。

(1) この中に溶けているXは何gか。

(2) この水溶液の温度を30℃まで下げたとき、生じる結晶は何gか。

 

---

(答)

(1)

できるだけきちんと状況を整理しましょう。

 

 

 

いま水の量がわかりませんが、表より

60℃の水100gにXは130gまで溶ける（60℃の飽和水溶液が230g）

ことがわかります。

 

 

 

よって飽和水溶液230gにはXは130g溶けていることがわかります。

 

 

 

 

(2)

(1)より、いまの水の量は100gです。

表より

30℃の水100gにXは39gまで溶ける

ことがわかります。

 

 

 

もともと溶けていたXは130gなので、生じる結晶は

$$130-39=91g$$

となります。

 

 

 

よって91gが正解です。

 

 

 

例題4

60℃の水にXを溶けるだけ溶かし、飽和水溶液460gをつくった。

(1)この中に溶けているXは何gか。

(2)この水溶液の温度を30℃まで下げたとき、生じる結晶は何gか。

 

---

(答)

(1)

いま水の量がわかりませんが、表より

60℃の水100gにXは130gまで溶ける（60℃の飽和水溶液が230g）

ということがわかります。

 

 

 

つまり飽和水溶液230gにはXが130g溶けているということです。

 

 

 

では飽和水溶液460gに溶けているXの量をy(g)とすると

$$230 g:130 g=460 g:y (g)$$

$$y=260g$$

（「飽和水溶液の量：溶けているXの量」という比例式）

 

 

 

よって260gが正解です。

 

 

 

(2)

(1)より水は

460－260＝200g

あることがわかります。

 

 

 

表より

30℃の水100gにXは39gまで溶ける

ことがわかります。

 

 

 

よって

30℃の水200gにはXは　39×2＝78g　まで溶ける

ことがわかります。

 

 

 

よって生じる結晶は

$$260g-78g=182g$$

となります。

 

 

 

よって182gが正解です。

 

 

 

 

ここで例題3と例題4を振り返りましょう。

 

 

 

例題3では

60℃のXの飽和水溶液230g（水：100g　X：130g）

→30℃まで下げたときの結晶は91g

 

 

 

例題4では

60℃のXの飽和水溶液460g（水：200g　X：260g）

→30℃まで下げたときの結晶は182g

となっていました。

 

 

飽和水溶液の量と生じる結晶の量が比例しています。

この関係を利用して次の例題5を見てみましょう。

 

 

 

例題5

60℃の水にXを溶けるだけ溶かし、飽和水溶液115gをつくった。
この水溶液の温度を30℃まで下げたとき、生じる結晶は何gか。

 

---

(答)

例題3や4より

60℃のXの飽和水溶液230g（水：100g　X：130g）

→30℃まで下げたときの結晶は91g

であることがわかっています。

 

 

 

求める結晶をz(g)として、

飽和水溶液の量と生じる結晶の量が比例することを利用すると

$$230g:91g=115g:z(g)$$

$$z=45.5g$$

となります。

（「飽和水溶液の量：結晶の量」という比例式）

 

 

 

つまり45.5gの結晶が生じることになります。

 

 

 

例題6

50℃の水にXを溶けるだけ溶かし、飽和水溶液100gをつくった。

この水溶液の温度を10℃まで下げたとき、生じる結晶は何gか。

小数第2位を四捨五入して答えよ。

---

(答)

まず表より

50℃の水100gにはXが90gまで溶ける（50℃の飽和水溶液190gができる）

10℃の水100gにはXが13gまで溶ける

ことがわかります。

 

 

 

この数字から50℃の飽和水溶液190gを10℃まで下げると

$$90-13=77g$$

の結晶が生じることがわかります。

 

 

 

つまり

50℃の飽和水溶液190g

→10℃まで下げると77gの結晶

ということです。

 

 

 

いまの問題では

50℃の飽和水溶液100g

→10℃まで下げると？？gの結晶

を考えさせていますね。

 

 

 

w(g)の結晶が現れるとすると

$$190g:77g=100g:w(g)$$

$$w=40.52・・・≒40.5g$$

（「飽和水溶液の量：結晶の量」という比例式）

 

 

よって40.5gの結晶が現れることがわかります。

 

 

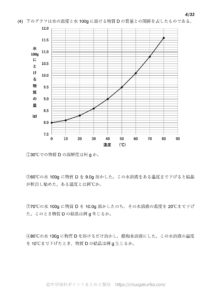
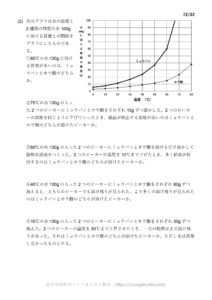
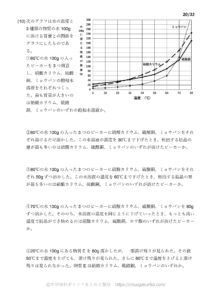
こちらもどうぞ

溶解度の計算問題をつくりました。

こちらにて販売中です。（PDFファイルのダウンロード販売です）

1ファイルで220円です。よければどうぞ。