1.電熱線の長さと抵抗の関係
ある材質Xでできた電熱線があります。
この電熱線は
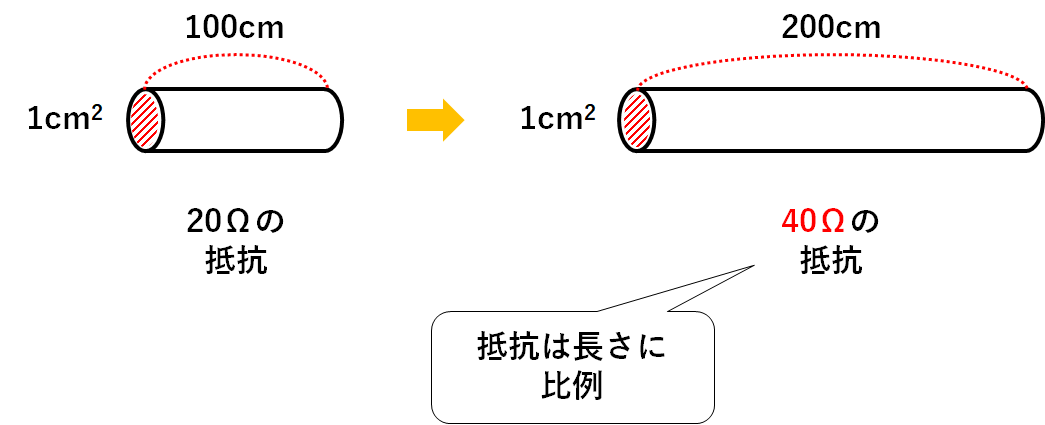
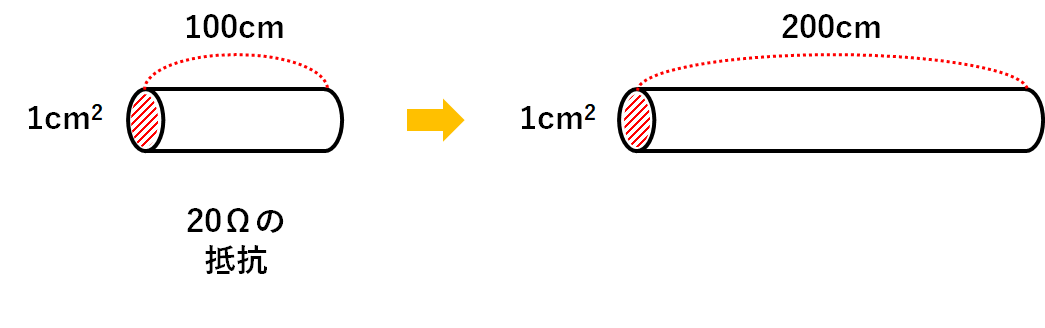
断面積1cm2・長さ100cmで20Ωの抵抗
をもっています。(↓の図)
では同じ材質Xを用いて
断面積1cm2・長さ200cmの電熱線
をつくりました。
この電熱線の抵抗はどうなるか・・・
→【電流と電圧】←や→【オームの法則】←で説明していますが
電流にとって電熱線というのは障害物です。
(抵抗・・・電流の通りにくさを表す数値)
ということは
電熱線が長くなる
↓
電流はより長い距離の障害物を通らなければならない
↓
電流は流れにくい=抵抗は大きくなる
と考えられます。
具体的には
抵抗の大きさは電熱線の長さに比例
します。
つまり
電熱線の長さが2倍・3倍・4倍・・・になると、
その抵抗も2倍・3倍・4倍・・・になる
ということです。
よって電熱線の抵抗の大きさは
$$20Ω×2=40Ω$$
となります。
POINT!!
抵抗の大きさは電熱線の長さに比例する!
2.電熱線の長さと断面積の関係
先ほどと同じ、ある材質Xでできた電熱線があります。
この電熱線は
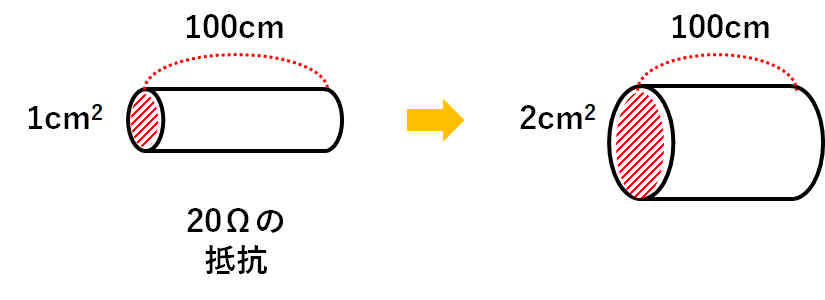
断面積1cm2・長さ100cmで20Ωの抵抗
をもっています。(さっきとまったく同じ条件)
では次にこの材質Xを使って
断面積2cm2・長さが100cmの電熱線
をつくりました。
この電熱線の抵抗はいくらになるでしょうか。
電熱線の断面積が大きくなりました。
つまり電熱線が太くなったわけです。
電熱線が太くなった
↓
電流が一度にたくさん流れることができる
↓
電流が流れやすい=抵抗は小さくなる
と考えられます。
具体的には
抵抗の大きさは電熱線の断面積に反比例
します。
つまり
電熱線の断面積が2倍・3倍・4倍・・・になると、
その抵抗は1/2倍・1/3倍・1/4倍・・・になる
ということです。
よってこの電熱線の抵抗の大きさは
$$20Ω×\frac{1}{2}=10Ω$$
となります。
POINT!!
抵抗の大きさは断面積に反比例する!
3.断面積と長さ
■電熱線の長さと抵抗の関係
長さが2倍・3倍・4倍・・・になると抵抗も2倍・3倍・4倍・・・となる。
抵抗は長さに比例する。
■電熱線の断面積と抵抗の関係
断面積が2倍・3倍・4倍・・・になると、その抵抗は1/2倍・1/3倍・1/4倍・・・になる。
抵抗は断面積に反比例する。
例題1
先ほどの材質Xを使って
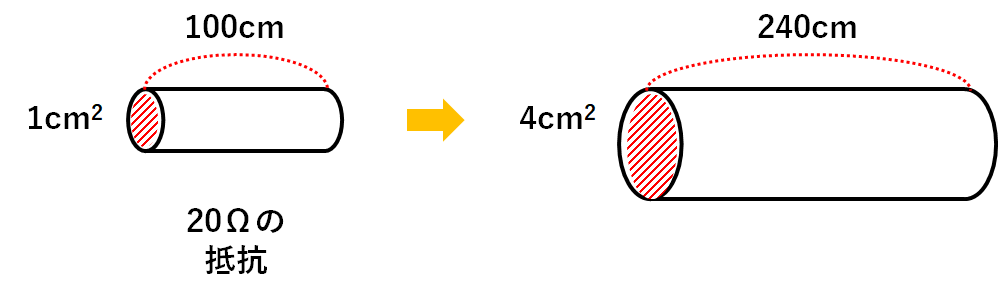
断面積4cm2・長さ240cmの電熱線P
をつくった。
(答)
もとの条件として、この電熱線は
断面積1cm2・長さ100cmで20Ωの抵抗
をもっていました。
電熱線Pは、もとの条件から
長さが2.4倍(=240÷100)
断面積が4倍(=4÷1)
です。
ということは
$$長さによって抵抗は2.4倍$$
$$断面積によって抵抗は\frac{1}{4}倍$$
になることがわかります。
よって求める抵抗の値は
$$20Ω×2.4×\frac{1}{4}=12Ω$$
とわかります。
例題2
先ほどの材質Xを使って
断面積0.8cm2・長さ40cmの電熱線Q
をつくった。
この電熱線Qの抵抗はいくらか。
(答)
もとの条件として、この電熱線は
断面積1cm2・長さ100cmで20Ωの抵抗
をもっていました。
電熱線Qは、もとの条件から
長さが0.4倍(=40÷100)
断面積が0.8倍(=0.8÷1)
です。
0.8を分数に直しておきましょう。
$$0.8=\frac{8}{10}=\frac{4}{5}$$
ということは
$$長さによって抵抗は0.4倍に$$
$$断面積によって抵抗は\frac{5}{4}倍に$$
なることがわかります。
よって求める抵抗の値は
$$20Ω×0.4×\frac{5}{4}=10Ω$$
とわかります。
4.*断面積・ちょっと応用
*ここからはやや発展的な内容を含みます。
先ほどから登場している材質X。
この材質Xをつかって円柱形をした電熱線をつくったとします。
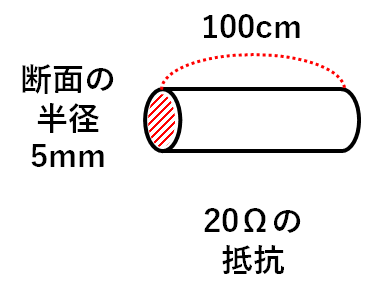
↓の図のように、断面の半径が5mm・長さ100cmの電熱線です。
この電熱線の抵抗が20Ωであったとします。
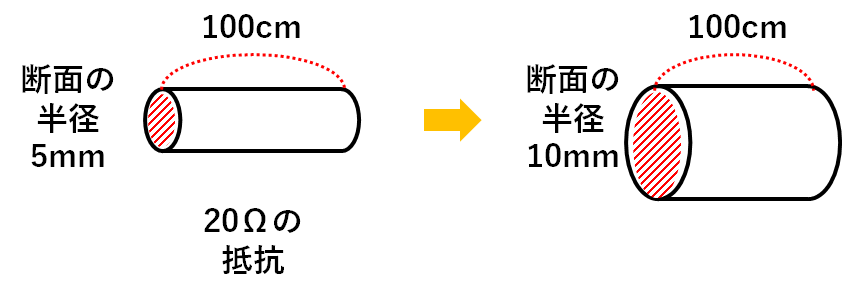
では同じ材質Xをつかって
断面の半径が10mm・長さが100cmの円柱形の電熱線R
をつくったとしましょう。
電熱線Rの断面の半径はもとの2倍です。
ということは、断面積は22=4倍です。
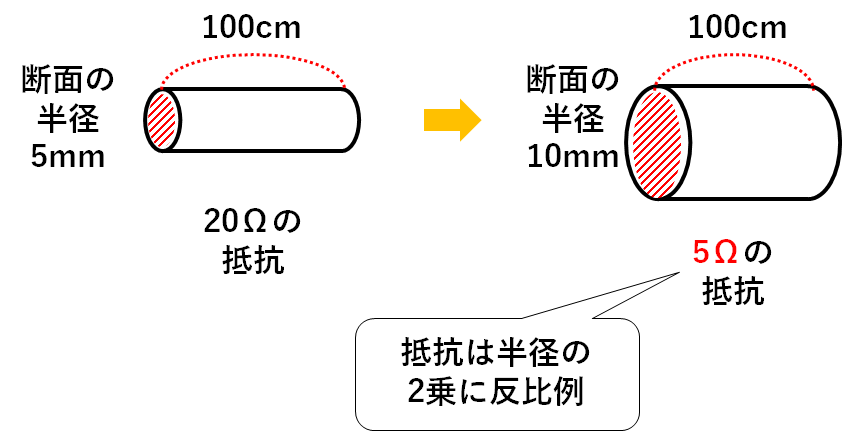
そのため抵抗は1/4倍になっているはずです。
(抵抗は、断面の半径の2乗に反比例する)
よって求める抵抗は
$$20Ω×\frac{1}{2^2}=20Ω×\frac{1}{4}=5Ω$$
となります。
断面積と断面の半径では考え方が少し異なるので要注意。
問題文をよく読むようにしましょう。



コメント(承認された場合のみ表示されます)