このページでは「重さ(質量)のある滑車を使った計算問題」について解説しています。
問題文に「滑車の質量(重さ)は考えないものとする」という条件がなければ、滑車の重さに注意しながら問題を解かなければなりません。
引っかかりやすい問題ですので、よく読んで通常の滑車の問題との違いを理解しておきましょう。
滑車を使った仕事の基本的な問題は→【滑車を使った仕事】←を参考にしてください。
そもそも「仕事とは?」を知りたい人は→【仕事とは】←を参考にしてください。
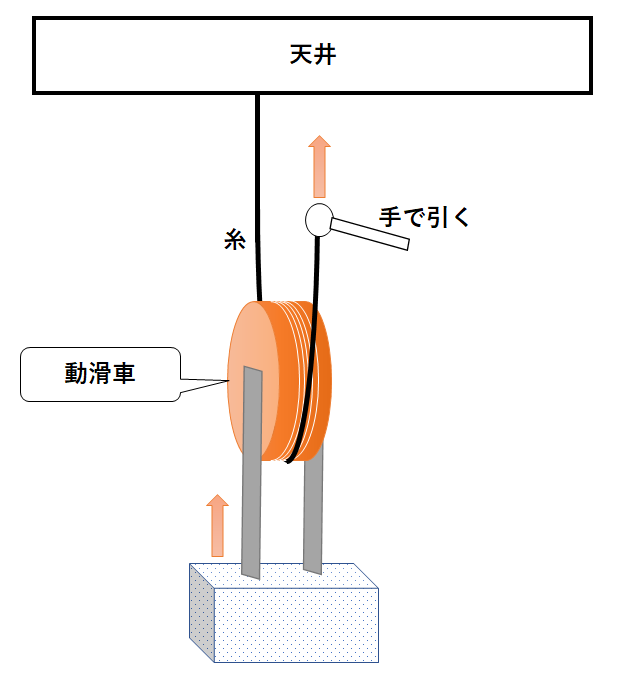
1.動滑車
■動滑車
壁や天井などに固定されていない滑車。
動滑車とは↓の図にある滑車です。
手で糸を引いたとき、滑車ごとつるしている物体が持ち上がるような場合の滑車です。
この図の滑車を正面から見たものが↓です。
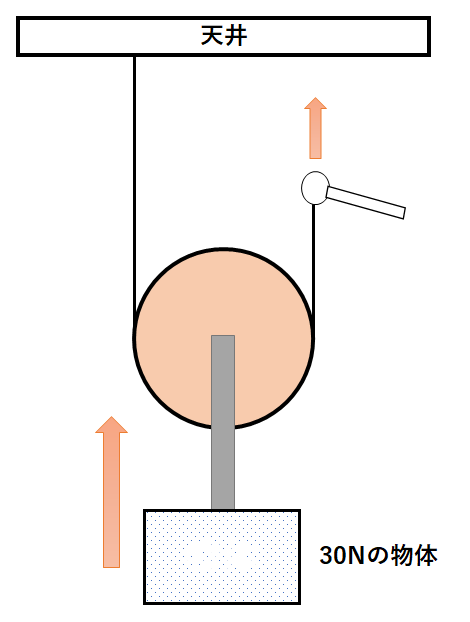
30Nの物体をつるしているとします。
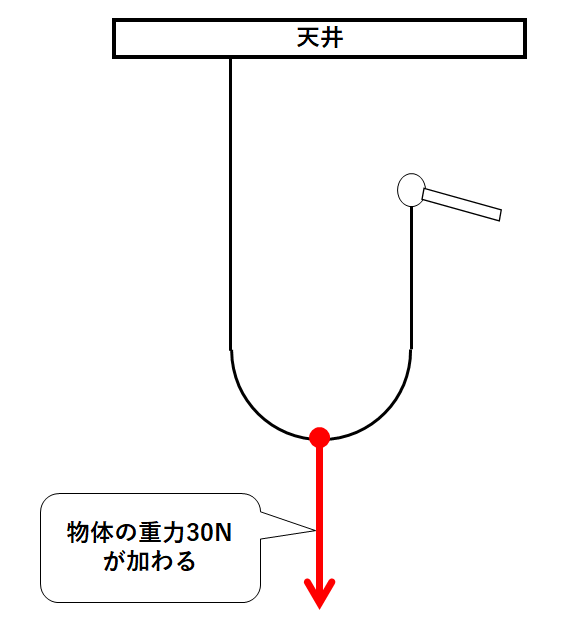
滑車を省略してみると↓のように糸が見えます。
この糸にはつるしている物体の重力30Nがそのまま加わっています。
これを天井と手の二か所で支えています。
よって天井に15N、手に15Nの力が加わります。(↓の図)
このように動滑車では
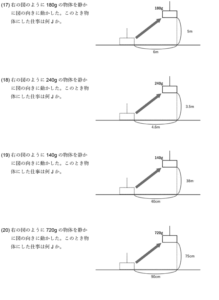
手で引く力は物体の重力の1/2倍
となります。
その代わり、
手で糸を引く距離は物体を持ち上げる距離の2倍
となります。
ここまでのお話は、滑車の重さや質量は無視して考えました。
しかし現実の滑車には質量や重さがあります。
滑車の重さや質量を考慮すると何が変わるか見ていきましょう。
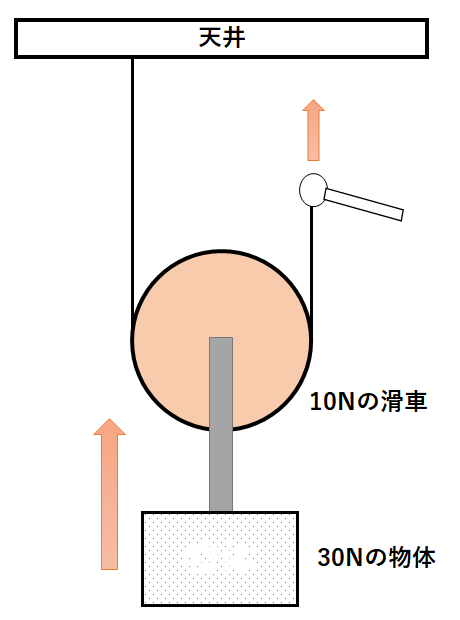
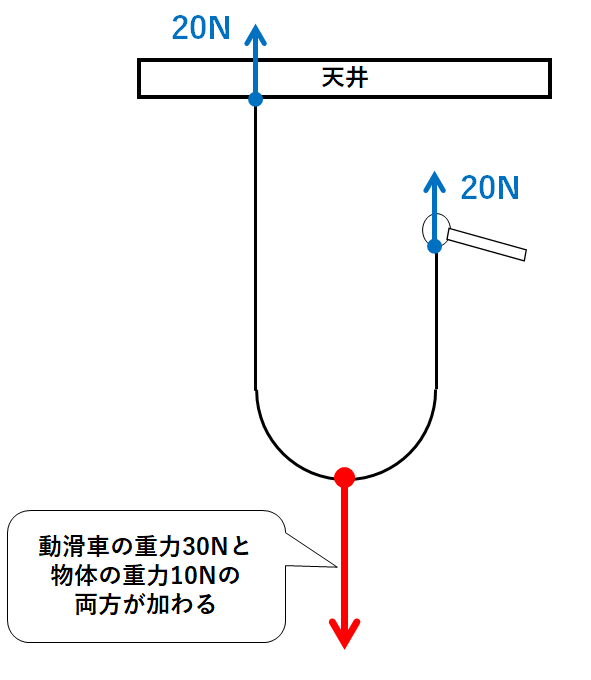
↓の装置で滑車が10Nの重さであったとします。(物体の重さは30Nで先ほどと同じです)
滑車を省略します。
糸には物体の重さ30Nに加えて、滑車の重さ10Nも加わります。(合計で40N)
この40Nを天井と手の二か所で支えています。
よって天井に20N、手に20Nの力が加わります。
このように動滑車に重さや質量がある場合は、その分、手で引く力は大きくなります。
手で糸を引く距離は、動滑車の重さの有無に関係なく、変わりません。
持ち上げたい距離の2倍を手で引く必要があります。
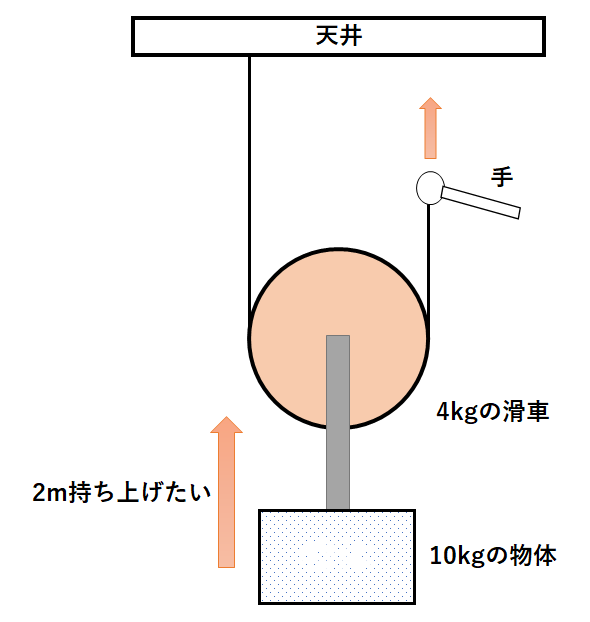
例題1
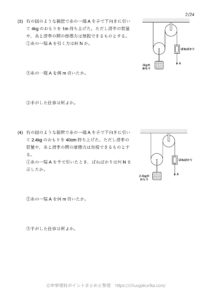
4kgの滑車と糸を使って、下の図のように10kgの物体を2m持ち上げたい。
100gの物体にはたらく重力を1Nとする。
(1)手で糸を引く力は何Nか。
(2)手で糸を引く長さは何mか。
(3)手がした仕事は何Jか。
(4)10kgの物体がされた仕事は何Jか。
(答)
(1)
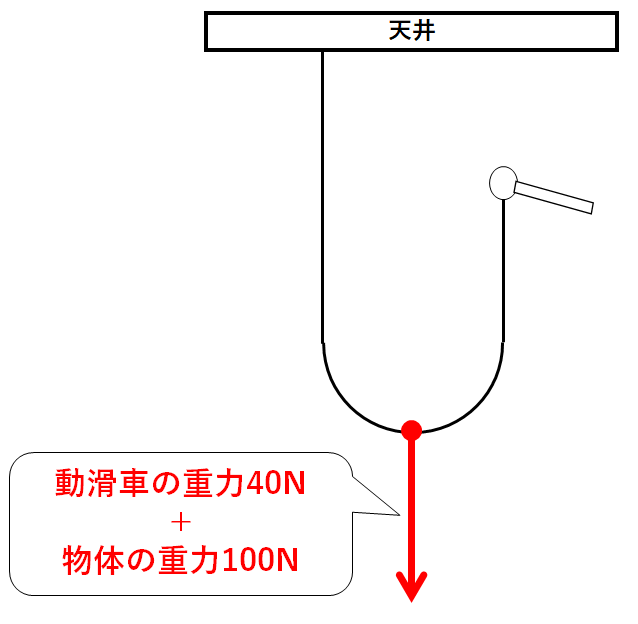
滑車を省略して、糸にはたらく力を見てみます。(↓の図)
糸には合計140Nの力がはたらきます。
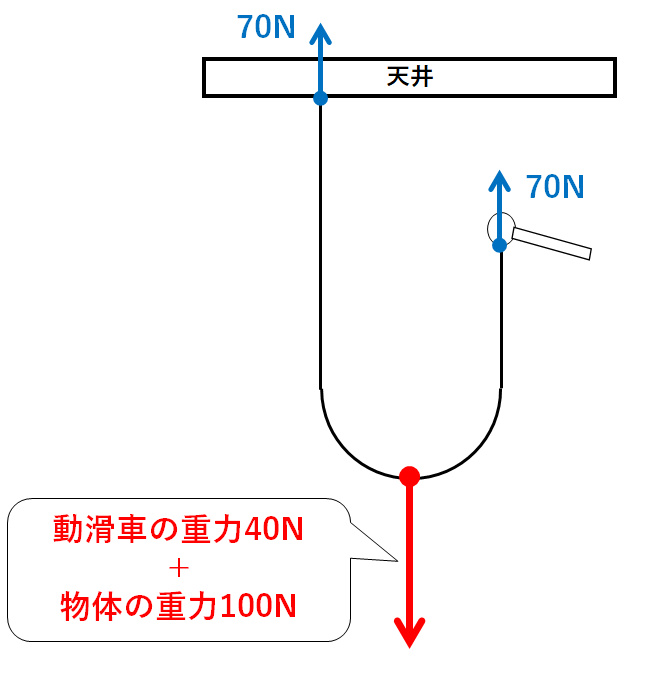
これを天井と手の2か所で支えるので(↓の図)
手で糸を引く力は70Nとなります。
(2)
物体を2m持ち上げるならば、糸をその2倍引かなければなりません。
これは滑車に重さがあろうとなかろうと関係ありません。
よって手で糸を引く長さは4mです。
(3)
仕事は次のように求められます。
仕事(J)=力(N)×力の向きに動いた距離(m)
先ほどの(1)(2)より
手で引く力=70N
手で引く距離=4m
とわかっているので
仕事=70N×4m=280J
よって手で280Jの仕事をしたことになります。
(4)
仕事には「物体のエネルギーをどれだけ変化させたか」という意味があります。
この例題1では100Nの物体を2m持ち上げています。
持ち上げているということは位置エネルギーが増加します。
※位置エネルギー(J)=重さ(N)×高さ(m)で求められます。
この問いで物体の位置エネルギーは
重さ×高さ=100N×2m=200J
増加しています。
そのため物体は200Jの仕事をされたということになります。
※大事なこと・・・
(3)と(4)の答えを見比べましょう。
手がした仕事=280J
物体がされた仕事=200J
「手がした仕事が280J」を言い換えると「手が与えた位置エネルギーが280J」です。
しかし物体が得た位置エネルギーは200J。
「手が与えた位置エネルギー」と「物体が得た位置エネルギー」が一致せず、差が80Jあるのです。
これは、手が位置エネルギーを与えた相手が「10kgの物体」だけではないからです。
手が持ち上げたのは「10kgの物体」のほかに「4kgの動滑車」があります。
つまり手は動滑車にも位置エネルギーを与えた(=仕事をした)のです。
4kgの動滑車にはたらく重力は40N。
この動滑車を2m持ち上げたので、位置エネルギーは
重さ×高さ=40N×2m=80J
増加しています。
これが先ほどの差にあてはまります。
POINT!!
・動滑車に重さや質量がある場合、物体がされた仕事=手がした仕事とはならない。
→ 手は動滑車にも仕事をしているため。
例題2
滑車、糸、ばねばかりを使って次の図のような装置をつくった。
この装置で600gの物体を1m持ち上げた。
このときばねばかりは5Nを示していた。
(1)動滑車の質量は何gか。
(2)手がした仕事は何Jか。
(3)物体がされた仕事は何Jか。
(答)
(1)
600gの物体を、動滑車を用いて持ち上げようとしています。
動滑車に重さや質量がなければ、手で引く力は3N(物体の重さ6Nの1/2)。
しかしばねばかりは5Nを示したとあります。
これは動滑車に重さがあるからです。
動滑車に重さがあると
手で引く力=(物体の重さ+動滑車の重さ)の1/2
となるので
物体の重さ+動滑車の重さ=10N
となります。
よって動滑車の重さは
10N-物体の重さ=10N-6N=4N
したがって動滑車の質量は400gとなります。
(2)
手がした仕事は
仕事(J)=力(N)×力の向きに動いた距離(m)
で求められます。
手で糸を引いた力=5N(ばねばかりの値より)
手で糸を引いた距離=1m×2=2m
したがって
手でした仕事=5N×2m=10J
よって手がした仕事は10Jです。
(3)
物体がされた仕事は、増加した位置エネルギーに等しいです。
位置エネルギーは次の式で求められます。
→ 位置エネルギー(J)=重さ(N)×高さ(m)
物体の重さ=6N
物体の持ち上がった高さ=1m
であることから
位置エネルギー=6N×1m=6J
物体がされた仕事は6Jです。
・「動滑車の質量(重さ)を考えないものとする」という問題文がない場合は要注意。
→ 動滑車の質量(重さ)を考えなければいけないことがある。
こちらもどうぞ
仕事の計算ドリルを販売中です。(PDF形式)
1つ税込220円です。
斜面を使った仕事や滑車の仕事もあります。
よければどうぞ。







コメント(承認された場合のみ表示されます)