このページでは2019年度の兵庫県立入試の問題を解説しています。(理科のみ)
問題・模範解答はこちら↓↓↓↓
https://resemom.jp/feature/public-highschool-exam/hyogo/
大問1の解説
1(1)
音の高さは、波の振動数に表れます。
高い音・・・振動数が多い
低い音・・・振動数が少ない
1(2)
振動数は以下のように求めます。
$$振動数(Hz)=\frac{振動の回数}{時間(秒)}$$
よってこの問いの場合は
$$振動数=\frac{5回}{0.01秒}=500Hz$$
2
炭酸水素ナトリウムを加熱すると
炭酸水素ナトリウム→炭酸ナトリウム+水+二酸化炭素
という反応が起こります。
この化学変化を分解といいます。
頻出の化学変化ですので必ず覚えておきましょう。
3(1)
種子になるのは胚珠の部分です。(図2のウ)
ちなみに子房(図2のエ)は受精後、果実へと成長します。
3(2)
この問いで重要なのは“減数分裂”です。
減数分裂とは、生殖細胞をつくるための特別な細胞分裂です。
※生殖細胞とは「精子や卵(動物の場合)」・「精細胞や卵細胞(植物の場合)」のこと。
これらをつくるために減数分裂をします。
このときに生殖細胞には、元と半分の本数の染色体が入ります。
POINT!!
生殖細胞に含まれる染色体数は、もとの半分!
(減数分裂による)
よってエンドウの精細胞や卵細胞には7本の染色体が含まれます。
これらが受精して受精卵ができます。
したがって受精卵の染色体数は14本にもどります。
そのためイが正解です。
大問2の解説
1(1)(2)
表1から
パパイヤのしぼり汁があれば → デンプンなし・糖あり
パパイヤのしぼり汁がなければ → デンプンあり・糖なし
よってパパイヤのしぼり汁は、デンプンを分解し、糖に変えるはたらきがあることになります。
これはアミラーゼと(だ液に含まれる消化酵素)同様のはたらきです。
1(3)
タンパク質にはたらく消化酵素としては
ペプシン(胃液に含まれる)・トリプシン(すい液に含まれる)
を覚えておきましょう。
2
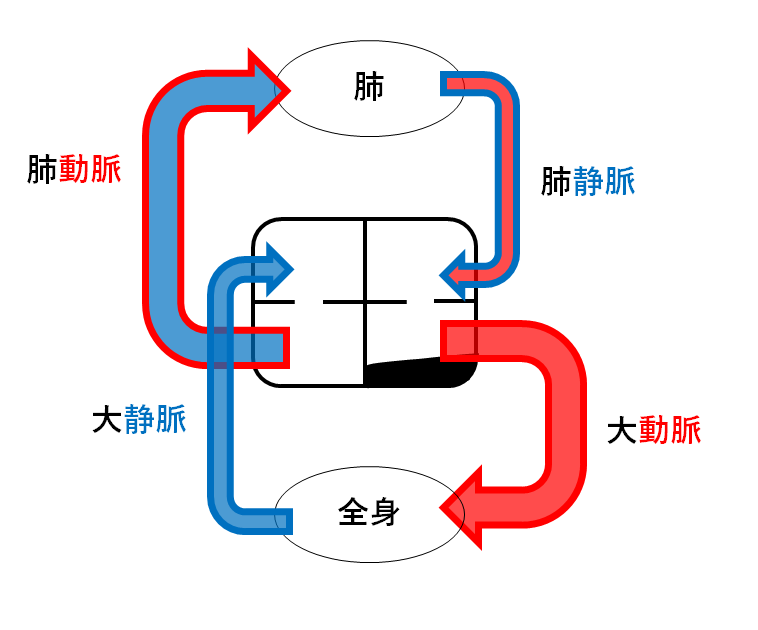
心臓の4つの部屋のうち
上の部屋・・・心房。血液が戻るための部屋。
下の部屋・・・心室。血液が出ていくための部屋。
また血管には2種類あり、
動脈・・・血液が心臓から出るための道。
静脈・・・血液が心臓にもどるための道。
そのため心房には静脈がつながっており、心室には動脈がつながっています。
大問3の解説
1(1)
硫酸の電離のようすは次のように表されます。
H2SO4 → 2H+ + SO42-
1つの硫酸分子から2個の水素イオンと1個の硫酸イオンが生じるという式です。
よってウが正解となります。
1(2)
フェノールフタレイン溶液は
酸性または中性のときは無色 ・ アルカリ性のときは赤色
になります。
また多くの酸性の水溶液は、金属を加えると水素の気体が発生します。
ア
1班では・・・
まず操作Aを行い、フェノールフタレイン溶液が赤色になっています。
つまり溶液はアルカリ性です。
この状態で操作B(マグネシウムを加える)を行っても気体は発生しません。
そのため、この選択肢は誤りです。
イ
2班では・・・
まず操作Aを行い、フェノールフタレイン溶液が無色になっています。
つまり溶液は中性か酸性のどちらかです。
この状態で操作C(硫酸を加える)を行っても、水酸化バリウムが存在しないので沈殿はできません。
そのため、この選択肢は正しいことが書かれています。
ウ
3班では・・・
まず操作Bを行い、気体が発生していません。
つまり溶液は中性かアルカリ性です。
もしアルカリ性だった場合(つまり水酸化バリウムが余っている)、この状態で操作C(硫酸を加える)を行うと、水酸化バリウムと硫酸が中和し、沈殿が生じる可能性があります。
そのため、この選択肢は誤りです。
エ
4班では・・・
まず操作Bを行い、気体が発生しています。
つまり溶液は酸性です。
この後、フェノールフタレイン溶液を加えても、無色のままとなります。
そのため、この選択肢は正解です。
2(1)
表2から、塩酸50cm3を中性にするには、水酸化ナトリウム水溶液が30cm3必要であることがわかります。
ビーカーAでは水酸化ナトリウム水溶液を加えた量が0cm3なので、液全体は酸性。
BTB溶液は黄色になります。
ビーカーFでは水酸化ナトリウム水溶液を加えた量が50cm3。
塩酸を中性にするには多すぎます。
よって水酸化ナトリウム水溶液が余るので液全体はアルカリ性。
BTB溶液は青色になります。
2(3)
問題文より、図2はうすい水酸化ナトリウム水溶液50cm3に含まれるイオンを表しています。
うすい水酸化ナトリウム水溶液50cm3には
・ナトリウムイオンが5個
・水酸化物イオンが5個
含まれています。
ここでビーカーDに注目。
ビーカーDでは、塩酸50cm3と水酸化ナトリウム水溶液30cm3が中和して、中性になっています。
つまり
塩酸50cm3に含まれる水素イオンの数=水酸化ナトリウム水溶液30cm3に含まれる水酸化物イオンの数
となっているはずです。
うすい水酸化ナトリウム水溶液30cm3には
・ナトリウムイオンが3個
・水酸化物イオンが3個
含まれているはず。
よって塩酸50cm3には
・水素イオンが3個
・塩化物イオンが3個
含まれていることとなります。
したがってウが正しい様子を表していると言えます。
2(5)
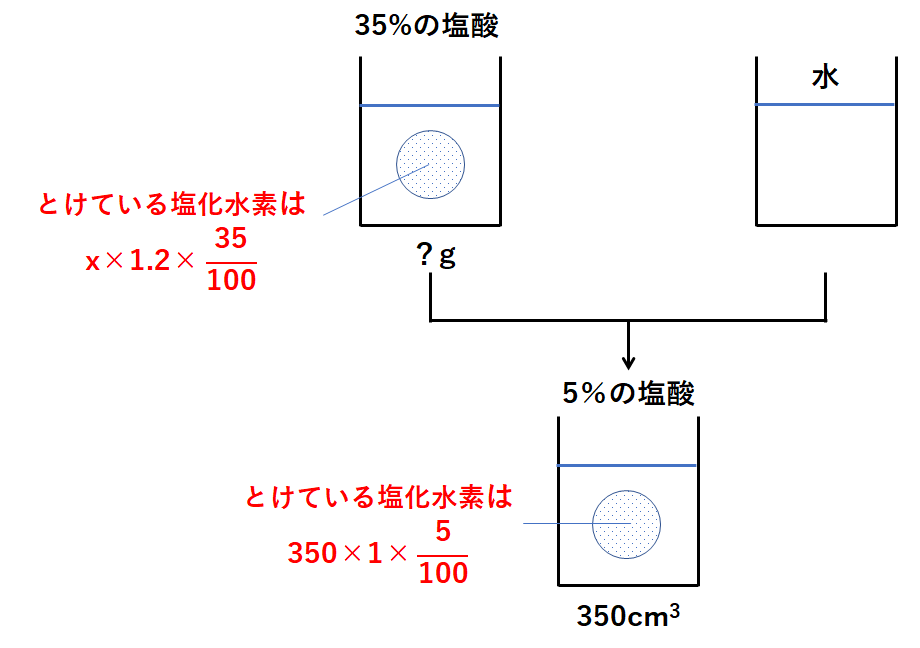
使用した35%の塩酸の体積を x(cm3)とします。
その密度が1.2g/cm3であるので
$$35%塩酸の質量(g)=体積(cm^3)×密度=x×1.2=1.2x(g)$$
と表されます。
この35%塩酸中の溶質の量は
$$溶質=水溶液全体×\frac{濃度}{100}=1.2x×\frac{35}{100}・・・①$$
となります。
一方で、作りたい塩酸は、5%塩酸350cm3です。
この5%塩酸350cm3の質量は
$$5%の塩酸の質量(g)=体積(cm^3)×密度=350×1=350g$$
この5%塩酸に溶けている溶質の量は
$$溶質=水溶液全体×\frac{濃度}{100}=350×\frac{5}{100}・・・②$$
35%塩酸を水でうすめて5%塩酸にしているだけなので、溶質の量は変わりません。
すなわち①と②は等しいはずです。(↓の図)
よって次のような式になります。
$$1.2x×\frac{35}{100}=350×\frac{5}{100}$$
これを解いて
$$x=41.66・・・$$
四捨五入して42cm3となります。
POINT!!
水溶液を水でうすめる問題
→ 水でうすめても溶質の量は変わらないことを利用しよう。
大問4の解説
1(3)
表1の天気記号から15日の神戸の天気のみくもりです。
ア~ウで神戸がくもりとなるのはウです。
(神戸のそばに寒冷前線があるため)
よって15日の天気図はウです。
アとイの選択は難しいです。
目安となるのは左下の高気圧でしょう。
高気圧や低気圧などは偏西風によって西から東へ移動するため、イ→アの順序であることがわかります。
そのため13日がイ、14日がアとなります。
2(1)①
実際に含まれている水蒸気の量を求めるには次の式を使います。
$$実際の水蒸気量=飽和水蒸気量×\frac{湿度}{100}$$
室温が17.6℃であるので飽和水蒸気量は15gです。
よって
$$実際の水蒸気量=15×\frac{20}{100}=3g$$
したがってイが正解です。
2(1)②
外気温5.4℃で水滴が生じたので、空気の露点が5.4℃になっているといえます。
そのため含まれている水蒸気量は空気1m3あたりで7gとわかります。
POINT!!
露点では、実際に含まれている水蒸気量と飽和水蒸気量が一致している。
(実際の水蒸気量=飽和水蒸気量)
前問より、もともと3gの水蒸気をふくんでいたので
$$7-3=4g$$
の水蒸気が増えた(空気1m3あたり)とわかります。
部屋の空気は30m3あるので、部屋全体で増えた水蒸気の量は
$$4g×30=120g$$
となります。
2(2)
1日目の気温は15.2℃です。
そのため図2より飽和水蒸気量は13gです。
湿度は65%なので、1日目の空気に含まれる水蒸気量は
$$実際の水蒸気量=13×\frac{65}{100}=8.45g$$
8.45gの水蒸気を含んでいる空気。
この空気の露点は、図2より約8℃です。
15.2℃から約8℃まで気温が下がれば、水滴ができ始めるということです。
(この水滴が雲となる)
よって
$$15.2-8=7.2℃$$
の気温が下がります。
そのためには、空気は720m上昇しなければなりません。
(問題文より、空気は100m上昇につき1℃下がる)
選択肢ア~エのうち、最も近いのはイとなります。
同様にして、2日目、3日目の実際の水蒸気量を求めると
$$2日目の実際の水蒸気量=11×\frac{45}{100}=4.95g$$
$$3日目の実際の水蒸気量=10×\frac{70}{100}=7g$$
よって2日目、3日目の空気の露点は
・2日目の空気の露点は約0℃
・3日目の空気の露点は約5.4℃
2日目の気温は12.4℃であるので
$$12.4-0=12.4℃$$
の気温が下がれば雲が生じます。
その高さは1240mです。(問題文より、空気は100m上昇につき1℃下がる)
3日目の気温は11.0℃なので
$$11.0-5.4=5.6℃$$
の気温が下がれば雲が生じます。
その高さは560mです。(問題文より、空気は100m上昇につき1℃下がる)
よって雲のできる高さは2日目が最も高く、3日目が最も低いと考えられます。
2(3)
空気が上昇すると、周囲の気圧が下がります。
そのため、上昇した空気は膨張(体積が増加)します。
体積が増加するので、1m3あたりの水蒸気量は減少します。
そのため露点は下がってしまいます。
陸地での気温と露点との差が大きいということなので、雲のできる高さはより高くなります。
大問5の解説
1(1)
圧力は以下のように求められます。
$$圧力(N/m^2)=\frac{力(N)}{面積(m^2)}$$
この式の形を変えると
$$力(N)=圧力(N/m^2)×面積(m^2)・・・①$$
とできます。
この問いでは圧力が810Pa(=810N/m2)、面積が3cm×3cm=9cm2です。
また
$$9cm^2=\frac{9}{10000}m^2$$
であるので、①式を利用すると
$$力(N)=810Pa×\frac{9}{10000}m^2=0.729N$$
立方体の底面には0.729Nの力がはたらいていることになります。
この力は立方体の重さに等しいので、質量に変換すると
$$0.729N → 72.9g$$
となります。
立方体の一辺は3cmなので、その体積は27cm3。
したがって立方体の密度は
$$密度(g/cm^3)=\frac{72.9g}{27cm^3}=2.7g/cm^3$$
となります。
1(2)
地道に計算してみましょう。
直方体の体積は
$$6cm×6cm×3cm=108cm^3$$
直方体と立方体の密度はともに等しく2.7g/cm3です。
よって直方体の質量は
$$直方体の質量(g)=体積×密度=108cm^3×2.7g/cm^3=291.6g$$
したがって直方体が床に加える力は
$$291.6g → 2.916N$$
また直方体と床が接している面積は
$$6cm×6cm=36cm^2=\frac{36}{10000}m^2$$
以上から直方体が床に加える圧力は
$$圧力=\frac{力}{面積}=2.916÷\frac{36}{10000}=810N/m^2$$
$$810N/m^2=810Pa$$
であるので、直方体が床に加える圧力は810Paとなります。
計算せずに考えてみましょう。
図1の立方体と直方体は高さがともに3cmです。
よって立方体と直方体の体積比は、底面積の比で決まります。
底面積の比は
$$立方体:直方体=3cm×3cm:6cm×6cm=9:36=1:4$$
です。
立方体と直方体の体積比も1:4です。
互いに密度は等しいので立方体と直方体の質量比も1:4。
ということは重さの比も1:4です。
したがって直方体を床に置いたとき
・直方体から床にはたらく力は、立方体を置いたときの4倍
・直方体が床と接する面積は、立方体を置いたときの4倍
となっているので
直方体を置いたときの圧力は立方体を置いたときと等しくなります。
よって810Paが正解となります。
1(3)
円柱Aと円柱Bは半径が4cm、8cmです。
つまり半径の比は1:2です。
そのため底面積の比は
$$A:B=1^2:2^2=1:4$$
です。
A、Bともに高さが3cmです。
体積の比は底面積の比に等しく
$$A:B=1:4$$
です。
同じ密度の物質でできているので、AとBの質量比も
$$A:B=1:4$$
よって
床に加わる力は A:B=1:4
床に接する面積は A:B=1:4
そのため
Aが床に加える圧力=Bが床に加える圧力
となります。
同じように考えると、円柱A~Cから床にはたらく圧力は互いに等しくなります。
円柱A~Cを置いただけでは、床にはたらく圧力は等しいですが、
・円柱Aには立方体を4個
・円柱Bには立方体を12個
・円柱Cには立方体を40個
以上の立方体をのせていくため、どれも圧力が増加します。
それぞれ
$$\frac{のせた立方体の重さ}{円柱が床と接する面積}$$
の分だけ圧力が増加します。
本来は「立方体の重さ」で計算すべきですが
$$\frac{のせた立方体の個数}{円柱が床と接する面積}$$
の計算を円柱A~Cの場合で行い、大小関係を比較する方が楽です。
円柱Aの場合は
$$\frac{のせた立方体の個数}{円柱が床と接する面積}=\frac{4個}{16cm^2}$$
円柱Bの場合は
$$\frac{のせた立方体の個数}{円柱が床と接する面積}=\frac{12個}{64cm^2}$$
円柱Cの場合は
$$\frac{のせた立方体の個数}{円柱が床と接する面積}=\frac{40個}{144cm^2}$$
$$\frac{12}{64}<\frac{4}{16}<\frac{40}{144}$$
であるので
圧力が最も大きいのは円柱Cの場合、圧力が最も小さいのは円柱Bの場合となります。
3(1)
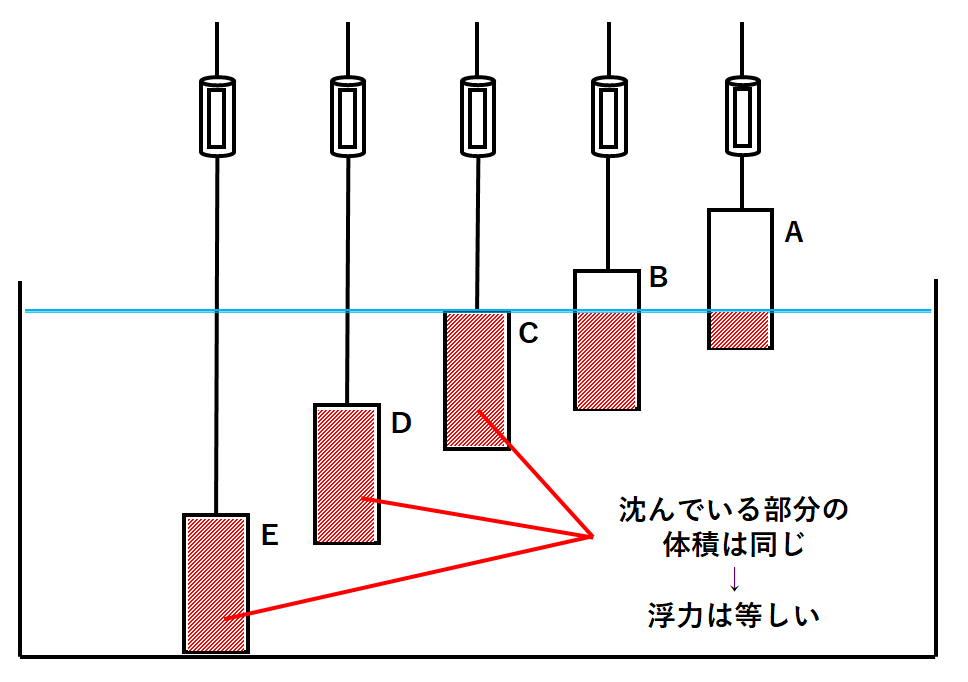
この実験でばねばかりが示す値は
おもりの重力とおもりにはたらく浮力の差
です。
また浮力の大きさは
沈んでいる部分の体積
で決まります。
POINT!!
浮力の大きさは、水中に沈んでいる部分の体積で決まる。
→ 沈んでいる部分の体積に変化が無ければ、浮力は一定。
おもり全体が水中に沈んでいる間は、浮力は一定です。
しかしおもりが水面から出始めると浮力は小さくなっていきます。
よってばねばかりは
・おもり全体が水中に沈んでいる間は一定
・おもりが水面から出始めると大きくなる
ということになります。
それを表すグラフはアのみです。
3(2)
ばねばかりの値が1.8N、おもりの重さが3Nであることから
$$おもりにはたらく浮力=3N-1.8N=1.2N$$
浮力とは、水からおもりにはたらく上向きの力です。
この場合、おもりの底面を1.2Nで押していることになります。
水圧を求めなければなりませんが、水圧も圧力の一種。
圧力の求め方と同じです。
よって
$$水圧=\frac{力}{面積}=1.2N÷\frac{8}{10000}m^2=1500N/m^2$$
$$1500N/m^2=1500Pa$$
そのため水圧は1500Paとなります。
【別解】
アルキメデスの原理を使ったやや発展的な解法です。
水圧は水面からの深さで決まります。
水の場合、その水圧は水深1cmで100Paです。
よって底面の水面からの深さがわかれば、水圧を求めることができます。
まず浮力を考えましょう。
浮力は押しのけた液体の重さで決まります。
POINT!!
アルキメデスの原理
→ 浮力の大きさは、押しのけた液体の重さに等しい。
ばねばかりの値が1.8N、おもりの重さが3Nであることから
$$おもりにはたらく浮力=3N-1.8N=1.2N$$
浮力が1.2Nということは、120gの水を押しのけたということです。
水の密度は1g/cm3なので
$$水の体積=\frac{質量}{密度}=120cm^3$$
したがっておもりの水中に沈んでいる部分の体積は120cm3です。
おもりの底面積は8cm2なので
$$おもりの沈んでいる部分の高さ=120cm^3÷8cm^2=15cm$$
水圧の大きさは、深さ1cmで100Paあります。
15cmの深さならば、水圧は1500Paです。
よって1500Paと求めることができます。

コメント(承認された場合のみ表示されます)
大問3 2(5)
濃度と密度の関係がおかしくないですか?
水と5%塩酸の密度が同じものとして扱われています。
確かに少数第一位で四捨五入すれば密度1g/cm3なのでしょうが
体積と質量で連立方程式をたてると計算不能になります
NASSOONABIT様
コメントありがとうございます。
差し支えなければどのような連立方程式を立てられたか教えていただいてよろしいでしょうか?