中3物理【*瞬間の速さ】

1．瞬間の速さ

■瞬間の速さ

一瞬一瞬で持つ速さのこと。

※平均の速さについては→【速さの測定・記録タイマー】←参考に。

ここでは瞬間の速さの求め方を説明します。

瞬間の速さを求めるための公式はありません。

平均の速さの公式で代用するしかありません。

$$平均の速さ＝\frac{距離}{時間}$$

瞬間の速さを求めるには

瞬間の速さは、その瞬間を時間的中点とする区間の平均の速さに等しい

ということを利用します。

これはどういう意味かというと・・・

例えば「1.0秒後の瞬間の速さを求めよ」と言われれば・・・

「1.0秒」を時間的中点とする区間として

「0秒後～2.0秒後」という区間や「0.5秒後～1.5秒後」という区間

を取ってきます。

「1.0秒」を真ん中とする時間の区間を取るわけです。

例として、テストの平均点を考えてみましょう。

Aくんの今回の数学のテストの平均点は58点でした。

これは「ちょうど真ん中にあたる生徒の点数」に等しいですよね？

平均とは「真ん中の生徒の点数」に等しいのです。

それと同じで

「2秒後～4秒後の平均の速さ」＝「3秒後（2秒後と4秒後の真ん中）の瞬間の速さ」

ということになるんです。

【例題】

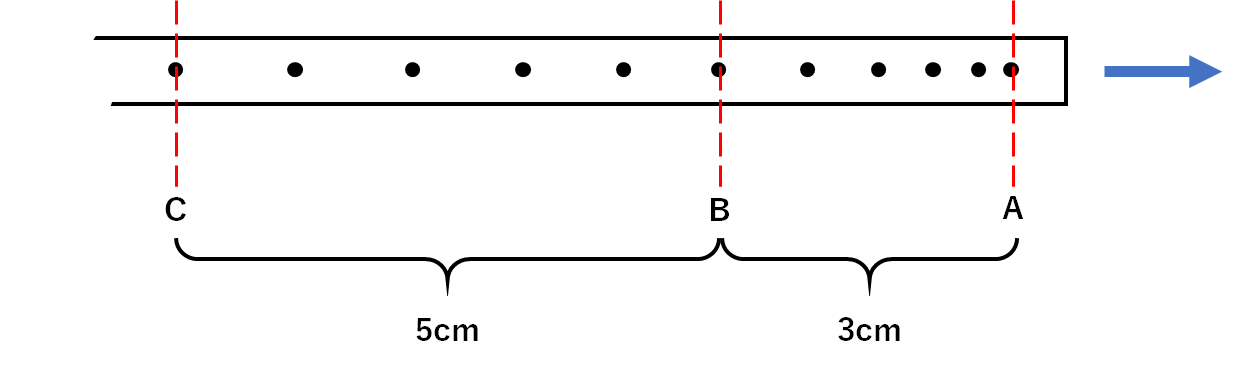
台車が矢印の方向に動いたときの記録テープの様子が上図である。

点Aを記録したのがを0秒後として次の問いに答えよ。

ただし記録タイマーは1秒間に50打点したものとする。

(1)　0秒後から0.2秒後までの平均の速さを求めよ。

(2)　0.1秒後の瞬間の速さを求めよ。

(3)　0.15秒後の瞬間の速さを求めよ。

(答)

(1)

Aが0秒後の点ですから、Bは0.1秒後、Cは0.2秒後の点となります。

$$0秒後～0.2秒後の平均の速さ＝\frac{3cm＋5cm}{0.2s}＝40cm/s$$

となります。

よって40cm/sが正解です。

(2)

0.1秒後の瞬間の速さ＝0秒後～0.2秒後の平均の速さです。

つまり(1)より

0秒後～0.2秒後の平均の速さ＝40cm/s

ですので

0.1秒後の瞬間の速さ＝40cm/s

となります。

よって40cm/sが正解です。

(3)

0.15秒後の瞬間の速さ＝0.1秒後～0.2秒後の平均の速さです。

$$0.1秒後～0.2秒後の平均の速さ＝\frac{5cm}{0.1s}＝50cm/s$$

ですので

0.15秒後の瞬間の速さ＝50cm/s
となります。

よって50cm/sが正解です。

しかしながら・・・

高校入試の問題では「瞬間の速さを求めよ」という表記はほとんどありません。

多くの場合「●●秒後の速さを求めよ」と書いてあります。

つまり「瞬間」という言葉が表記されていません。

「3秒後の速さを求めよ」とあれば「3秒後の瞬間の速さを求めよ」ということ。

そのため「2秒～4秒の平均の速さを求める」ことになるわけです。

※この瞬間の速さの求め方は・・・

「速さが時間に比例して変化する」運動にしか用いることはできません。

自由落下や摩擦のない斜面を物体がすべりおりる運動などです。

ただし高校入試では「速さが時間に比例して変化する運動」しか出題されないのであまり気にしなくてもよいです。