中3物理【*斜面上の物体の運動】

*このページは中学校内容を飛び越えた内容が含まれています。

1．斜面上の物体の運動

中学理科で学習する運動は主に以下の2つです。

 

 

 

①物体に力が加わると、その物体の運動の様子は変化する。

→自由落下のように重力が作用し続けると、速さは一定の割合で増加する。

 

 

 

②物体に力が加わらないと、その物体の運動の様子は変化しない。

→静止し続けている物体は静止し続ける。等速直線運動をしている物体は、等速直線運動をし続ける。

※→【いろいろな運動】←を参考に。

 

 

 

ここでは①について詳しく見ます。

 

 

 

物体に力が加わるとその物体の運動の様子は変化します。

 

 

 

さらに物体に一定の大きさの力が加わり続ける（同じ大きさの力がはたらき続ける）と、その物体の速さは一定の割合で変化します。

このような運動を*等加速度直線運動といいます。（*高校内容なので名称は暗記不要）

 

 

 

自由落下も等加速度直線運動の1つです。

自由落下では、物体に重力がはたらき続けています。（重力は一定のまま）

そうすることで、物体の速さが一定の割合で増加します。

 

 

 

下図のように摩擦のないなめらかな斜面に物体をおいたとき、この物体も等加速度直線運動をします。

 

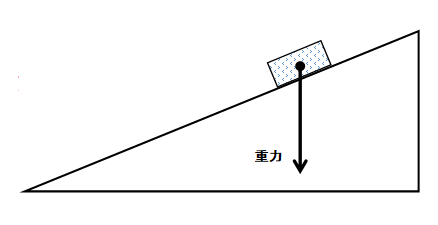
ではこの物体の重力の分力を考えてみましょう。

※作図方法は→【力の合成・分解】←を参考に。

 

 

 

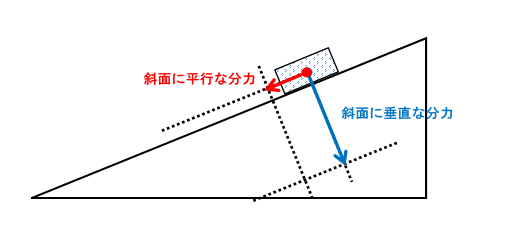
重力の分力は↓の図のようになります。

 

物体にはたらく力はこれだけではありません。

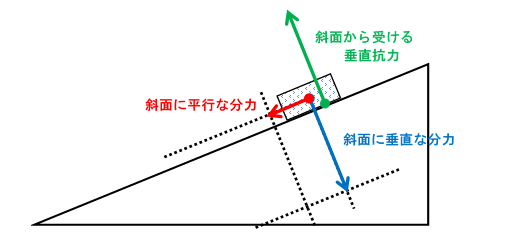
斜面から垂直抗力を受けます。（↓の図）

 

※抗力の作用点は少しずらしています。

 

 

 

この垂直抗力と重力の斜面に垂直な分力がつり合い、打ち消し合います。

よって重力の斜面に平行な分力のみが残ります。（↓の図）

 

斜面にいる間は、この力がはたらき続けるので物体の速さは変化します。

 

 

 

この力の大きさは斜面を下っている間は一定。

 

 

 

よって速さの変化も一定（一定の割合で速さが増加）。

つまり等加速度直線運動をするということです。

 

 

 

2．斜面の傾きを変えてみる

摩擦のないなめらかな斜面に物体をおいたときにはたらく重力の分力を考えます。

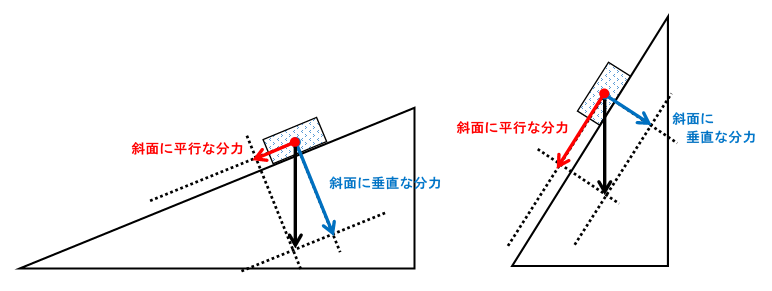
ここで物体はそのままで斜面の傾きを変えて、分力の大きさを比べましょう。(↓の図)

 

 

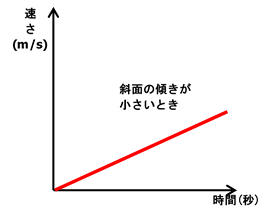
①斜面の傾きが小さいとき

重力の斜面に平行な分力が小さくなったことがわかります。

つまり速さの変化の割合は小さくなります。

よって「時間－速さのグラフ」の傾きは小さくなります。

 

 

 

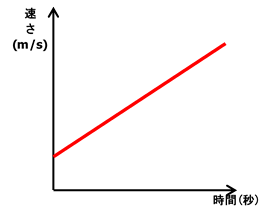
②斜面の傾きが大きいとき

重力の斜面に平行な分力が大きくなったことがわかります。

つまり速さの変化の割合は大きくなります。

よって「時間－速さのグラフ」の傾きは小さくなります。

 

 

3．*加速度

*教科書内容を超えています。

 

■加速度

1秒あたりにどれだけ速さが増加しているかを表す値。

 

 

自由落下や斜面上の物体の運動（どちらも等加速度直線運動）では、時間と速さは以下のように変化します。

（時間に比例して速さが変化。初速がなければ原点を通る）

 

 

ある等加速度直線運動で以下のような「時間－速さのグラフ」が得られたとします。

 

 

3秒後から5秒後の速さの変化を見てみましょう。

 

 

 

速さは

15m/sから20m/sへと増加

しています。

 

 

 

2秒間の間に

20m/s－15m/s＝5m/s

の速さの増加が見られます。

 

 

 

つまり1秒あたり2.5m/sの速さが増加していることになります。

 

 

 

この値が加速度です。

この値は「時間－速さのグラフ」を1次関数としてみたときの傾き（変化の割合）にあたります。

 

 

 

また加速度は「速さの変化」なので「どのような大きさの力がはたらいているか」で決まります。