*このページは発展的な内容を含みます。
1.道具を使った仕事
■仕事
→【仕事の基本】←を参考に
物体に力を加えて、力の向きに物体を動かすこと。
そして物体の持つエネルギーを変化させること。
仕事(J)=力(N)×力の向きに動いた距離(m)
仕事(J)=エネルギーの変化量
2.組み合わせ滑車
■動滑車
・手が引く力は1/2倍
・手が引く長さは2倍
となる。
→【道具を使った仕事①】←も参考に!
例題5
滑車を使って次の図のような装置を組み立てた。
この装置の糸の一端を手で引き、20Nの物体を3m持ち上げたい。
ただし滑車の質量、摩擦や空気抵抗は考えない。
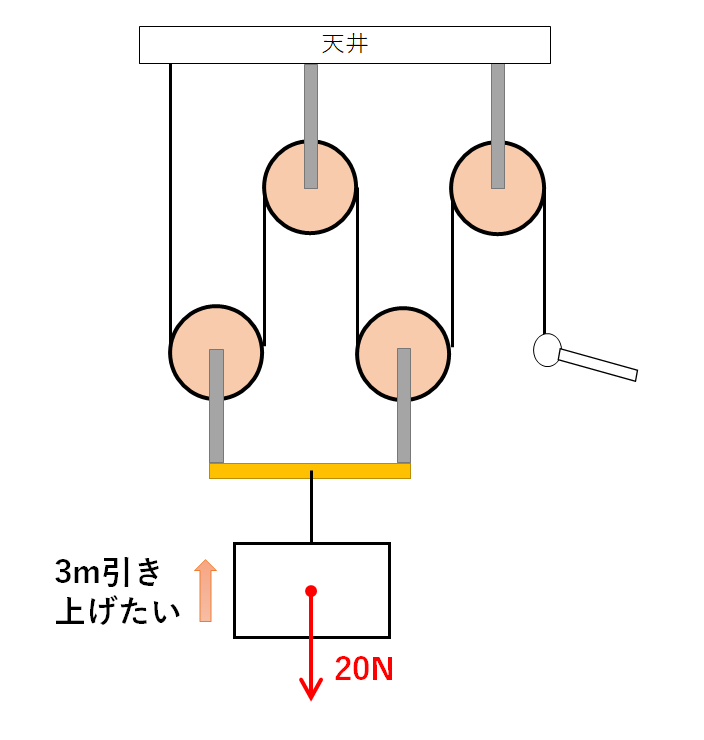
(1)糸を引く力は何Nか。
(2)糸を何m引けばよいか。
(3)手がした仕事は何Jか。
(答)
(1)
まずこの20Nの物体を黄色の棒の両端の部分2か所で支えています。
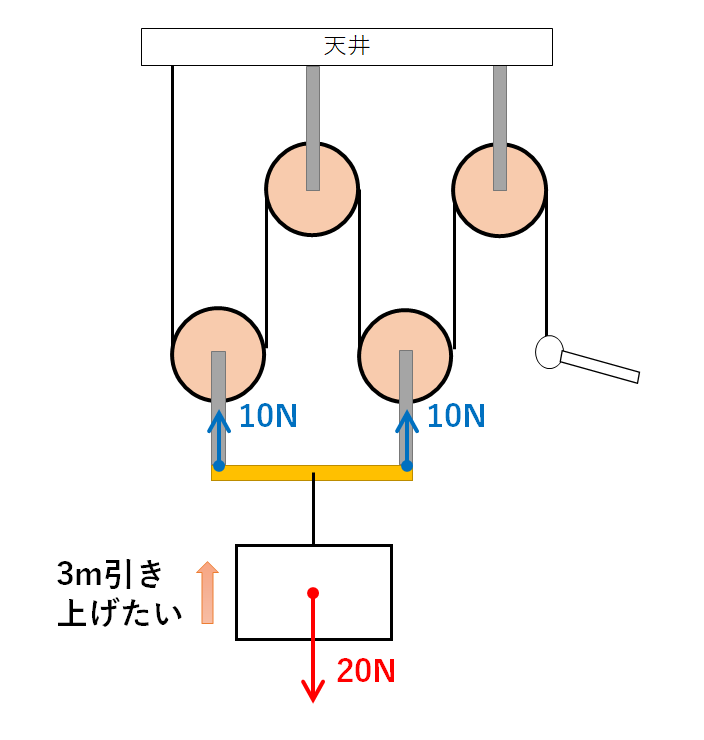
その力がさらに動滑車を支えているので
動滑車の左右の糸には5Nずつ力がはたらいています。
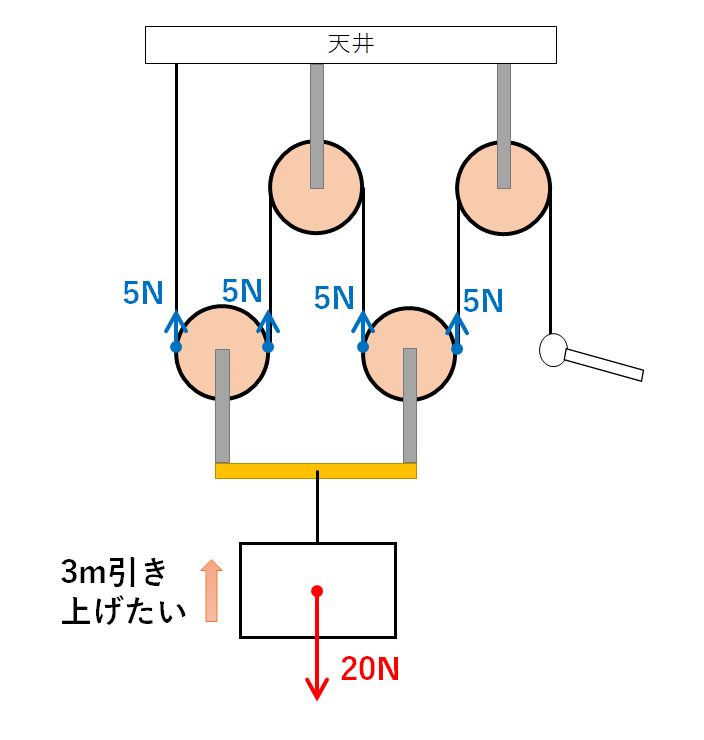
結果的に天井で5N、手で5Nという力で支えることになります。
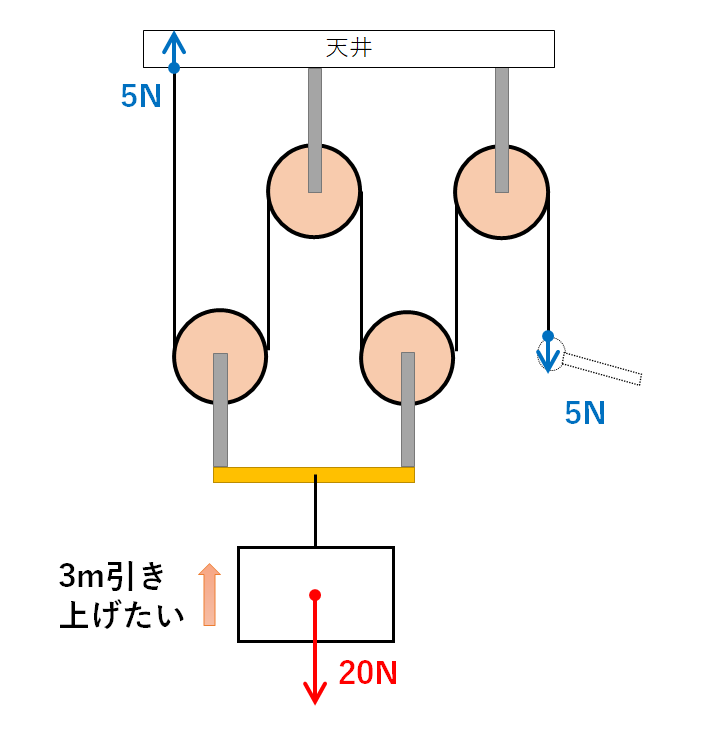
よって正解は5Nです。
(2)
道具を使っても使わなくても仕事は変わりません(仕事の原理)。
物体にしなければならない仕事は
滑車の重さを考えなくてよいので
20N×3m=60J
です。
(1)より手で引く力は5Nですから、手で引く長さは
60J÷5N=12m
となりますね。
よって正解は12mです。
※手で引く力が物体の重さの1/4倍で済んでいるわけなので、引く長さは4倍になるはずです。
(3)
滑車の重さは考えなくてよいので
(2)より60Jが正解となります。
組み合わせ滑車は動滑車の数と組み合わせ方に注意です。
まず滑車に重さがあるかないかをチェック。
次に手で糸を引く力を考える、という順で考えましょう。
2.てこを使った仕事
例題6
下図のように「てこ」を用いて2kgの物体を3m持ち上げたい。
そこでてこの右端を一定の大きさの力で1m押した。
ただし摩擦や空気抵抗は考えないものとする。
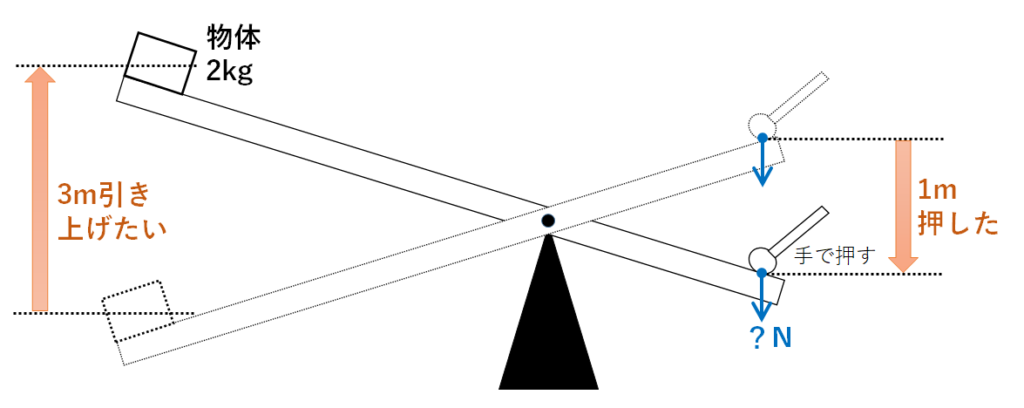
(1)てこの右端に加えた力は何Nか。
(2)手がした仕事は何Jか。
(答)
(1)
2kgの物体の高さが3m上がっています。
つまり位置エネルギーが増加しています。
仕事=エネルギーの変化量ですから
物体がされた仕事=20N×3m=60J
となります。
つまり手がした仕事も60Jとなりますね。
手で1m押しているので、加えた力は
60J÷1m=60N
となります。
よって正解は60Nです。
(2)
さきほどの(1)より60Jが正解です。
例題7
下図のように「てこ」を用いて6kgの物体を1m持ち上げたい。
そこでてこの右端を一定の大きさの力で押した。
ただし摩擦や空気抵抗は考えないものとする。
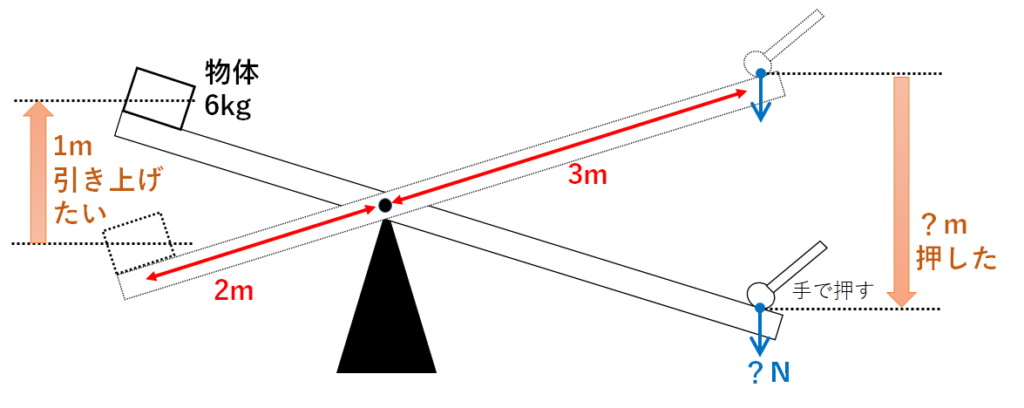
(1)てこの右端を何m押せばよいか。
(2)てこの右端に加えた力は何Nか。
(3)手がした仕事は何Jか。
(答)
(1)
さきほどと異なるのは
てこの右端を押した「力の大きさ」「距離」ともにわからないことです。
図中の赤色の部分の長さ「2m」と「3m」を利用します。
(支点からの距離=うでの長さと呼びます)
以下のような三角形を考えましょう。
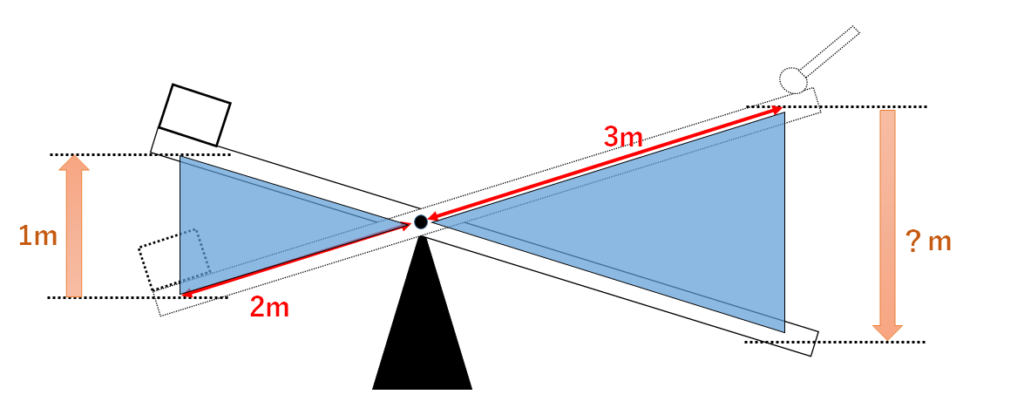
これは互いに相似な関係にありますね。
相似比は2m:3m=2:3です。
つまり・・・
左端を1m持ち上げたい、ならば右端はx(m)押すとすると
2:3=1m:x(m)
よってx=1.5mとなります。
正解は1.5mです。
(2)
6kgの物体の高さが1m上がっています。
つまり位置エネルギーが増加しています。
仕事=エネルギーの変化量ですから
物体がされた仕事=60N×1m=60J
となります。
つまり手がした仕事も60Jとなりますね。
(1)より手で1.5m押しているので、加えた力は
60J÷1.5m=40N
となります。
よって正解は40Nです。
(3)
正解は、(2)より60Jです。
■力のモーメント
例題7について下図のようなことを考えてみましょう。
てこの左端には60N、右端には40Nの力がはたらいていました。
またうでの長さは2mと3mです。
支点から左について60N×2m=120N・mとなります。
支点から右について40N×3m=120N・mとなります。
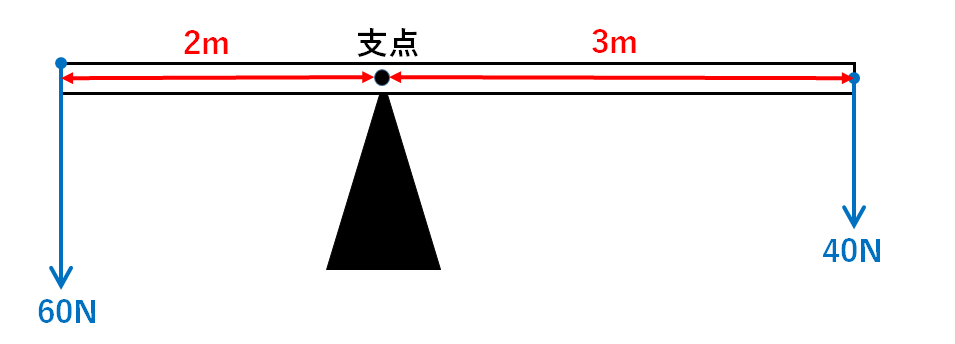
このように力×うでの長さを力のモーメントと言います。
力のモーメントとはてこを回転させる力のはたらきのことです。
左端60Nの力しか加わっていないとするとてこは反時計回りに回転しますよね。
この左端60Nはてこを反時計回りに回転させるはたらきがあります。
このはたらきの強さが60N×2m=120N・mと求められるわけです。
一方で右端40Nの力はてこを時計回りに回転させるはたらきがあります。
このはたらきの強さが40N×3m=120N・mとなるのです。
いま反時計回りのモーメントと時計回りのモーメントの大きさが等しいので
このてこは動かず、つりあうことになります。
静止している物体や等速で動いている物体というのは必ずこの力のモーメントがつりあっています。
つまり下図で以下のような式が成り立ちます。
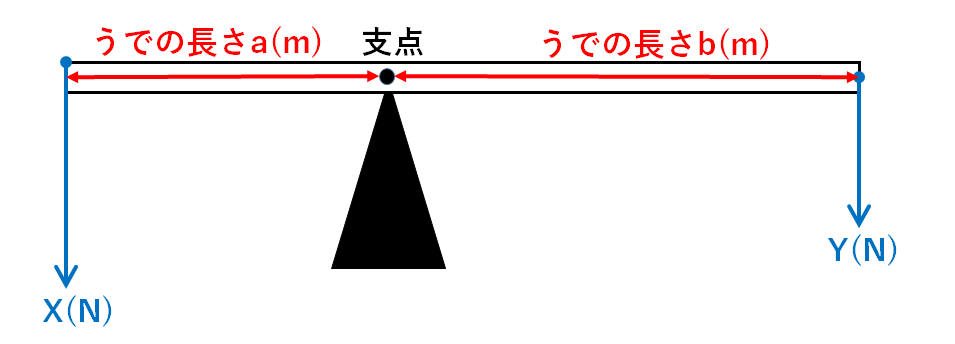
▼力のモーメントのつり合い
X(N)×a(m)=Y(N)×b(m)
3.輪軸を使った仕事
■輪軸(りんじく)
輪軸とは次のような道具です。
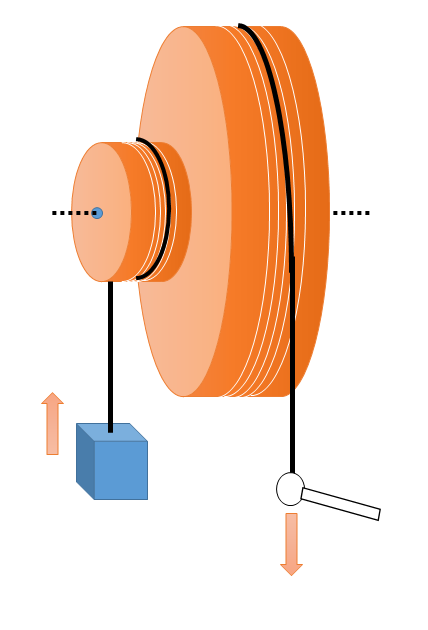
大きな輪の中心部分に小さな輪を固定して同時に回転するようにした道具です。
例題8
下図のように輪軸を使って6kgの物体を1m引き上げたい。
ただし摩擦や糸の重さは考えない。
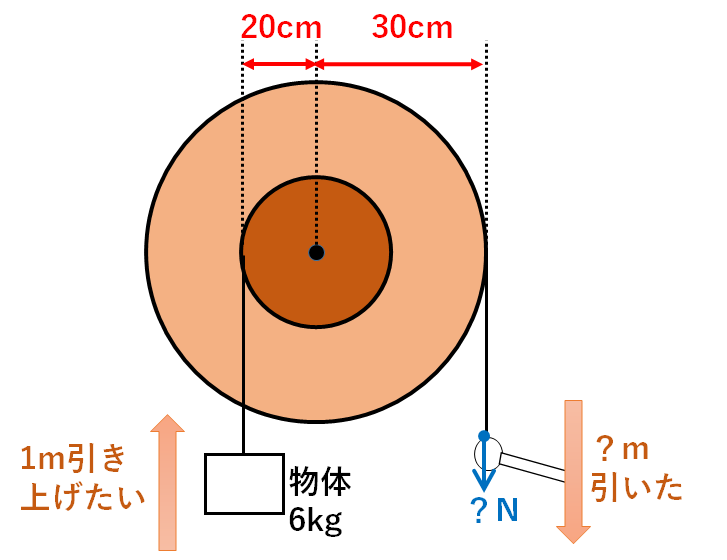
(1)右端の糸を何Nで引けばよいか。
(2)右端の糸を何m引けばよいか。
(答)
(1)
考え方はてこの場合(力のモーメント)を使うとはやいです。
輪軸を次のようなてこと考えて解いてみましょう。
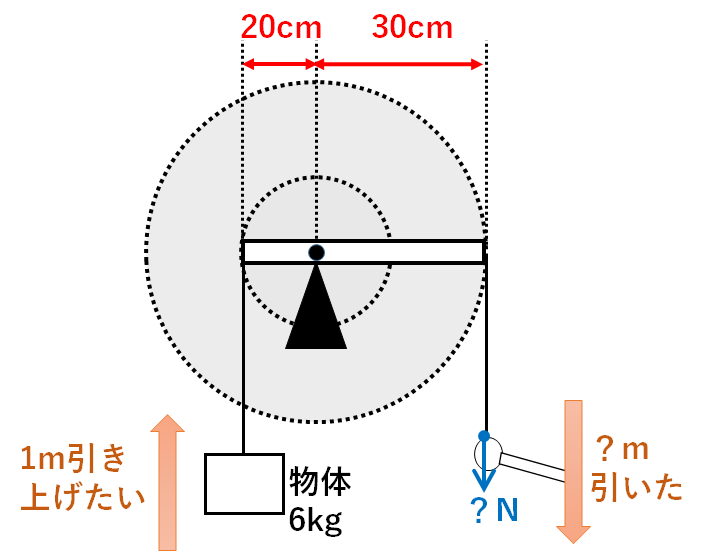
手で引いた力をx(N)と考えて
反時計回りのモーメント…60N×0.2m=12N・m
時計回りのモーメント……x(N)×0.3m=0.3x(N・m)
これらのつり合いを考えて
12N・m=0.3x(N・m)
よってx=40N
つまり40Nが正解です。
(2)
物体がされた仕事は
60N×1m=60J
一方手がした仕事は、手が糸を引いた長さをy(m)とすると
40N×y(m)=40y(J)
60J=40y(J)
なのでy=1.5m
よって1.5mが正解です。
※力のモーメントを考えなければいけない高校入試の問題は最近ではほとんどありません。有名なのはH18年度東大寺学園の「傘」の問題でしょう。興味がある人はやってみてください。

コメント(承認された場合のみ表示されます)