1.摩擦力とは
■摩擦力
物体の動こうとする向きと反対向きにはたらく力。
摩擦力は、物体と床、物体と地面など、物体どうしの接している面にはたらく力です。
その向きは物体の動こうとする向きと反対向きです。
感覚として
・「ざらざらな面」は摩擦力が強くはたらく。
・「つるつるな面」は摩擦力があまりはたらかない。(氷の上など)
と思っていればいいでしょう。
※実際には摩擦力の大きさは垂直抗力の大きさに比例します。
■摩擦がする仕事
摩擦力は物体の動きをジャマする力とも言えるでしょう。
摩擦力がはたらくからこそ、摩擦のある面上で動いている物体は最終的には止まってしまいます。
止まる=速さがゼロ=運動エネルギーが0J
ということです。
摩擦力は運動エネルギーをうばうことができる=摩擦が仕事をする
ということでもあります。
※エネルギーについては→【力学的エネルギーの保存】←を参考に。
※仕事については→【仕事の基本】←を参考に。
2.摩擦力を求める問題
次のような2問の例題を見てみましょう。
例題1
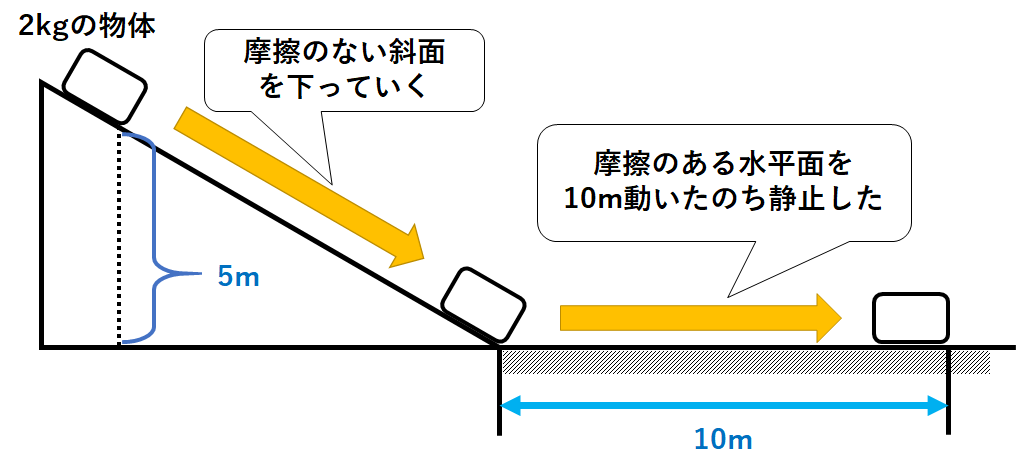
2kgの物体を↓の図のような斜面から静かにすべらせた。
物体は斜面をすべりおりて、水平面を10m進んで静止した。
この斜面には摩擦力がはたらかないが、物体には摩擦がはたらく。
このとき水平面上で物体にはたらいた摩擦力は何Nか。
ただし100gの物体にはたらく重力を1Nとする。
(答)
摩擦の仕事によってエネルギーをうばわれる典型的な例題です。
まずスタート地点での位置エネルギーを求めましょう。
$$位置エネルギー=重さ(N)×高さ(m)$$
で求められますので
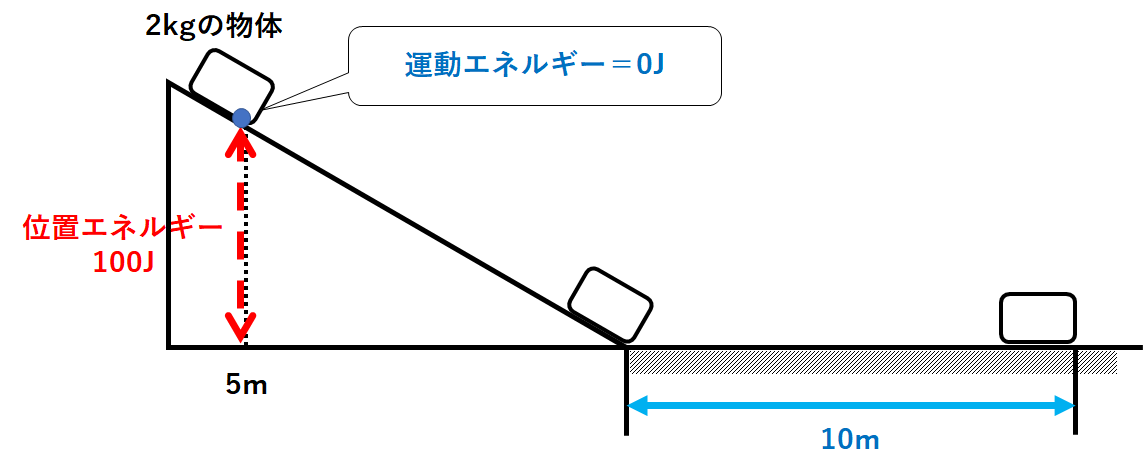
$$位置エネルギー=20N×5m=100J$$
です。(↓の図)
次にスタート地点での運動エネルギーを考えます。
静かに手をはなす=速さを与えないということなので
$$速さ=0m/s$$
です。
よって運動エネルギーも
$$運動エネルギー=0J$$
となります。(↓の図)
力学的エネルギーを考えましょう。
$$力学的エネルギー=位置エネルギー+運動エネルギー(和)$$
ですので、今の場合
$$$力学的エネルギー=100J$$
となります。(↓の図)
これが力学的エネルギーの保存により、斜面の最下点まで保存されます。
しかし水平面を進んでいるときは
摩擦力がはたらくため力学的エネルギーは保存されない
ということになります。
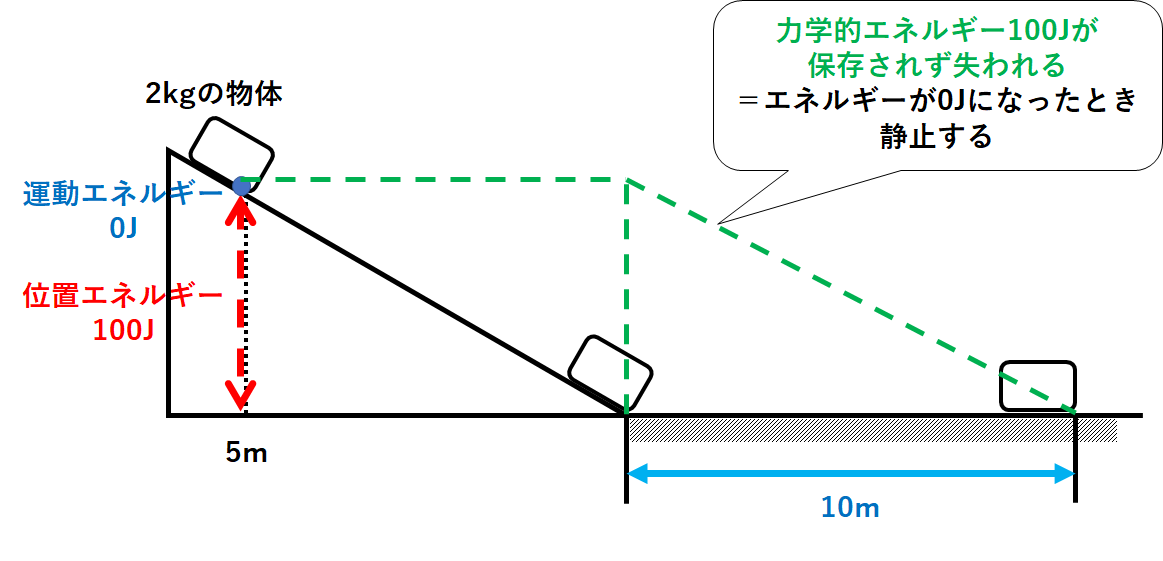
静止した地点では
$$位置エネルギー=0J$$
$$運動エネルギー=0J$$
なので
$$力学的エネルギー=0J$$
となっています。
つまり摩擦力によって100Jの力学的エネルギーは失われたのです。
言い換えると摩擦力は100Jの仕事をしたのです。(↓の図)
仕事の求め方は
$$仕事(J)=力(N)×力の向きに動いた距離(m)$$
です。
摩擦力をx(N)とすると
$$摩擦のした仕事=x(N)×10(m)=10x(J)$$
となります。
これが失われた力学的エネルギー100Jに等しいので
$$10x(J)=100(J)$$
よってx=10Nとなります。
つまり摩擦力は10Nとなります。
例題2
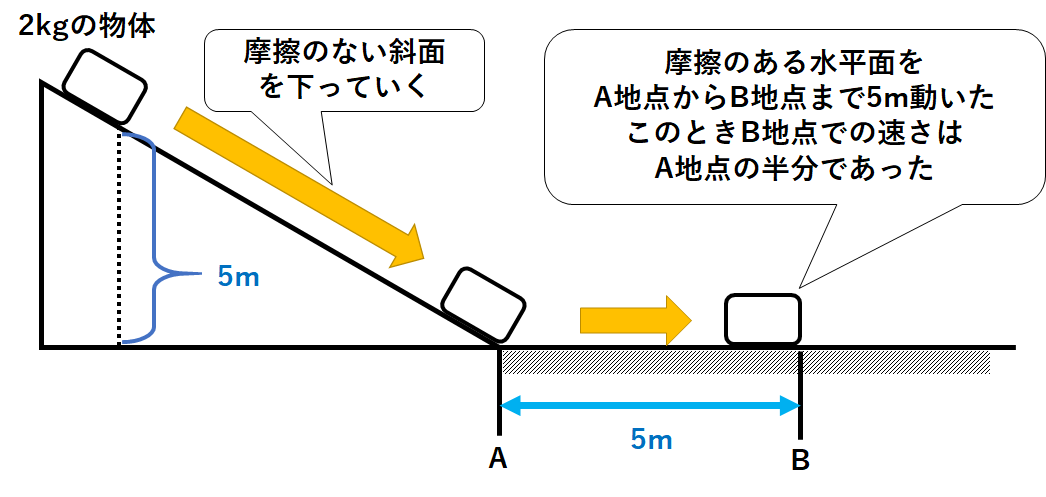
2kgの物体を↓の図のような斜面から静かにすべらせた。
物体は斜面をすべりおりて、A点に達したのち5mはなれたB点を通過した。
B点での速さはA点での速さの2分の1であった。
この斜面には摩擦力がはたらかないが、物体には摩擦がはたらく。
このとき水平面上で物体にはたらいた摩擦力は何Nか。
ただし100gの物体にはたらく重力を1Nとする。
(答)
先ほどと同じ、摩擦の仕事によってエネルギーをうばわれる例題です。
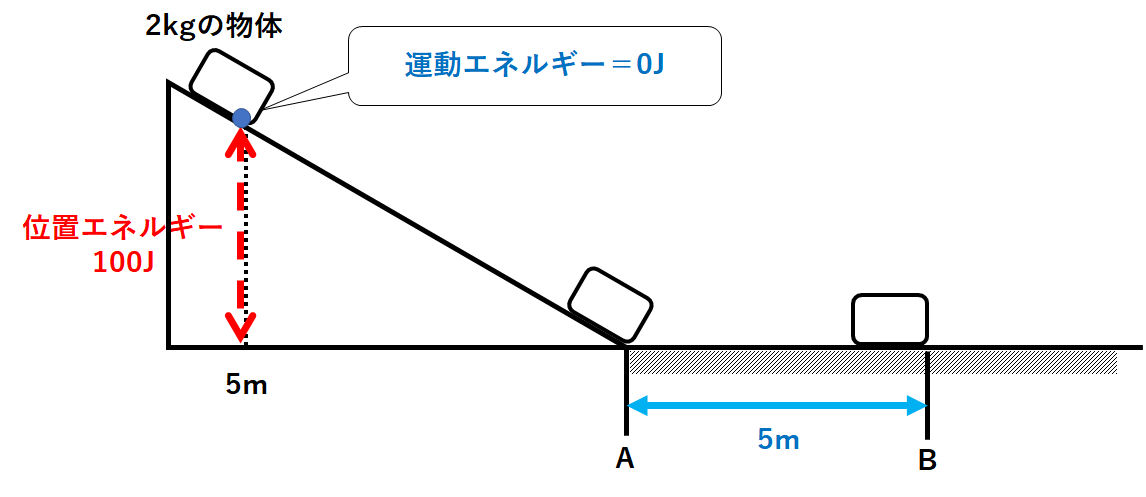
まずスタート地点での位置エネルギーを求めましょう。
$$位置エネルギー=重さ(N)×高さ(m)$$
ですから
$$位置エネルギー=20N×5m=100J$$
です。(↓の図)
次にスタート地点での運動エネルギーを考えます。
静かに手をはなす=速さを与えないということなので
$$速さ=0m/s$$
です。
よって運動エネルギーも
$$運動エネルギー=0J$$
となります。(↓の図)
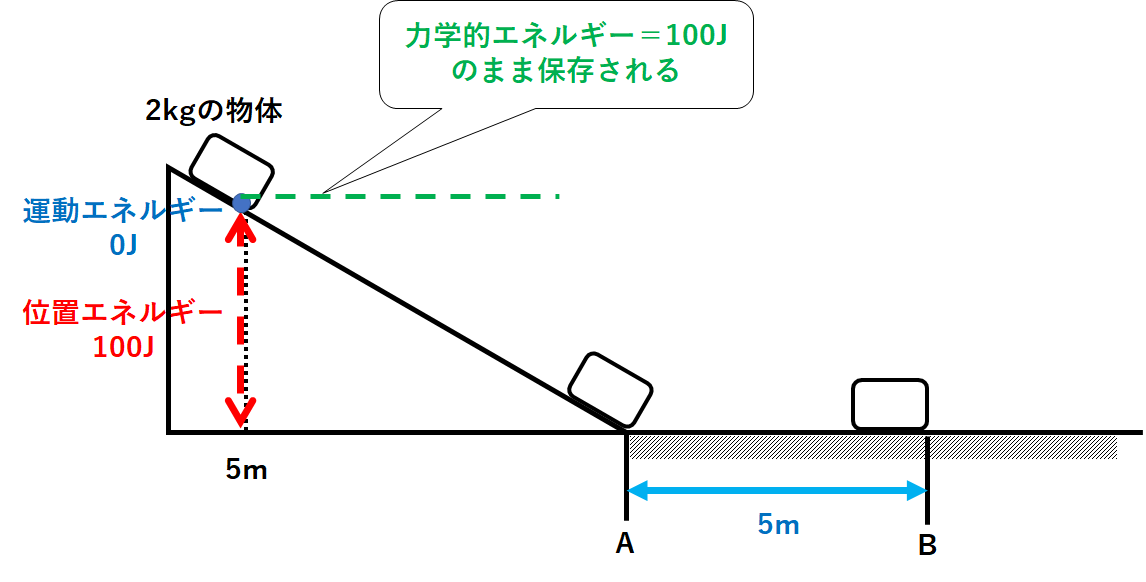
力学的エネルギーを考えましょう。
$$力学的エネルギー=位置エネルギー+運動エネルギー(和)$$
ですので、今の場合
$$$力学的エネルギー=100J$$
となります。(↓の図)
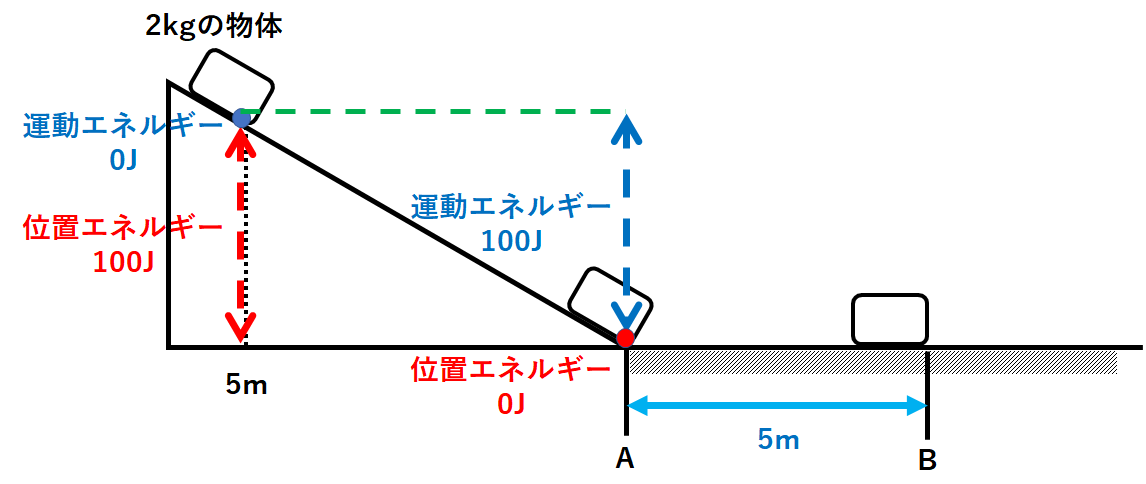
これが力学的エネルギーの保存により、斜面の最下点であるA点まで保存されます。
よってA点では
$$位置エネルギー=0J$$
$$運動エネルギー=100J$$
です。(↓の図)
しかし水平面を進んでいるときは
摩擦力がはたらくため力学的エネルギーは保存されない
ということになります。
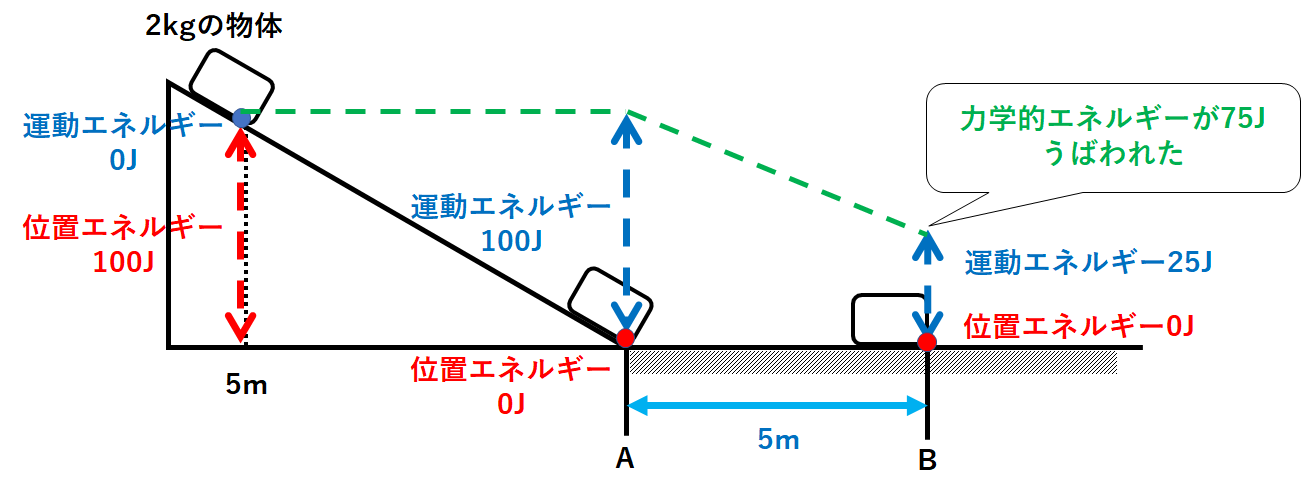
今の場合、B点を通過するときに速さが減っているので運動エネルギーが失われていることになります。
ではB点でのエネルギーを考えましょう。
B点では
$$位置エネルギー=0J$$
です。
次にB点の運動エネルギーを考えます。
運動エネルギーは速さの2乗に比例します。
速さの2乗に比例とは・・・
速さが2倍・3倍・4倍になると、運動エネルギーは4倍・9倍・16倍になるということです。
いまB点での速さはA点での速さの2分の1倍です。
速さが
$$ \frac{1}{2}倍$$
ということは・・・
運動エネルギーは
$$ \frac{1}{4}倍$$
ということです。
よってB点の運動エネルギーは
$$運動エネルギー=100J×\frac{1}{4}=25J$$
となります。
よってB点での力学的エネルギーは
$$力学的エネルギー=25J$$
です。(↓の図)
つまり摩擦により
$$100J-25J=75J$$
のエネルギーをうばわれた(仕事をされた)ということです。(↓の図)
摩擦力をx(N)とすると、摩擦のした仕事は
$$摩擦のした仕事=x(N)×5(m)=5x(J)$$
となります。
これが失われた力学的エネルギー75Jに等しいので
$$5x(J)=75(J)$$
よってx=15Nとなります。
つまり摩擦力は15Nとなります。
POINT!!
・摩擦力はその物体の進行方向・回転方向と反対向きにはたらく。
・摩擦力がはたらくとき、力学的エネルギーは保存されない。
・摩擦がした仕事=失われた力学的エネルギーとなる。





コメント(承認された場合のみ表示されます)
摩擦力と物体を引く力が等しいのはなんでなのですか。
結衣菜様
コメントありがとうございます。
確かに、止まっている物体を動かす瞬間は、摩擦力より大きな力で引く必要があります。
その後、動き出してからは、物体を一定の速さで動かす限りは、摩擦力と物体を引く力は一定です。
速さを変化させる(止まっているものを動かすなど)ときは、引く力>摩擦力です。
一定の速さで動かし続けるときは、引く力=摩擦力です。(等速直線運動の条件)