1.中和の量的関係(計算問題)
酸とアルカリがどのような比で混ぜ合わせたときに中性になるのかを必ず調べる。
その比に基づいて計算を行う。
例題1
(1)塩酸A 200cm3を中性にするために必要な水酸化ナトリウム水溶液Bはいくらか。
(2)水酸化ナトリウム水溶液B 7.5cm3を中性にするために必要な塩酸Aはいくらか。
(3)塩酸A 150cm3と水酸化ナトリウム水溶液B 120cm3を混ぜたときの液性は酸性・アルカリ性のどちらか。
(4)(3)でできた混合溶液を中性にするためには、塩酸Aまたは水酸化ナトリウム水溶液Bのどちらをいくら加えればよいか。
例題1の答えと解説
考え方は
→【定比例の法則】←や→【気体の発生(定比例の法則)】←と同じです。
まず
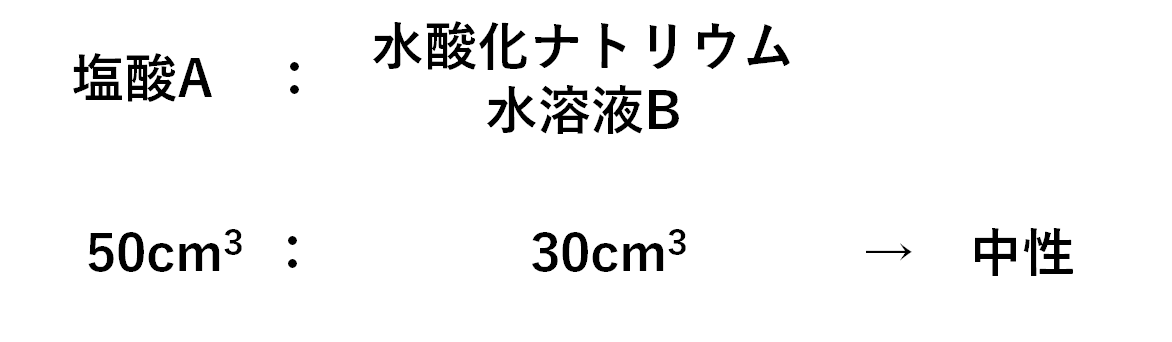
「ある濃度の塩酸A 50cm3に水酸化ナトリウム水溶液B 30cm3加えると中性になった。」
という文章から
塩酸A:水酸化ナトリウム水溶液B=50cm3:30cm3
の比で中性になることがわかります。
(1)
求める水酸化ナトリウム水溶液Bの量をx(cm3)とすると
塩酸A:水酸化ナトリウム水溶液B=50:30の比で中性になるので
$$50:30=200cm^3:x(cm^3)$$
という比例式がつくれます。これを解いて
$$x=120$$
よって120cm3が正解です。
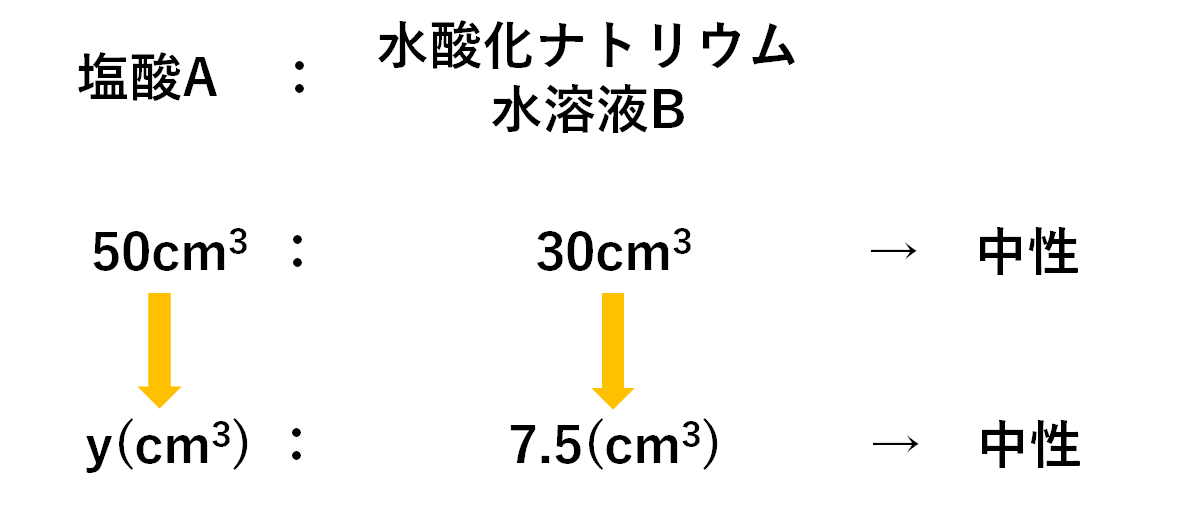
(2)
求める塩酸Aの量をy(cm3)とすると
塩酸A:水酸化ナトリウム水溶液B=50:30の比で中性になるので
$$50:30=y(cm^3):7.5 cm^3$$
という比例式がつくれます。これを解いて
$$y=12.5$$
よって12.5cm3が正解です。
(3)
問題の解説に行く前に・・・
あるうどん屋さんのお話。
そのうどん屋さんではかけうどんが売られています。
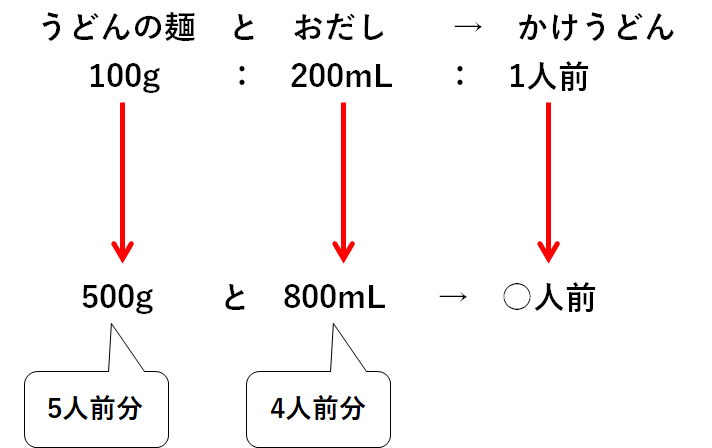
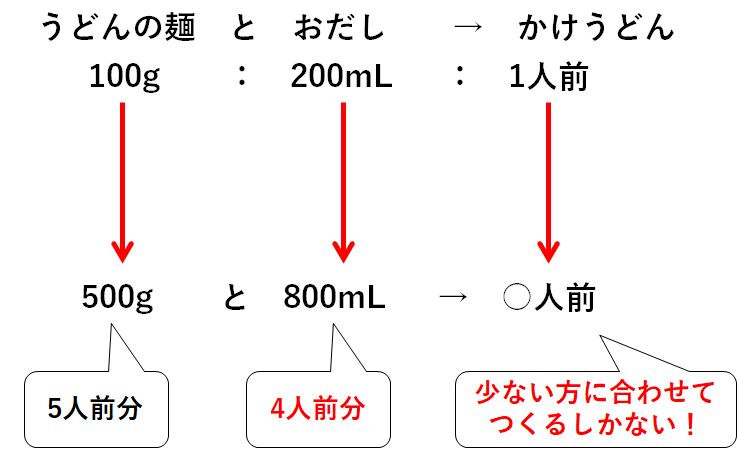
そのかけうどん1人前をつくるには、うどんの麺100gとおだし200mLが必要です。
いま、冷蔵庫を見てみるとうどんの麺が500g、おだしが800mLありました。
さあ何人前のかけうどんをつくれますか?
うどんの麺は500g、つまり5人前分あります。
おだしは800mL、つまり4人前分あります。
・うどんの麺500gをすべて使う→おだしが足りないので5人前もつくれない。
・おだし800mLをすべて使う→4人前のかけうどんしかつくれない。
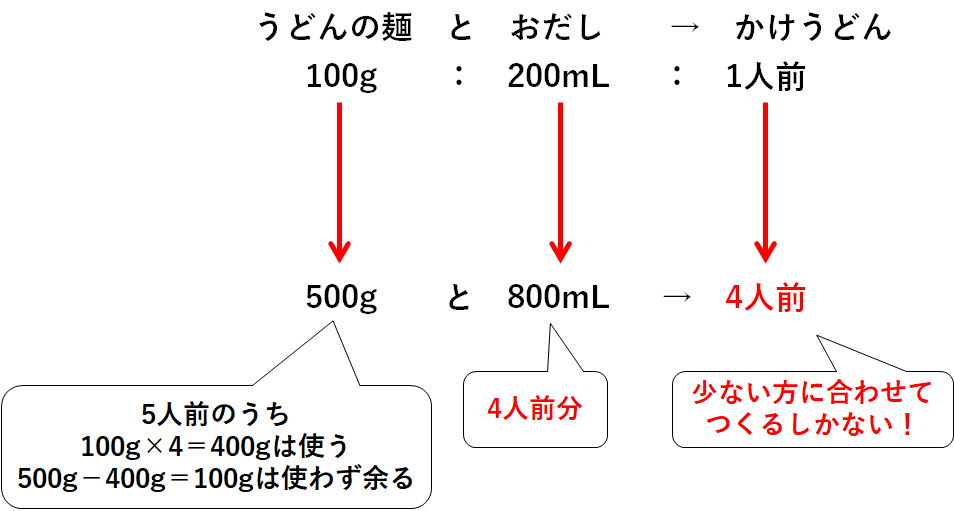
つまり最大で4人前までしかつくれないのです。
うどんの麺とおだし、少ない方に合わせて作るしかないのです。
ちなみにうどんの麺は一部が余ってしまいます。
中和の計算でも同じことを考えます。
この問題では中性にするためには
塩酸Aが50cm3・水酸化ナトリウム水溶液Bが30cm3
必要なのです。
麺 → 塩酸A
おだし→水酸化ナトリウム水溶液B
と置き換えて考えましょう。
では、この問いのように
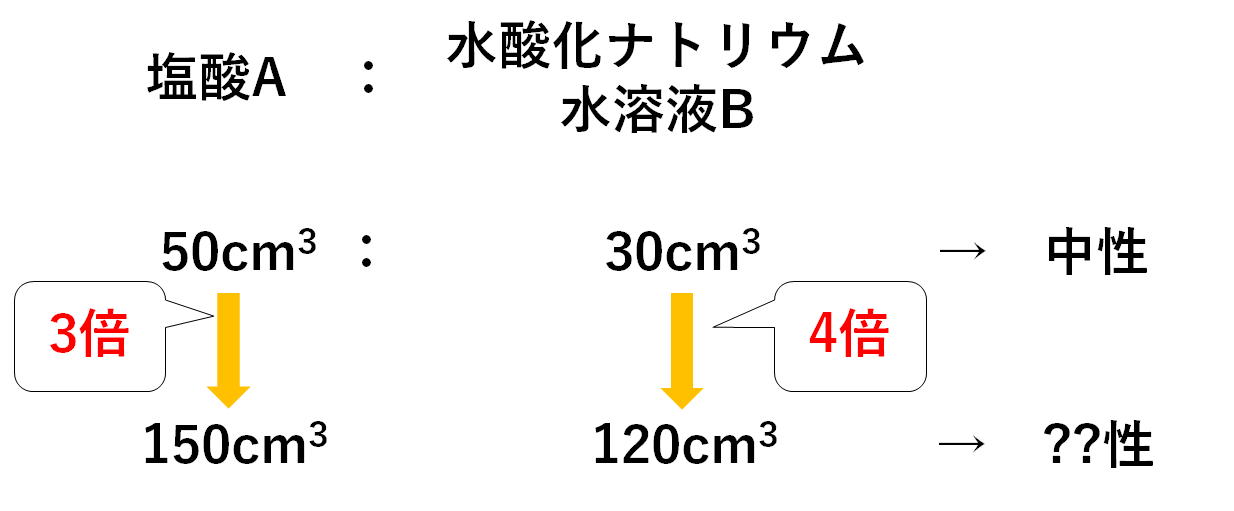
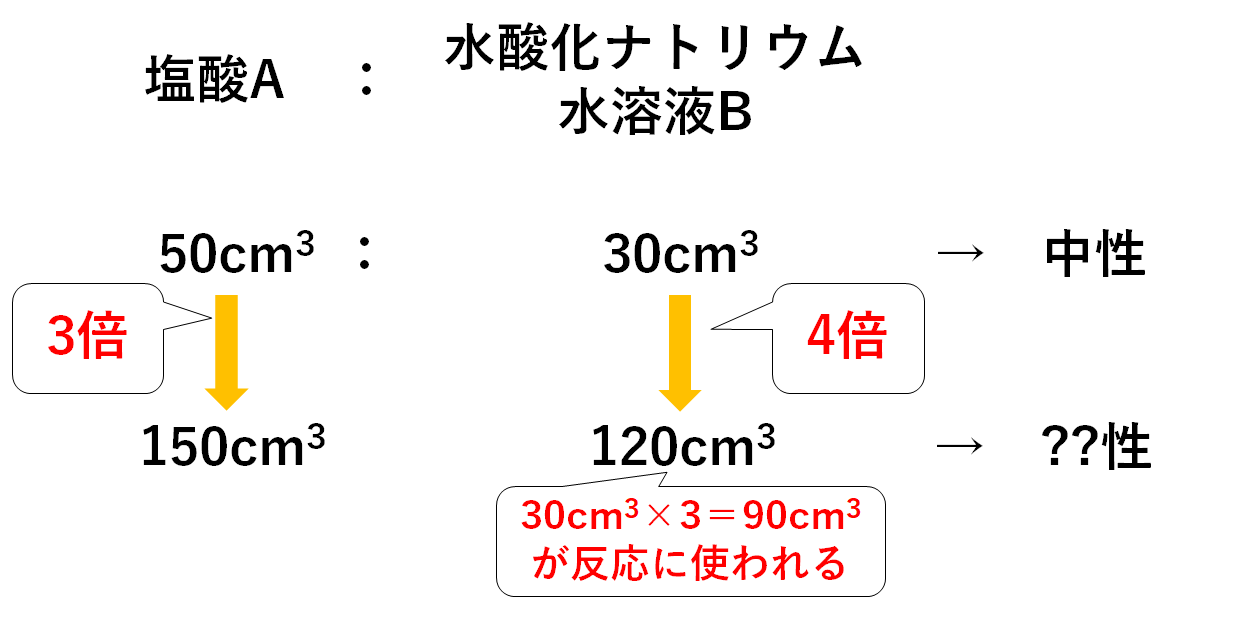
塩酸A 150cm3と水酸化ナトリウム水溶液B 120cm3
を混ぜ合わせたときは・・・
麺(塩酸A)が3人前・おだし(水酸化ナトリウム水溶液B)が4人前あるのです。
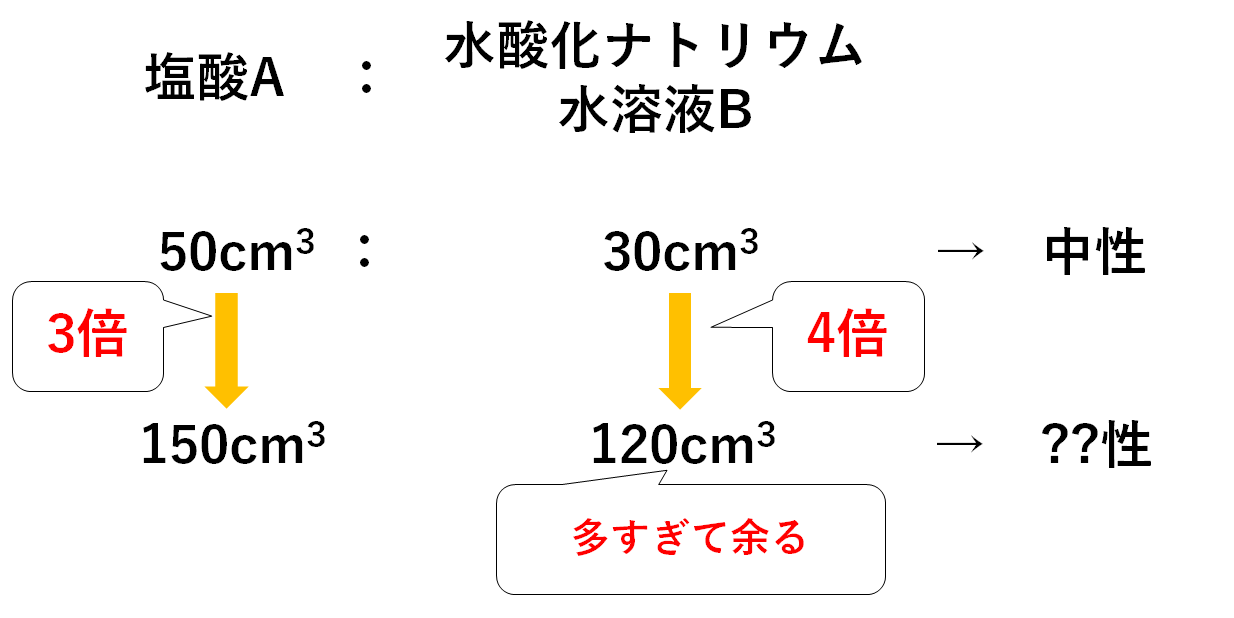
ということはおだし(水酸化ナトリウム水溶液B)が多すぎますね。
よってこの混合溶液は、
水酸化ナトリウム水溶液Bが余っている
のでアルカリ性を示すことになります。
(4)
(3)より水酸化ナトリウム水溶液Bが余ることがわかりました。
ではいくら余るかを求めましょう。
麺(塩酸A)が3人前・おだし(水酸化ナトリウム水溶液B)が4人前あると思うと・・・
おだし(水酸化ナトリウム水溶液B)は
$$30cm^3×3=90cm^3$$
使われることになります。
もともとある水酸化ナトリウム水溶液Bは120cm3です。
よって反応せず余る水酸化ナトリウム水溶液Bは
$$120cm^3-90cm^3=30cm^3$$
となります。
この水酸化ナトリウム水溶液Bの余り30cm3を中和すれば、混合溶液全体が中性になります。
つまり加えるべきは塩酸Aです。
塩酸Aをz(cm3)加えるとすると
$$50:30=z(cm^3):30(cm^3)$$
という比例式となります。これを解いて
$$z=50$$
よって塩酸Aを50cm3加えればよいということになります。
POINT!!
・中和の計算問題は、化学変化の問題と同じ。
→ ” 中性になるときの 酸の量:アルカリの量の比 ” を求めておく。
・過不足のある問題では、小さい方の倍率に合わせて計算する。
2.電流のグラフの読み取り
例題2
このビーカーに少しずつ水酸化ナトリウム水溶液Dを加えていく。
このときの色の変化と混合液がどれだけ電流を通すかを測定した。
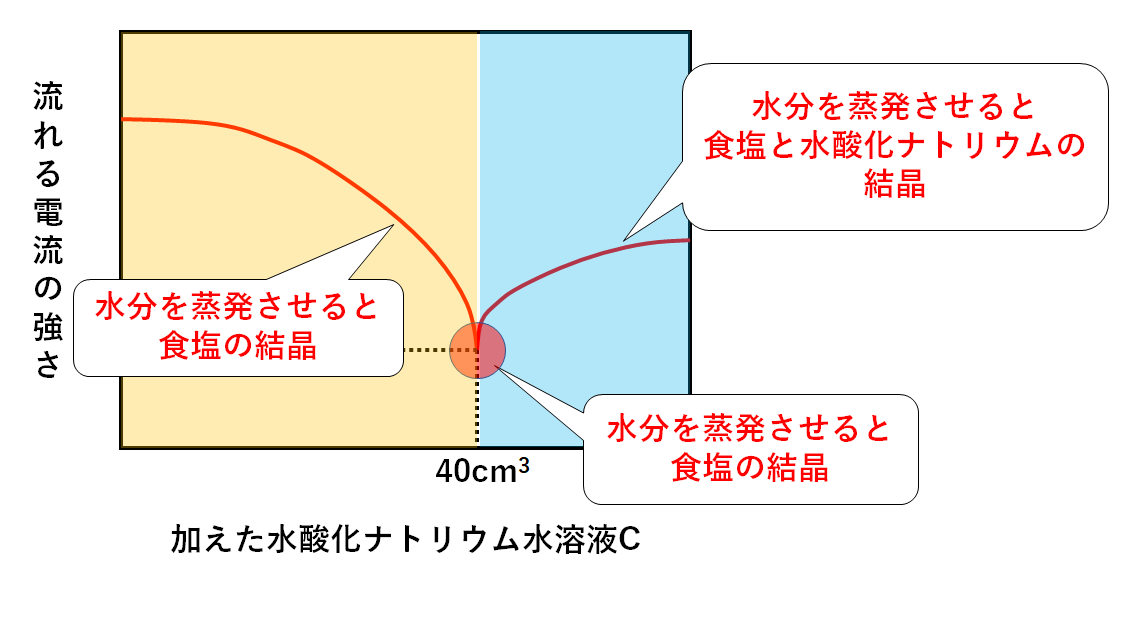
次のグラフは加えた水酸化ナトリウム水溶液Dと混合液に流れた電流の強さとの関係を表したグラフである。
うすい塩酸C 250cm3を中性にするには水酸化ナトリウム水溶液Dがいくら必要か。
例題2の答えと解説
このグラフの意味を理解しておきましょう。
まず、中性のときはイオンがもっとも少ないです。(イオン濃度が最も低い)
そのため電流が最も流れにくいわけです。
言い換えると
電流が最も流れにくいところ・・・中性である
です。
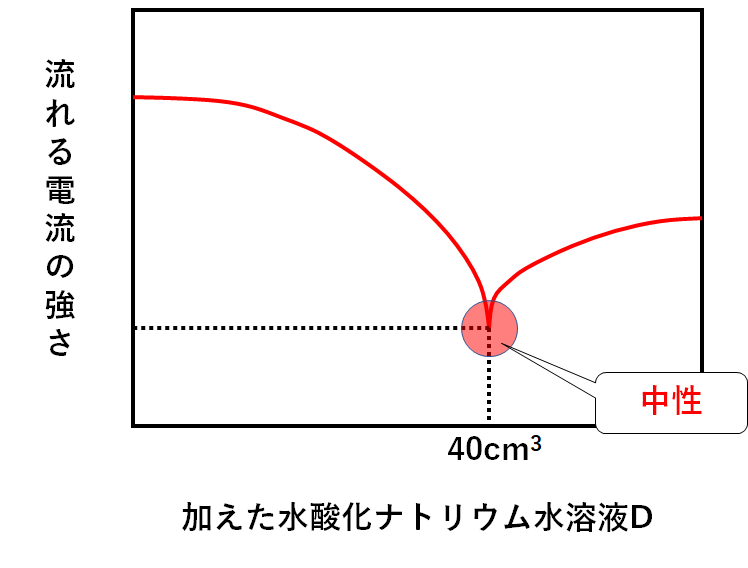
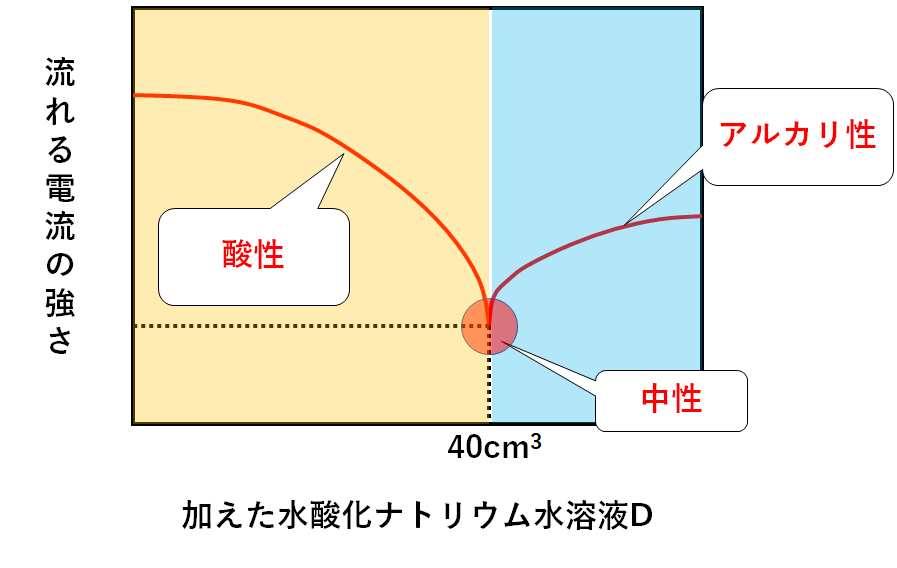
この問いの場合、水酸化ナトリウム水溶液Dを40cm3加えたところで中性に達したわけです。(↓の図)
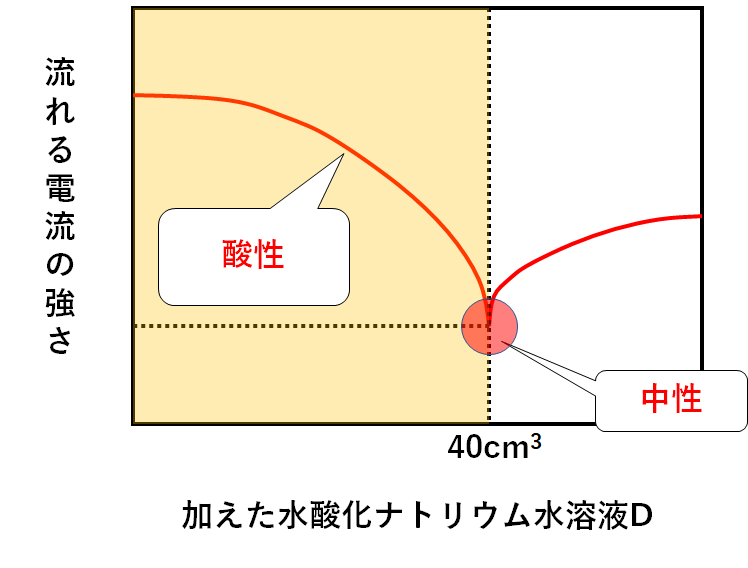
では40cm3よりも少ない量の水酸化ナトリウム水溶液Dを加えたときは・・・
中性に達していない、ということです。
まだ中和されていない塩酸が残っている状態です。
塩酸が残っている=溶液全体として酸性です。(↓の図)
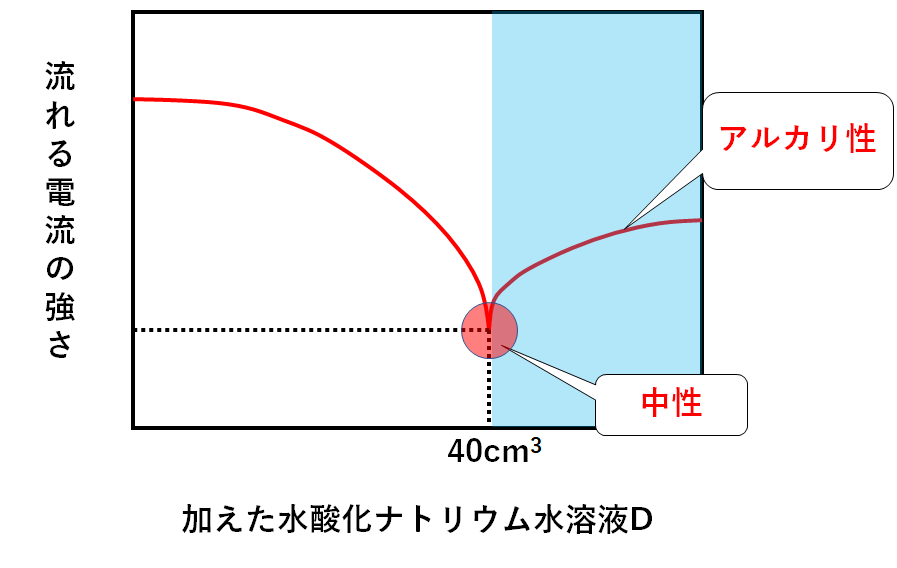
また40cm3よりもたくさんの量の水酸化ナトリウム水溶液Dを加えたときは・・・
水酸化ナトリウム水溶液Dを入れ過ぎて、中性を飛び越えてしまっています。
つまり水酸化ナトリウム水溶液Dが多すぎて残っているのです。
水酸化ナトリウム水溶液が多すぎて残っている=溶液全体としてアルカリ性、ということです。(↓の図)
まとめると↓のようになります。
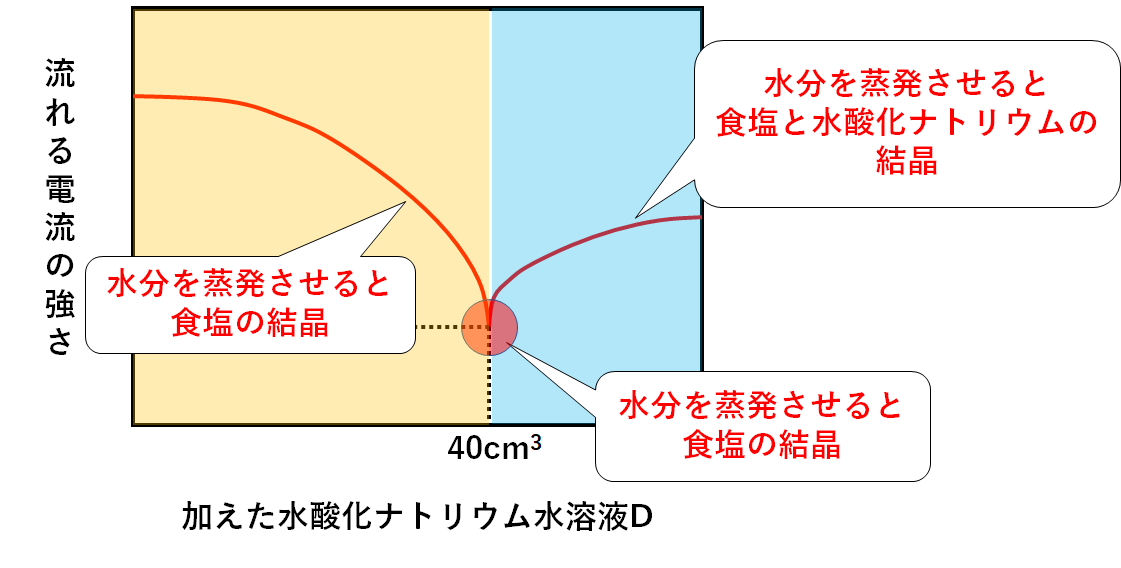
ちなみに各部分の溶液を蒸発皿に入れ、水分を蒸発させると・・・
酸性の部分・・・・・・中和で生じた食塩が結晶として現れます。
中性の部分・・・・・・中和で生じた食塩が結晶として現れます。
アルカリ性の部分・・・中和で生じた食塩に加えて、反応せずに余っている水酸化ナトリウムも結晶として現れます。(↓の図)
※食塩と塩化ナトリウムは同じ物質のこと。
本題にもどりましょう。
このグラフから
塩酸C:水酸化ナトリウム水溶液D=100cm3:40cm3
の比で中性になることがわかります。
よって求める水酸化ナトリウム水溶液Dをx(cm3)とすると
$$100:40=250cm^3:x(cm^3)$$
という比例式がつくれます。これを解いて
$$x=100$$
水酸化ナトリウム水溶液Dを100cm3加えればよいというのが正解です。
POINT!!
・中性のとき、もっとも電流が流れにくい!




コメント(承認された場合のみ表示されます)