このページは化学変化の計算問題の典型的な応用問題である「未反応」「混合物」の解き方を解説しています。
動画による解説は↓↓↓
チャンネル登録はこちら↓↓↓
基本的な化学変化の計算については
→【質量保存の法則】← または →【定比例の法則(酸化)】←
で解説しています。
1.定比例の法則の応用問題
銅の酸化とマグネシウムの酸化を例にして化学の典型的な計算問題について紹介しました。
化学変化の計算問題では
・何と何が反応して何ができるかをチェック(反応のようす)
・その反応の質量比を求めておく
・その比をもとに比例式をつくる
という3ステップで解いていくのが重要です。
しかし、単純に比例式をつくるだけでは解けない問題もあります。
このページでは、その中でも代表的な【未反応のものがある問題】と【混合物の問題】を紹介します。
1.未反応のものがある問題
例題1
(2) 6gのマグネシウムを燃焼したところ加熱が不十分であったため質量が7.5gになった。まだ反応していないマグネシウムは何gか。
例題1の答えと解説
この問題文からわかること。
それはすべての銅またはマグネシウムが反応したわけではなく一部が未反応であるということです。
この「未反応の物質が存在する問題」は定番の問題です。
解き方が決まっていますのでしっかりできるようにしてください。
(1)
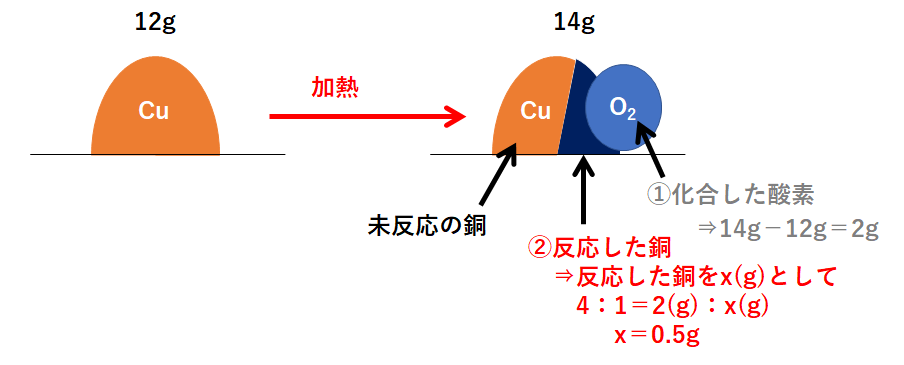
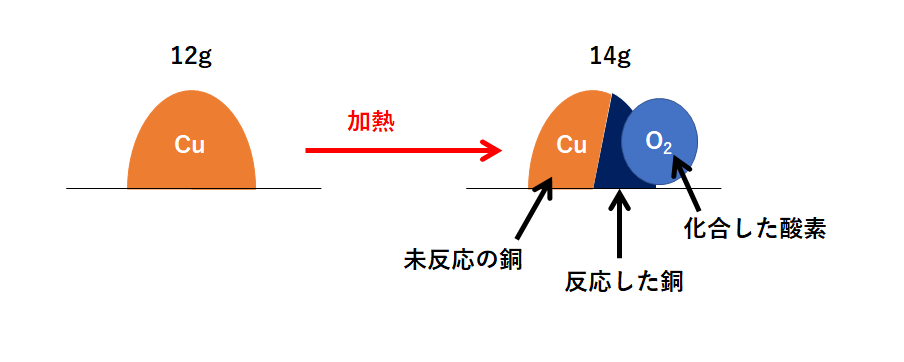
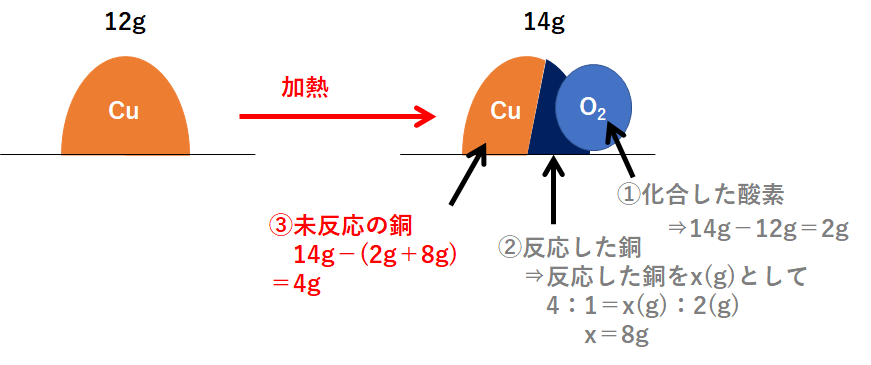
この問題の状況を図に表しました。
右側が反応後を表していますが、右側の図は3つの部分に分かれます。
「①化合した酸素」「②反応した銅」「③未反応の銅」
です。
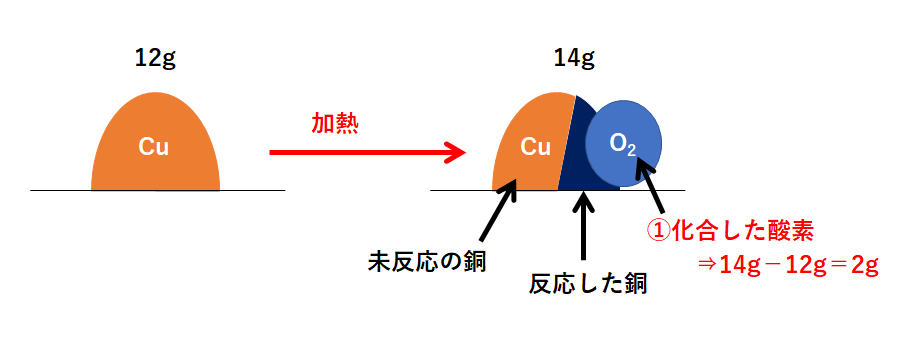
まず「①化合した酸素」から求めます。
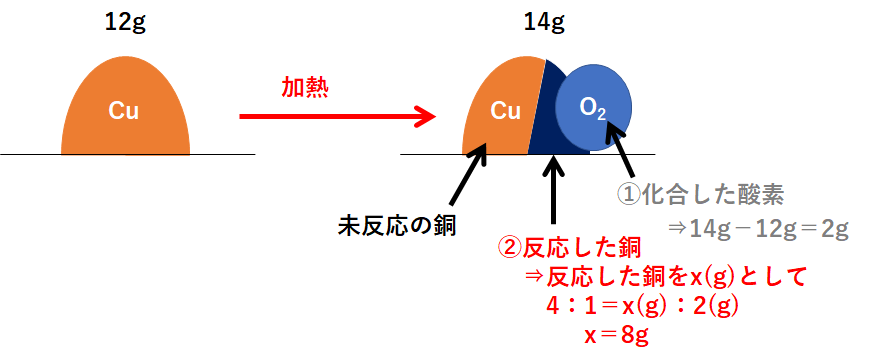
次に「②反応した銅」です。
そして最後に「③未反応の銅」を求めましょう。
必ずこの①~③の順で解きます。
よって 4g となります。
<<別解>>
連立方程式を用います。
反応した銅を x(g)、反応しなかった銅を y(g)としましょう。
はじめ銅全部で 12g あるので
$$x+y=12・・・①$$
と表すことができます。
反応後、銅 x(g)は酸化銅へと変化します。
その量は4:5。
もとの銅の 5/4倍(4分の5倍) です。
反応後では反応していない銅が y(g) あるので
$$\frac{5}{4}x+y=14・・・②$$
①②を解いて
$$x=8 y=4$$
となり
未反応の銅は4gとなります。
(2)
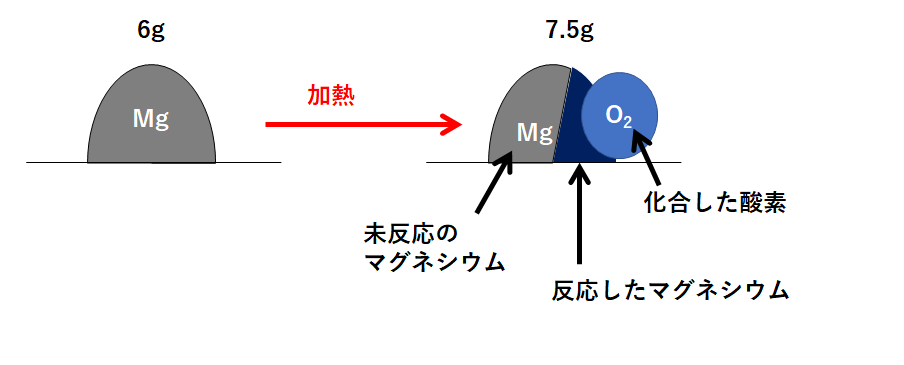
(1)と同じように、この問題の状況を図に表しました。
先ほどと同様、反応後の図(右側)には
「①化合した酸素」「②反応したマグネシウム」「③未反応のマグネシウム」
の3つの部分があります。
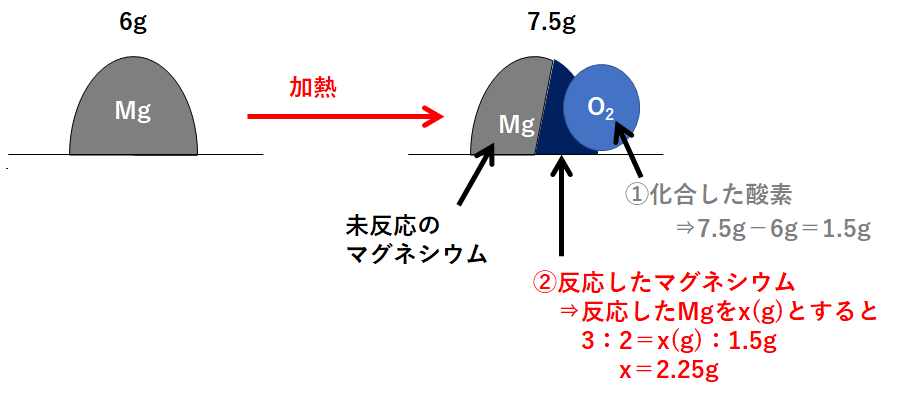
まず「①化合した酸素」から求めます。
次に「②反応したマグネシウム」です。
そして最後に「③未反応のマグネシウム」を求めましょう。
必ずこの①~③の順で解きます。
よって3.75gとなります。
<<別解>>
先ほどの別解と同様、連立方程式を用います。
反応したマグネシウムを x(g) 、反応しなかったマグネシウムを y(g) としましょう。
はじめマグネシウム全部で 6g あるので
$$x+y=6・・・①$$
と表すことができます。
反応後、マグネシウム x(g) は酸化マグネシウムへと変化します。
その量は3:5。
もとの銅の 5/3倍(3分の5倍) です。
反応後では反応していない銅がy(g)あるので
$$\frac{5}{3}x+y=7.5・・・②$$
①②を解いて
$$x=2.25 y=3.75$$
となり、
未反応のマグネシウムは3.75gとなります。
未反応のものがある問題では・・・
・図を書いて「酸素」→「酸素と反応した部分」という順序で求めていく
・反応したものをx(g)、反応しなかったものをy(g)として連立方程式のいずれかで解こう。
2.混合物を反応させている問題
例題2
これを完全に酸化させると質量は7.5gになった。
はじめ銅とマグネシウムは何gずつあったか。
例題2の答えと解説
これも典型的な「混合物」の問題です。
この問題は
はじめの銅とマグネシウムの質量をx(g)、y(g)とおいて連立方程式をつくる
が最もポピュラーな解き方です。
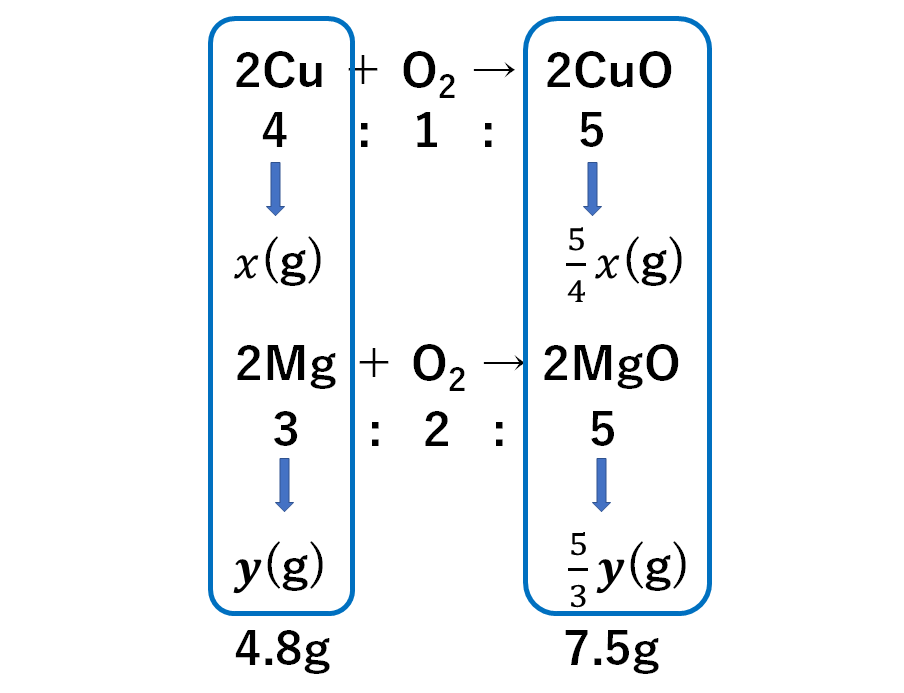
はじめの銅とマグネシウムの質量をx(g)、y(g)とおくと
生じる酸化銅、酸化マグネシウムの質量は↓のように表されます。
もとの問題の条件をあてはめて
次のような連立方程式をつくります。
$$x+y=4.8$$
$$\frac{5}{4}x+\frac{5}{3}y=7.5$$
これを解いて
$$x=1.2 y=3.6$$
となります。
よって銅 1.2g マグネシウム 3.6g が正解です。
POINT!!
混合物の問題では
一方の物質を x(g) 、もう一方の物質を y(g) として
反応前で式を1つ、反応後で式をもう1つつくる。
その連立方程式を解く。
※ここでは銅とマグネシウムでの【未反応のものがある問題】【混合物の問題】を紹介しました。
が、実際の入試問題では異なる物質の反応の場合も多いです。
しかし解き方は変わりませんので、見た目に惑わされず計算してください。



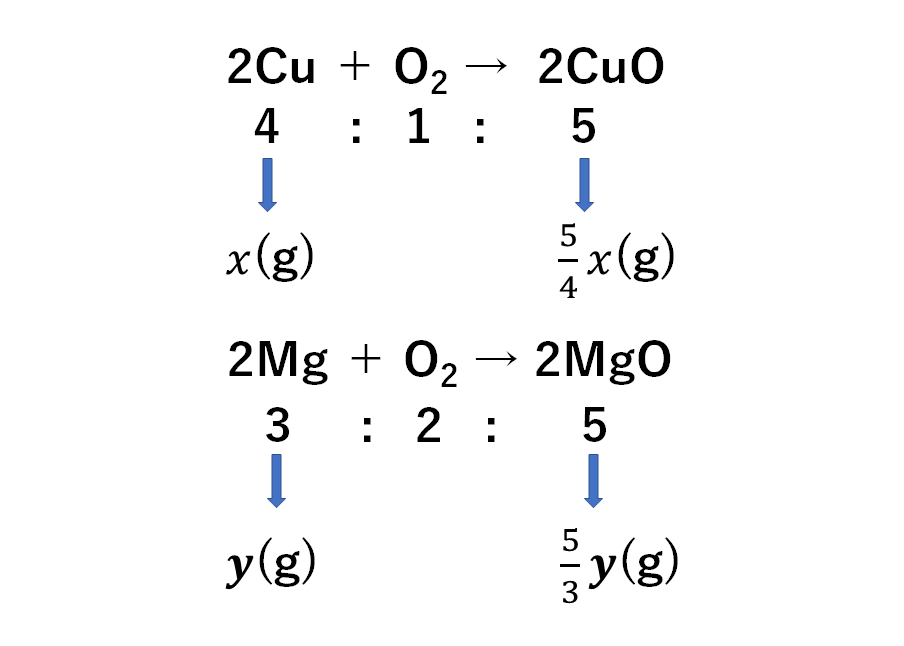
コメント(承認された場合のみ表示されます)
4:1とか3:2とかの質量比は、どこから出て来るのか?説明が足りなくないか?
匿名様
コメントありがとうございます。
貴重なご意見ありがとうございます。
まず化学変化では物質は決まった比で反応します。
例えば銅の酸化では銅:酸素:酸化銅=4:1:5で反応します。
マグネシウムの酸化ではマグネシウム:酸素:酸化マグネシウム=3:2:5です。
これは問題でグラフや表が与えられるのでそこから求めることができますが、必ずこの比なので覚えた方が早いです。
このページは「応用」と本文中で書いてあるため、こちらの解説は省いております。
詳細な解説は、本文にもリンクがありますが
よりご覧ください。
高校受験を控える中3です。
すごく分かりやすくて助かりました!ありがとうございましたm(_ _)m
コメントありがとうございます。
お役に立てて何よりです。
受験勉強は大変だと思いますが、がんばってくださいね。
なぜ4/5xと3/5yになるのですか?教えていただけるとありがたいです
小林様
コメントありがとうございます。
銅4gを加熱すると酸化銅5gができます。
この量を比べると5g÷4g=5/4(4分の5倍)です。
銅x(g)を加熱すると酸化銅はx×5/4(g)となります。
マグネシウム3gを加熱すると酸化マグネシウム5gできます。
この量を比べると5g÷3g=5/3(3分の5倍)です。
マグネシウムy(g)を加熱すると酸化マグネシウムはy×5/3(g)となります。
反応前の式を
Cu+Mg=4.8
反応後の式を 増えた酸素2.7gより
1/4Cu+2/3Mg=2.7
として、連立方程式を立てても解けそうですが計算しても答えとあいません。
なぜでしょうか?
山田たろう様
コメントありがとうございます。
Cuをx(g)、Mgをy(g)とし、酸素の量に着目して立式すると
x+y=4.8・・・①
1/4x+2/3y=2.7・・・②
②の両辺を12倍すると
3x+8y=32.4・・・②’
①の両辺を3倍すると
3x+3y=14.4・・・①’
②’-①’より
5y=18
y=3.6
したがってx=1.2
となります。もう一度計算を確認していただけるでしょうか。