このページでは「輪軸を使った仕事」について解説しています。
仕事の基本的な求め方は →【仕事とは】← を参考に。
1.輪軸とは
輪軸とは↓のような道具です。
大きい輪と小さい輪を組み合わせた道具です。
直径の異なる2つの滑車を組み合わせたもの、ということもできます。
出題例
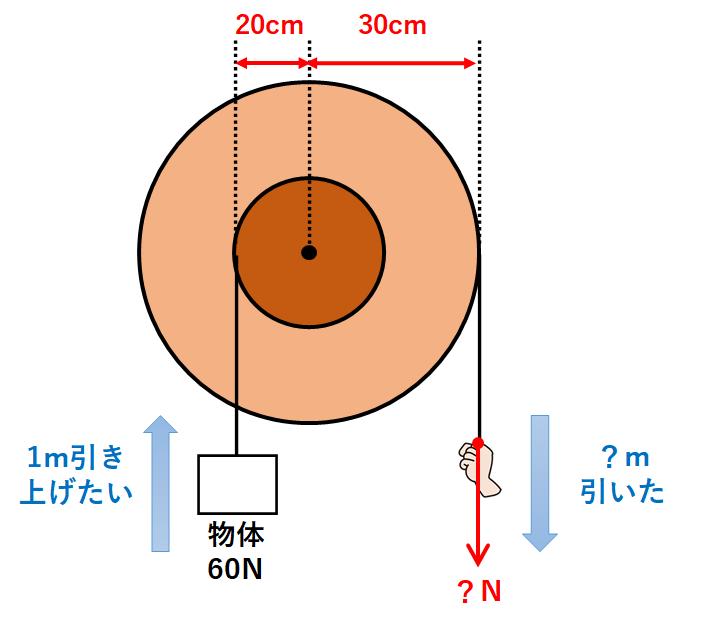
↓は輪軸を正面から見た図です。
小さい輪が半径20cm、大きい輪が半径30cmです。
小さい輪に糸で取り付けた60Nの物体を持ち上げるために、大きい輪に取り付けた糸を引っ張ります。
輪軸の考え方は“てこ”と全く同じ。
※てこを使った仕事の計算は →【てこを使った仕事】← を参考に。
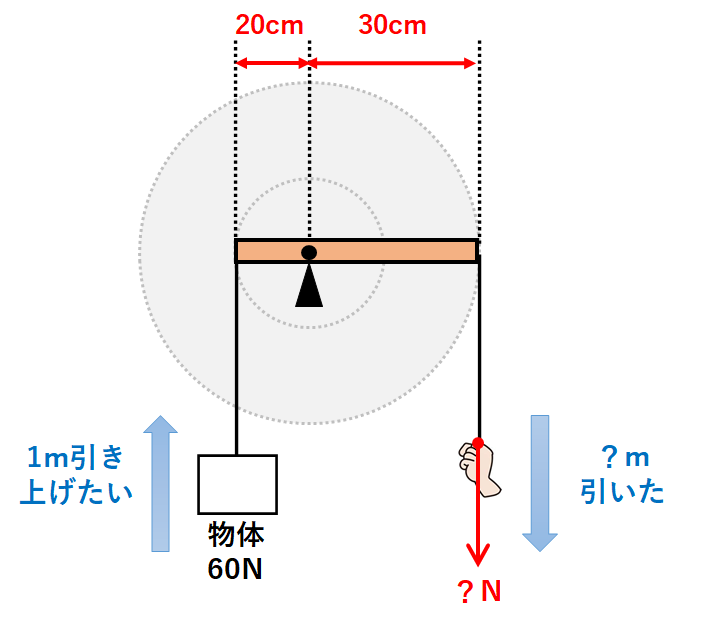
輪軸は↓のようなてこに置き換えることができます。
てこの場合は「力×うでの長さ=一定」という関係式が使えました。
手が引く力をx(N)とすると、この問題でも使えます。
支点より左側では
力×うでの長さ=60N×20cm
支点より右側では
力×うでの長さ=x(N)×30cm
これらが等しいので
60N×20cm=x(N)×30cm
これを解いてx=40N
手が引く力は40Nとわかります。
仕事は次のように求められます。
仕事=力×力の向きに動いた距離
60Nの物体を1m引き上げようとしているので
物体がされた仕事=60N×1m=60J
手が引いた距離をy(m)とすると、40Nでy(m)引いたことになるので
手がした仕事=40N×y(m)=40y(J)
これらは等しいので
40y=60
これを解いてy=1.5m
手が引いた距離は1.5mとわかります。
例題1
(答)
(1)
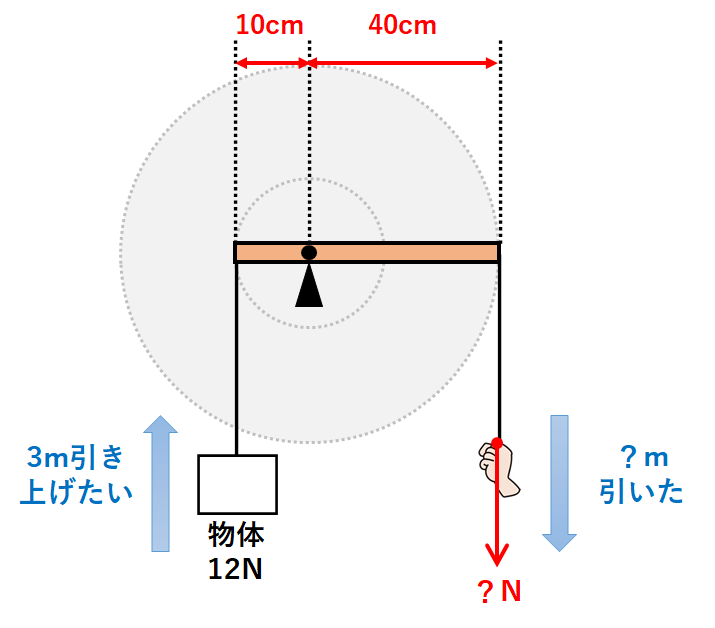
輪軸を↓のようにてこの置き換えてみましょう。
手が糸を引く力をx(N)として、力×うでの長さ=一定 であることを使います。
作用点の左側の力×うでの長さ=12N×10cm
作用点の右側の力×うでの長さ=x(N)×40cm
これらは等しいので
12N×10cm=x(N)×40cm
これを解いてx=3N
手が糸を引く力は3Nとわかります。
(2)
手が糸を引く距離をy(m)として、物体がされた仕事=手がした仕事 であることを使います。
物体がされた仕事=12N×3m=36J
手がした仕事=3N×y(m)=3y(J) ※3Nは(1)より
これらは等しいので
3y=36
これを解いてy=12m
手が糸を引く距離は12mとわかります。
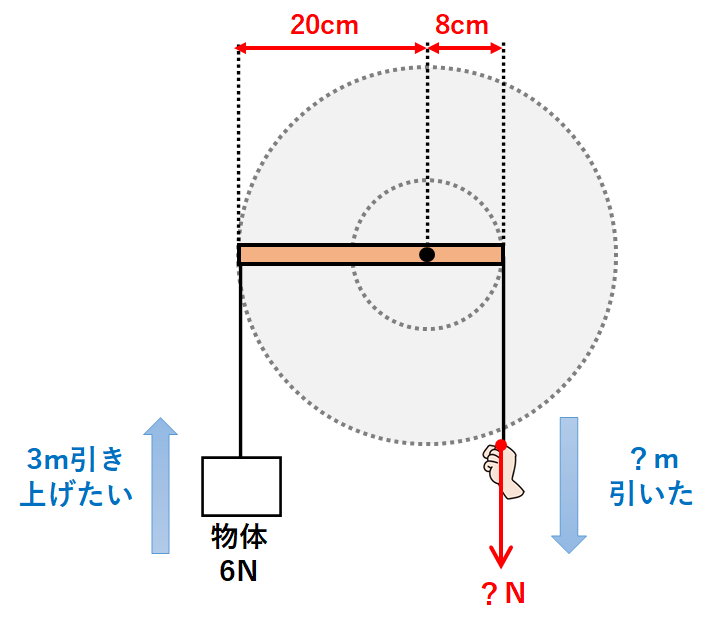
例題2
(答)
(1)
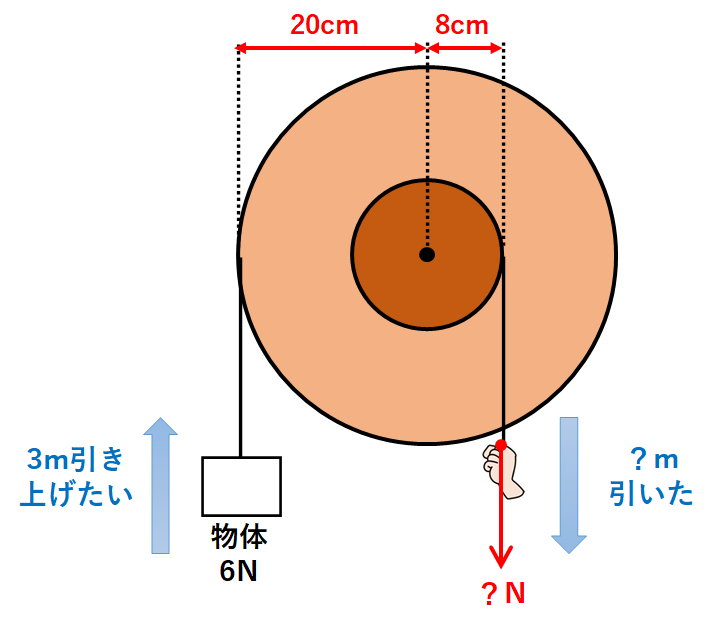
輪軸を↓のようなてこに置き換えてみましょう。
手が糸を引く力をx(N)として、力×うでの長さ=一定 であることを使います。
作用点の左側の力×うでの長さ=6N×20cm
作用点の右側の力×うでの長さ=x(N)×8cm
これらは等しいので
6N×20cm=x(N)×8cm
これを解いてx=15N
手が糸を引く力は15Nとわかります。
(2)
手が糸を引く距離をy(m)として、物体がされた仕事=手がした仕事 であることを使います。
物体がされた仕事=6N×3m=18J
手がした仕事=15N×y(m)=15y(J)
これらは等しいので
18=15y
これを解いてy=1.2m
手が糸を引く距離は1.2mとわかります。



コメント(承認された場合のみ表示されます)
こんにちは
わかりやすっかったです。
田中英二様
コメントありがとうございます。
お役に立てたなら幸いです。
またいつでもご覧ください。