2023年　奈良県公立入試問題　解説

このページでは2023年度（令和5年）の奈良県立入試一般選抜の問題を解説しています。(理科のみ)

問題・解答などはこちらから↓

https://www.pref.nara.jp/17661.htm

大問1の解説

(1)

れき岩・砂岩・泥岩は粒の大きい順に

れき岩→砂岩→泥岩

です。

貯留槽は「粒が大きい岩石からなる層」、遮へい層は「粒が小さい岩石からなる層」とあります。

そのような組み合わせになっているのはエです。

 

(2)

参考…【化学反応式のつくり方】

まず係数（大きな数字）を無視して化学反応式を書いてみましょう。

CH₄　＋　O₂　→　CO₂　＋　H₂O　・・・①

となります。（問題文より）

 

化学反応式では左辺と右辺で各原子の数が等しくなければなりません。

①の左辺では
C原子1個・H原子4個・O原子2個

①の右辺では
C原子1個・H原子2個・O原子2個＋1個＝3個

 

ここでH原子の数をそろえる（ともに4個にする）ために、右辺のH₂Oの前に係数2を付けましょう。

すると

CH₄　＋　O₂　→　CO₂　＋　2H₂O　・・・②

となり

②の左辺では
C原子1個・H原子4個・O原子2個

②の右辺では
C原子1×2＝2個・H原子2×2＝4個・O原子2＋1×2＝4個

となります。

 

あとは左辺のO₂の前に係数2を付けます。

CH₄　＋　2O₂　→　CO₂　＋　2H₂O　・・・②

こうすることで両辺ともに

C原子1個・H原子4個・O原子4個

となります。

大問2の解説

(1)

等圧線のルールでは・・・

①1000hPaが基準

②4hPaごとに実線が引かれる

③20hPaごとに太線が引かれる（940・960・980・1000・1020・1040・1060）

ことを知っておきましょう。

図1にも太線がありますが、これは940・960・980・1000・1020・1040・1060hPaのいずれかを表しています。

 

また点線の等圧線はとなりと2hPaちがう特別な等圧線です。（右上にある994や1010は点線の等圧線です）

Aはおよそ1010hPa、Bはおよそ1014hPa、Cはおよそ1006hPaです。

 

(2)

海陸風のでき方については→【海陸風】←を参考に。

 

(3)

冬はシベリア高気圧が発達します。

シベリア高気圧は大陸上にあるため乾燥しています。

日本の冬はシベリア高気圧から乾燥した冷たい北西の季節風が吹いています。

 

(5)①

空気中の水蒸気量は↓のように求めます。

$$空気中の水蒸気量=飽和水蒸気量×frac{湿度}{100}$$

したがって

$$空気中の水蒸気量=17.5g×frac{68%}{100}=11.9g$$

となります。

 

(5)③

寒冷前線の特徴は・・・

・通過すると気温が下がる

・通過すると風向が南寄りから北寄りに変わる

したがって18時から21時に寒冷前線が通過したとわかります。

 

大問3の解説

(1)

マグネシウムを硫酸銅水溶液（銅イオンがある）に加えることで赤色の固体（銅）ができています。

このことからマグネシウムの方が銅よりもイオンになりやすいことがわかります。

 

(3)

ダニエル電池では・・・

・亜鉛板の質量は減少します。（亜鉛板が亜鉛イオンとなり液中に溶けだすため）

・銅板の質量は増加します。（液中の銅イオンが電子を得て銅原子になるため）

・硫酸銅水溶液の青色がうすくなります。（青色のもとである銅イオンが銅原子へ変化するため）

・亜鉛イオンが硫酸亜鉛水溶液から硫酸銅水溶液側へ、硫酸イオンが硫酸銅水溶液から硫酸亜鉛水溶液側へ移動します。（両方の液の電気的なかたよりをなくすため）

 

大問4の解説

(1)

$$仕事(J)=力(N)×力の向きに動かした距離(m)$$

であるので

$$0.20N×0.12m=0.024J$$

となります。

 

(3)

この問いのような「木片の移動距離を求める」問題では

位置エネルギー：木片の移動距離＝一定

という関係を利用するとよいでしょう。

 

図3より、

質量10gの小球を4cmの高さに置くと木片が2cm移動する

ことがわかります。

 

このときの小球の位置エネルギーは

$$位置エネルギー=重さ(N)×高さ(m)=0.10N×0.04m=0.004J$$

ですので、0.004Jの位置エネルギーで木片を2cm移動させることができることになります。・・・①

 

またこの問いでは、

質量15gの小球をある高さに置くと木片が9cm移動

しています。

 

求める高さをx(m)とすると、その位置エネルギーは

$$位置エネルギー=重さ(N)×高さ(m)=0.15N×x(m)=0.15x(J)$$

 

0.15x(J)で木片が9cm移動しているので、①と合わせて

$$0.004J:2cm=0.15x(J):9cm$$

$$0.3x=0.036$$

$$x=0.12m$$

0.12m＝12cmとなります。

 

(4)

速さが等しいかどうかは運動エネルギーがどのような関係かを確認します。

図4・図5ともにスタート地点の高さや小球の質量は等しいため、図4の力学的エネルギー＝図5の力学的エネルギーです。

力学的エネルギーは保存されるので、F点における運動エネルギーは図4・図5で等しいので、小球の速さも図4・図5で等しいことになります。

 

(6)

点Pでも小球の速さは0になることはありません。すなわち運動エネルギーがいくらか存在することになります。

A地点の位置エネルギーよりP地点の位置エネルギーの方が、存在する運動エネルギーの分だけ小さくなります。

↓の動画も参考に。

 

大問5の解説

(2)

大さじ一杯のしょうゆは15㎤。

その密度は1.2g/㎤とあるので

$$しょうゆの質量=体積×密度$$

$$=15×1.2=18g$$

しょうゆは18gあり、その中に食塩が2.5g含まれていたことになります。

 

したがって食塩の割合は

$$食塩の割合=frac{2.5g}{18g}×100=13.88・・・$$

$$≒14％$$

となります。

 

大問6の解説

(1)・(2)

タンポポ・・・被子植物→双子葉類→合弁花類

ホウセンカ・・・被子植物→双子葉類→離弁花類

ドクダミ・・・被子植物→双子葉類→離弁花類

※ドクダミは日当たりの悪いところに生育しています。

ゼニゴケ・・・胞子でふえる植物→コケ植物

イヌワラビ・・・胞子でふえる植物→シダ植物

 

(3)

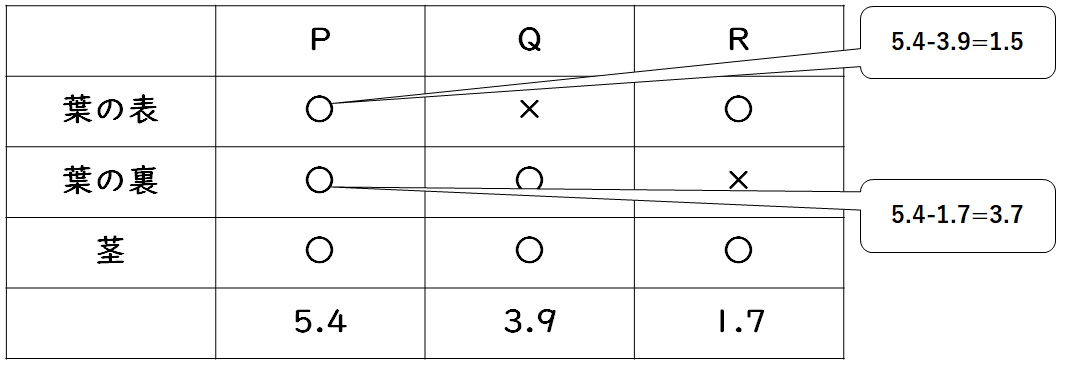
ホウセンカの蒸散する箇所を「葉の表」「葉の裏」「茎（葉以外）」に分けてみます。

そしてPQRの状況を表にまとめます。

蒸散できる部分（ワセリンをぬっていない部分）に○、蒸散できない部分（ワセリンをぬった部分）に×をつけます。（↓の図）

PとQでは水の減少量が5.4と3.9で、1.5の差があります。この差は葉の表の蒸散が原因です。

またPとRでは水の減少量が5.4と1.7で、3.7の差があります。この差は葉の裏の蒸散が原因です。

したがってホウセンカの葉の表と裏の蒸散量の合計は1.5＋3.7＝5.2gとなります。

参考→【蒸散の計算問題の考え方】

 

(4)

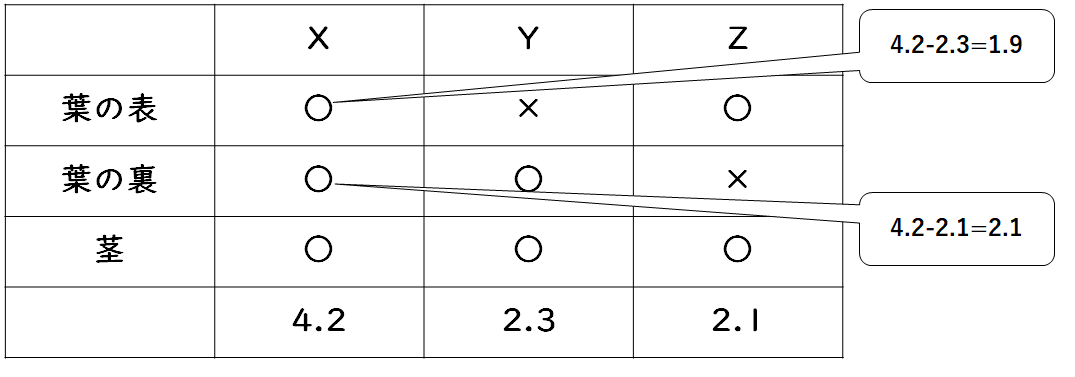
トウモロコシでも(3)同様に表にXYZの状況をまとめます。

X・Yよりトウモロコシの葉の表の蒸散量は1.9g、X・Zよりトウモロコシの葉の裏の蒸散量は2.1gです。

葉の表と葉の裏で蒸散量にそれほど差がありません。つまり水蒸気を放出する気孔の数にそれほどの差がないことを意味します。

一方で(3)よりホウセンカの葉の表の蒸散量は1.5g、葉の裏の蒸散量は3.7g。

ホウセンカの気孔の数は葉の表より裏の方が多いことがわかります。