このページでは2022年(令和4年)の大阪府立高校入試の理科の解説を掲載しています。
大問1の解説
(2)
生産者とは、光合成を行い、有機物(デンプンなどの栄養分)をつくり出す生き物です。
光合成を行う植物は生産者にあてはまります。
一方で消費者とは、他の生物を食べるなどによって、生産者のつくり出した有機物を直接または間接的に取り入れる生物です。
(3)①
1980年から1985年にかけて肉食動物Aは減少・草食動物Bは増加していることがわかります。
また問題文よりA・Bは食べる・食べられるの関係にあることもわかっています。
つまりAはBを食べているということ。
したがってAが減少したことにより、食べられる機会が少なくなったBが増加したとわかります。
(3)②
1985年から1987年にかけてBの数は減少しています。
Bの数が減少する原因として考えられるのは2つ。
①敵であるAが増加した。
②えさとしている植物が減少した。
グラフを見ると同時期Aの数は減少しています。つまり①が原因ではありません。
②のように、Bのえさである植物が減少した(Bが増加しすぎたことによって)ことが原因と考えられます。
(4)
外来種とは本来その地域に生息しない生物が、人間の手でその地域に持ち込まれたものを指します。
詳しくは→【在来生物と外来生物】←を参考に。
(5)
ア→二酸化炭素の性質です。
イ→酸素に刺激臭はありませんし、水にほとんど溶けません。あてはまるのは塩化水素です。
ウ→酸素は水にほとんど溶けません。また中性です。あてはまるのはアンモニアです。
エ→酸素の性質です。
(6)
分解者とは、消費者のうち落ち葉やふん・死がいなどから有機物を取り入れ無機物に分解する生物です。
土の中の小動物のほかに菌類(カビ・キノコのなかま)・細菌類などがいます。
(7)
炭素原子は有機物または無機物の形で自然界を循環しています。
物質の循環において有機物はデンプンなどの栄養分を指します。
また無機物は二酸化炭素を指します。
問題文「メダカは人工のエサのみを食べているものとする」とあるので、オオカナダモ(植物)からメダカに直接炭素原子に移動しているとは考えられません。
一方、メダカが呼吸によって放出した二酸化炭素は、オオカナダモの光合成によって移動している可能性があります。
大問2の解説
(3)
「Y先生の助言」から
水に加えられた熱量=水温上昇に利用された熱量+状態変化に利用された熱量
となることがわかります。
グラフの5分~6分で水温が上がりにくくなる=水温上昇に利用される熱量が少ない
ということなので
状態変化に利用された熱量が多くなることがわかります。
(4)
問題文に「水蒸気1Lで0.60g」とあるので、求める体積をx(L)とすると
1L:0.60g=x(L):15g
これを解いてx=25Lとなります。
(5)
状態変化では質量は変化しませんが、体積は変化します。
特に液体が気体になるときの体積の変化は大きいです。
(7)
物質がもつエネルギーを化学エネルギーといいます。
火力発電では化石燃料を燃焼することで、化学エネルギーを熱エネルギーに変換しています。
そうしてできた水蒸気を利用してタービンという器具を回転させます。
このように動いている器具がもつエネルギーが運動エネルギーです。
つまり火力発電では
化学エネルギー→熱エネルギー→運動エネルギー→電気エネルギー
と移り変わっています。
参考→【さまざまな発電方法】
大問3の解説
(1)
地球・月・太陽と並んだとき、太陽が月にかくされる現象を日食といいます。
月・地球・太陽と並んだとき、月に太陽からの光が当たらなくなる現象を月食といいます。
(2)
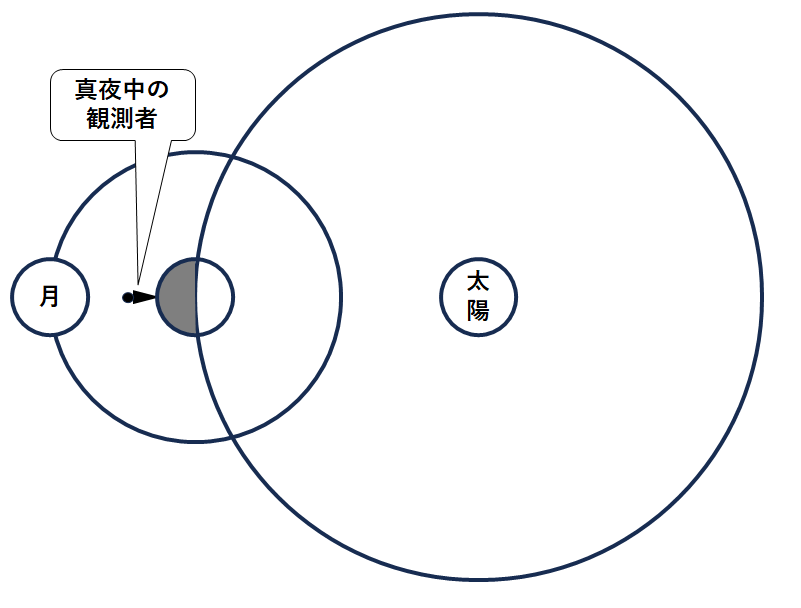
真夜中に月が見えているときの、観測者と月の位置関係は↓です。
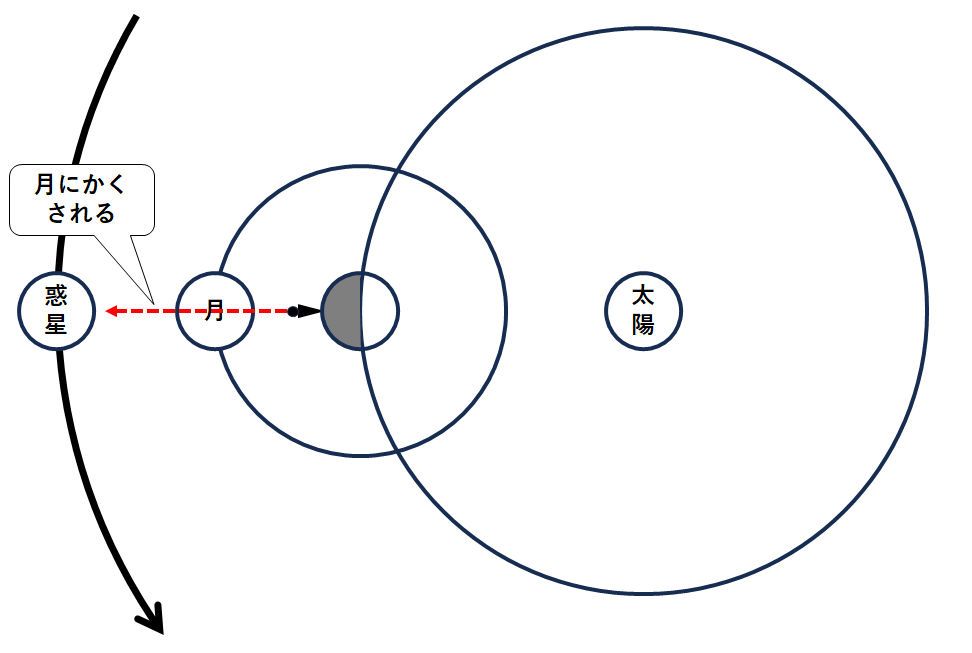
この月に惑星がかくされるとすると、↓のような軌道を公転している惑星が当てはまることになります。
つまり地球よりも太陽から遠いところを公転している惑星(外惑星)です。
選択肢では火星のみが当てはまります。
(3)
図Ⅰから11月8日の金星はよいの明星にあてはまることがわかります。
参考→【金星の満ち欠け】
(4)
【惑星や恒星が月にかくされる現象について調べたこと】の3つ目より
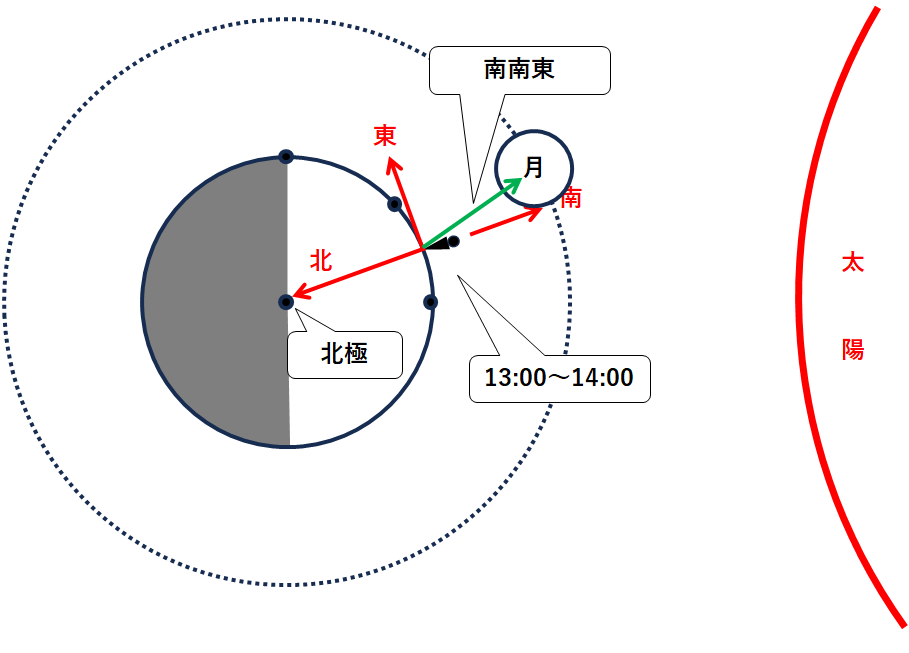
昼(13:44~14:26)の南南東の空に月が見えていることがわかります。
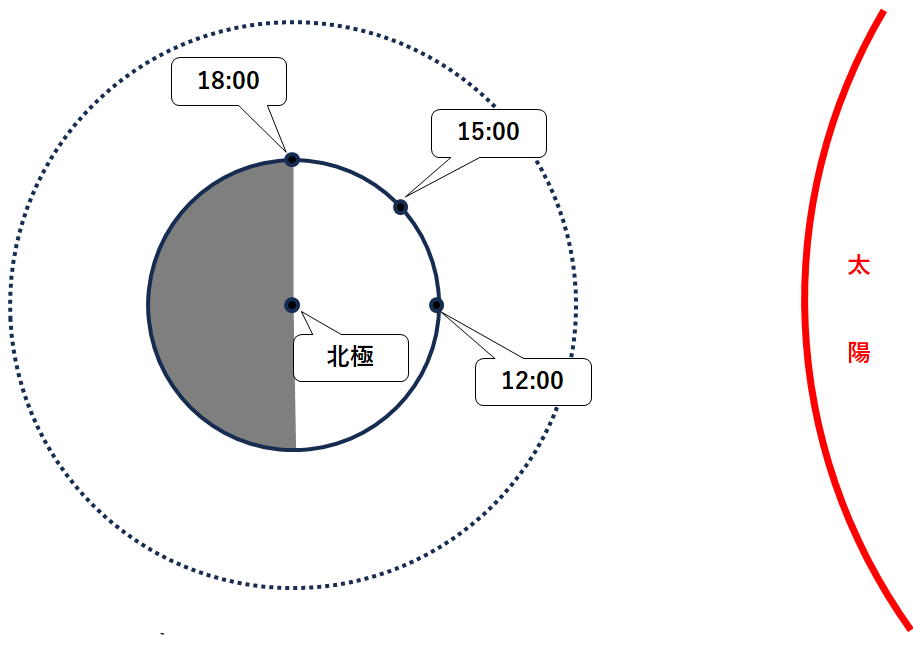
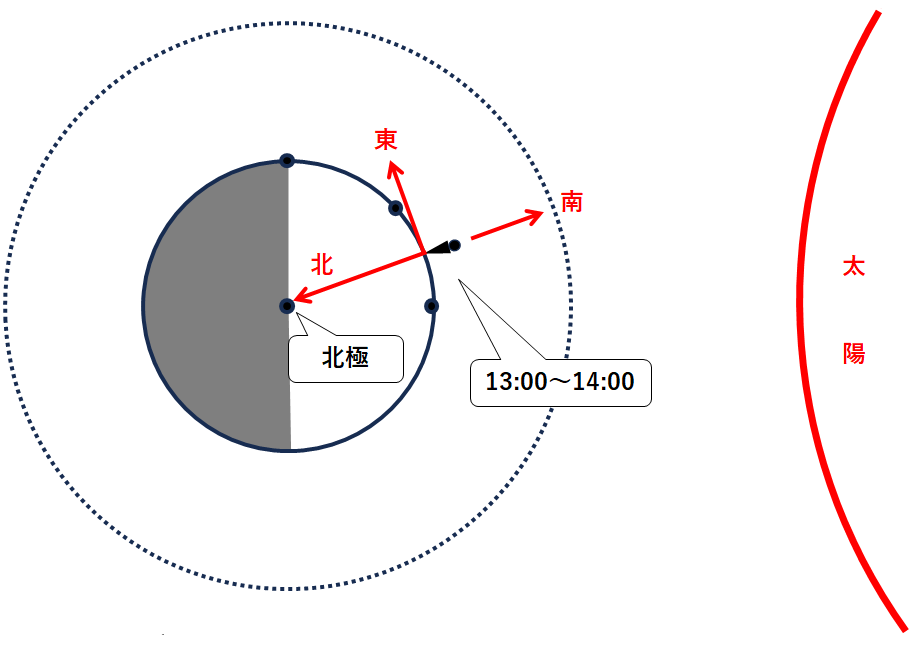
まず各時刻についてみてみましょう。(↓の図)
昼(13:44~14:26)の観測者を図示すると↓のようになります。
観測者から見て北極に向かう方向が北なので、南南東は↓のようになります。
この位置に月があるとすると、位置的に三日月がもっとも近い形だとわかります。
(7)
日周運動によりアンタレスは1時間で15°ずつ動きます。
年周運動によりアンタレスは1ヶ月で30°ずつ動きます。
E先生のセリフより、7月29日の20:00にアンタレスが南中することがわかっています。
この問いでは12:00にアンタレスが南中する月日を考えています。
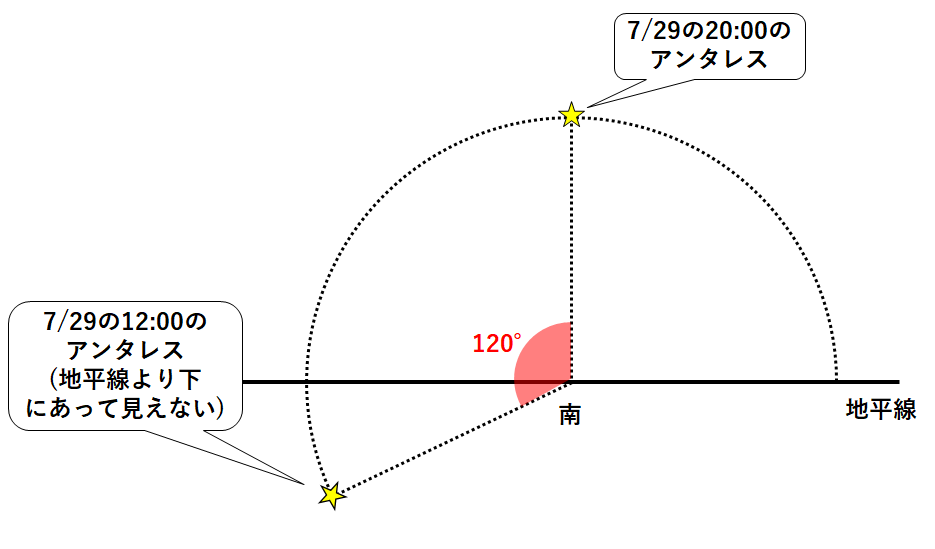
これは20:00の8時間前、日周運動より120°(=15°×8時間)だけ前の位置にアンタレスがあります。
7月29日の12:00にアンタレスは↓にあると考えられます。(日周運動より)
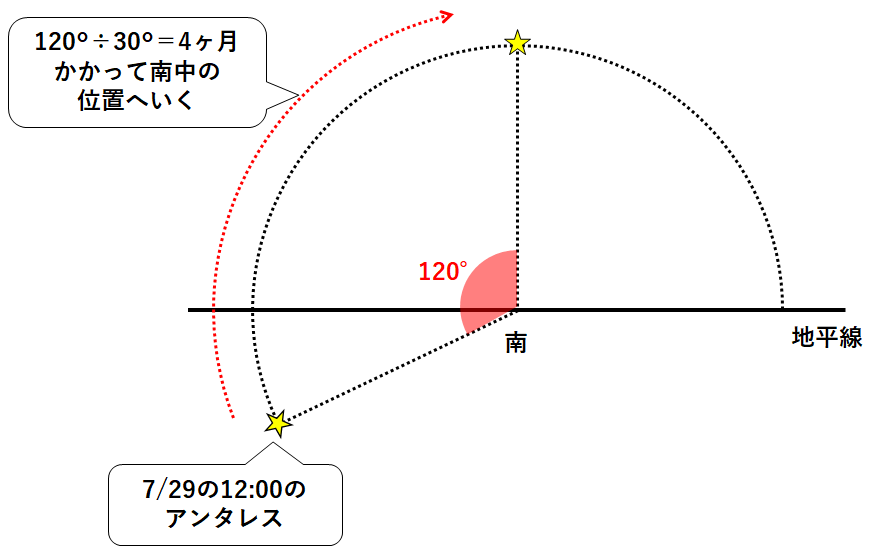
次に年周運動より、南中するまで4ヶ月後(=120°÷30°)の12時に南中することがわかります。(↓の図)
(別解)
星座の南中時刻は1ヶ月で2時間早くなります。(Gさんのセリフにもある)
7月29日の20:00に対して12:00に南中ということは、南中時刻が8時間早くなっています。
12:00に南中するのがxヶ月後とすると
1ヶ月:2時間=xヶ月:8時間
x=4ヶ月
とわかります。
(8)
3月19日の月は、朝6時に西の空に見えています。
明け方、西の空に見える月は満月です。
満月以降は満月→下弦の月→新月へと変化していきます。
したがって満月から欠けていき、東側(右側)が輝いていることがわかります。
参考→【月の満ち欠け】
大問4の解説
(1)
100gの物体にはたらく重力は1Nなので、250gの物体には2.5Nの重力がはたらきます。
(2)
何も力を加えていないときの長さは、グラフ図Ⅱの横軸「ばねに加えた力の大きさ」が0Nのときを見てみましょう。
(4)
図Ⅱよりこのばねは0.1Nで1cmのびることがわかります。
実験2の測定結果より、円柱Aが沈んでいないときのばねは31cmの長さ、完全に水中にあるときのばねの長さは19cmです。
水中に沈めることによりばねののびが12cm小さくなっています。
これは浮力が働き、重力の一部が打ち消されているからです。
浮力はばねののび12cm分なので、ばねが0.1Nで1cmのびることから考えると
0.1N:1cm=x(N):12cm
これを解いてx=1.2N、完全に水中にあるときの浮力は1.2Nとなります。
(5)
「しんかい6500」の動きをさまたげようとする力、とあるので、その力の向きは「しんかい6500」の動きとは逆向きです。
つまりアの向きであり、これは浮力の向きと同じ向きです。
(この力の正体は水から受ける抵抗力です)
(6)①
「円柱Bが浮かんで静止」とあるので、円柱Bにはたらく重力と浮力はつりあっています。
したがって浮力の大きさは1.0Nです。
(6)②
物体全体の重力=Bの重力+Cの重力×3 なので
物体全体の重力=1.0N+0.30N×3=1.9N
となります。
(6)③
C(体積20㎠×1.0㎝=20㎤)1つが完全に沈むとばねの長さは12㎝。
ばねが12cmのとき、ばねにはたらく力は0.1N。
C1つの重さは0.30Nなので、C1つが完全に沈んだときの浮力は0.20N。
図Ⅵの物体全体の体積は20㎠×(6.0㎝+1.0㎝×3)=180㎤。
浮力は沈んでいる部分の体積で決まります。(参考→【浮力について】)
C1つ(20㎤)が完全に沈んで0.20Nの浮力。
図Ⅵの物体全体180㎤が完全に沈んだときの浮力をx(N)とすると
20㎤:0.20N=180㎤:x(N)
これを解いてx=1.8Nとなります。

コメント(承認された場合のみ表示されます)